干湿循环泥质白云岩扩容特性及本构模型

2021-11-10蒋建国郭建强陈建行黄武峰卢雪峰杨前冬

土木工程与管理学报 2021年5期

蒋建国，郭建强，陈建行，黄武峰，卢雪峰，杨前冬

(贵州大学土木工程学院，贵州贵阳 550025)

软岩经干湿循环作用后力学性质软化规律的研究倍受国内外学者关注。实际的岩体工程常常遭受风化作用的影响，干湿循环是导致岩石风化的主要因素之一，吸水-风干循环作用对岩石的损伤有累积放大作用[1]，这严重影响了岩石工程的正常使用年限。国内外学者针对干湿循环对岩石力学性能的影响，从不同角度对岩石的损伤机制进行研究。邓华峰等[1]对三峡库区典型库岸边坡砂岩进行饱水-风干循环作用试验，探讨了孔隙水压力对岩样的影响；宋永军等[2]定义岩石的损伤度，并建立干湿循环次数与损伤度之间的函数关系；杜彬等[3]通过研究给出了干湿循环状态下红砂岩动态拉伸强度的计算公式；马芹永等[4]对不同干湿循环次数粉砂岩试件开展单轴压缩蠕变试验；王伟等[5]研究了大理岩在不同干湿循环作用下强度、变形和破坏形式等力学特性；江宁等[6]分析了矸石岩性、轴向应力及粒径级配对破碎矸石干湿循环长期承载变形特性及分形特征的影响；陈宾等[7]采用直剪试验和扫描电镜技术研究了对顺层红砂岩边坡稳定性起控制作用的软弱夹层在干湿循环条件下的力学特性；刘新荣等[8]通过试验获得砂岩在浸泡环境下抗剪强度随干湿循环次数的变化公式；Gökçeolu等[9]探讨了干湿循环次数、黏土岩矿物组分对于黏土岩耐久性的影响。刘帅等[10]研究了干湿循环对红砂岩煤矿井壁和巷道的力学特性及损伤劣化。

综上所述，当前对岩石干湿循环作用的研究成果多为岩石损伤机制和抗压强度方面，很少涉及岩石的扩容特性及本构模型。而岩石扩容直接关系到土木工程及油气储存的安全性问题，同时扩容现象也是地震发生的先前预兆[11～13]；本构模型可以较好描述岩石加载过程中的变形与强度特征。因此开展干湿循环作用下岩石的扩容特性及本构模型研究具有重要的现实意义。本文以贵阳地区某工地泥质白云岩为研究对象，通过常规三轴试验探讨干湿循环作用下泥质白云岩的扩容特性，并基于Mohr-Coulomb理论建立泥质白云岩的本构模型。

1 试验简介

试验在MTS岩石刚性试验机上进行，试验机系统由加载、测试和控制部分3部分组成。试验机的精度及性能均满足本次试验的要求。本试验为获取泥质白云岩在干湿循环作用下力学性质的变化规律而设计。岩样加工成Φ50 mm×100 mm的标准试件，其加工精度符合相关规范要求[14]。共设计3组试验，分别先进行干湿循环0次、干湿循环40次及干湿循环60次试验后进行三轴压缩试验。干湿循环试验的方法为：将制作好的岩样置于20±2 ℃的水中浸泡12 h，然后放入105 ℃的烘箱中烘干12 h，再自然冷却至室温。每个循环周期为24 h，如此反复。15个岩样均进行三轴压缩试验，围压为0，5，10，15，20 MPa。

2 岩石扩容特性

2.1 岩石的应力-体积应变曲线

岩石的应力-体积应变曲线分为4个阶段[12]：(1)压密阶段：体积应变曲线基本呈上凹行，以体积压缩变形为主；(2)弹性阶段：体积应变曲线近似直线，此阶段仍为体积压缩，但体积应变总量不大；(3)屈服阶段：此阶段开始出现塑性变形，体积变形由压缩转变为膨胀，其转折点称为扩容起始点，上限对应岩样的峰值强度，体积应变总量不大；(4)峰后软化段：此阶段岩石发生巨大的体积变形，肉眼可见岩块沿宏观断裂面滑动。

常规三轴试验中，体积应变εv按式(1)计算[13]。

εv=ε1+2ε3

(1)

式中：ε1为轴向应变；ε3为径向应变。准确记录每个状态点的轴向应变与径向应变，通过式(1)计算得出体积应变中的最大值点即为扩容起始点，对应的轴向偏应力即为岩石的扩容起始应力。

图1a，1b，1c分别为干湿循环0，40，60次时泥质白云岩的应力-体积应变曲线。岩样的体积压缩量随围压的增大而增大，体积由压缩转变为膨胀所需的时间越长，出现扩容的时间越长，显然围压可有效抑制岩样扩容的发生。最大体积应变随干湿循环次数呈非均匀性变化，围压0时，干湿循环0次为0.16%，循环40次为0.19%，循环60次为0.22%；围压5 MPa时，循环0次为0.16%，循环40次为0.21%，循环60次为0.16%；围压10 MPa时，循环0次为0.29%，循环40次为0.30%，循环60次为0.26%；围压20 MPa时，循环0次为0.49%，循环40次为0.20%，循环60次为0.44%。显然干湿循环作用对泥质白云岩扩容表现出非均匀的劣化特性。

2.2 扩容应力与峰值强度的关系

峰值强度σu为岩石单向或者三向受力状态所能承受的最大轴向压力，扩容应力σd为岩石体积由压缩转变为膨胀的拐点。扩容应力为峰值应力的60%～80%，该值目前主要由应力-体积应变曲线确定[14]。不同干湿循环次数扩容应力与峰值强度的比列并不一致，干湿循环0次时扩容应力为极限抗压强度的42%～85%，循环40次时为49%～76%，循环60次时为36%～90%。

将扩容应力与峰值应力的比值与围压进行拟合，发现应力比与围压具有很好的线性递增关系，图2为干湿循环0，40，60次时应力比与围压σ3的拟合曲线，图中N为循环次数，其拟合方程见式(2)～(4)，可见扩容应力与峰值应力的比值随围压的线性特性与干湿循环次数无关。

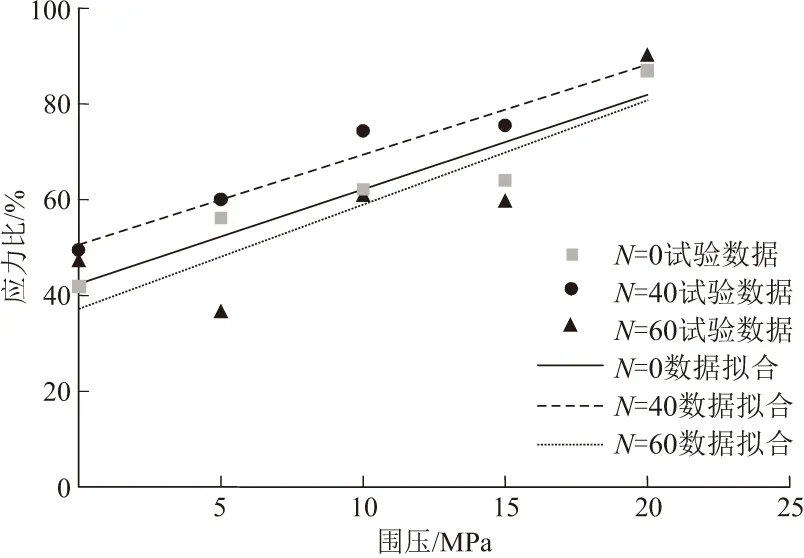
图2 应力比与围压的关系

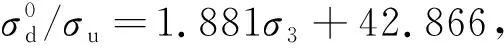
(2)

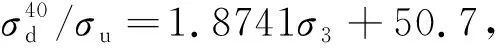
(3)

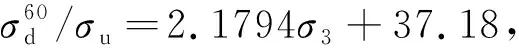
(4)

2.3 扩容应力与围压的关系

围压具有抑制岩石变形破坏的作用，且岩石的峰值强度与围压呈线性递增的关系[12]。将不同干湿循环作用下岩石的扩容应力与围压进行拟合，拟合结果如图3，拟合方程见式(5)～(7)。

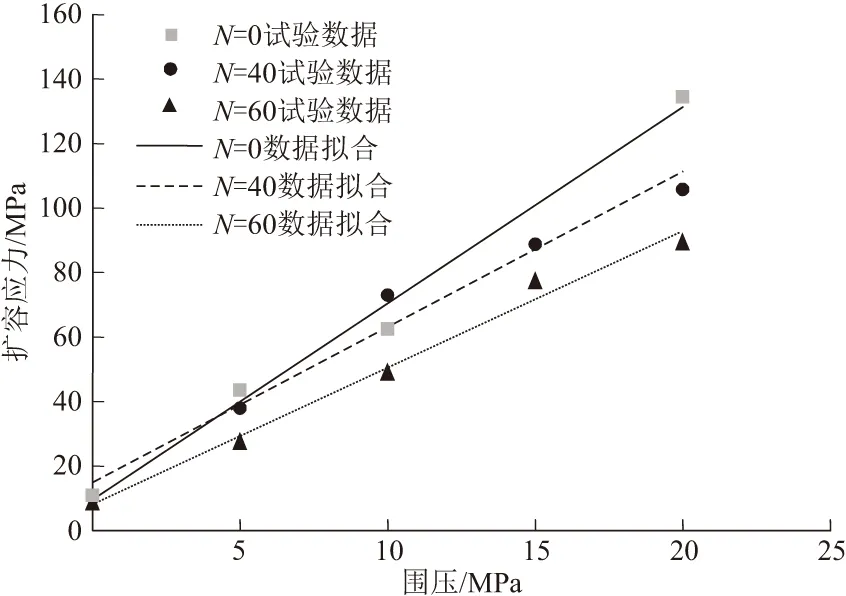
图3 扩容起始点应力与围压的关系

(5)

(6)

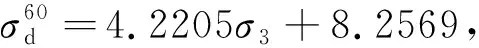
(7)

由图3及拟合方程可以看出，扩容应力随围压的增加而线性增加。拟合直线的斜率随着循环次数的增加而减小，说明干湿循环抑制了围压对σd的促进作用。另外，从0次循环到40次循环的过程中，其拟合方程斜率的增量为-1.2359，而从40至60次的过程中其斜率增量为-0.6117，说明干湿循环对扩容应力围压效应的抑制作用逐渐减弱，并近于稳定的趋势。

2.4 干湿循环对扩容应力的劣化规律

为了更好描述干湿循环状态下泥质白云岩的扩容特性，将干湿循环40次和循环60次相对于循环0次的总扩容应力增量T以及阶段扩容应力增量ΔT列于表1，其增量T及阶段增量ΔT按式(8)(9)计算。

T(i)=(σ0(i)-σN(i))/σ0(i)

(8)

ΔT(i)=Tn(i)-Tn-1(i)

(9)

式中：σ0为干湿循环0次的扩容应力值；σN为干湿循环N次时的扩容应力值；i为各级围压；n为相应于各级围压的阶段数。

由表1数据可以看出，干湿循环作用对泥质白云岩扩容应力的劣化效应是非均匀的，在干湿循环40次时，围压0，5，20 MPa的扩容应力分别下降了5.7%，13%，21.4%，表现为随围压增长的趋势。在干湿循环60次时，围压5，20 MPa的扩容应力分别下降了36.7%和33.5%，表现为高围压下，泥质白云岩的扩容应力下降量减少，说明在干湿循环60次时，围压可以一定程度地抑制泥质白云岩扩容应力的劣化。同时发现在低围压下的阶段应力增量随循环次数增长，而高围压下的阶段应力增量随循环次数下降。

表1 泥质白云岩扩容应力劣化分析

2.5 干湿循环对岩样的损伤分析

干湿循环作用是使岩石内部损伤逐渐放大的过程。岩石中存在着大量的孔隙、裂隙，水-岩作用损伤劣化在微细观上表现为岩石微观结构的变化，包括孔隙、裂隙、裂纹的聚集、扩展等，在宏观上表现为岩石力学性质的劣化[1～10]，如峰值应力、扩容应力降低。白云岩的岩石亚类为碳酸盐岩，泥质白云岩混有大量黏土矿物，未经干湿循环作用的泥质白云岩颗粒间接触良好，胶结物破坏前岩石的结构为近于连续状态[10]。与水接触后，产生胶结作用的黏土矿物遇水膨胀，充填了岩石存在的原生裂隙，由于黏土矿物分布的不均匀性，部分胶结物质膨胀过大将引起原生裂隙及次生裂隙的扩展。经过一次干湿循环过程后，岩石内部分矿物溶于水而流失，随着干湿循环次数的增多，岩样裂隙逐渐变大，数目增多，固体颗粒在水的作用下逐渐磨圆，从而导致泥质白云岩的峰值应力、扩容应力等强度参数下降。而在一定次数干湿循环作用后，岩石内部易与水反应的矿物成分(如黏土矿物)会流失殆尽，或剩余矿物含量不足以与水反应，此时岩石内部结构会达到一个新的动态平衡，力学性质会趋于稳定，这可解释随干湿循环作用的增加，扩容应力与围压的关系曲线趋于平行的现象。

3 力学参数的变化

鉴于本文岩石存在离散性，采用“分段线性平均斜率”[15]的方法对本次干湿循环下泥质白云岩的内摩擦角与粘结力进行求解，首先选取不同干湿循环次数下具备代表性的最大主应力与最小主应力值，在τ-σ坐标下作出相应的莫尔应力圆，如图4所示。分别确定各相邻莫尔圆的公切线与切点，则除了最小围压与最大围压所对应的莫尔圆之外，其余围压所对应的莫尔圆均有两条公共切线，将这两条公切线斜率的平均值作为此围压下莫尔圆的切线斜率。最小围压与最大围压对应的莫尔圆仅有一条公切线，直接取其斜率作为对应莫尔圆的切线斜率。此时每一个围压对应的莫尔圆均有一个斜率值，通过几何关系求取每一莫尔圆的切点坐标，并将切点坐标进行拟合，根据莫尔-库伦准则(见式(10))即可求得岩石的粘聚力c与内摩擦角φ。

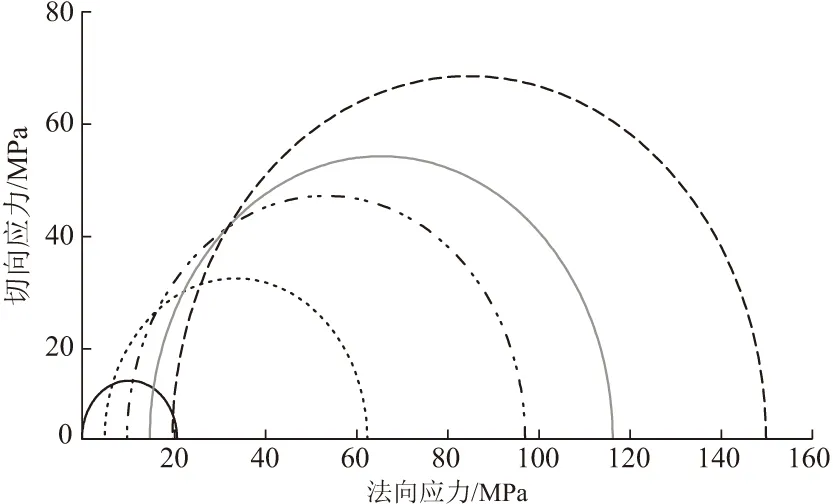
图4 扩容起始点计算的莫尔应力圆

τn=σntanφ+c

(10)

图5为干湿循环40次时泥质白云岩峰值点切向应力与法向应力的拟合关系，其拟合方程的斜率为1.0617，截距为5.2072，R2=0.9940。

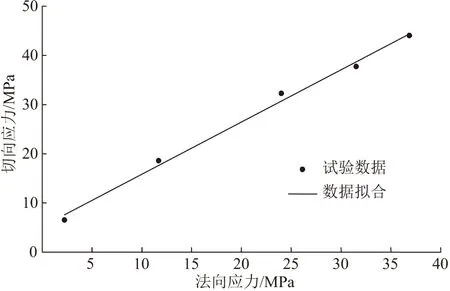
图5 切向应力与法向应力的关系曲线

将通过上述方法求取所得的各干湿循环次数下峰值点与扩容点的粘聚力与内摩擦角列于表2。

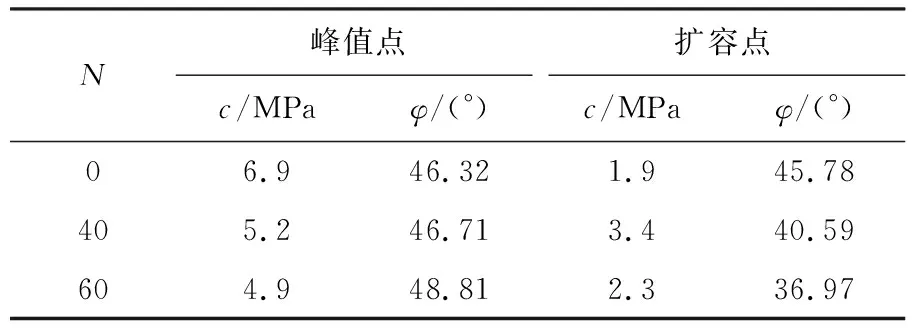
表2 峰值点与扩容点的力学参数

由表2可以看出，在干湿循环40次时，其峰值点摩擦角增加了0.8%，循环60次时增加了5.3%，变化幅度不大。而粘聚力在干湿循环40次时下降了25%，在循环60次时下降了29%，泥质白云岩的粘聚力受干湿循环的影响更为显著，随着干湿循环次数的增加而降低。内摩擦角随干湿循环次数的增加表现为上升的趋势，但其变化幅度比较平稳。而扩容点粘结力与内摩擦角的变化非常大，其粘聚力相对于循环0次时均有较大程度提高，循环40次时提高80%，循环60次时提升21%；摩擦角随循环次数的增加而下降，循环40次时下降11.3%，60次时下降19.2%，说明干湿循环作用对泥质白云岩扩容特性的影响大于对峰值强度特性的影响。

4 三轴压缩泥质白云岩本构模型

4.1 模型建立

本构模型可以很好地反应岩石的强度破坏特征。本文借鉴相关研究经验[16～18]，基于Lemaitre应变假说提出干湿循环作用下泥质白云岩的本构关系[19]，为相关的工程实例提供参考经验。

据Limaitre应变等价性假说得岩石损伤本构的基本关系为：

σ=σ*(1-D)=Cε(1-D)

(11)

式中：σ为应力矩阵；σ*为有效应力矩阵；C为材料的弹性矩阵；ε为应变矩阵；D为损伤变量。

岩石在外荷载作用下，其微元的破坏是随机的，定义损伤变量为岩石微元的破坏概率，实质就是岩石结构中已破坏微元的个数和总微元个数的比值，假定微元破坏概率的分布密度函数为P(x)，则损伤变量D可用式(12)表示。

(12)

式中：F为岩石的微元强度，F≥0，当F<0时，以F=0计算；x为微元强度的随机分布变量。本文假定F服从幂函数分布，概率密度函数用式(13)表示[20]。

(13)

式中：m和F0为幂函数的分布参数。

将式(13)代入式(12)得岩石的损伤变量D为：

D=(F/F0)m

(14)

岩石微元强度的确定是建立损伤本构方程的关键，M-C强度准则形式简单，且能很好描述岩石材料的强度特性[21]，因此本文将M-C强度准则作为岩石的微元强度，表达式为：

F=σ1-σ3tan2(45°+φ/2)

=2ctan(45°+φ/2)

(15)

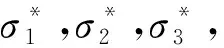
(16)

式中：E为岩石的弹性模量；ν为泊松比。

结合式(11)(16)得有效应力的计算式为：

(17)

将式(17)代入式(15)及得岩石微元强度的表达式为：

(18)

结合式(11)(14)(16)(18)即得岩石的损伤本构模型为：

(19)

4.2 参数m和F0的确定

目前岩石统计损伤本构模型参数的确定方法有拟合求解法和直接求解法[21]。拟合求解法即将式(20)进行适当变换，取不同围压对应的峰值强度作最小二乘拟合，通过拟合直线的斜率及截距计算相应的参数值。本文采用直接求解法确定本构模型的分布参数，模型在峰值点需具备一阶导数等于0且σ1=σu，结合此条件对式(19)求一阶偏导数得：

(20)

将峰值应力及峰值应变代入式(20)得：

(21)

式中：Fu为峰值点对应的微元强度；εu为峰值应变。

联立式(20)(21)即得模型的分布参数为：

(22)

(23)

4.3 模型验证

将不同干湿循环作用下围压5 MPa时泥质白云岩的应力-应变曲线与本构模型理论曲线作对比，结果如图6所示。峰值应力前曲线的拟合效果较好，峰后软化阶段吻合度欠佳，这可能与岩石本身的离散性有关。模型理论曲线总体上体现了泥质白云岩干湿循环作用下的应力应变关系，且曲线形态与岩石峰后软化特征相近，说明采用幂函数分布的统计损伤本构模型可以反映岩石峰后的力学行为，可为相关的工程实例提供参考作用。

图6 试验曲线与理论曲线的比较

鉴于本文试样的离散性较大，引用文献[22]的数据与本文模型进行对比。根据文献[23]资料，有E=90 GPa，ν=0.25，φ=31.3°，取围压为6.9 MPa的数据计算。结果如图7，从曲线的吻合度来看，本模型能较好地模拟岩石三轴压缩的应力-应变关系，尤其是在岩石破坏之前，进一步说明了本文模型的合理性。