灵活转化 巧解梯形

西北大学附属中学 曹建联

在初中数学教学过程中，不仅要教会学生熟记概念、套用公式、做对题目，而且要引导学生准确理解数学概念，发展学生的数学思维，培养数学思想方法。在不同版本的初中数学教材中，多个章节内容都渗透了最基本的数学思想方法，而转化思想在数学学习过程中可以说是贯穿始终，每每学习新知识的时候，通常采用化未知为已知、化复杂为简单、化抽象为具体、化陌生为熟悉的思维方式。转化思想会让学生在探寻问题的相互联系中，找到联系的关键点，获得解决问题的突破口，锻炼数学思维方式，提高学生的数学思维品质。在初中数学教材的多个章节中，多处都应用到了转化思想，本文就着重探讨转化思想在解决梯形问题中的应用。

作为特殊四边形的梯形，是初中阶段几何部分学习的重要内容，解决梯形问题对于学生来说既有似曾相识的感觉，又有无从下手的困惑，因此，在教学过程中，引导学生将梯形转化为已经学习过的三角形或平行四边形就显得尤为重要，通过转化使问题得到简化，从而有利于学生解决问题。在教学中常用的转化方式有以下四种情形。

【情形一】当题目中出现底角的三角函数时，则需构造直角三角形，具体方法是通过作梯形的两条高，将问题转化为解直角三角形和矩形问题

例1：如图1，梯形ADFE中，EF//AD，AE=DF，若AD=10，EF=4，tanA=2，求梯形的面积。

分析：由tanA=2 容易联想到构造含∠A的直角三角形，过点E作EB⊥AD，过点F作FC⊥AD，此时将梯形转化为矩形和三角形，问题得到解决。

解题思路：

①证明四边形EBCF为矩形，得到BC=EF=4；②证明△ABE≌△DCF，得到AB=CD=3；

③在Rt △ABE中，由tanA=2，AB=3，可得BE=6；④由梯形面积公式可得梯形的面积为52。

【情形二】当题目中出现两底角互余时，则需将互余的两个角转化到一个三角形中，这时会形成一个直角三角形。

方法一：通过作一条腰的平行线，将互余的两个角转化到一个三角形中，利用直角三角形的相关知识使问题得以解决。

例2：如图2，梯形ABCD中，AB//CD，∠A＋∠B=90°，若AB=10，AD=4，DC=5，求梯形的面积。

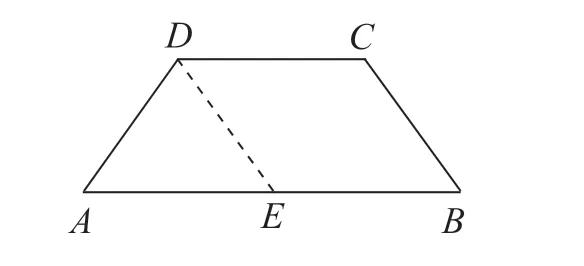
图2

分析：由条件∠A+∠B=90°会想到将∠A和∠B转化到一个三角形中，因此，过点D作DE//BC，将梯形转化为平行四边形和直角三角形。

解题思路：

①由DE//BC得∠DEA=∠B，同时证得四边形BCDE为平行四边形，BE=CD=5，由AB=10 可得AE=5；

②由∠A+∠B=90°得△ADE为直角三角形，由AE=5，AD=4 得出DE=3 ，△ADE的面积为6；

③因为平行四边形BCDE和△ADE等底同高，所以S四边形BCDE=2S△ADE，则S四边形BCDE=12；

④梯形的面积为6+12=18。

方法二：还可以通过将两腰延长，构造成直角三角形，使问题易于解决。

例3：如图3，在梯形ABCD中，AB//CD，∠B=30°，∠A=60°，CD=AD=6，计算AB的长度。

图3

分析：由题目中的已知条件∠A=60°，∠B=30°，可以联想到延长AD和BC，将会使问题转化为大家熟悉的直角三角形问题。当然，该问题也可通过作两条高解决。

解题思路：

①延长AD和BC交于点E，由∠A=60°，∠B=30°可得∠E=90°；

②由已知条件AB//CD，可得到两个含有30°的直角三角形，随后问题即可迎刃而解。

【情形三】当题目中的条件有对角线相互垂直时，则需将直角转化到对角线的一个端点，具体方法是通过平移梯形的一条腰，容易计算三角形的面积，间接得到梯形面积。

例4： 如 图4， 在 梯 形ABCD中，AD//BC，AB=CD， 对 角 线AC和BD相 互 垂 直， 若AD=4，BC=8，计算梯形ABCD的面积。

图4

分析：由题目中所给条件AC⊥BD，可将AC平移到DE，过点D作DE与AC平行，且与BC的延长线交于点E，得到△BDE为直角三角形，可通过计算三角形面积计算梯形面积。

解题思路：

①作DE//AC，由AC⊥BD得到DE⊥BD；

②又由AD//BC可证四边形ADEC为平行四边形，得DE=AC，CE=AD=4，由等腰梯形可知BD=AC，因此BD=DE，则△BDE为等腰直角三角形，BE=8+4=12；

③在等腰直角三角形BDE中，BE=12，S△BDE=36；

④由面积转化可得梯形ABCD的面积为36。

【情形四】当梯形为直角梯形时，可以通过延长两腰，使图形转化为直角三角形，从而使问题得到解决，

例5：如图5，在梯形ABCD中，AD//BC，∠B=90°，∠C=45°，AD=1，BC=5，E为AB的中点，EF//DC交BC于F点，求EF的长。

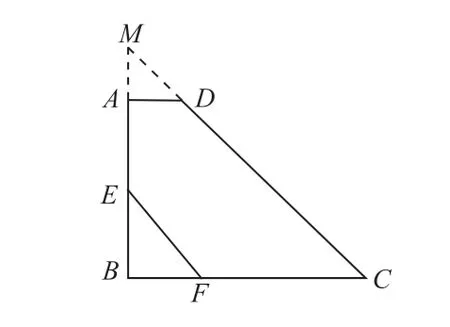
图5

分析：由题目中的条件∠B=90°，∠C=45°，可延长两腰得到一个等腰直角三角形，将梯形问题转化为熟知的等腰三角形问题。

解题思路：

①延长BA和CD交于点M，由∠B=90°，∠C=45°可得△MBC为等腰直角三角形，即BM=BC=5；

②由AD//BC得∠ADM=∠C=45°，∠MAD=∠B=90°，则△MAD为等腰直角三角形，即AM=AD=1；

③由BM=4，AM=1，可得AB=4，因为E为AB的中点，所以BE=2；

④因为EF//DC，所以∠BFE=∠C=45°，又因为∠B=90°，所以△BEF为等腰直角三角形，从而可计算EF的长度。

除了以上几种常见的情形外，还有其他的辅助线添加方法，将梯形问题进行转化。

例6：如图6，已知梯形ABCD中，AD//BC，EF是梯形中位线，△DEF的面积为4，则梯形ABCD的面积为多少？

图6

分析：由EF为梯形的中位线可知点E为AB的中点，可通过延长DE构造全等三角形，将梯形面积转化为三角形面积，从而使问题得到解决。

解题思路：

①延长DE和CB交于点M，因为AD//BC，所以∠M=∠ADE， ∠MBE=∠A，又因为BE=AE，所以△MBE≌△DAE，则梯形ABCD的面积等于△MCD的面积；

②因为△MBE≌△DAE，所以DE=ME，则EF为△MCD的中位线，可得△DEF与△DMC相似；

③因为△DEF的面积为4，所以△DMC的面积为16，所以梯形ABCD的面积为16。

总之，解决梯形问题的方法多种多样，不止这几种情形，在具体操作的过程中，根据题目所给已知条件，结合条件中边、角、对角线的不同特点，灵活应用添加辅助线、图形旋转或割补的方法进行图形转化，将梯形问题转化为较为简单、熟悉且容易解决的三角形问题或平行四边形问题，使问题分解、难度降低，从而达到解决问题的目的。当然，复杂的梯形问题可能会综合应用多种添加辅助线的方法，但其本质都是通过转化的思想化繁为简、化未知为已知，灵活迁移所学知识和方法解决新问题，创新思维方式，提高学生的数学素养和创新能力。