涡旋电磁波轨道角动量模态抗干扰性能分析

林屹峰 单明明 孔旭东 冯 强② 李 龙*②

①(西安电子科技大学超高速电路设计与电磁兼容教育部重点实验室 西安 710071)

②(人工智能与数字经济广东省实验室智能超材料中心 广州 510330)

1 引言

携带轨道角动量(Orbital Angular Momentum,OAM)的涡旋电磁波，其等相位波前特性与传统平面电磁波的等相位波前不同，并且其波束具有发散性[1]。由于相位因子项e(jℓφ)的作用[2]，涡旋电磁波具有螺旋形式的等相位波前，此处的ℓ表示涡旋电磁波所携带的OAM模态值大小，有时也称之为OAM模态阶数，ℓ可以取任意整数值，并且从理论上讲，不同阶OAM模态之间具有正交性。由此便构成了OAM模态的无穷维正交性，正是基于此特性OAM涡旋波束在无线通信以及雷达探测与成像领域表现出很大的研究潜力。对于无线通信而言，可以通过相互正交的OAM模态来传输多个数据流以提高信道利用率，增大通信系统的信息传输容量，相较于传统的通信技术具有更大的优势[3-7]。对于雷达探测与成像而言，可以将OAM模态作为一个新的信息维度，用于提高雷达回波信息的获取能力，以及探测目标的成像分辨率，尤其是对于雷达目标在方位角维度探测能力的提高具有重要作用[8-10]。

在经典的电磁理论中就有关于射频轨道角动量概念的论述，并且在随后也有相关的研究工作开展，只是大都处于理论阶段，还并未有相关的实验验证[11,12]。直到1992年，Allen等人[13,14]通过实验进一步研究显示拉盖尔-高斯波束具有完整的轨道角动量特性，并确定了轨道角动量和相位因子项e(jℓφ)之间的对应关系，这直接促进了轨道角动量研究领域的飞速发展。关于轨道角动量的研究一开始主要集中于光学领域[15]，而在2007年瑞典物理学家Thidé等人[16]通过均匀圆形阵列天线实现了射频轨道角动量的产生，产生了对应的涡旋电磁波束。自此，关于射频轨道角动量涡旋电磁波束的研究也进入了繁荣发展时期[12,17]，尤其是在无线通信和雷达探测与成像领域[10,18]，以及涉及涡旋电磁波产生与接收的关键天线技术[19,20]。

考虑到轨道角动量涡旋电磁波在实际的应用中，不同阶OAM模态之间的正交性会受到实际物理层实现以及应用环境的影响，所以对于OAM模态涡旋波束传输过程中的抗干扰性以及鲁棒性的研究也十分重要。早在2012年，Tamburini等人[21]所在的研究团队在他们的第1个关于OAM涡旋电磁波的通信实验中就提及了周围电磁环境对OAM涡旋波束传输的干扰问题，并且该研究团队随后从通信的角度，进一步分析了OAM涡旋电磁波在无线通信链路与系统中进行传输试验时的鲁棒性和抗干扰性能[22]。对于OAM在多径环境下的无线通信传输与干扰问题也有相关的研究工作，分别从理论建模、仿真以及实验等不同方面同现有的MIMO技术进行比较和分析[23-27]。需要指出的是，OAM涡旋电磁波作为一个具有坚实物理背景的研究领域，从物理领域即电磁的角度来看待和研究OAM涡旋波是很有必要的。

本文从涡旋电磁波与涡旋电磁场的角度切入，对OAM涡旋波束在传输过程中的抗干扰性能进行分析。本文主要研究内容如下：首先建立了平面相控阵列天线模型作为发射天线来产生具有不同OAM模态值的涡旋电磁波束，并引入喇叭天线作为干扰源，分别仿真和分析了在有无干扰源时对应OAM涡旋波束的空间电场分布变化情况，以及相应的OAM模态谱与OAM模态正交性的变化情况；进一步地，设计了相应的OAM涡旋波束接收天线阵列，构建起完整的OAM涡旋电磁波束收发射频链路模型，进行有关的OAM涡旋波束抗干扰性能分析；最后对所设计的OAM涡旋电磁波束产生与接收天线阵列进行加工，并以喇叭天线作为干扰源，对OAM涡旋波束的抗干扰性能进行了实验测试和对比分析。

2 涡旋电磁波发射天线阵列设计

本节主要设计了两个不同的涡旋电磁波发射天线阵列，分别产生OAM模态值为ℓ=+1 和ℓ=-2的涡旋电磁波束，并对相应的涡旋波束方向图以及在给定观察面内的涡旋电场分布进行了仿真计算，最后通过口径采样接收方法[28,29]，分析了无干扰源时对应的OAM模态谱纯度分布。

2.1 天线阵列设计与建模

图1-图3分别给出了本文所设计的OAM模态涡旋电磁波束发射天线单元及阵列模型。需要指出的是，考虑到后续加工和测试的便利性，本文在此处对天线阵列所需要的馈电网络也进行了集成一体化设计，并且为了简化馈电网络的设计，采用馈电中心位于天线结构中心的圆极化微带贴片单元作为阵列的阵元，天线单元结构图在图1中给出，具体参数见表1。

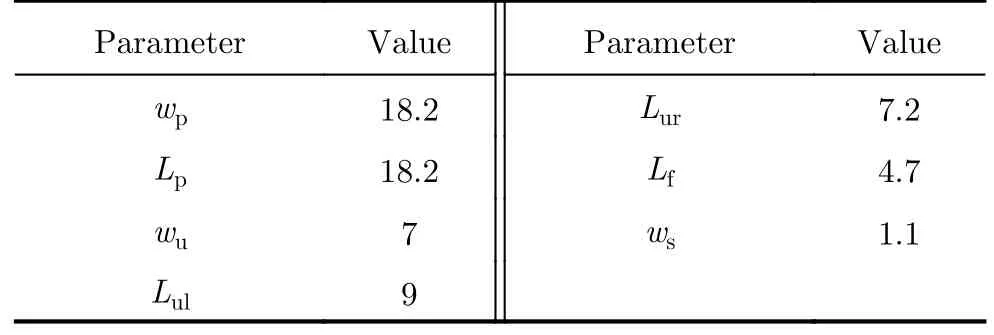
表1 4.25 GHz右旋圆极化天线单元尺寸参数(单位：mm)Tab.1 Size parameters 4.25 GHz of the designed right-handed circularly polarized antenna unit (Unit:mm)

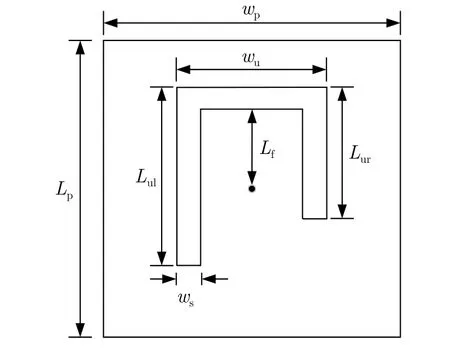
图1 右旋圆极化天线单元结构图Fig.1 Right-handed circularly polarized antenna unit structure diagram

本文的设计可以通过对微带贴片阵元以其馈电中心为旋转中心，旋转特定的角度来实现馈电网络所需要的相移，因此只需要对馈电网络进行等功分设计即可，从而实现馈电网络设计的简化。关于具体设计与实现过程，可通过有关参考文献获知[30-33]，此处不再赘述。两个天线阵列工作的中心频率均在4.25 GHz，所设计馈电网络均采用带状线叠层馈电设计，最终由天线阵列背面的馈电端口输入信号。图2和图3中所示的天线阵的阵列规模分别为8×8和10×10，其中模态值ℓ=+1的天线阵列尺寸为317.7 mm×317.7 mm，模态值ℓ=-2的天线阵列尺寸为390 mm×390 mm，天线阵元均采用半波长的间距，介质基板选取介电常数为2.65的F4B材料，天线层厚度为2 mm，叠层馈电网络各层厚度均为1.6 mm，阵列总厚度为5.2 mm。并且阵列设计均采取了阵列切角的方法来提高OAM涡旋波束效果[33]。而对于天线阵列的激励则可以通过式(1)计算得到。

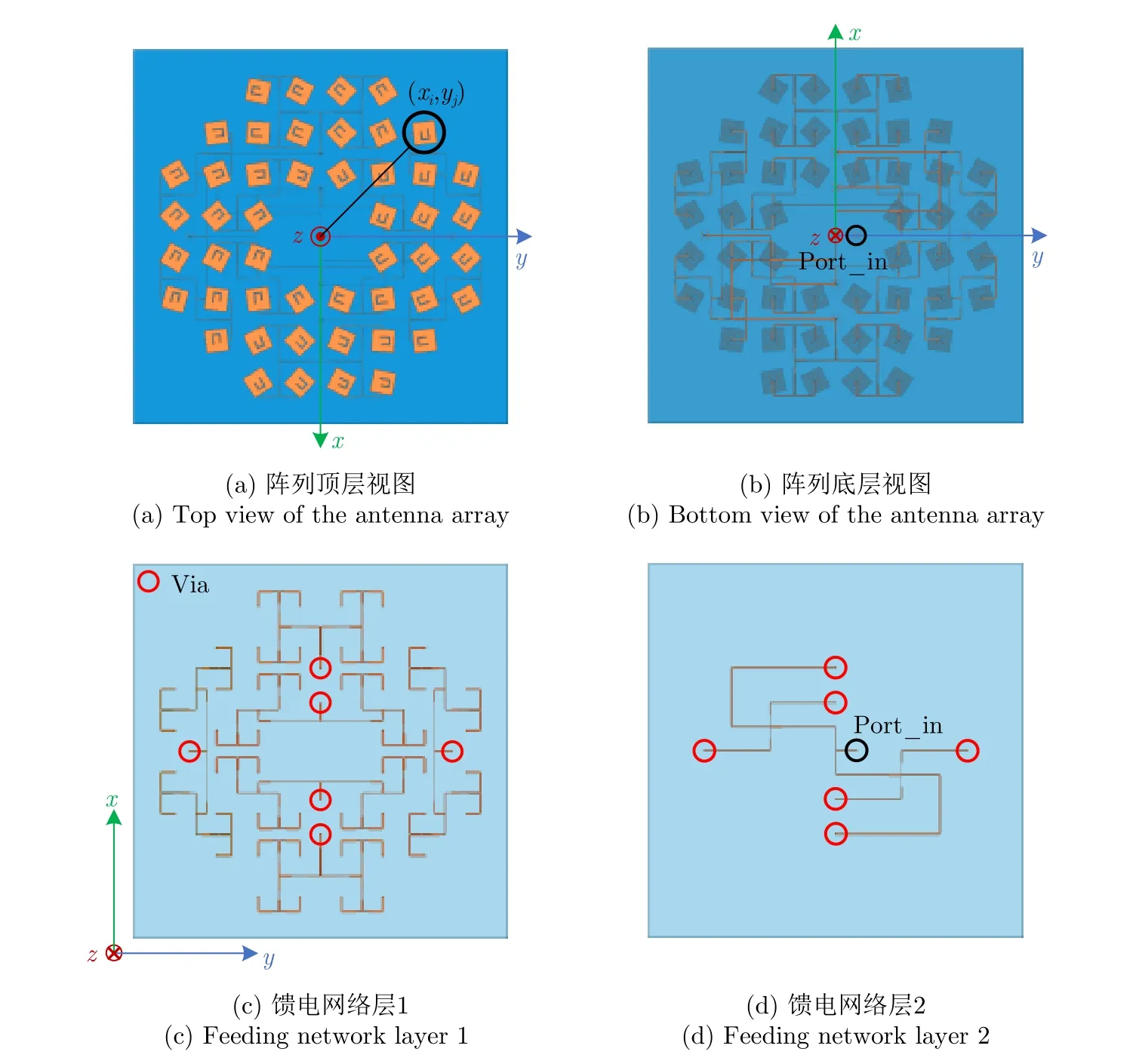
图2 涡旋电磁波发射天线阵列，用于产生OAM模态值ℓ=+1Fig.2 Designed antenna array for generating electromagnetic vortex beam with OAM modeℓ=+1

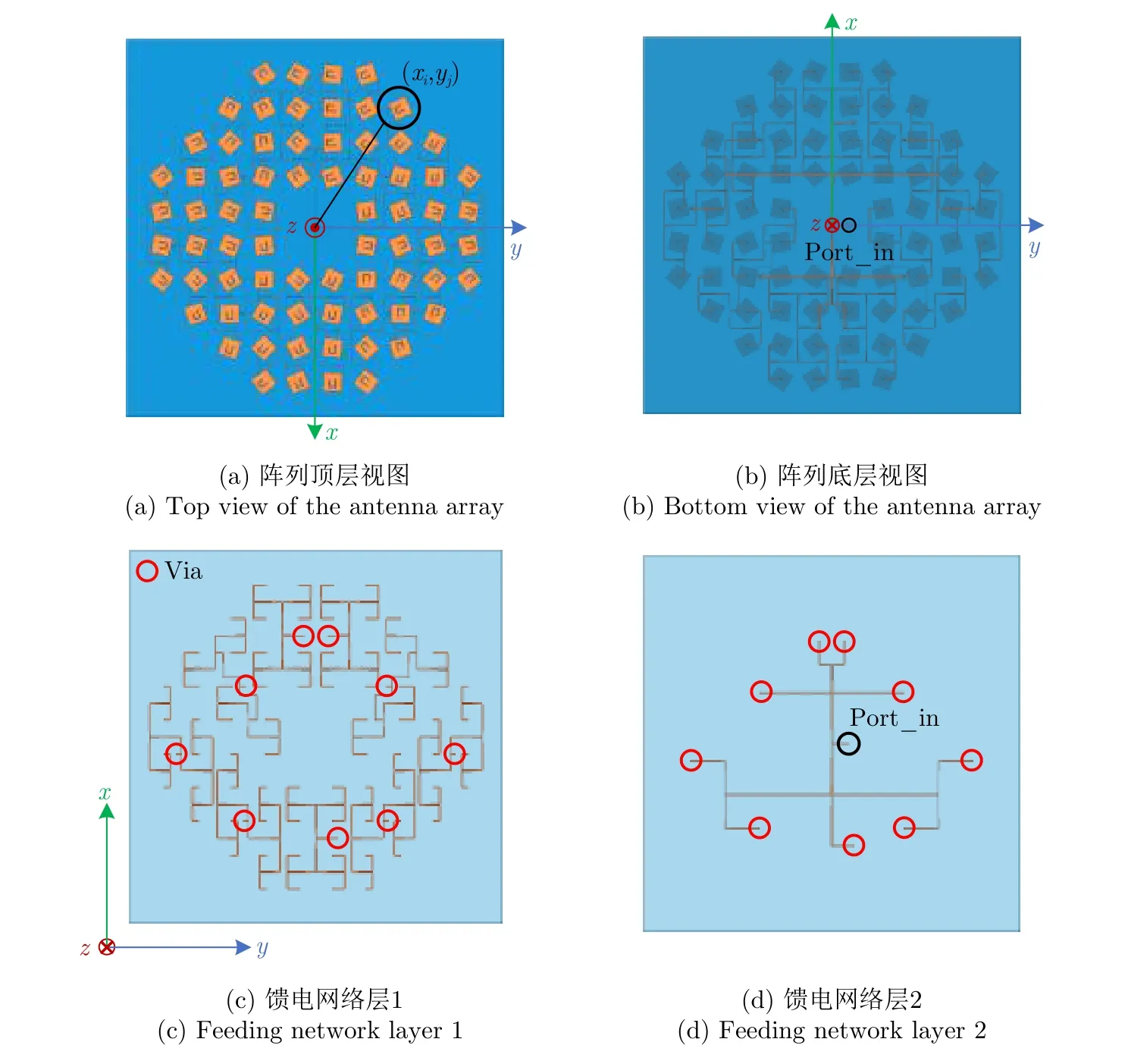
图3 涡旋电磁波发射天线阵列，用于产生OAM模态值ℓ=-2Fig.3 Designed antenna array for generating electromagnetic vortex beam with OAM modeℓ=-2

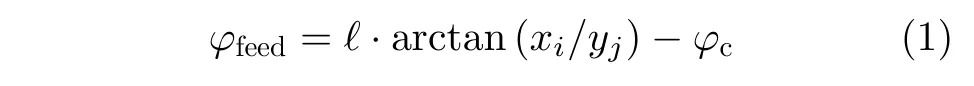
其中，ℓ表示相应的OAM模态值，(xi,yj)表示在给定坐标系下的阵元位置坐标，φc表示馈电网络的输入端口(即Port_in)到阵元之间由于馈电网络相位不一致性造成的补偿相位，φfeed则表示阵元所需要的激励相位，同时也对应阵元所需要进行旋转的角度。根据式(1)中计算得到的阵列单元激励相位设置，即可产生对应OAM模态值为ℓ的涡旋电磁波束。

2.2 仿真结果分析

将2.1小节中构建好的天线阵列模型在电磁仿真软件HFSS(High Frequency Structure Simulator)中进行全波仿真，可以分别得到的OAM模态值为+1和-2的涡旋电磁波束的3D方向图和2D方向图，如图4所示。进一步地，通过在距离天线阵列1.5 m处设立1 m×1 m大小的近场观察平面，可以仿真计算得到相应观察面内涡旋场的电场幅度分布与电场相位分布，然后再通过涡旋电磁波的口径采样接收方法即可计算出对应的OAM模态纯度分布。需要指出的是，在本文中不特别指出的情况下，所采用的口径采样接收方法均为均匀采样。

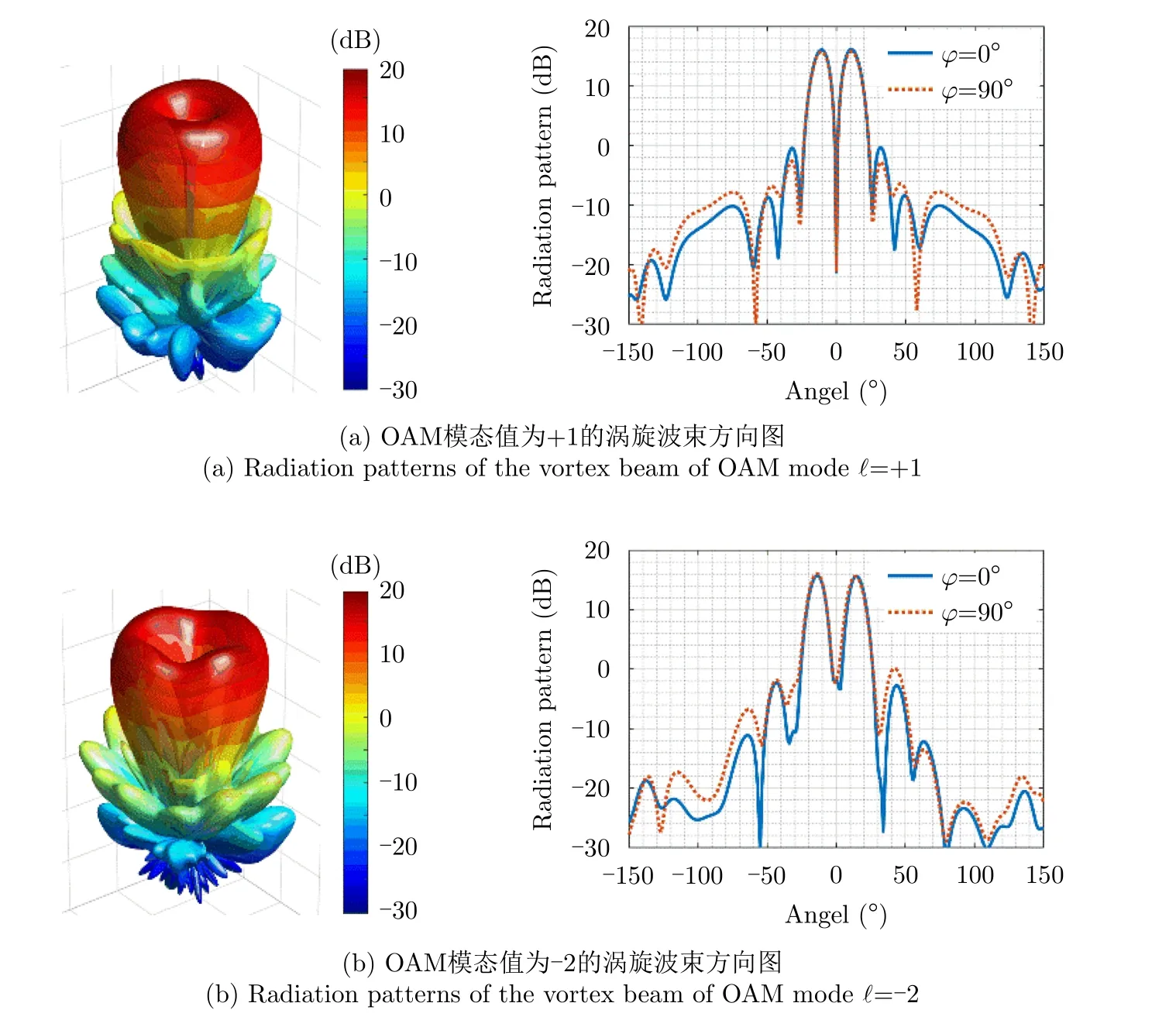
图4 天线阵列产生涡旋电磁波的3D及2D方向图Fig.4 Generated vortex beams’ 3D radiation pattern and 2D radiation pattern through the designed antenna array

图5给出了在场观察面内基本的涡旋波采样接收设置和对应仿真得到的涡旋电场分布结果。通过在场观察面内建立采样接收圆周进行OAM模态采样接收分析，其中r表示对应采样圆周的半径，即采样接收半径。在这里我们计算所用到的采样点数均为12个采样点。然后对位于采样接收圆周上采样点位置处的采样数据进行DFT(Discrete Fourier Transform)计算，并采用归一化的表示方法即可得到对应的OAM模态纯度分布[28,29]。式(2)即为本文中关于OAM模态纯度的定义。

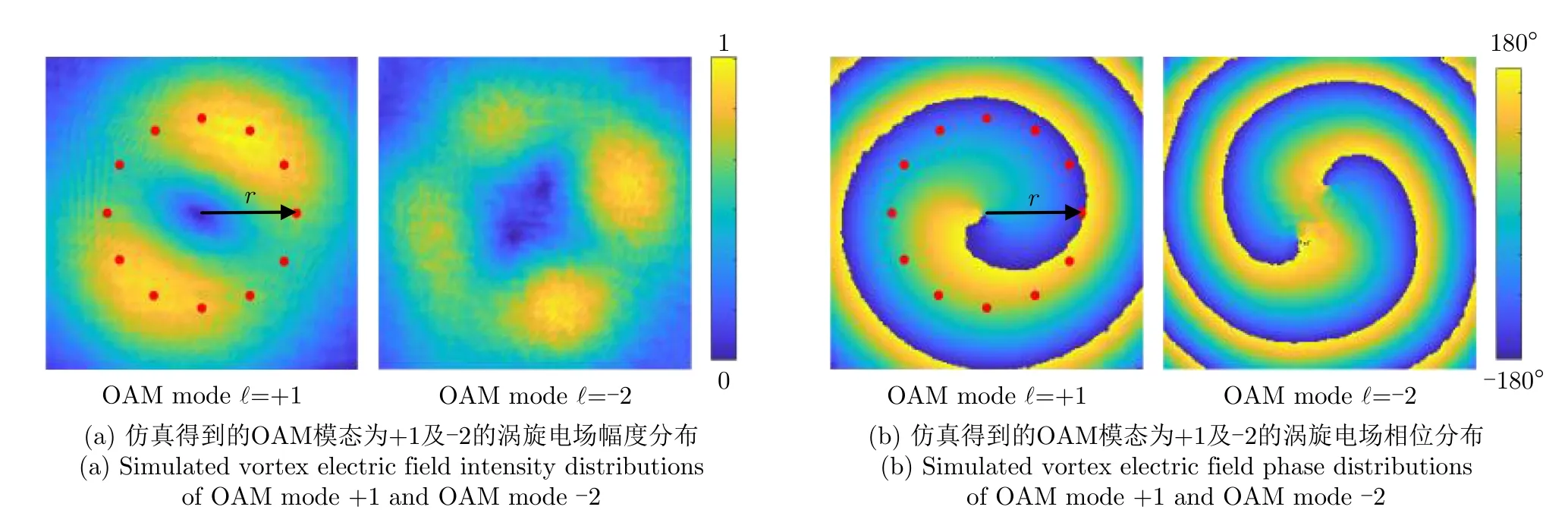
图5 在观察面上由天线阵列仿真得到的涡旋电场幅度分布图与相位分布图Fig.5 Simulated vortex electric field intensity distributions and phase distributions of OAM mode +1 and OAM mode -2 in the observation plane through the design antenna array

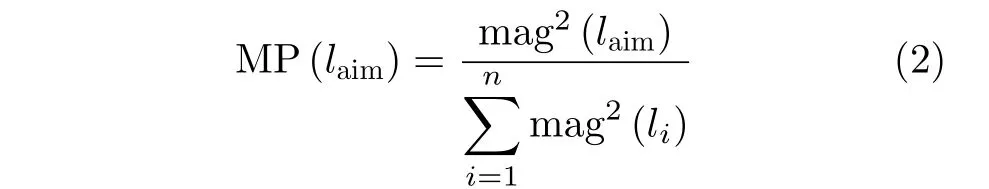
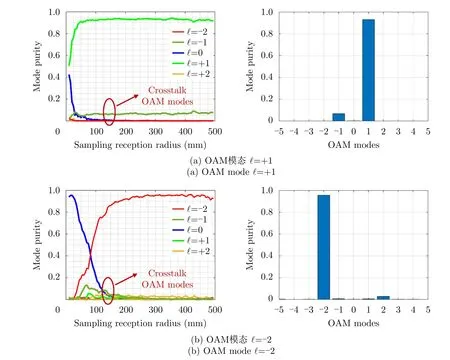
图6 OAM模态纯度随采样接收半径变化曲线图以及在固定采样接收半径为300 mm处的OAM模态纯度分布图Fig.6 Curves of the OAM mode purity versus the sampling reception radius,and the OAM mode purity spectrum at the fixed sampling reception radius of 300 mm

3 轨道角动量涡旋电磁波束抗干扰分析

本节主要对轨道角动量涡旋电磁波束抗干扰性能在较为理想的情况下进行仿真分析。所采用的仿真模型示意图如图7所示。涡旋电场观察面距离发射天线阵列的距离为1.5 m，场观察面的大小为1 m×1 m；以一个中心频率为4.25 GHz右旋圆极化喇叭作为干扰源，其距离观察面中心的距离同样为1.5 m，且干扰源喇叭的偏转角度可以在15°～45°范围内调节，本文主要选取了15°,30°,45°这3个具体的角度进行分析。需要指出的是，发射天线阵列和喇叭干扰源在天线激励端口具有相同的输入功率。

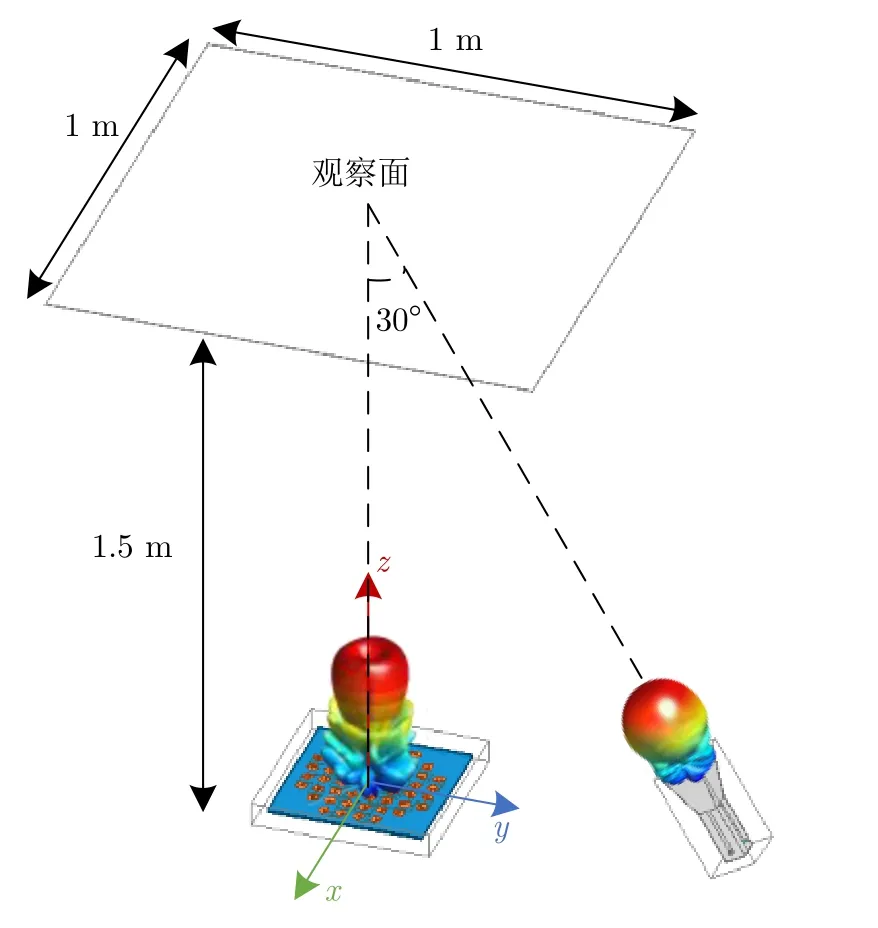
图7 轨道角动量涡旋电磁波束抗干扰分析仿真模型示意图Fig.7 Simulation model for electromagnetic vortex waves’ OAM mode ant-interference analysis

图8中给出的是在有喇叭干扰源时，场观察面内仿真计算得到的涡旋电场分布结果。从图8中可以看出，相比于第2节中无干扰源时的涡旋电场分布结果，在有干扰源照射时，涡旋电场的幅度分布和相位分布均呈现出了明显的干涉性条纹分布，这是由于喇叭干扰源在远场的辐射近似为平面波，当平面波与入射平面之间的入射角度增加时，由于电磁波的波程差不同会使平面上的相位分布呈周期性条纹变化，且条纹密度会随着入射倾角的增大而增大，当干扰源辐射场与产生的OAM模态涡旋场叠加后的相位相消使得条纹的致密程度增加。

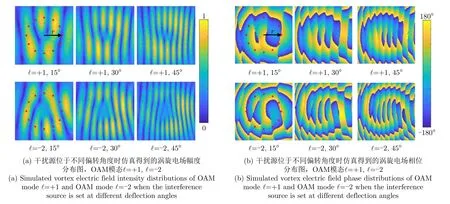
图8 干扰源位于不同偏转角度时仿真得到的涡旋电场幅度与相位分布变化图Fig.8 Simulated vortex electric field distributions when the interference source is set at different deflection angles

为了分析在有外部干扰源时的涡旋场信息是否还能够接收解调出完整的OAM模态信息，本文采用了和2.2小节中相同的全口径采样接收方法和参数设置，进行对比分析。图9分别给出了在外部干扰源位于不同照射角度时不同OAM模态的模态纯度随着采样接收半径变化的关系曲线图，以及在固定采样接收半径为300 mm处的OAM模态纯度谱分布图。由仿真计算结果可以看出，当存在外部干扰源时，用于传输的主OAM模态还是可以实现正常的接收解调的，但是相比于没有外部干扰源的情况，串扰OAM模态分量明显增加。

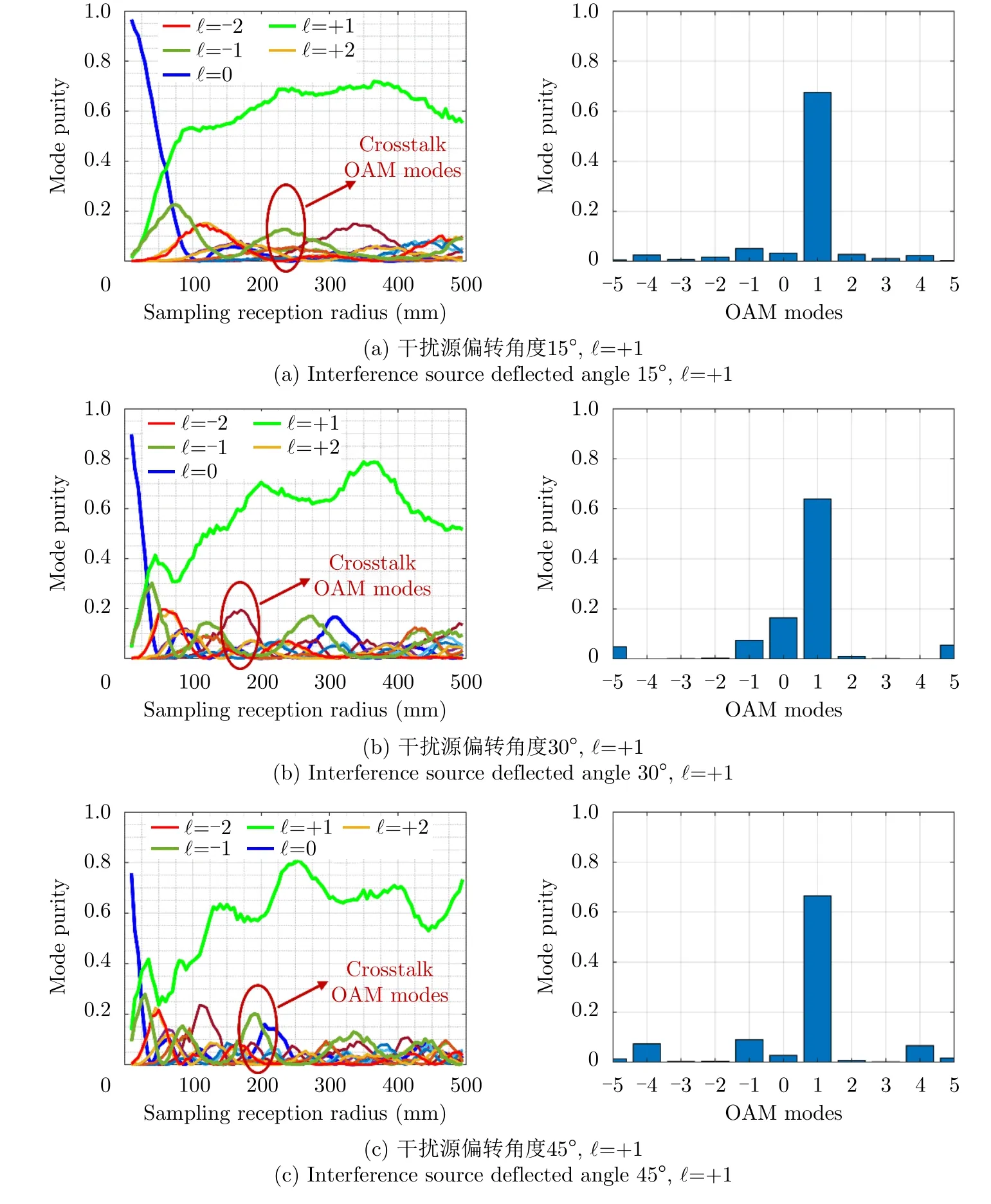
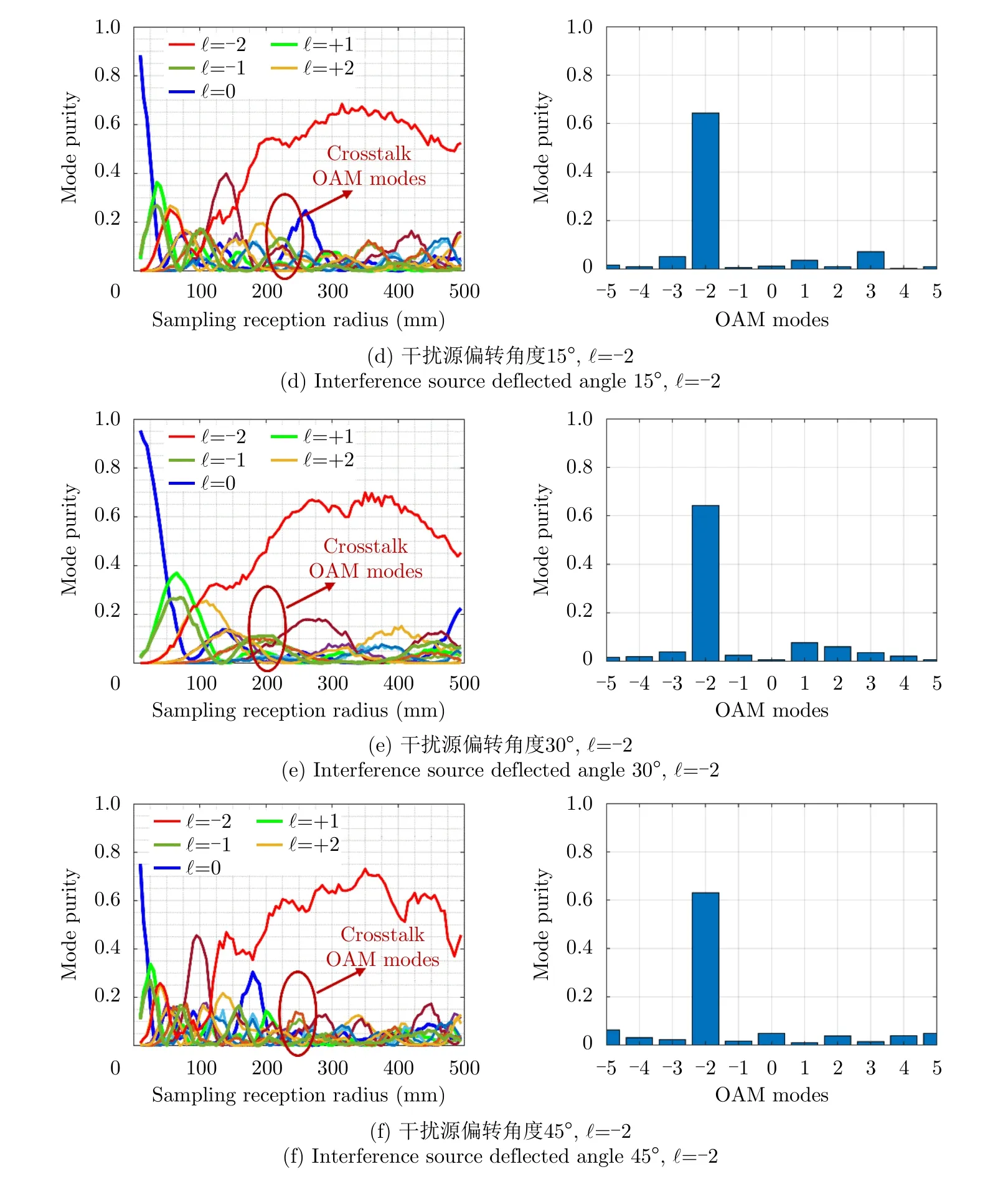
图9 外部干扰源位于不同照射角度时OAM模态纯度随着采样接收半径变化的关系曲线图及在固定采样接收半径为300 mm处的OAM模态纯度谱分布图Fig.9 Curves of the OAM mode purity versus the sampling reception radius when the interference source is located at different illumination angles,and the OAM mode purity spectrum at the fixed sampling reception radius of 300 mm

对于普通喇叭天线照射作为干扰源，它所产生的串扰OAM模态不仅有零阶OAM模态，还会产生其他的高阶串扰OAM模态。并且，随着干扰源照射角度的变化，对应引入的串扰OAM模态分布和大小也会发生相应的变化，即外部干扰源对OAM模态传输的影响也与对应干扰源所在的空间位置坐标相关。随着采样孔径大小的不同，对应模态的OAM谱纯度占比也随之变化，因此在空间中存在干扰源时，选取合适的采样孔径大小有益于OAM波束的解调。

4 轨道角动量涡旋波束射频收发链路的建模、仿真、测试及其抗干扰分析

本节首先建模仿真了用于不同OAM模态接收解调的接收天线阵列，进而搭建起了可用于轨道角动量涡旋波束射频收发链路分析的仿真模型。基于此，对OAM模态涡旋波束的传输性能以及抗干扰性能进行了分析，并完成了有关的实验测试和分析。

4.1 接收天线阵列设计

基于涡旋电磁波的口径采样接收理论和方法[28,34,35]，本文分别设计了全口径采样接收阵列天线和半口径采样接收阵列天线，分别用来实现对OAM模态值为+1和OAM模态值为-2的涡旋波束的接收解调。对于OAM模态值为-2的涡旋波束，从理论上来讲，通过半口径采样接收就可以保证OAM模态接收时的正交性[28,34]，出于文章篇幅的考虑，此处不再赘述。

图10所示为本文所设计的全口径采样接收均匀圆阵列天线与半口径采样接收均匀圆阵列天线的仿真模型。图10(a)中的全口径接收天线阵列由16个阵元构成，阵列基板材料与发射天线阵列一致，尺寸为300 mm×300 mm×3.6 mm，相邻阵元之间的沿着逆时针方向旋转的相位差为360°/16=22.5°，图10(b)中的半口径接收天线阵列由8个阵元构成，尺寸为300 mm×150 mm×3.6 mm，相邻阵元之间沿着逆时针方向旋转的相位差为360°×(-2)/16=-45°。同样地，对应单元的相位补偿也是通过旋转阵元来实现的。

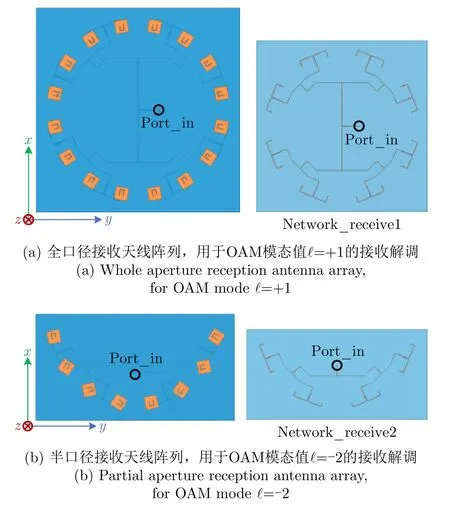
图10 不同OAM模态接收天线阵列模型Fig.10 Reception antenna array model for different OAM modes

4.2 轨道角动量涡旋波束射频收发链路建模与仿真

将距发射阵列1.5 m处的近场观察面替换为对应的全口径采样接收阵列及半口径采样接收阵列，就可对应建立起涡旋电磁波束发射与接收的射频链路模型。通过仿真分析干扰源分别偏转15°、30°及45°情况下，+1模态与-2模态的收发天线阵列及干扰源和接收天线阵列之间在4.25 GHz中心工作频率下的传输系数，来对OAM涡旋波束的传输性能与抗干扰性能进行分析，得到的仿真结果如表2所示。其中，“Match”表示对应OAM模态值的收发天线阵列之间的传输系数，“Interference”表示喇叭天线干扰源与对应OAM模态值的接收天线阵列之间的传输系数。

表2中的仿真结果表明，在天线的中心工作频率4.25 GHz处，干扰源的偏转角度在15°、30°以及45°这3种不同情况下，+1模态与-2模态轨道角动量涡旋波束射频收发链路的传输系数与干扰源间的隔离度均保持在10 dB以上，仿真结果表明轨道角动量涡旋电磁波具有较好的抗干扰能力。

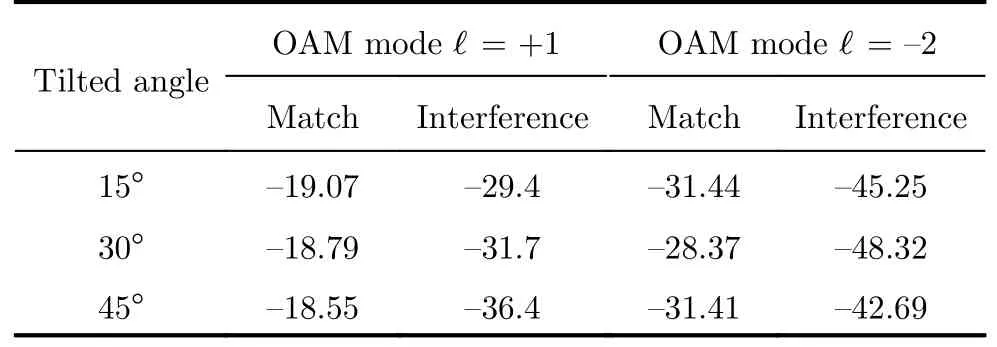
表2 不同OAM模态涡旋波束收发射频链路的传输系数仿真结果(单位：dB)Tab.2 Simulated transmission coefficients of vortex beams RF transceiver link under different OAM modes (Unit:dB)

4.3 轨道角动量涡旋波束收发射频链路抗干扰实验测试

图11所示为加工的轨道角动量涡旋波束收发天线阵列样机以及相应的测试环境，在收发链路及干扰源间使用矢量网络分析仪来测试射频链路收发端口之间的传输系数。调整接收阵列与发射阵列间的距离分别为1.5 m，同时干扰源的偏转角度分别调整为15°、30°以及45°，在不同情况下测试得到的OAM模态匹配传输系数以及干扰源与接收阵列之间传输系数结果如图12所示。需要说明的是，在图12中的“Match”和“Interference”的含义与表2中的含义相同。

图11 天线阵列实物及测试场景Fig.11 Antenna array prototype and the corresponding measurement environment

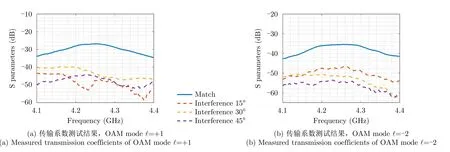
图12 不同OAM模态传输系数测试结果曲线图Fig.12 Measured transmission coefficients of different OAM modes

从图12中的测试结果可以看出，在4.2 GHz～4.3 GHz工作频段内，当喇叭天线干扰源具有不同的偏转角度时，干扰信号的传输系数也会有所不同，但是整体上对于当前场景本文所分析的OAM模态为+1及-2的射频收发链路来说，OAM模态收发天线阵列之间的传输系数相比于干扰源和接收阵列之间的传输系数，二者之间的隔离度均保持在10 dB以上，体现出较好的抗干扰效果。

5 总结

本文主要设计了两种不同OAM模态的涡旋电磁波束收发天线阵列，并建立了相应的射频收发链路仿真模型。通过电磁全波仿真的方法，主要从涡旋电磁波空间电磁场分布的角度以及OAM模态正交性保持的角度，对轨道角动量涡旋电磁波的传输性能以及在有干扰源情况下其抗干扰性能进行了仿真、测试与分析。影响涡旋电磁波传输的因素有很多，通过在有干扰源情况下对涡旋电磁波OAM模态谱以及OAM模态正交性进行分析，可以作为一个衡量维度对其抗干扰性能进行分析和把握。

本文所建立的涡旋电磁波射频收发链路模型较为简单，所分析的变量和参数也较少，更多地是旨在可以提供一种分析思路、方法和手段，为涡旋电磁波将来在无线通信系统和雷达系统中的应用提供一些可供参考的设计思路和分析基础。