High-resolution Sparse Self-calibration Imaging for Vortex Radar with Phase Error

QU Haiyou CHENG Di CHEN Chang CHEN Weidong

(School of Information Science and Technology,University of Science and Technology of China,Hefei 230027,China)

Abstract:The Orbital Angular Momentum (OAM)-based vortex radar has drawn increasing attention because of its potential for high-resolution imaging.The vortex radar high resolution imaging with limited OAM modes is commonly solved by sparse recovery,in which the prior knowledge of the imaging model needs to be known precisely.However,the inevitable phase error in the system results in imaging model mismatch and deteriorates the imaging performance considerably.To address this problem,the vortex radar imaging model with phase error is established for the first time in this work.Meanwhile,a two-step self-calibration imaging method for vortex radar is proposed to directly estimate the phase error.In the first step,a sparsity-driven algorithm is developed to promote sparsity and improve imaging performance.In the second step,a self-calibration operation is performed to directly compensate for the phase error.By alternately reconstructing the targets and estimating the phase error,the proposed method can reconstruct the target with high imaging quality and effectively compensate for the phase error.Simulation results demonstrate the advantages of the proposed method in enhancing the imaging quality and improving the phase error estimation performance.

Key words:Vortex radar imaging;Orbital Angular Momentum (OAM);Phase error;Self-calibration;Sparse recovery

1 Introduction

It is well known that Electro Magnetic (EM)wave carries angular momentum,wherein Spin Angular Momentum (SAM) is associated with polarization and Orbital Angular Momentum (OAM)is related to spatial distribution[1].Since the vortex light beam carrying OAM is discovered in 1992[2],the EM vortex wave has attracted increasing attention in the field of optical manipulation[3],wireless communication[4,5],radar imaging[6-11]and rotation Doppler detection[12,13]etc.Researches show that vortex EM waves theoretically can carry infinite numbers of OAM modes (topological charges) and different OAM modes have orthogonality[1,9].Moreover,the unique wave front of vortex EM wave shows the characteristic of angular diversity,which provides a new prospect for improving the radar imaging performance.

In 2013,Guoet al.[6]proposed the fundamental imaging model and principle of vortex radar firstly based on Uniform Circular Array (UCA),wherein the approximate Fourier duality relationship between OAM mode and azimuth is utilized to obtain the azimuth profile of the target,In addition,research demonstrates that the more OAM modes are utilized,the higher azimuth resolution can be obtained.Subsequently,Qin and Liu implement the pattern optimization and beamforming for vortex radar imaging in Refs.[14,15],and the 2D-FFT method was applied to image the target after beamforming.Moreover,the modelbased Power Spectrum Estimation (PSD) approaches were utilized to obtain high-resolution target image[9].For the FFT and PSD methods developed in Refs.[9,14] and Ref.[15],a sufficient number of OAM modes should be applied to achieve high imaging resolution.However,generating a sufficient number of OAM modes for UCA-based vortex radar is too expensive to implement,which seriously limits the improvement of resolution in practice.The inherent orthogonality of OAM modes enables the reconstruction of targets with limited measurements.Thus,to achieve high resolution imaging with limited OAM modes,the sparse recovery algorithms proposed in recent years were introduced to vortex radar imaging[16-18].The Orthogonal Matching Pursuit (OMP) method were applied to achieve high-resolution imaging for air targets[18].However,the target sparsity degree needs to be known in advance.Moreover,the Sparse Bayesian Learning (SBL) was introduced to reconstruct the targets for vortex radar imaging[16],and achieved excellent imaging performance.And a two-dimensional Non-Convex Augmented Lagrangian Method[17](2D-NCALM) was proposed to achieve sparse image and reduce computational complexity.However,the above sparse recovery methods are sensitive for model error,and the imaging models need to be known precisely.

Although the above mentioned works contribute a lot to the high resolution imaging of vortex radar application,most of the existing works are carried out under ideal conditions,which may not be consistent with the realistic situations.As a multi-channel radar technology,the phase error caused by channel inconsistency inevitably exists in UCA-based vortex radar system in the realistic world,which results in imaging model mismatch and degrades the imaging performance considerably.

Phase error has been intensely studied in multi-static radar systems[19-21].In MIMO radar imaging,the signals of different channels are separate before imaging process,and the phase error caused by channel inconsistency is taken as a multiplicative diagonal matrix in these self-calibration methods[22,23].However,for the case of vortex radar,the problem is quite different because the signals of multiple channels need to be combined into an OAM mode signal,and the echoes of different channels are correlative in the imaging process.This makes the compensation for phase error in vortex radar much more different and difficult.Furthermore,according to our best knowledge,there are few literatures provide effective solutions to vortex radar imaging with phase error problem,especially under limited OAM modes,which brings great obstacles to the practical application of vortex radar high resolution imaging.

Therefore,the aim of this work is to theoretically analyze and compensate phase error caused by channel inconsistency in the vortex radar imaging system under limited OAM modes.The vortex radar imaging model with phase error is established firstly,and a two-step self-calibration method for vortex radar with phase error is proposed which takes alternate steps to reconstruct the target image and estimate the phase error.In the proposed self-calibration method,the reconstruction of the target image and the estimation of the phase error are involved with each other.Thus the estimation accuracy of the phase error will have great impact on the results of the target image reconstruction,and vice versa.So the image recovery algorithm should be elaborately designed.

Recent developments in radar imaging[24-26]demonstrate that statistical structure sparsity provides further performance benefited by imposing structure sparsity as a statistical prior on the scattering coefficient of the targets.Hence,a new spike-and-slab-based structure sparse prior is proposed in the image reconstruction to promote structure sparsity for the target image reconstruction.

The main contributions of this work are twofold:(1) this work establishes a vortex radar imaging model with phase error for the first time;and(2) a two-step self-calibration imaging method for vortex radar is proposed.At the first step,a sparsity driven algorithm is proposed which utilizes a novel structural sparse prior to promote sparsity and improves the imaging performance.Meanwhile the posterior of the target image and latent variables are updated by variational Bayesian theory.At the second step,the phase error is estimated accurately by Maximum Likelihood Estimation (MLE),and a self-calibration operation is proposed to directly compensate the phase error.By alternately reconstructing the targets and estimating the phase error,the proposed method can reconstruct the target with high imaging quality and effectively compensate the phase error.Simulation results illustrate the effectiveness of the proposed method in the presence of phase error and the robustness to noise,meanwhile the proposed method has excellent adaptability to image targets with different sparsity and structure distribution characteristics.

The remainder of this article is outlined as follows.The imaging model of vortex radar with phase error is established and the imaging performance influence of phase error is analyzed in Section 2.In Section 3,the structural sparse prior for vortex radar imaging is proposed firstly,and the proposed self-calibration algorithm is given.Simulations are taken to verify the effectiveness of the proposed method in Section 4.Conclusions are drawn in Section 5.

2 Problem Formulation

In this section,we will deduce and establish the vortex radar imaging echo model with phase error.At the same time,the imaging performance influence of phase error is analyzed from the perspective of Point Spread Function (PSF).

2.1 Vortex radar imaging model with phase error

For radar imaging applications,the vortex radar system can be realized by a phased UCA[7,27],as illustrated in Fig.1.Nantenna elements are placed at the ring with equal intervals,a phase shift of eiαϕn=eiα2πn/Nis added to thenthelement.The phase difference between two adjacent elements is Δϕ=2απ/N,whereαis the OAM mode number (topological charge).In order to generate a vortex electromagnetic wave with the OAM mode number ofα,the emission signal of thenthelement can be expressed as whereβnis the phase error of thenthtransmitting-receiving channel,d=0,1,...,D-1 denotes thedthsub-pulse,Dis the total number of subpulses,f0stands for the carrier frequency of the first sub-pulse and Δfis the stepping frequency.For simplicity,in the case that the bandwidth is narrow compared with the central frequency,we consider that the phase error are fixed in the imaging process[28].

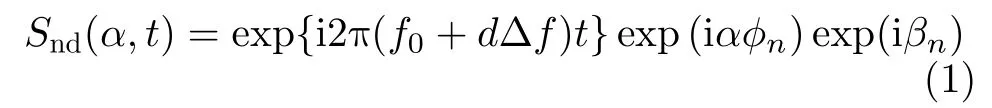
Fig.1 Vortex radar observation coordinate based on phased UCA

For a pointP(r,θ,φ) in far field,the coherent superposition of thedthsub-pulse emitted byNantenna elements is

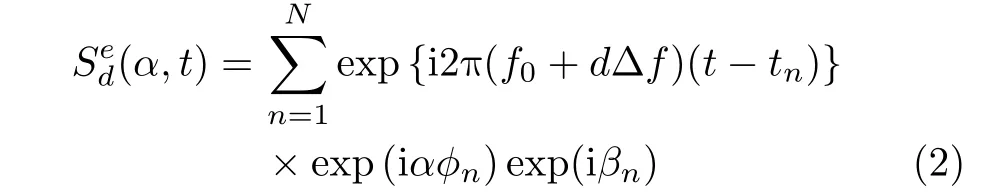
wheretn=|r-rn|/c≈()/c=t′-Δdn/c,ris the vector from origin to target centroid,rn=(acosϕn,asinϕn,0)represents the position vector of thenthelement,=(sinθcosφ,sinθsinφ,cosθ) is the unit vector ofr,t′=r/c,andΔdn==asinθcos(φ-ϕn).Meanwhile,adenotes the radius of the UCA,and c is the speed of light in vacuum.

Radar imaging usually satisfiest′≫Δdn/c,so

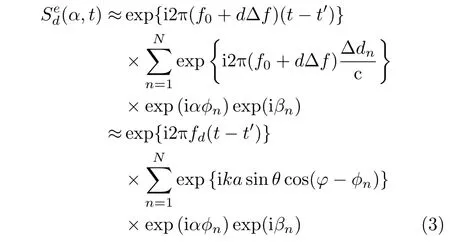
wherefd=f0+dΔf,andk=2πfd/c represents the wave number.

Assuming that the target to be detected is composed ofMideal scattering points,when the radar works in the multi-transmit and single-receive mode[9],that is,the single antenna located at the center of the circle is utilized to receive the target echo.Finally,the echo can be obtained as

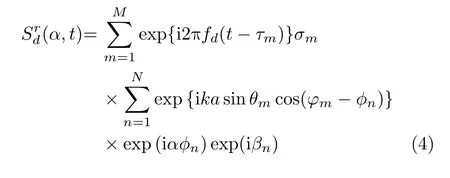
whereτm=2rm/c andσmrepresent the backscattering coefficient of themthscattering pointPm(rm,θm,φm).

After the down-converting procedure by the phase factor e xp{-i2πfdt},the echo signal in basis frequency can be expressed as

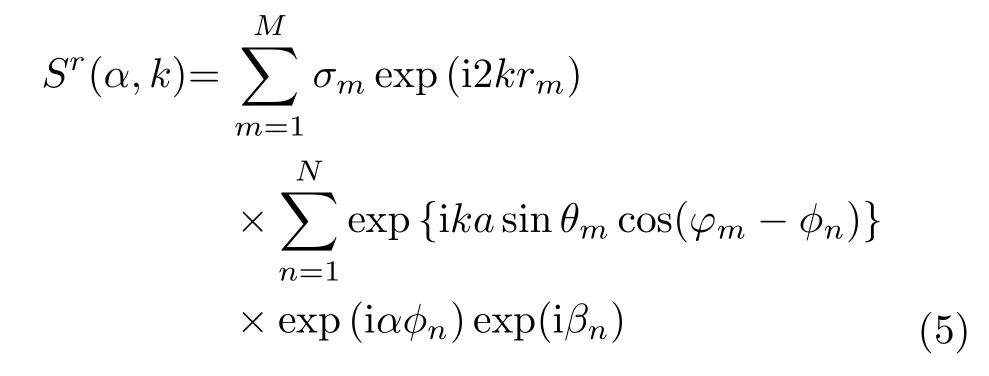
For simplicity of expression,the phase-independent window function term is omitted in Eq.(5).

The vortex wave imaging scene is divided intoMdiscrete grids.The number of observation values on the wave number domain and the OAM mode number domain arePandQ,respectively.Then,Eq.(5) can be written in the matrix form as

whereσ=[σ1,σ2,...,σM]T∈CMandnare the back scattering coefficient vector and the unknown noise vector,respectively.

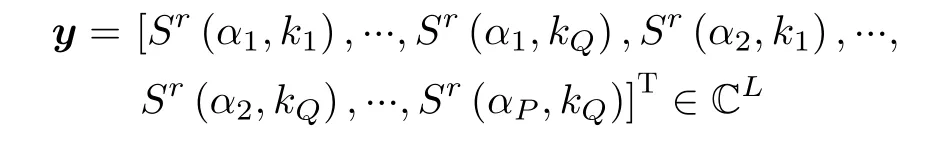
represents the received signal,whereL=P ×Q.In addition,S∈CL×Mindicates the measurement matrix,which is given by

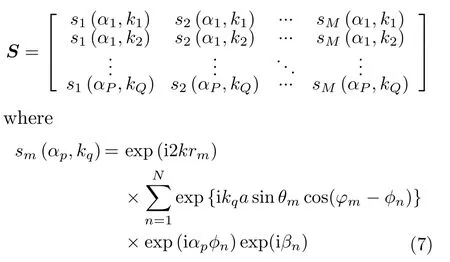
Obviously,Eq.(6) is a typical inverse problem.However,the observation matrix cannot be accurately calculated due to the existence of phase error,which may result in defocusing in traditional OAM imaging.For this reason,Eq.(6)is further rewritten into an inverse problem with unknown phase error parameterβ,

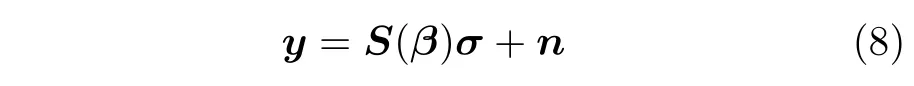
It is apparent thatσcould not be reconstructed directly by the conventional vortex radar imaging algorithms[16-18,29],especially under limited OAM modes,since the unknown parameterβexists.Therefore,a self-calibration imaging method is proposed to solve the problem in Section 3.

2.2 Analysis of imaging performance with phase error

In order to further explain the influence of phase error on the imaging performance of vortex radar,we will analyze it briefly from the perspective of PSF.

It can be seen from Eq.(5) that,the echo signal becomes an ideal echo model of multitransmit and single-receive mode[9]image mechanism when the phase error is zero.By approximation,it can be written in the form of weighted Bessel function[7]:

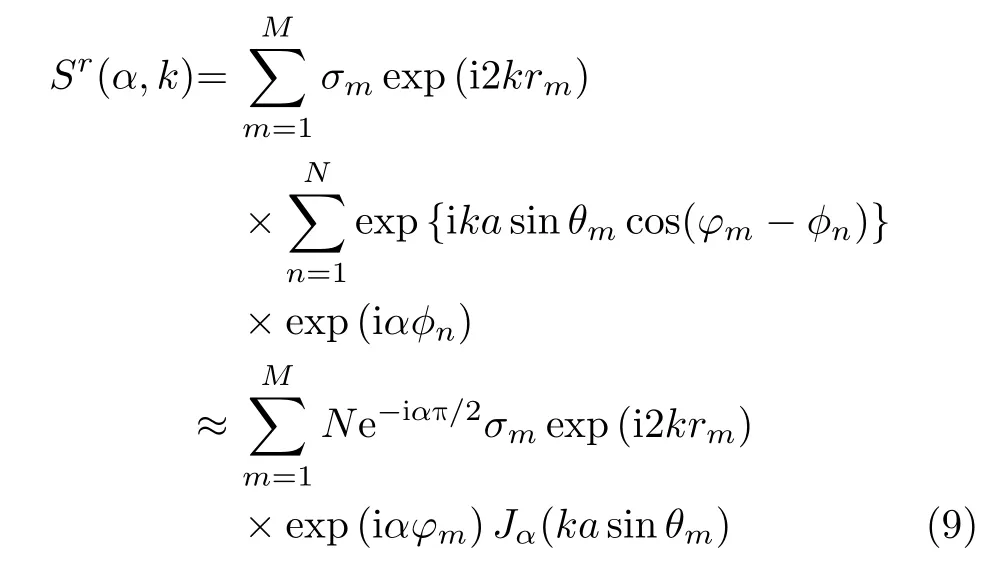
whereJα(·) indicates theαthorder Bessel function of first kind.Obviously,the target range and wavenumber form a Fourier duality,meanwhile,the azimuth and OAM mode is an approximate Fourier duality.After constant phase eiαπ/2and phase factorΨαcompensation[7,30],the Bessel function in the echo envelope is changed to its absolute value,where

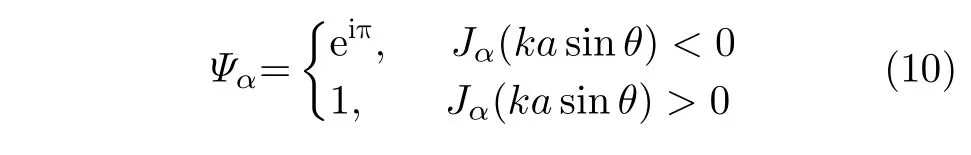
Hence,the PSF of the azimuth dimension under ideal condition is

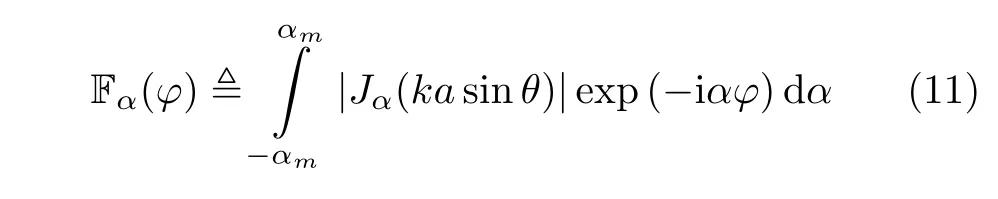
However,the sum of Eq.(5) can not be simplified into the weighted Bessel function form due to the existence of phase error factor.Moreover,it can be seen that each OAM mode is affected by the phase errors of all array element channels.This is caused by the particularity of vortex radar imaging mechanism.For vortex radar,the signals of multiple channels need to be combined into an OAM mode signal,and the echoes of different channels are correlative in the imaging process,which makes the analysis and processing of phase error for vortex radar imaging complex.Next we will give some brief analysis from the PSF perspective.

Under certain conditions,the phase error term in Eq.(5) can be a first-order Taylor expansion

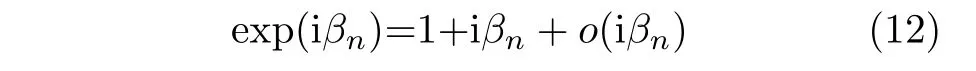
Furthermore,Eq.(5) can be rewritten as

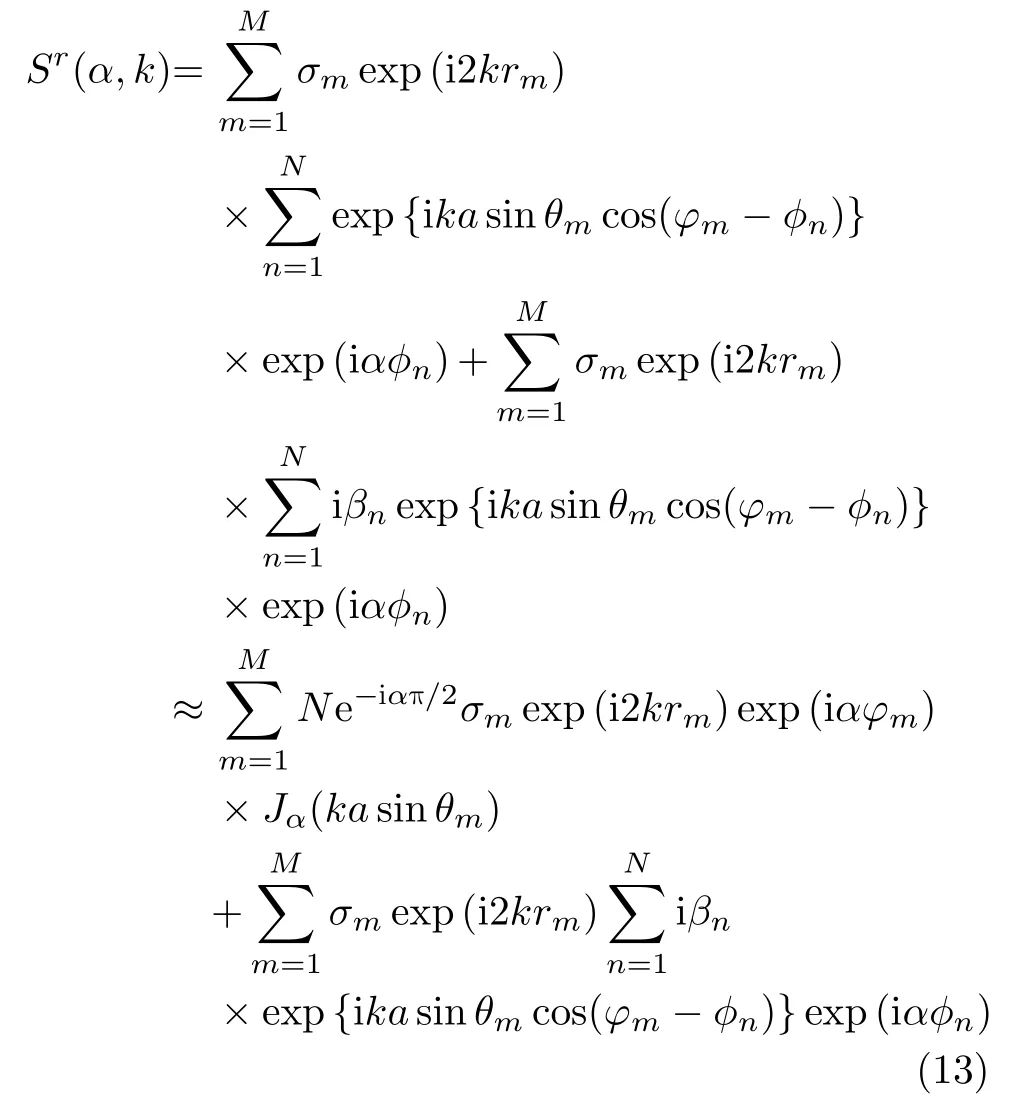
After the above constant phase eiαπ/2and phase factorΨαcompensation,the azimuth dimension PSF of vortex radar with phase error is

whereαmrepresents the maximum OAM modes.Apparently,the former term of Eq.(14) corresponds to the PSF of azimuth dimension when there is no phase error;and the latter term represents the influence of the phase error on PSF,which causes the defocus of imaging target,and affects the imaging performance.

In order to further illustrate the influence of the phase error on PSF,the point spread function is shown in Fig.2.And the blue solid line is the PSF without phase error,while the orange dotted line is the PSF with phase error.It illustrates that the PSF appears unimodal at zero when there is no phase error,which can focus well.However,the corresponding PSF becomes blurred and defocused when the phase error exists.

Fig.2 The azimuth dimension point spread function

3 Sparse Self-calibration Vortex Radar Imaging Method with Phase Error

In this section,a sparsity-driven high-resolution self-calibration method is proposed for vortex radar imaging with phase error.

From Bayesian perspective,the reconstruction of the target imageσand the estimation of the phase errorβin Eq.(8) can be written as follows:

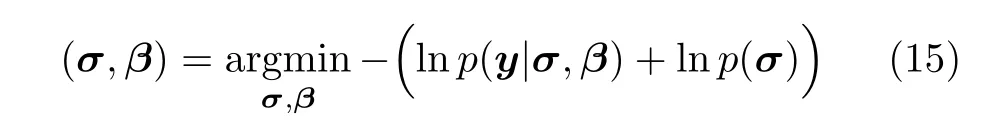
wherep(σ) andp(y|σ,β) are prior and likelihood respectively.

In order to solve the Eq.(15),an alternate iterative minimization method is proposed to achieve self-calibration imaging with phase error.The algorithm includes two steps in each iteration which are the target image reconstruction and phase error estimation.On the one hand,the proposed new structural sparse prior is utilized to promote sparse reconstruction of the imaging target by Bayesian inference.On the other hand,the phase error is estimated by the target image reconstruction results.Subsequently,the error is directly compensated to update the observation matrix.By alternating iterations of the two steps,the phase error can be compensated accurately and the image can be reconstructed with highresolution and high quality.Before the target reconstruction and phase error estimation,we first give the proposed structure sparse priori.

3.1 The proposed structure sparsity prior

The imaging targets usually have sparse characteristics in high frequency radar.Spike-andslab prior is widely utilized in the field of sparse signal recovery[31]and radar imaging[26].In the traditional spike-and-slab Sparse Bayesian Learning(SBL) framework,the target scattering coefficient vector is commonly assumed to be a point probability distribution (spike) and a Gaussian distribution (slab):

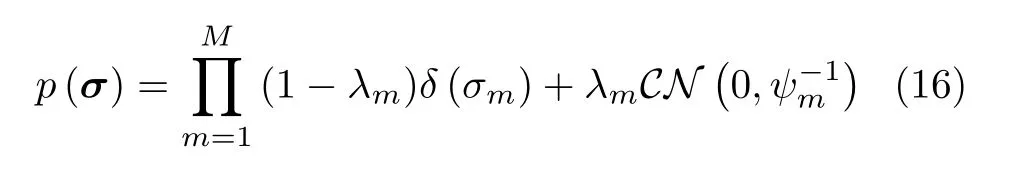
whereδ(·) is the Dirac delta function,is the complex Gaussian distribution.λandσdenote the support vector and the target scattering coefficient vector respectively.The varianceis decided by themthresolution cell scattering point.The support vectorλindicates the presence of scatterers in each resolution cell.

However,the presence of the delta function in Eq.(9) makes inference of posteriori troublesome by means of Bayesian learning theory.Therefore,we adopt a generalized spike and slab model[32],namely

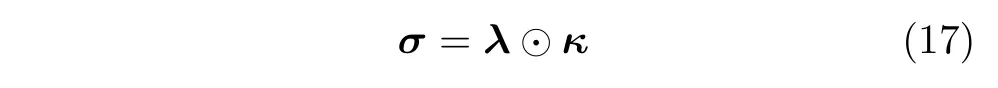
where,⊙is the Hadamard product,λis the support vector,andλm∈{0,1}.λm=1 indicates thatσmis non-zero andκis the backscattering coefficient vector.

In practical application scenarios,scatterers in radar images commonly present continuously since the real target is physically continuous[26,33,34],which may help to reconstruct radar images with limited measurements.Therefore,in order to model the structural correlation among adjacent scatterers,a novel structure sparse prior is proposed,in which the support vector of scattering coefficient and the target scattering coefficient vector are both correlated with their adjacent elements,i.e.

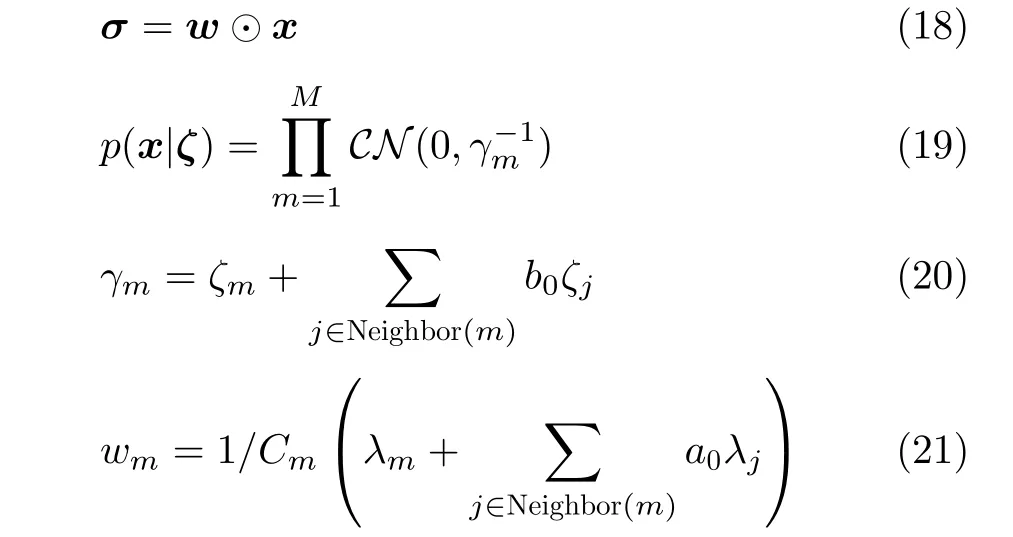
where Neighbor(m) represents the neighbor set of themthgrid cell,Cm=1+a0·Num is the normalized parameter,and Num denotes the element number of Neighbor(m).Moreover,a0,b0is the correlation parameters indicating the correlation between the scatterers and its neighbors.

The above prior represents that the sparsity among the scatterers are coupled through the correlation parameters,so as to promote better sparse structure characterization and achieve higher quality sparse imaging results.Furthermore,the proposed Bayesian prior model degenerates into the traditional spike-and-slab prior model whena0andb0are both zeros,which indicates that the more generality and extensibility of the proposed prior.

By the additive Gaussian noise assumption,the probability distribution of echo signalyis

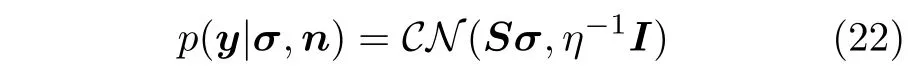
whereη-1is the variance of the additive noise.

In addition,for the convenience of conjugateexponential analysis,each component of the vectorλandζis assumed to be a Bernoulli-Beta prior and a Gamma prior,respectively.Meanwhile,ηis assumed to be a Gamma prior:

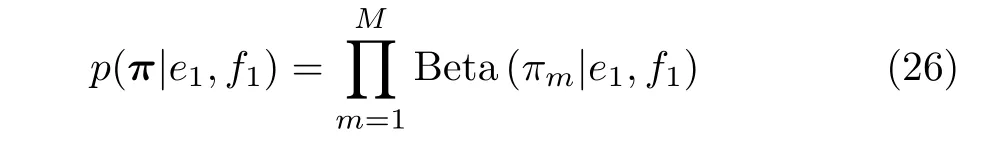
wherea1,b1,c1,d1,e1andf1are hyper-parameters.

3.2 Target image reconstruction

Firstly,the proposed structure sparse prior is applied to reconstruct target image.The reconstruction of the target imageσand the estimation of the phase errorβcan be written in Eq.(27)[35,36]based on the target sparse priors proposed in the subsection 3.1.

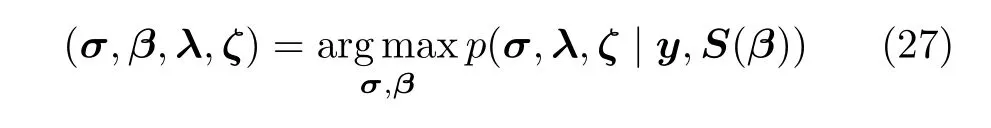
Namely,the posterior distributions ofσand the latent variablesλ,ζneed to be computed,while the likelihood distributions of phase errorβis estimated.

Generally speaking,Bayesian based signal reconstruction methods can be divided into several categories according to different variable inference approaches.Common Bayesian inference approaches are Variable Bayesian theory (VB)[35],Markov Chain Monte Carlo method (MCMC)[26],Approximate Message Passing(AMP)[37],etc.In the paper,we use VB to perform parameter inference since the VB technique has been shown to provide accurate and effective inference for spikeand-slab models[25].

The main idea of VB is to optimize the lower bound of the log marginal likelihood function,and simultaneously give a maximum for the posterior distribution.Next,the specific process of algorithm update is deduced by VB theory under the assumption that the phase errorβis known.

(1) Update forx

The posterior distribution ofxcan be written as

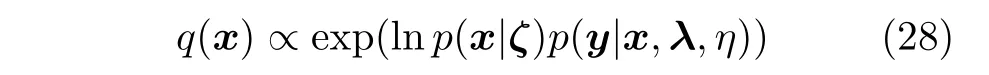
Apparently,q(x) is a multivariate Gaussian distribution,with meanµand variationΣ,i.e.,x～CN(x;µ,Σ),with

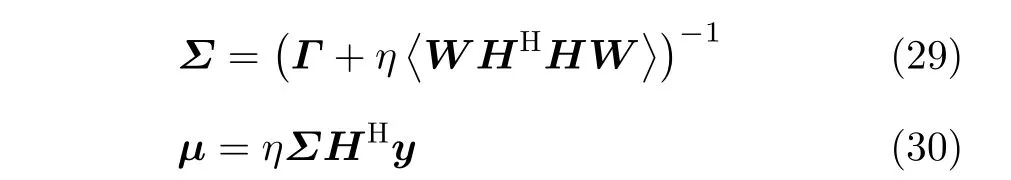
whereΓ=diag(γ),W=diag(w).Given the updated valuew,we can derive

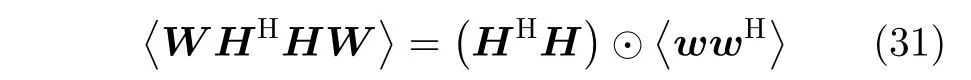
(2) Update forλ

For each element ofλ,the posterior could be given as

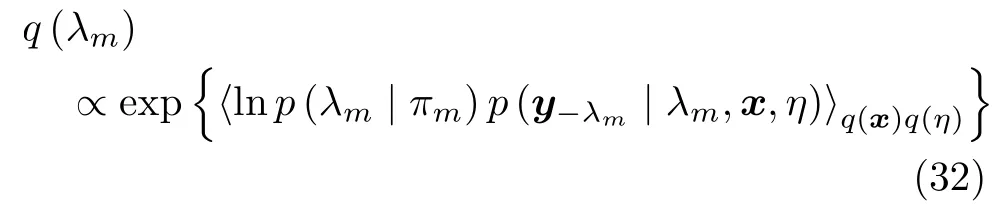
λmobeys the Bernoulli distribution,and its distribution parameters can be calculated as

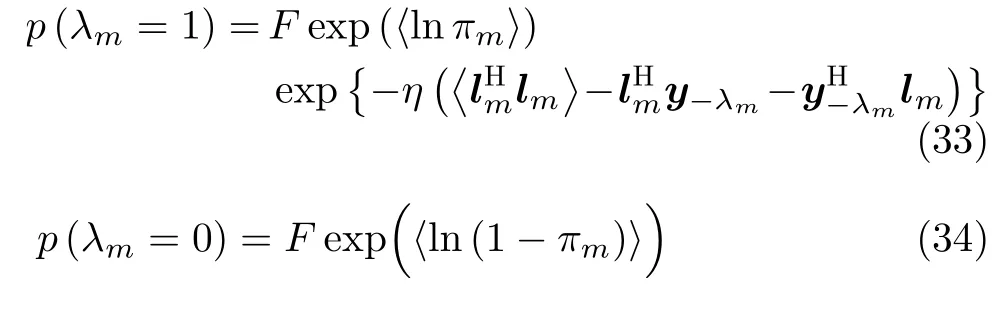
whereFis a normalized parameter such thatp(λm=1)+p(λm=0)=1,and

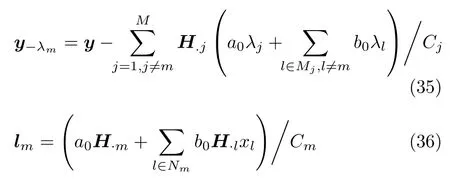
In addition,the update forπmcould be referred by Eq.(41) in following subsections.And whenµ,Σis obtained,we can calculateby

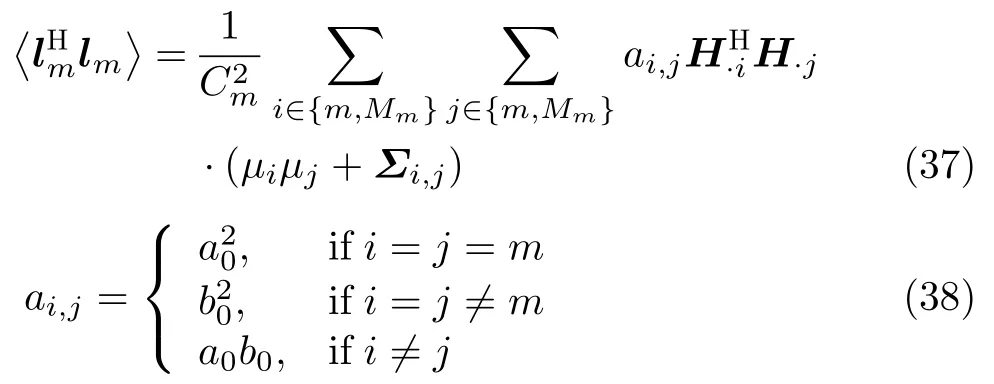
Therefore,λcan be updated by

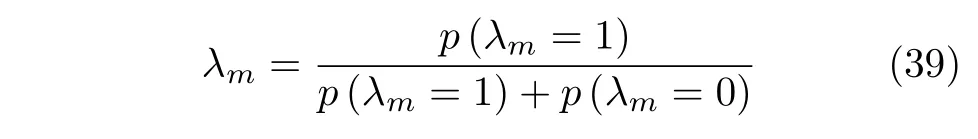
After obtaining the update ofxandλ,we will derive the update of the latent variablesπ,η,andαin this subsection.

(3) Update forπ

The approximate posterior distribution ofπis

It’s easy to verify thatπis a Beta distribution,i.e.

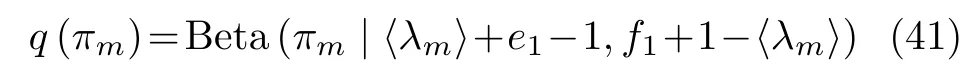
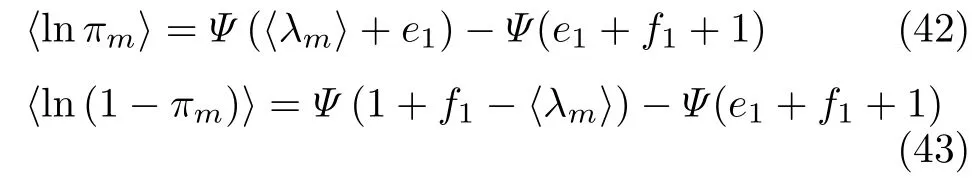
whereΨ(·) is a digamma function.

(4) Update forη

The approximate posterior distribution ofηis a Gamma distribution

Thereforeηcan be updated by

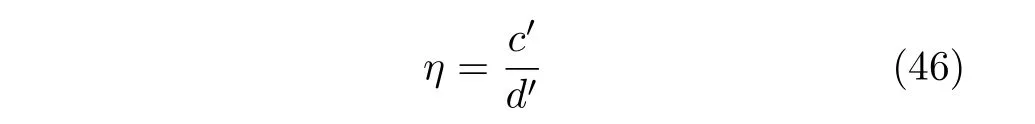
(5) Update forζ

For the parameterζ,the posterior distribution is

Plug Eqs.(19) and (20) to Eq.(47),we can get

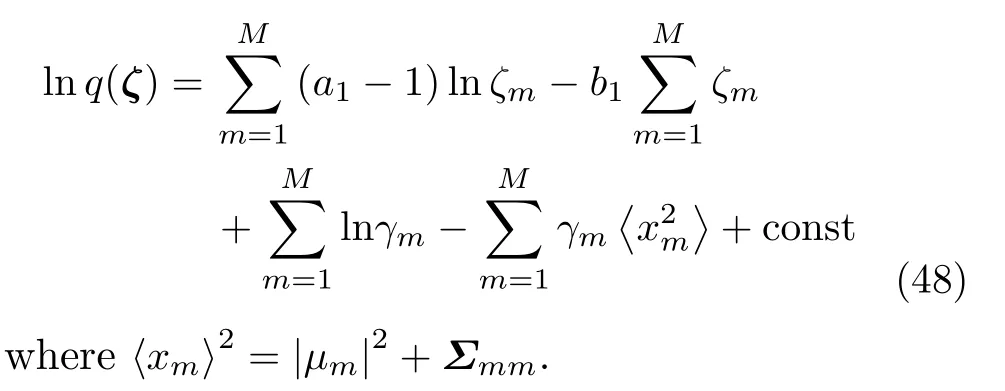
The strict posterior distribution ofζis intractable to derive an analytic solution,However,an appropriate approximate can be obtained by using the similar processing method in Ref.[33],

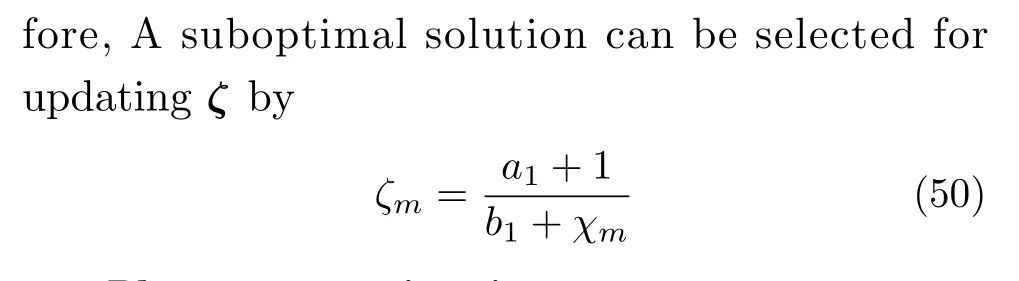
3.3 Phase error estimation

Phase error estimation can be regarded as an unknown deterministic parameter estimation problem[38].In this subsection,phase error is estimated by the maximum likelihood estimation method,and it can be estimated as

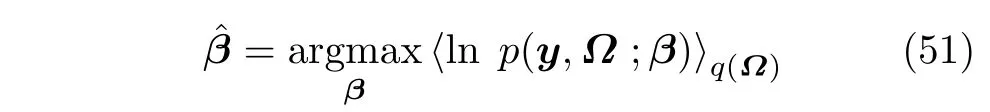
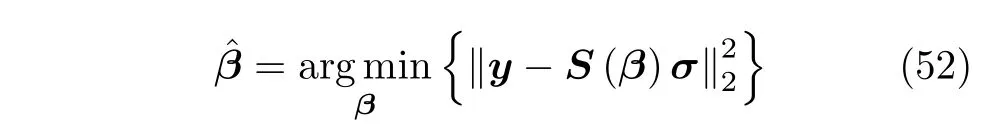
Hence,the estimation ofβis a nonlinear optimization problem which is not tractable to obtain a closed-form solution.Therefore,gradient descent method is utilized.This paper employs the Newton method to updateβ:

where Re(·) and I m(·) denote the real and imaginary part respectively,and

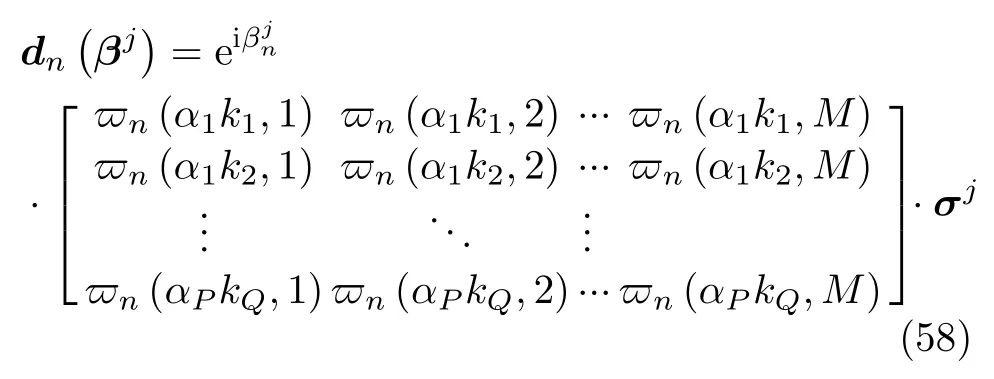
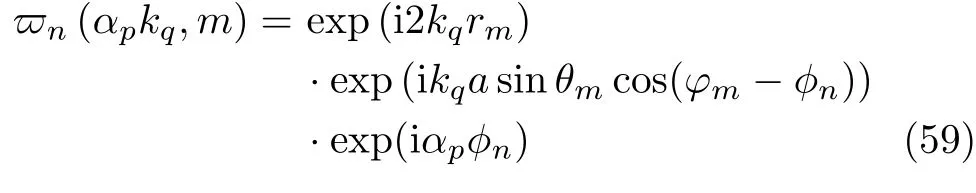
Finally,the procedure of proposed algorithm for vortex radar self-calibration imaging with phase error,called VSCIP,is summarized in Algorithm 1.The algorithm is an iterative algorithm,which alternately iterates through steps of target image reconstruction,and phase error estimation until meeting the termination condition.

3.4 Algorithm performance analysis

After investigating the proposed algorithm in depth,we offer some discussions to gain insight into the algorithm.

(1) The optimal solution:Although the proposed two-step iteration method is utilized to solve the problem,the above optimization problem is still a non-convex problem.Therefore,the proposed method still has a probability of falling into the local optimal solution.In general,increasing the number of equations is an effective means to decrease the probability of falling into the local optimal solution,but it increases the computational complexity.During the procedure,the higher order statistical information (such as the estimation covariance matrix) is utilized to enhance the estimation performance and avoid converging to a shallow local minimum in the full Bayesian framework[38,39].Moreover,the proposed algorithm can properly employ uncertainty information during iterations to ameliorate the error propagation problem,which means the estimation error of the sparse signal would degrade the estimation accuracy of phase error during iterations.In addition,it is another option to avoid deviating too far from the true minimum by limiting the step size of gradient descent[28].

(2) Convergence:Since the proposed VSCIP algorithm can be interpreted as a variational EM algorithm,the update ofσandβwill monotonically decrease the KL divergence and the negative expected log-likelihood function,respectively,until convergence[39].Thus,the (marginal) likelihood monotonically increases during the iterations and the convergence is guaranteed.

(3) Computational complexity:The main computational burden at each iteration of proposed algorithm comes from the update ofµ,Σin Eqs.(29) and (30),and the update ofβin Newton’s method.The main time-consuming operations are the matrix inversion and matrixvector multiplication whose computational complexity areo(K3) ando(K2),respectively.This can incur a high computational cost whenKis large.Fortunately,the grid pruning[38]could reduce the computational burden and improve the convergence speed,as the remaining grid number after pruning decreases fast.Moreover,the computational burden can also be controlled by limiting the maximum number of iterations.

4 Simulation Results

In this section,simulations are performed to evaluate the performance of the proposed algorithm.All computations are run using MATLAB in Windows 10 on an Intel Core i5-8500 CPU at 3.00 GHz.

This paper divides an imaging scene with size of 30 m ×0.4π into 41 × 41 grids,the imaging distance is set to 1000 m in all the simulations.An X-band UCA system with carrier frequency of 10 GHz is considered.Besides,the radar system consists of 22 transmitters and one receiver,and the phase errors are uniformly varying at [-20°,20°][40].The key radar parameters are given in Tab.1,complex white Gaussian noise is added in the imaging process.

Tab.1 Key radar parameters for simulations

For comparison,the traditional imaging method OMP[18,41],TwIST[42],and SBL[16,36]are utilized to vortex EM imaging without phase error calculation.In addition,TV-TLS[43],a commonly method with strong fault tolerance in radar imaging,is also utilized as a contrast.It prefers to compensate the perturbation matrixErather than directly compensate phase error and it aims to find the solution of the following optimization problem:

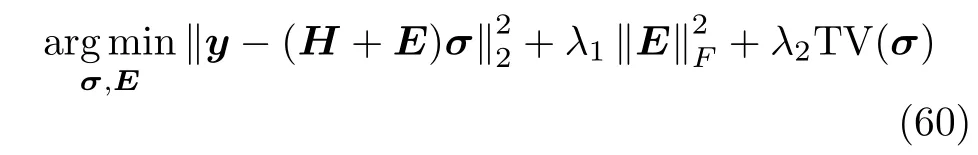
where T V(σ) represents the total variation regularizer,besides,λ1andλ2are regularization parameters.

To quantitatively describe the image reconstruction results,two metrics are defined,e.g.the Normalized Mean-Square Error (NMSE) and the image correlation value:

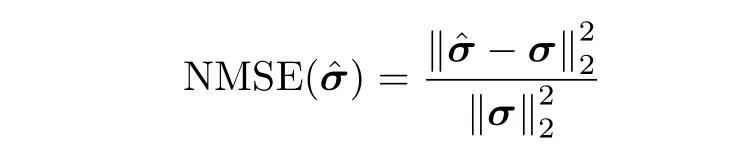
whereas image correlation value is defined as

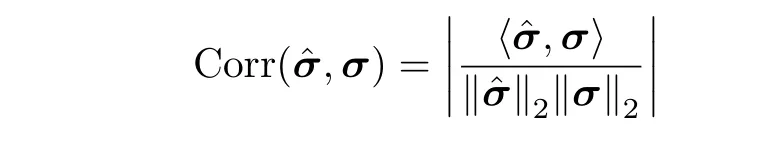
whereandσare reconstructed images and true images respectively.Moreover,the higher thevalue of NMSE() and the smaller the value of Corr()represent the better result of imaging.

4.1 Imaging simulations with phase error

To verify the effectiveness of the proposed method,the following simulations are carried out.

Firstly,we illustrate the effect of phase error on imaging.The key radar parameters are given in Tab.1,and the Original target 1 scene is shown in Fig.3(a).Moreover,the SNR is set to be 20 dB.

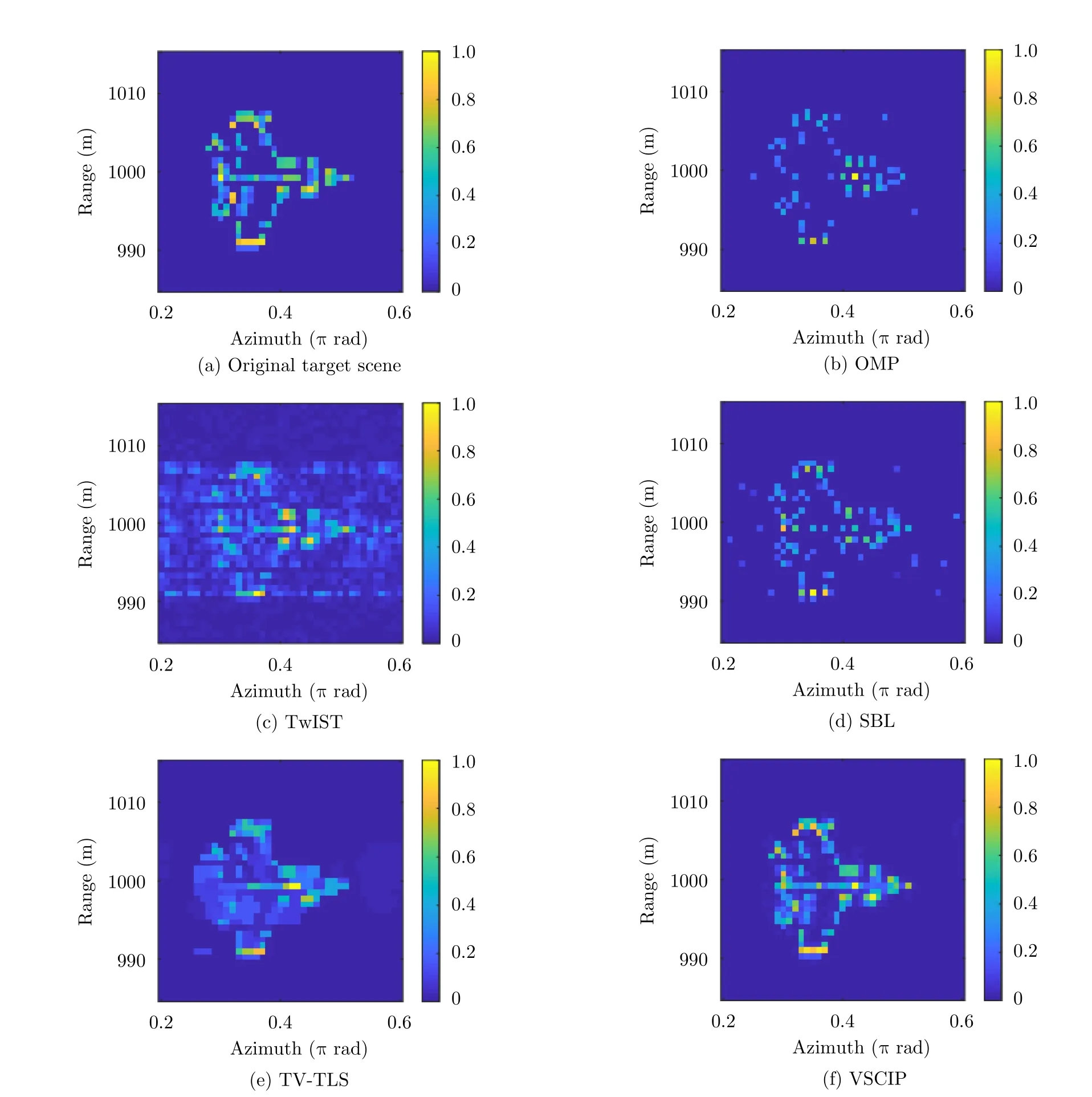
Fig.3 In mode number [-10,10],the obtained vortex EM images with phase error using different algorithms for SNR=20 dB

The reconstructed images by traditional methods OMP,TwIST and SBL are given in Fig.3(b)-Fig.3(d).It can be seen that,both of OMP and TwIST methods fail to reconstruct the target images.Especially,the reconstruction result of OMP is almost completely missing the target contour,and the imaging result of TwIST is seriously blurred.Meanwhile,there were many false target points in the reconstructed images by SBL,and the imaging results cannot be identified by the outlines of the reconstructed images due to the non-consideration for phase errors.Relatively speaking,the result of TV-TLS is little better than those of the OMP and TwIST since the observation matrix has an additive error perturbation,and the contour is slightly clearer,due to the effect of TV regularization.However,TVTLS imaging results are partially missing and blurred.Compared with the above methods,the reconstructed image obtained by the algorithm proposed in this paper,VSCIP,has better imaging performance.The image result is illustrated in Fig.3(f),where the main scatterers of the target are all preserved,and the contour edge is clearer.Investigate its reason,the support vectorλlearns the spatial distribution of target scatterers with the iteration of the proposed methods.More concretely,for the gird cell without scatterers,λmgradually become zeros,while for the gird cell with scatterers,λmkeeps non-zero value.At the same time,ζmgradually becomes a big number for the gird cell without scatterers.In addition,the parameters affect the estimation of the parameters in surrounding gird cells.Hence,when the final convergence is achieved,the proposed prior appreciably models the cluster sparse structure of the target.Moreover,since a calibration step for phase errors is performed in the proposed methods,the reconstructed images obtain better imaging results and the main scatterers of target are all preserved.

Then,in order to further illustrate the effectiveness of the proposed self-correction algorithm,the estimated and real phase error are shown in Fig.4(a).It clearly shows that the unknown phase error can be accurately estimated,which provides further support for the algorithm to better reconstruct the target image.

Finally,the curve of NMSE(σˆ) versus the number of iterations is shown in Fig.4(b).It can be seen that NMSE(σˆ) gradually decreases with the number of iterations and converges quickly,which further illustrates the convergence of the algorithm.

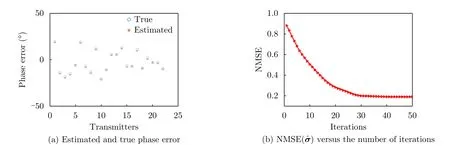
Fig.4 The proposed self-calibration algorithm performance

4.2 Phase error estimation performance evaluation

To quantitatively evaluate the accuracy of phase error estimation,the Normalized Mean-Square Error (NMSE) of phase error is defined as

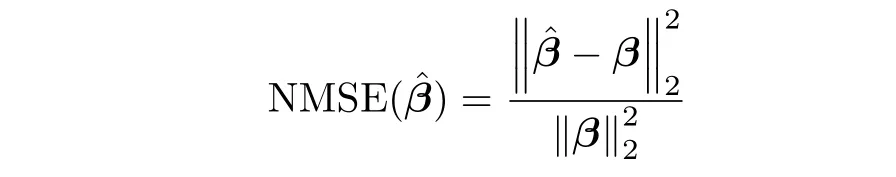
whereandβare evaluated and true phase error respectively.

Firstly,the NMSE() of phase error under SNRs from-10 to 40 dB is illustrated in Fig.5(a),It can be seen that the accuracy of phase error estimation improves with the increase of SNR.When the SNR is low,the estimation performance of phase error is unsatisfactory.

In addition,the performance evaluation of phase error estimation under different phase error range is executed.In the simulation,the phase errorβis uniformly selected in[-Δd,Δd]degree.And Δdare set from 5 to 30 respectively.Moreover,the SNR is set to be 20 dB.The other parameters are the same with those in Tab.1.The N MSE() of phase error under different phase error range is shown in Fig.5(b).Obviously,the NMSE()increases with phase error range widening.And the estimation performance of phase error is poor when Δdis above 20.

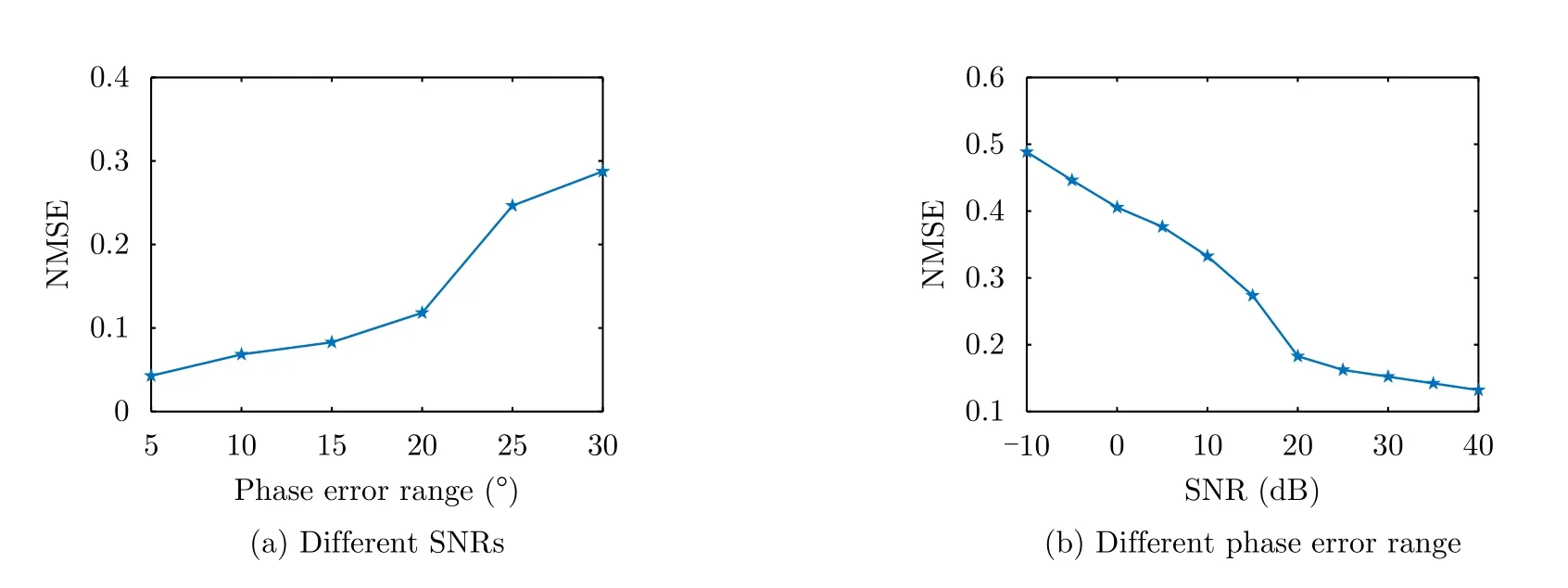
Fig.5 NMSE() of phase error under different SNRs and different phase error range

4.3 Imaging performance evaluation under different SNRs

In order to verify the robustness to the noise of the proposed method,the following simulations are carried out in different echo SNRs.

The imaging results of different methods at SNR=5 dB are shown in Fig.6.Compared with the results of SNR=20 dB with a high SNR,the imaging performance of all the algorithms is slightly decreased.However,it can be seen that the imaging effect of the proposed algorithm is still significantly better than the imaging results of other methods,both in terms of imaging clarity and target contour.

Fig.6 In mode number [-10,10],the obtained vortex EM images of target 1 scene with phase error using different algorithms for SNR=5 dB

Then,in order to quantitatively describe the imaging performance of the proposed algorithm at different SNR levels,The NMSEs ofand image correlation values diagram of aforementioned algorithms for SNRs from -10 to 40 dB are given in Fig.7,with 50 independent Monte Carlo trials for each method.And it can be seen that the NMSE()decreases while the C orr() increases with the increasing of the SNR level.

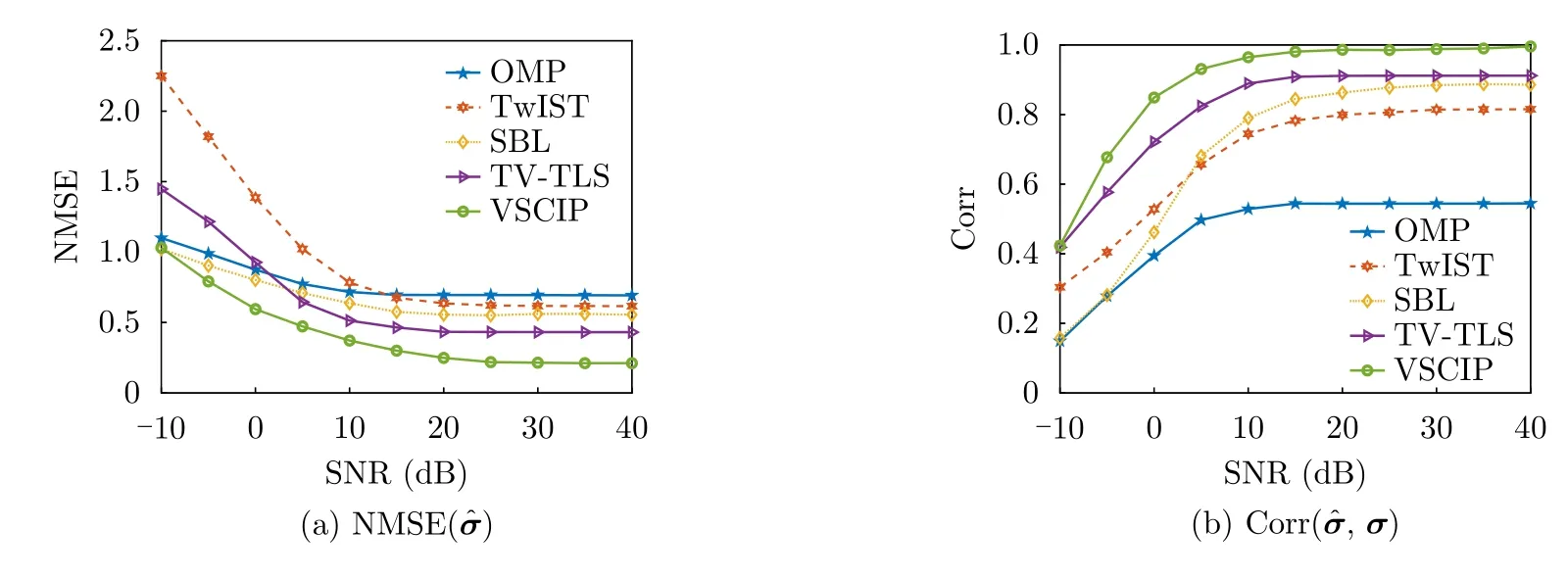
Fig.7 Under different SNRs,and obtained of original target 1 scene in mode number [-10,10]

In addition,it can see that the NMSE() of the proposed algorithm under all SNRs is lower than or equal to that of other algorithms.Meanwhile,the Corr() of the proposed algorithm under all SNRs is higher than that of other algorithms.And when SNR is higher than 15 dB,the Corr() value is almost close to 1.Therefore,we can prove the superiority of the proposed algorithm and its robustness to noise.

4.4 Imaging performance evaluation under different target scenes

Since the proposed self-calibration vortex radar imaging algorithm is based on the prior assumption of sparse targets,the imaging reconstruction performance may be affected by the target,or more accurately,the sparsity of the target.In this subsection,we will design simulations to compare the imaging performance under different target scenarios.

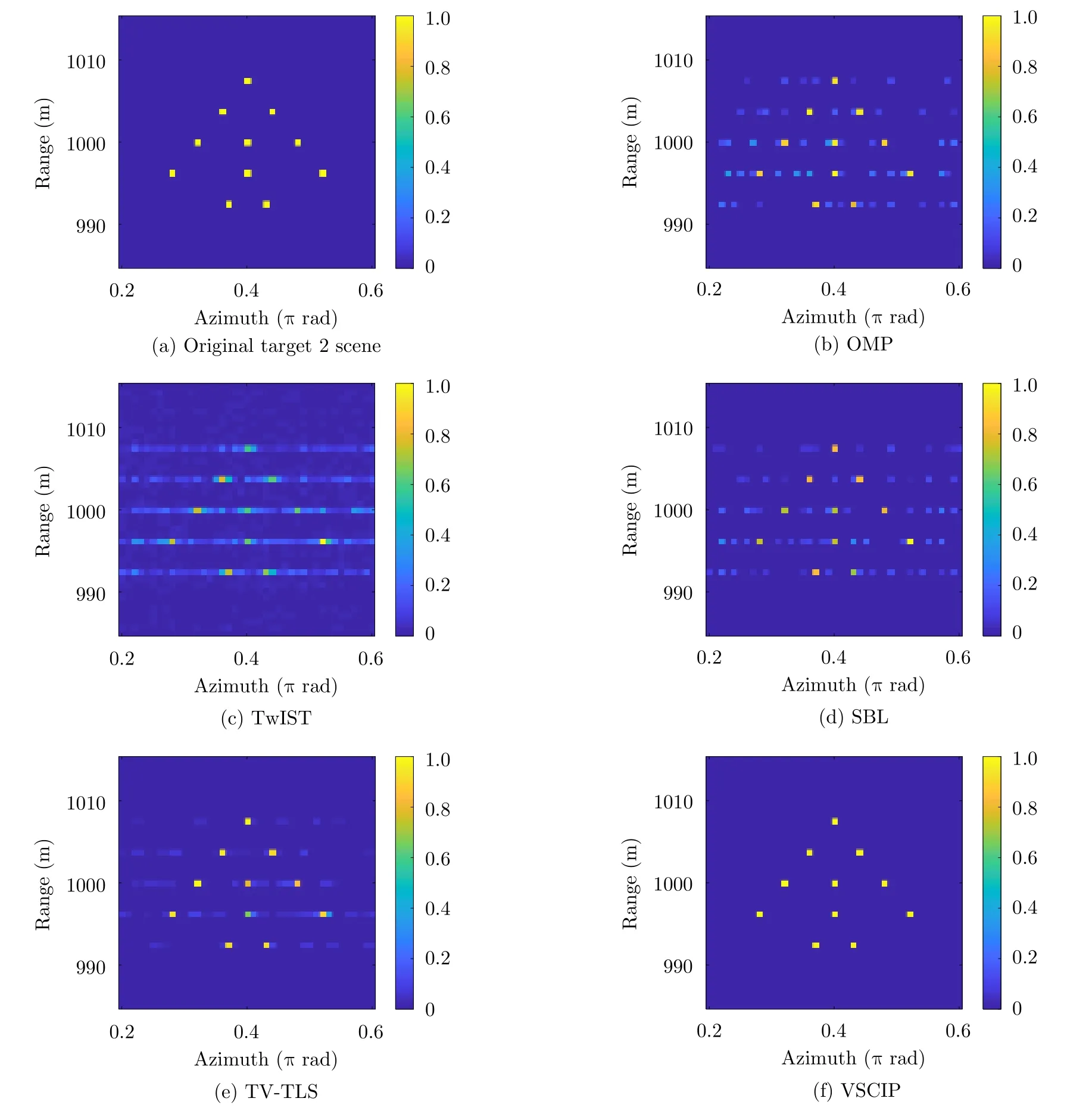
Fig.8 In mode number [-10,10],the obtained vortex EM images of target 2 scene with phase error using different algorithms for SNR=20 dB

When SNR is 20 dB,the imaging results of target 2 and target 3 scenes under the above algorithms are shown in Fig.8 and Fig.9 respectively.

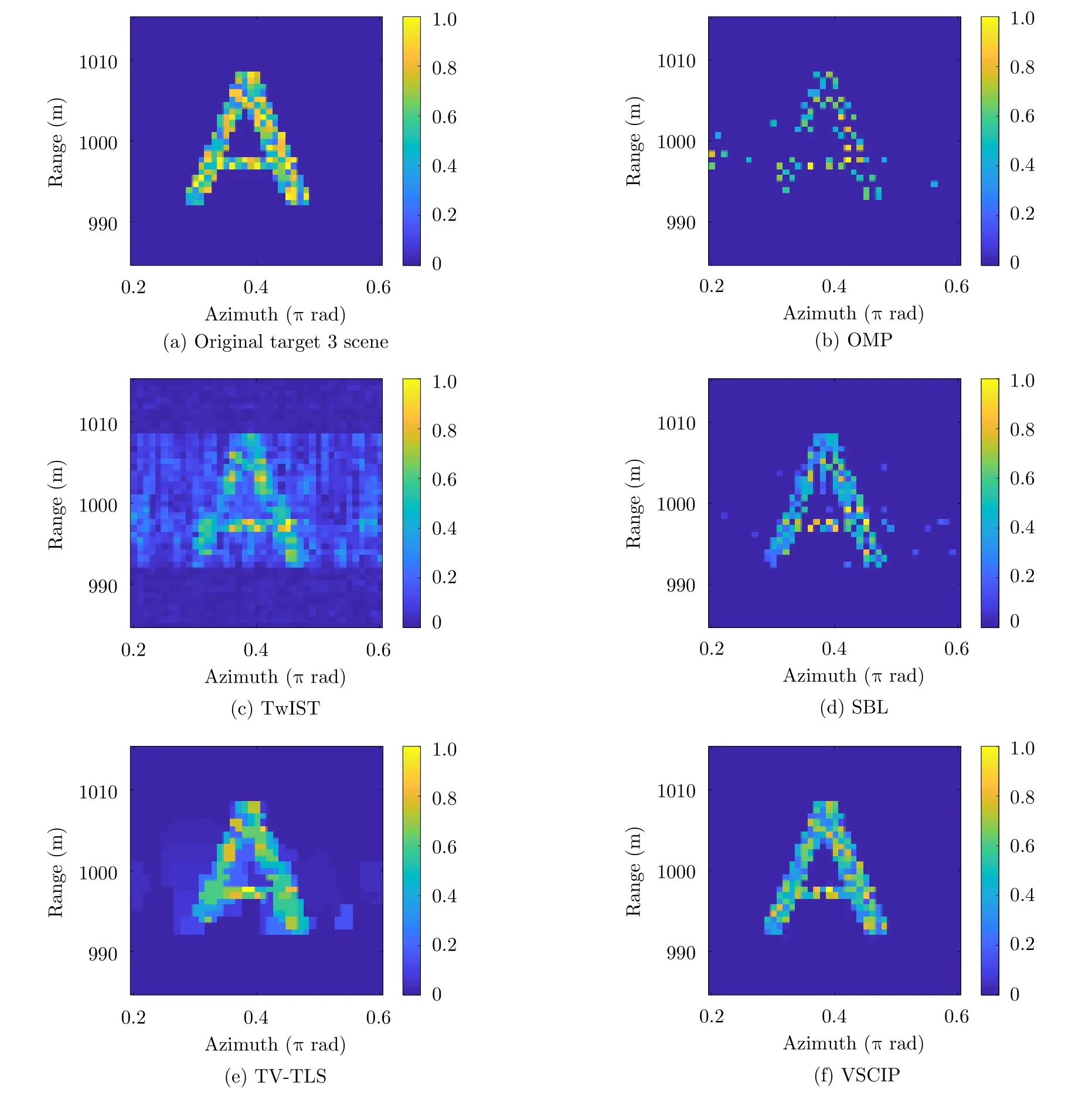
Fig.9 In mode number [-10,10],the obtained vortex EM images of target 3 scene with phase error using different algorithms for SNR=20 dB

On the one hand,for point target 2 with strong sparsity,it can be intuitively seen from the imaging results in Fig.8 that the imaging results of the proposed algorithm are relatively clear and have excellent performance.However,the imaging results of other methods more or less have some false points,and the recovery intensity of scattered points of some targets is low.On the other hand,for target 3 with a certain continuity structure and weak sparsity,the reconstructed result of OMP algorithm has serious contour loss and some false points,and the image background of Twist algorithm is rough,meanwhile the target contour is fuzzy.Compared with the above two methods,the imaging result of SBL is improved to a certain extent,but there are also many false points,and the local region is fuzzy.In addition,TV-TLS imaging is slightly blurry,and the local position is slightly missing.However,the imaging results of the proposed algorithm are clear,and there is no false point target,and the imaging effect is superior.

In order to further quantitatively demonstrate the imaging performance under different targets Scenes,the NMSE() andCorr()curves of target 2 and target 3 under different SNRs are illustrated in Fig.10 and Fig.11 respectively.It can be apparently seen that the proposed algorithm has the smallest NMSE() and the largest Corr() value under all SNRs compared with other algorithms regardless of target 2 or target 3.This is similar to the previous result of target 1.In summary,it can be concluded that the method proposed in this paper has favorable effectiveness and strong adaptability,which further verifies the superiority and scalability of the proposed target prior.

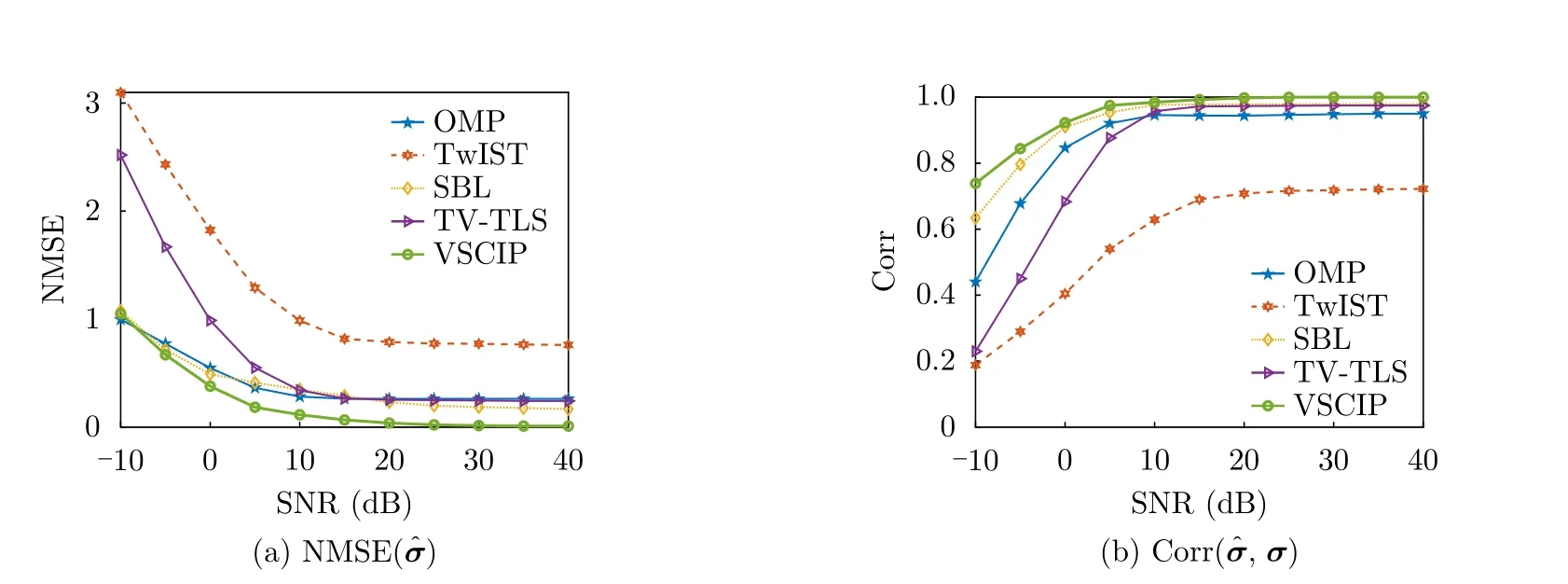
Fig.10 Under different SNRs,N MSE() and C orr(,σ) obtained of original target 2 scene in mode number [-10,10]

Fig.11 Under different SNRs,N MSE() and C orr(,σ) obtained of original target 3 scene in mode number [-10,10]

5 Conclusion

To summarize,the vortex radar imaging with phase error is theoretically analyzed and modeled,meanwhile,a novel self-calibration algorithm for alleviating the issue is proposed in this paper.As an alternating iterative algorithm,the proposed method cycles through steps of target reconstruction and phase error estimation to reconstruct the target accurately and compensate the phase error effectively.Wherein the variable Bayesian theory is introduced to update the posterior of the target image,and maximum likelihood estimation is adopted to estimate the phase error.The proposed method can reconstruct the target with high imaging quality and accurately compensate the phase error.Furthermore,simulation results illustrate the effectiveness of the proposed method in the presence of phase errors and the robustness to noise,meanwhile the proposed method has excellent adaptability to image targets with different sparsity and structure distribution characteristics.Further research will include illustrating the effectiveness of proposed method by measured experiments,and exploring the imaging approaches of moving targets in practical scenarios.