涡旋雷达成像技术研究进展

郭忠义 王运来 汪彦哲 郭 凯

(合肥工业大学计算机与信息学院 合肥 230009)

1 引言

随着现代科学技术不断发展，人们对雷达成像的分辨率要求也越来越高。而传统雷达成像技术实现高分辨率成像往往依赖于距离多普勒原理[1-3]，即通过发送宽带的信号实现目标在距离向的高分辨率，并通过雷达与目标之间的相对运动形成较大的虚拟孔径，从而获得目标在横向的高分辨率。然而，当雷达与目标无法进行较大的相对运动，甚至不能发生相对运动时，就无法形成较大的虚拟孔径，从而降低了雷达的横向分辨率。对于实孔径雷达而言，其横向的分辨率与它的实孔径大小有关，而在实际应用中无法获得巨大的真实孔径，导致实孔径雷达的横向分辨率较低。以上难题限制了雷达成像技术的发展，因此需要寻找新的雷达体制去解决这些难题。

携带有轨道角动量(Orbital Angular Momentum,OAM)的电磁波的波前呈现螺旋状结构[4]，因此携带有轨道角动量的电磁波被称为涡旋电磁波，而且由于涡旋电磁波的模式具有无穷性和相互正交性[5]，所以涡旋电磁波的模式可以作为等价于极化、频率之外的一种新的维度。因此涡旋电磁波不仅得到了国内外学者的广泛研究，还为突破传统雷达成像技术的瓶颈提供了一条可行的途径。1992年，荷兰物理学家Allen等人[6]发现拉盖尔高斯(Laguerre-Gauss,LG)光束携带有轨道角动量，还确定了轨道角动量与OAM态之间的关系。之后在涡旋光的产生、传播、量子操控等方面的应用[7-12]都得到了国内外学者的广泛研究。轨道角动量不仅在光波段中进行了研究，在声波段[13-15]、射频波段[16-20]中也有大量的研究。轨道角动量在射频波段的研究相比于光波段要晚一些，2005年，Trinder[16]设计抛物面反射型天线首次在无线电频段产生了携带OAM的电磁波。2007年，Thidé等人[17]提出了采用均匀排布的圆形阵列产生无线电频段涡旋电磁波的方法，并对产生的涡旋电磁波的辐射场进行了分析。此后，涡旋电磁波的产生[18-27]、无线通信[28,29]、旋转物体的旋转速度检测[30,31]、雷达成像[32-38]等方面引起了众多学者的广泛研究。

已有研究表明，当涡旋电磁波的辐射场照射到目标上时，雷达接收到的回波信号中包含有目标方位向的信息[32]。因此使用涡旋电磁波进行雷达成像时，可以通过信号处理的手段从回波信号中获取目标方位向的信息。所以使用涡旋电磁波进行雷达成像时，雷达与目标之间不需要发生相对运动就可以获得对目标在方位向的分辨能力，且雷达在方位向的分辨率与使用的模式数的区间长度成正比。因此，从回波信号包含目标信息量的角度看，涡旋雷达相比于现有雷达体制有很大的潜在优势。但是涡旋电磁波本身存在的问题，如波束中空和产生的涡旋电磁波在远距离传输时纯度降低等，使其在实际应用时受到一定的限制。因此相比于其他雷达方法，涡旋雷达的缺点是随着传输距离的增大，其波束中空导致无法成像的空域亦增大，同时涡旋电磁波的纯度下降，从而导致成像误差也增大。

近些年来，国内已经有很多研究人员提出多种使用涡旋电磁波进行雷达成像的模型[32-36]，并针对这些雷达成像模型提出了相应的雷达成像算法[37-43]，实现了对目标的一维和二维成像。通常，对目标的一维和二维成像不能满足所有的需求，因此国内研究人员将涡旋电磁波与合成孔径雷达(Synthetic Aperture Radar,SAR)技术和逆合成孔径雷达(Inverse Synthetic Aperture Radar,ISAR)技术结合[44-46]，实现了对目标的三维成像。相比之下，国外课题组的研究人员更关注于涡旋电磁波技术中的涡旋态探测[47,48]，而对于涡旋雷达成像技术的研究进展较为缓慢，意大利的Loreto Di Donato课题组[49]利用波恩近似，实现了利用涡旋电磁波对目标的二维层析成像。

本文针对涡旋雷达成像技术更进一步地进行了较为全面的总结，主要从3个方面介绍，分别是涡旋雷达成像模型、涡旋雷达凝视成像算法和涡旋雷达运动成像。涡旋雷达成像模型以成像过程中涡旋电磁波收发方式的不同进行区分，不同收发方式的涡旋雷达成像的物理过程不尽相同，因此雷达在方位向的分辨率和雷达成像效率也不尽相同；因为涡旋电磁波具有多重特点，所以涡旋雷达凝视成像算法是在凝视成像的场景下根据利用的涡旋电磁波的特点不同进行区分的，大致可分类为谱估计和稀疏恢复两大类算法；涡旋雷达运动成像是雷达与目标之间存在相对运动的场景下的涡旋雷达成像，涡旋雷达运动成像主要的模型与算法是对SAR和ISAR的模型与算法针对涡旋电磁波的特点进行一些改动得出的。本文内容总共分为4个部分，第1部分为引言，概述了传统雷达成像存在的问题和涡旋雷达成像的起源；第2部分对涡旋电磁波的基本特性、产生方法和成像原理进行了介绍；第3部分重点介绍了涡旋雷达成像模型、涡旋雷达凝视成像算法和涡旋雷达运动成像的研究进展；第4部分简单概括了涡旋雷达成像技术未来的应用前景，以及该研究领域未来的重点和难点。

2 涡旋电磁波及其成像原理

2.1 涡旋电磁波

根据经典电动力学[50]，电磁波不仅有线动量，还有角动量。而电磁波的角动量又分为自旋角动量(Spin Angular Momentum,SAM)和轨道角动量(OAM)。携带有轨道角动量的电磁波在与其传播轴垂直的平面上，强度分布具有类似于“甜甜圈”的结构，其相位随着方位角发生线性变化。在空间中其相位波前呈现出螺旋状，因此携带有轨道角动量的电磁波也被称为涡旋电磁波。涡旋电磁波携带的轨道角动量的模式数等于其相位随着方位角的线性变化率l，涡旋电磁波携带的轨道角动量的模式数又被称为拓扑荷数，涡旋电磁波的电场矢量的表达式为

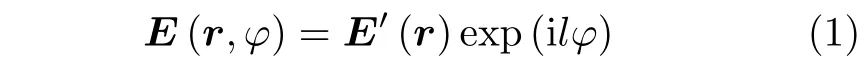
其中，E′(r)为传统平面波或者球面波的电场矢量，φ为投影到与传播轴垂直面上的方位角。图1为不同OAM态的涡旋电磁波的相位和强度分布[51]。从式(1)可以发现，涡旋电磁波的相位不仅与距离r有关，还与方位角φ相关，因此涡旋电磁波相对于平面波额外提供在波束内同距离不同方位角的分辨力。

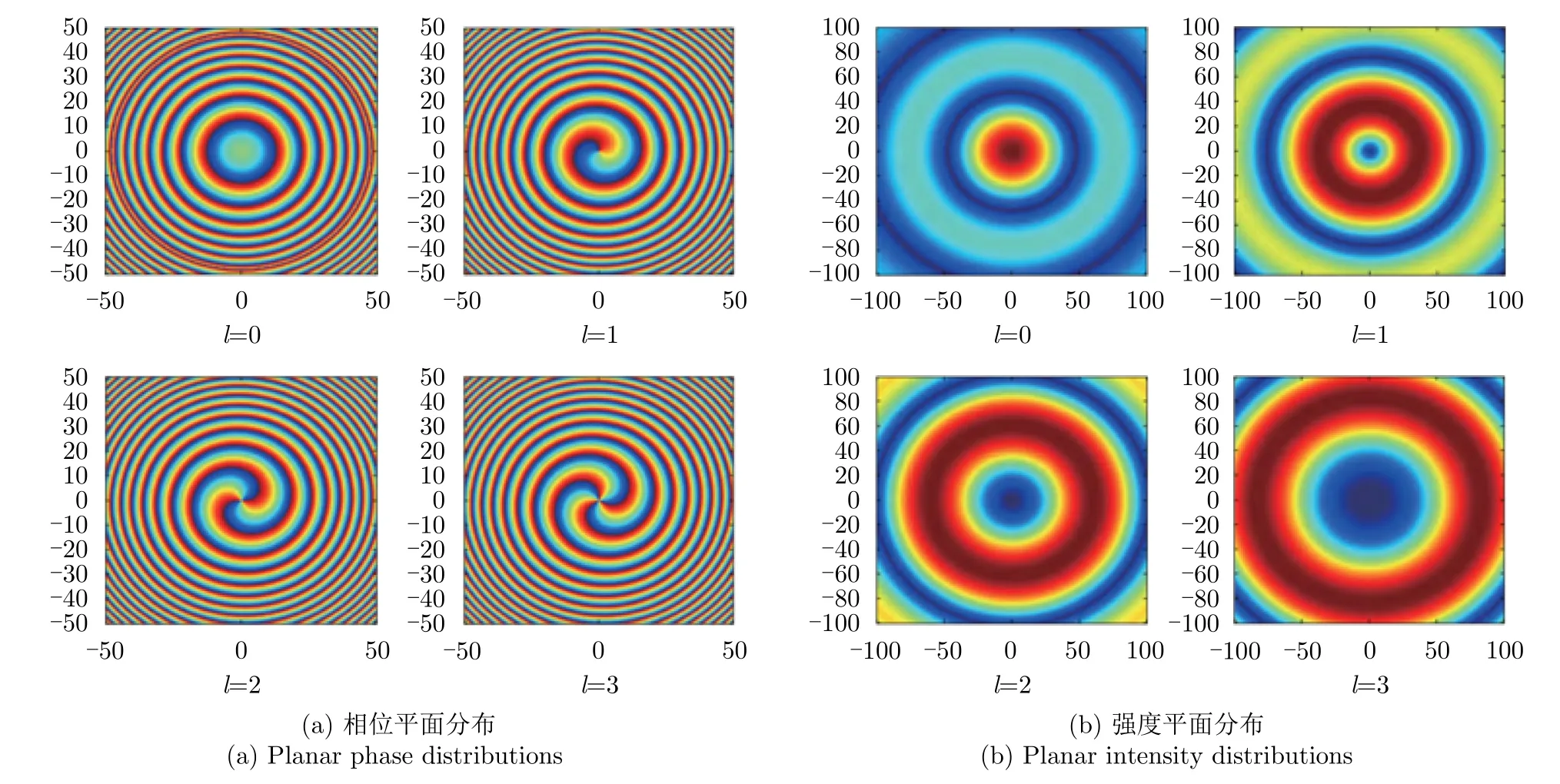
图1 不同OAM态的涡旋电磁波的相位和强度分布图[51]Fig.1 Phase and intensity distribution of vortex electromagnetic waves with different OAM states[51]

当l1和l2取整数时

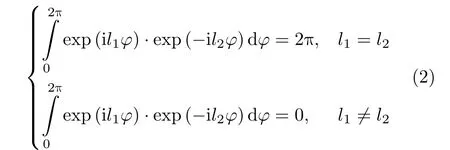
由式(2)可知，不同整数阶OAM态的涡旋电磁波之间相互正交，且理论上可以张成一个无穷维的希尔伯特空间。综上所述，涡旋电磁波不仅提供在波束内同距离不同方位角的目标的分辨力，而且不同整数OAM态的涡旋电磁波之间还相互正交，因此涡旋电磁波在雷达成像领域将具有非常大的应用潜力。

产生涡旋电磁波的主要天线结构通常可分为4类[25]，包括有源的单一微带贴片天线、行波天线、阵列天线和无源的超表面天线。单一微带贴片天线[22,52]具有结构简单、尺寸小和制作成本低的优势，因此在产生涡旋电磁波方面受到了研究者广泛的关注。行波天线[19,53]具有在宽带的范围内产生多种OAM模式的涡旋电磁波的优点，并且这一优点满足通信系统对扩大信道容量的需求，许多研究人员为了使系统更加实用化，在行波天线领域进行了许多的研究。阵列天线产生涡旋电磁波是目前发展较为成熟的一种方法[18,27]。相较于其他类型的天线而言，阵列天线的设计原理简单、结构灵活，并且可以通过改变输入的相位来轻松改变产生涡旋电磁波的模态。但阵列天线设计的难点在于其复杂的馈电网络，也有很多研究人员专注于这种阵列天线的馈电网络的设计和优化工作。超表面是由亚波长大小周期性排列的超材料共振器组成的，它通过改变共振器的形状和大小来实现调控电磁波的振幅或相位，通过在空间上合理地排列超表面结构，可以实现产生和调控涡旋电磁波[54-58]。相较于传统相控阵天线而言，超表面天线具有剖面低、馈电系统简单和易于波束成形等优点。但是超表面天线不仅需要庞大的阵列数量，还具有设计复杂以及体积笨重等缺陷，因此仍然需要对超表面天线进行优化和研究。

2.2 涡旋电磁波的成像原理

雷达成像通常是利用算法从回波信号中获得目标等效散射中心的分布信息，然而传统平面波和球面波的回波信号中包含的信息仅有目标的距离信息，并没有目标的方位角信息。因此传统雷达实现对目标在方位向的分辨依赖于雷达与目标之间发生相对运动，即依赖于距离多普勒原理实现目标在方位向的分辨。然而涡旋电磁波的相位不仅与距离有关，还与方位角有关，因此如果使用涡旋电磁波进行雷达成像，那么接收到的回波信号中不仅包含有目标的距离信息，还含有目标的方位角信息。

均匀圆形阵列(Uniform Circular Array,UCA)通过给阵元递增的相位来产生涡旋电磁波，因为其具有结构简单和产生涡旋电磁波的纯度较高等优势，所以常用UCA产生涡旋电磁波进行雷达成像。图2为使用UCA发射涡旋电磁波进行雷达成像的系统模型。使用UCA发送涡旋电磁波，然后位于UCA中心的天线接收回波信号，再通过算法处理回波信号，重建目标图像。

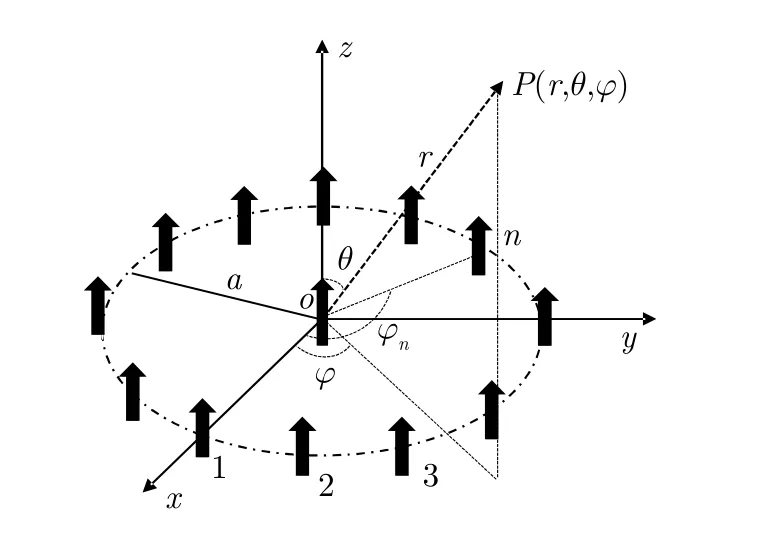
图2 均匀圆形阵列雷达模型Fig.2 Radar model of UCA

根据文献[32]，对于一个N阵元的UCA，给每一个阵元相同的激励，然后给第n个阵元加上附加相位Lφn,n=1,2,···,N，其中φn是第n个阵元的方位角，φn=2πn/N。UCA将会产生OAM态为L的涡旋电磁波，|L|＜N/2，并且产生的OAM态为L的涡旋电磁波在P(r,θ,φ)点的归一化电场表达式可以表示为

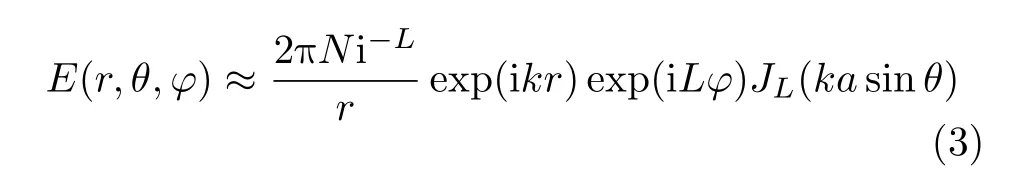
其中，k为电磁波的波数，k=2πf/c,f是电磁波的频率，c是光速；a是UCA的半径；JL(·)表示L阶的第1类贝塞尔函数。

若存在散射系数为σ的散射点P(r,θ,φ)位于成像空间中，那么接收到的回波信号可以表示为

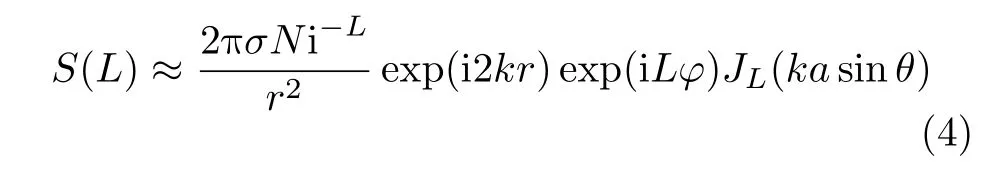
可以从式(4)中发现涡旋电磁波的OAM态L与目标的方位角φ存在近似的对偶关系，涡旋电磁波的频率f与目标的距离r也存在近似的对偶关系。因此可以通过不断地改变发送的涡旋电磁波的频率f和OAM态L，从而获得更多目标信息。图3为基于涡旋电磁波的雷达成像系统的信号处理原理图[59]，其中，发射信号采用频率步进信号(Stepped Frequency,SF)。由成像原理可知，回波采样数据在频率-拓扑荷域呈现二维矩形分布，因而通过二维傅里叶变换方法即可获取目标的距离-方位向位置信息。

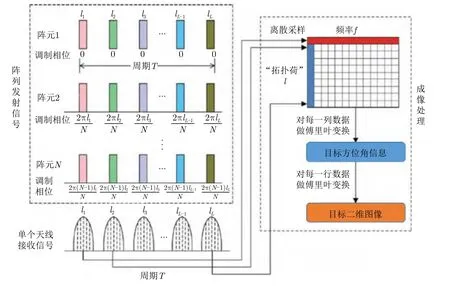
图3 涡旋雷达成像原理图[59]Fig.3 Schematic diagram for electromagnetic vortex wave imaging[59]

3 涡旋雷达成像技术

前面部分简要地介绍了涡旋电磁波及其成像原理，下文将对涡旋电磁波在成像方面的研究进行综述，主要包含涡旋雷达成像模型、涡旋雷达凝视成像算法、涡旋雷达运动成像3个方面。图4描述了涡旋电磁波在雷达成像领域的发展历程。

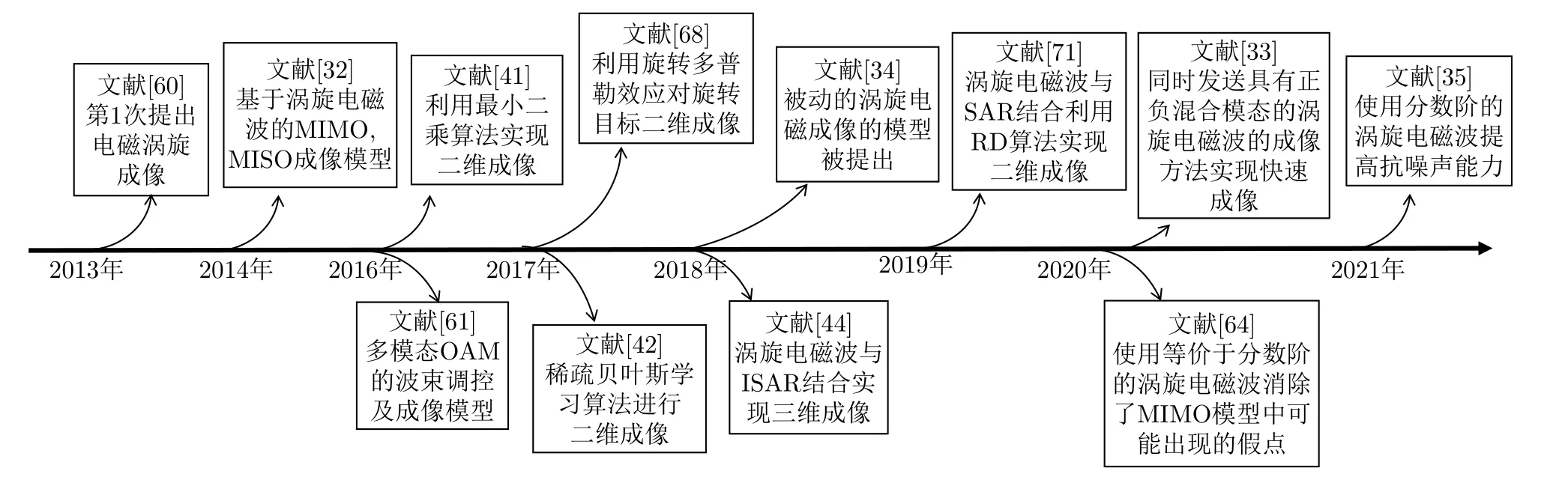
图4 涡旋电磁波在雷达成像领域中的发展历程Fig.4 The development history of vortex electromagnetic wave in the field of radar imaging

3.1 涡旋雷达成像模型

2013年，国防科技大学郭桂蓉等人[60]首次将涡旋电磁波应用到了雷达成像领域，使用的雷达成像模型为多输入多输出(Multiple In Multiple Out,MIMO)模型，MIMO模型的结构和仿真结果如图5(a)所示。其通过分析贝塞尔函数的频谱特性，指出涡旋电磁波的拓扑荷数与目标的方位角之间存在近似的对偶关系，并利用逆投影方法进行了信号处理，实现了对目标在方位向的一维成像，指出了涡旋电磁波对目标在方位向成像有巨大的潜力，为新体制雷达系统的发展提供了新思路。

2014年，国防科技大学刘康等人[32]建立了MIMO模型和多输入单输出(Multiple In Single Out,MISO)模型。MIMO模型是通过给UCA不同的OAM态的涡旋相位进而产生不同OAM态的涡旋电磁波，然后利用所有阵元接收回波信号，并给这些阵元加上与发送的涡旋电磁波相同OAM态的涡旋相位。基于N阵元的UCA，使用MIMO模型在方位向的分辨率ρφ=π/N。MISO模型是对MIMO模型的简化，在接收回波时不再使用UCA接收回波信号，而是使用一个位于UCA中心的天线接收回波信号。MISO模型的结构如图2所示。基于N阵元的UCA使用MISO模型在方位向的分辨率ρφ=2π/N。这两种模型在距离-方位向二维的仿真结果如图5(b)所示。比较基于MISO和MIMO模型的成像系统，MIMO模型要在发送端和接收端都给UCA附加上涡旋相位，而MISO模型仅在发送端给UCA附加上涡旋相位，因此基于MIMO模型发送OAM态为α的涡旋电磁波近似等价于基于MISO模型发送OAM态为2α的涡旋电磁波。也正是这种近似的双倍OAM态，使得近似发送的涡旋电磁波的OAM态为偶数，导致在成像结果上出现假点。

UCA产生不同模态的涡旋电磁波的主瓣方向不一样，导致成像质量受到影响。因此国防科技大学袁铁柱等人[61]提出使用同心圆环阵列产生涡旋电磁波的模型，不同的圆环产生不同OAM态的涡旋电磁波。由式(3)可知，UCA产生的涡旋电磁波的主瓣方向与UCA的半径a有关，因此可以通过改变圆环的半径a，从而调控产生的涡旋电磁波的主瓣方向，使发送的不同OAM态的涡旋电磁波的主瓣指向同一个方向。同心圆环阵列的模型和仿真结果如图5(c)所示，仿真结果表明：使用同心圆环阵列不仅能提高成像质量，还能提高抗噪声性能。进行雷达成像时，如果发送的电磁波的旁瓣幅度较高，不仅会造成能量的损失，还会因受非成像区域目标的影响而产生误差。为了降低UCA产生的涡旋电磁波的旁瓣幅度，国防科技大学秦玉亮等人[62]提出了在波束调控的同时实现旁瓣抑制的方法。这种方法使用的成像结构仍然是同心圆环阵列，仿真结果表明：这种方法的抗噪声能力更强，重建出的图像背景更纯净。同心圆环阵列使用多个圆环，这导致成像系统复杂。国防科技大学袁铁柱等人[63]基于相控阵原理提出了基于UCA的波束调控技术，从而使UCA产生的不同OAM态的涡旋电磁波的主瓣能指向同一方向。但是由于进行了波束调控导致产生的涡旋电磁波的纯度出现了恶化，成像模型如图2所示。仿真结果表明：即使基于UCA的波束调控技术产生的涡旋电磁波的纯度出现了恶化，但是该方法重建出来的目标图像依然优于直接使用UCA产生涡旋电磁波重建出来的目标图像。与基于UCA的波束调控技术相比，使用同心圆环阵列实现波束调控的技术仅仅依赖于改变每一个圆环的半径，而不需要改变每个阵元的激励，因此相对而言获得的涡旋电磁波的纯度更高。但是这种方法将导致系统的复杂度比基于UCA的波束调控技术要高，而且随着涡旋电磁波的OAM态的增大，为了实现波束调控其半径也会相应增大，导致天线的尺寸变大，实际应用十分困难。

图5 涡旋雷达成像模型Fig.5 Vortex radar imaging models

MIMO模型在方位向的回波信号以π为周期，导致基于MIMO模型的涡旋雷达成像在重建目标时会出现假点。南京理工大学樊振宏等人[64]针对该问题提出了等价于发送分数阶OAM态的涡旋成像方法，通过让接收回波时使用的OAM模式数α与发送的OAM模式数β之间存在α=β±1的关系，从而消除假点。仿真结果如图5(d)所示，表明仅使用整数阶OAM态的涡旋电磁波将会出现假点，而既使用整数阶又使用等价于分数阶的OAM态的涡旋电磁波能对目标图像准确重建。与基于MIMO模型的涡旋雷达成像相比，这种方法既可以获得更好的方位向分辨率ρφ=π/N，又不会出现假点。这种方法可以近似等价于在MISO模型中发送OAM态为α+β的涡旋电磁波，而且这种方法中α+β不仅可以是偶数，还可以是奇数，因此使用这种方法不会出现假点。文献[32]建立的MISO模型一次只能发送一种OAM态的涡旋电磁波，导致雷达成像效率不高。为此，国防科技大学刘红彦等人[33]提出了一种能同时发送正负OAM态的涡旋雷达成像方法，减少了一半的发送次数，大大地提高了成像效率，信号处理过程与仿真如图5(e)所示。尽管同时发送正负OAM态的涡旋雷达成像能提高成像效率，但是在使用较多OAM态的涡旋电磁波时，成像效率依然不高。国防科技大学刘康等人[34]提出了基于SIMO模型的被动涡旋雷达成像和小俯仰角下涡旋雷达成像，基于SIMO模型的被动涡旋雷达成像利用处于UCA中心的天线发送一个脉冲，然后使用UCA接收回波信号，并给UCA的所有阵元附加上不同OAM态的涡旋相位，实现通过发送一个脉冲等价于在MISO模型中发送多次不同OAM态的涡旋电磁波脉冲的效果。涡旋电磁波在小俯仰角上的辐射强度小，所以小俯仰角下涡旋雷达成像技术是通过对回波信号的包络进行关联，使得小俯仰角下的目标的回波信号增强。SIMO模型结构和仿真结果如图5(f)所示。仿真结果表明，SIMO模型可以通过发送一次脉冲实现二维成像，但是这种成像模型在方位向的分辨率仅是文献[32]建立的MIMO模型在方位向的分辨率的一半。与基于MIMO模型的涡旋雷达成像相比，基于SIMO模型的被动涡旋雷达成像可以近似地等价于在MIMO模型中使发送的涡旋电磁波的OAM态为0，然后改变用来接收的OAM态β，从而达到近似MISO模型的“逆过程”。

在方位向进行离散傅里叶变换(Discrete Fourier Transform,DFT)时，抗噪声能力与使用的OAM态的个数成正比[65]。国防科技大学刘红彦等人[35]提出使用分数阶OAM态的涡旋电磁波进行成像，通过使用UCA同时产生不同权重的不同OAM态的涡旋电磁波，实现等价于发送分数阶OAM态的涡旋电磁波的技术。仿真结果表明，当使用的OAM态α∈[-10,10]时，在Δα=1.0,0.5,0.2中，Δα=0.2表现出的抗噪声能力最强。表1给出了以上介绍的不同涡旋雷达成像模型对应的主要性能参数。

表1 已报道的涡旋雷达成像模型的性能Tab.1 Performance of reported vortex radar imaging models

涡旋雷达成像模型与涡旋雷达的成像效率以及方位向的分辨率息息相关，按照雷达成像的物理过程大致可以分为两个过程：第1个过程为电磁波达到目标；第2个过程为电磁波经过目标散射到达接收天线。因此，根据发送端的电磁波是否为涡旋电磁波和接收端是否使用UCA来接收回波信号可以大致将所有涡旋雷达成像模型分为3种：基于MIMO模型的涡旋雷达成像模型、基于MISO模型的涡旋雷达成像模型和基于SIMO模型的涡旋雷达成像模型。

3.2 涡旋雷达凝视成像算法

上述介绍的研究都是对涡旋雷达成像模型的研究，雷达成像的分辨率除了与成像模型有关之外还与处理回波信号的算法相关，使用不同的算法获得的成像精度不同并且利用的涡旋电磁波的性质也不尽相同。大致可分类为谱估计和稀疏恢复两大类算法，谱估计算法利用的性质是使用涡旋电磁波进行成像时目标的方位角与涡旋电磁波的OAM态近似成对偶关系。稀疏恢复算法利用的性质是不同OAM态的涡旋电磁波之间相互正交。接下来针对雷达与目标在整个成像过程中保持相对静止的场景下信号处理算法的研究进行综述。

2013年，国防科技大学郭桂蓉等人[60]利用方位角与OAM态之间近似的对偶关系使用逆投影算法实现了对单个目标和3个目标在方位向的一维成像，如图6(a)所示。2016年国防科技大学刘康等人[37]提出通过发送不同OAM态的线性调频的涡旋电磁波，然后对接收到的信号在时间域通过匹配滤波(又称为脉冲压缩)，最后在OAM域进行离散傅里叶变换，实现目标在距离-方位向的二维成像，仿真结果如图6(b)所示。随后该团队在2017年对涡旋电磁波的成像进行了实验验证[38]，使用UCA发送频率步进信号，每个频率都遍历所有的OAM态的涡旋电磁波，构建出如图3所示的二维矩阵，然后通过2FFT算法对目标成功进行了距离-方位向的二维重建。2020年，基于特征值分解的多信号分类(Multiple Signal Classification,MUSIC)算法被应用到涡旋雷达成像中[39]，实现了对目标在方位-俯仰向的二维成像，仿真结果如图6(c)所示。但是基于特征值分解的MUSIC算法需要知道成像区域的散射点个数并且计算量较大，所以北京理工大学闫晓鹏等人[40]提出了基于传播算子(Propagator Method,PM)算法的超分辨率成像，相比于MUSIC算法，PM算法的复杂度低且不需要知道成像区域散射点的个数就可以实现目标在方位向的一维成像，但是这个方法会使一个目标的成像结果对应于两个其真实位置偏移90°的谱峰，而不是真实目标的位置。因此需要对信号进行相位补偿，使得谱往右平移90°，从而得到分别对应于目标真实值和偏移180°的虚假谱。

因为当雷达工作于高频区时，成像目标的后向散射通常可以近似看成少数局部强散射源回波的叠加合成[66]。而高分辨雷达往往工作于高频区，因此高分辨雷达图像可看成稀疏信号。又因为不同的OAM态的涡旋电磁波之间相互正交，所以为如图3所示的回波矩阵提供了非相干性，因此可以在涡旋雷达成像中使用稀疏恢复类的算法。2016年，国防科技大学袁铁柱等人[41]通过发送步进频率的涡旋电磁波，建立了稀疏恢复模型，采用最小二乘算法进行恢复，并给出了在噪声时使用Tikhonov正则化方法的模型，仿真结果如图6(d)所示。2017年，国防科技大学刘康等人[42]将稀疏贝叶斯学习(Sparse Bayesian Learning,SBL)算法应用到涡旋雷达成像中，并给出了存在噪声、网格失配时增强稀疏贝叶斯学习(Enhanced Sparse Bayesian Learning,ESBL)算法和变分贝叶斯推理(Variational Bayes Inference,VBI)算法成像的结果，还通过实验验证了基于稀疏贝叶斯学习算法的距离-方位向的二维成像，仿真结果如图6(e)所示。仿真结果表明：增强稀疏贝叶斯学习算法和变分贝叶斯推理算法的抗噪声性能比稀疏贝叶斯学习算法强。2020年，上海交通大学王开志等人[43]基于正交匹配追踪(Dice Regularized Orthogonal Matching Pursuit,DROMP)法提出算法，实现了目标的二维成像，并且在保持低计算量的同时能够具有较好的抗噪声能力。

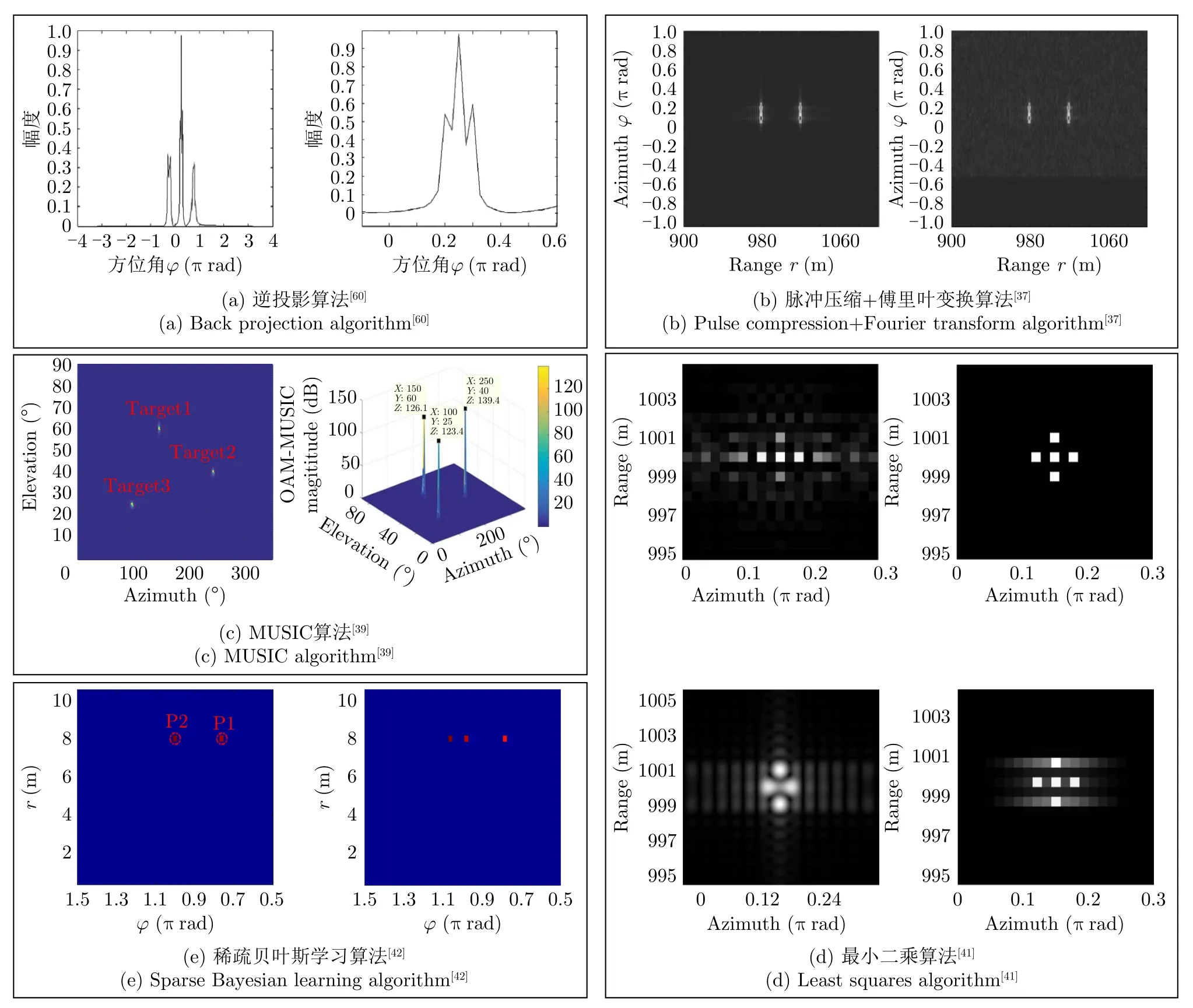
图6 凝视成像算法Fig.6 Gaze imaging algorithms

涡旋雷达凝视成像算法是对接收端接收到回波信号之后的信号处理的手段，通过其利用涡旋电磁波的不同特性，大致可分类为谱估计和稀疏恢复两大类算法。稀疏恢复类的算法虽然能够获得较高的分辨率，但是其要求发送步进频率的涡旋电磁波，这就使得稀疏恢复类算法将造成成像效率的降低和对天线特性要求的增加。而谱估计类的算法可以通过发送线性调频信号和使用基于SIMO模型的涡旋雷达成像模型实现快速成像。

3.3 涡旋雷达运动成像

上述综述的算法均是成像过程中雷达与目标保持相对静止的场景，然而实际在进行雷达成像时，为了获得更高的分辨率、更宽的成像区域或者对运动的目标进行成像，雷达与目标在整个成像过程中会发生相对运动，如SAR和ISAR。当雷达与目标发生相对运动时称为运动成像，接下来针对雷达与目标在整个成像过程中存在相对运动的场景的涡旋雷达成像模型与算法研究进行综述。

因使用涡旋电磁波对旋转物体进行雷达成像时会发生旋转多普勒效应[67]，国防科技大学刘康等人[68]对接收的回波信号中旋转多普勒效应和距离向的相位进行了补偿，实现了对旋转目标在方位向的一维成像，并通过实验验证了涡旋电磁波对旋转圆盘的成像，系统结构和成像仿真结果如图7(a)所示。中国科学院电子学研究所陈龙永等人[69]将传统SAR雷达系统与涡旋电磁波相结合，通过ωK算法实现对目标的二维成像，并通过实验比较了传统SAR生成的图像与发送涡旋电磁波的SAR生成的图像，实验结果表明：使用UCA发送的不是涡旋电磁波重建的图像质量低于发送涡旋电磁波重建的图像质量，系统结构和实验结果如图7(b)所示。但是该方法并未完全利用涡旋电磁波带来的关于目标的信息。2019年，内蒙古科技大学仝宗俊等人[70]提出了基于改进的反向投影(Back Project,BP)算法的涡旋电磁成像方法，使用的成像模型与文献[69]相同。在发送单个OAM态的涡旋电磁波的系统中，只需要在传统的BP算法的相位补偿后，增加一个方位调制函数，构成新的方位匹配滤波器用来补偿涡旋电磁波附加项对方位相位所产生的影响，就可以实现目标在距离-方位向的二维成像。在发送混合模态的涡旋电磁波系统中，成像算法只需要在单模态系统算法的距离向匹配滤波后进行方位包络补偿，即可实现二维成像。系统结构和仿真结果如图7(c)所示，仿真结果表明：单模态的涡旋雷达成像系统的方位向分辨率比传统SAR系统要好，且使用的OAM态的绝对值越大方位向的分辨率越高，多模态的涡旋雷达成像系统的旁瓣更低，多模态的成像质量比单模态的成像质量高。同年，国防科技大学刘康等人[71]提出了一种新的涡旋电磁波与SAR结合的方法，与文献[69]不同的是，发送的涡旋电磁波的OAM态是随慢时间的变化而变化的，之后在传统距离多普勒算法中增加了贝塞尔函数项的补偿和方位向的滤波，实现了对目标在距离向和横向的二维成像，系统结构和仿真结果如图7(d)所示。仿真结果表明：使用这种涡旋雷达成像与SAR结合的方法在方位向的分辨率比传统SAR在方位向的分辨率要高得多。

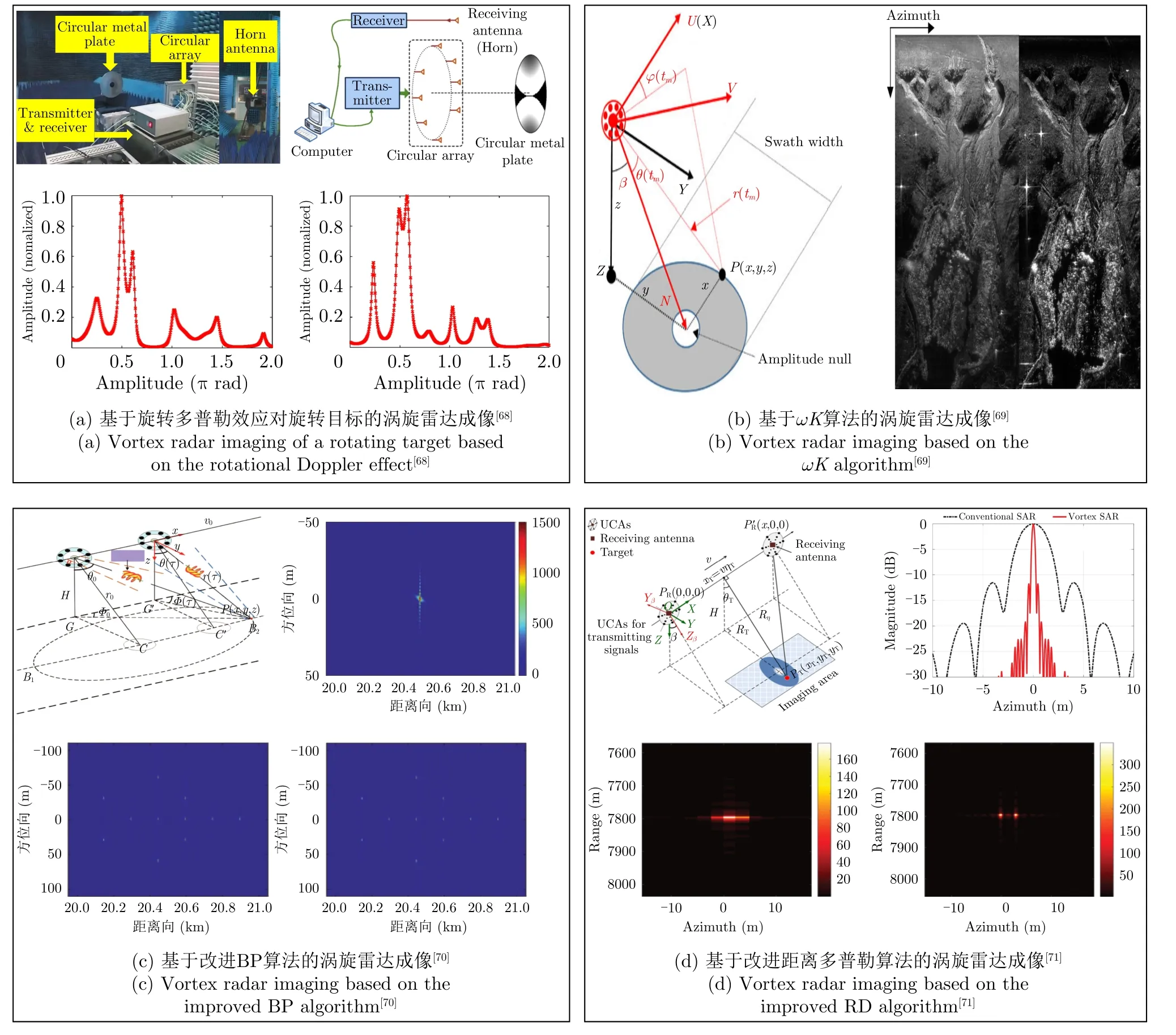
图7 一维和二维成像Fig.7 One-and two-dimensional imaging

2018年，国防科技大学刘康等人[44]首次将涡旋电磁波应用到ISAR当中，利用卷积反投影(Convolution Back Projection,CBP)和功率谱密度(Power Spectrum Density,PSD)估计结合的算法实现了对旋转目标的三维成像，系统结构和成像仿真结果如图8(a)所示。仿真结果表明：对目标图像进行重建时，用CBP和PSD估计结合的算法比使用FFT算法得到的图像背景更纯净。之后该团队又把涡旋电磁波引入条带合成孔径雷达(stripmap SAR)技术中[45]，与传统SAR不同的是，雷达发送的电磁波是涡旋电磁波，并且需要多次合成孔径，每次发送不同OAM态的涡旋电磁波，从而使得接收的回波信号具有3个维度，分别是慢时间、快时间和OAM态。通过把三维的回波信号分解为两个二维信号，进而分别求解出目标的一维和二维的图像，再通过几何关系合成为目标的三维图像，从而实现对目标的三维成像，系统结构和成像仿真结果如图8(b)所示。2020年，电子科技大学李中余等人[46]提出基于改进的距离多普勒算法的涡旋雷达成像方法，成像过程与文献[45]相似。在处理回波信号时，对三维信号在慢时间和快时间域使用距离多普勒算法，实现距离向和横向的分辨。然后通过滤波实现目标的横向信息与OAM态解耦，最后在OAM域进行FFT，从而实现目标的三维成像，系统结构和成像仿真结果如图8(c)所示。

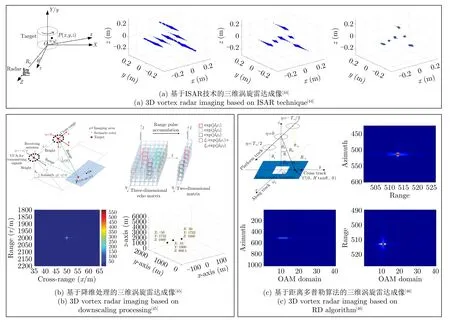
图8 三维成像Fig.8 3D imaging

以上研究表明：对旋转目标进行雷达成像除了使用ISAR技术之外，还可以利用涡旋电磁波的旋转多普勒效应实现对旋转目标的成像。当涡旋电磁波应用到SAR技术中时，这种发送涡旋电磁波的SAR的横向分辨率相比于传统SAR的横向分辨率有较好的提升。并且当涡旋电磁波应用到传统二维SAR和ISAR的成像模型中时，由于涡旋电磁波的OAM态理论上可以张成一个无穷维的希尔伯特空间，因此还可以实现对目标三维成像。

4 结论

本文主要针对如今涡旋电磁波在雷达成像领域的研究进行综述和总结。简要介绍了传统雷达存在的问题和涡旋雷达成像的起源；对涡旋电磁波的基本特性、产生方法和成像原理进行了介绍；紧接着对涡旋雷达成像模型、涡旋雷达凝视成像算法和涡旋雷达运动成像的研究进行了描述；继而在总结这些研究的基础上提出对今后研究的展望。

目前涡旋雷达成像技术还不够成熟，存在一些难以实际应用的问题。针对这些问题，提出一些可能的解决方案，总结如下：(1)目前使用的涡旋雷达成像的模型都是基于UCA的模型，而UCA产生大OAM态的涡旋电磁波需要的阵元数量较大，因此还需要设计具有小体积、低成本、高纯度的涡旋电磁波天线，以实现高分辨率的同时尽可能地减小系统复杂度。单一微带天线具有小体积、低成本等优势，因此可以建立以单一微带天线为收发天线的雷达成像模型，并推导出相应的数学模型，从而作为未来解决此类问题的潜在方案之一。(2)现有的研究考虑的噪声是理想的高斯白噪声，大多数的成像实验也是在理想条件下进行的，因此后续的研究应针对实际成像时存在的噪声特点、实际对目标成像时存在多次散射和强电磁干扰等对涡旋雷达成像产生较大影响的因素进行分析。针对噪声为非理想高斯白噪声的问题，可以通过寻找当前场景下相应噪声的特点，再设计相应的滤波器从而达到降噪的功能。(3)涡旋电磁波在小俯仰角下的强度几乎为零，这将会导致在进行雷达成像时无法对小俯仰角下的目标图像进行准确重建。为了应对这个问题，需要设计发散角更小的涡旋电磁波天线，从而减小无法成像的空域。或者利用相控阵原理对涡旋电磁波进行波束调控，使得波束在空域不断扫描，从而实现对目标图像的重建。超表面天线[58,72]既可以产生具有小发散角的涡旋电磁波又可以实现对涡旋电磁波进行波束调控，因此可以作为今后解决此类问题的潜在方案之一。平面涡旋电磁波(Plane Spiral Orbital Angular Momentum,PSOAM)可以由环形谐振腔缝隙天线产生[73]，PSOAM是将涡旋电磁波的发散角调整为90°时的涡旋电磁波，因此将PSOAM用于雷达成像不仅可以解决不同OAM态的主瓣方向不同的问题还可以解决由于涡旋电磁波的波束中空带来的问题。(4)当传输距离变远时，首先，涡旋电磁波随着传输距离的变远其涡旋电磁波的纯度将会降低，这导致对远距离目标成像时出现较大的误差。其次，涡旋电磁波还存在波束中空的问题，随着传输距离变远，将导致无法进行成像的空域越来越大。因此为了解决这些问题，需要设计能远距离传输、保持较高纯度且发散角小的涡旋电磁波天线。(5)需要设计更高分辨率、更低复杂度、更高成像效率的涡旋雷达成像模型和具有更高分辨率、更强抗噪声性能、更低复杂度的成像算法。

超材料技术在涡旋电磁波中的应用[74,75]和稀疏恢复类算法[42,43]的引入使得涡旋雷达成像技术在收发端和信号处理过程都将有可观的突破。随着涡旋雷达成像技术不断趋于完善，将为传统雷达存在问题的解决提供一个可行的方案，从而促进雷达的发展。