纯铂的热塑性变形行为及微观结构演变规律研究

许彦亭，王传军，谭志龙，王一晴，沈 月，闻 明，巢云秀，普志辉

(昆明贵金属研究所，贵研铂业股份有限公司 稀贵金属综合利用国家重点实验室，昆明 650106)

铂具有优良的化学性质，适中的强度、电导率、热导率和功函数，高延展性和易成膜等特性，能与半导体反应并形成稳定性化合物和金属型导电层，常应用于半导体和集成电路中[1]。纯铂靶材作为半导体和集成电路中溅射镀膜的原材料，通过对其微观组织的调控从而得到高质量的溅射薄膜是研究的热点。而材料的热加工工艺影响着材料的微观组织，故研究纯铂的热塑性变形行为，不仅可以较准确地描述变形温度、变形程度以及变形速率等工艺参数对其流变应力的影响规律，而且可以为纯铂靶材的加工工艺提供可靠的理论依据。

目前对纯铂的研究主要是关于强化机制及热处理过程中再结晶温度、晶粒尺寸和微观组织关联规律的研究，而对热压缩塑性行为的研究很少[2]。因此，本文主要开展纯铂的热塑性变形行为及微观组织演变规律研究，为纯铂靶材的热成形加工工艺的制定提供参考。

1 实验

以纯度(质量分数，下同)为99.99%的铂作为原料，通过拉拔工艺制备直径为6 mm的铂棒，并通过线切割制备长度为9 mm的圆柱试样。采用Gleeble-3500热模拟试验机进行热压缩实验，在压头与样品之间放置钽片并涂敷石墨膏以防止高温下压头与样品粘贴、减少摩擦力对实验数据的影响。设定升温速度为5℃/s，保温时间为3 min，实验真应变为0.9(工程应变为0.6)，热压缩工艺参数见表1，试验结束后样品进行淬火以保留其高温组织，获得纯铂真应力-真应变曲线。

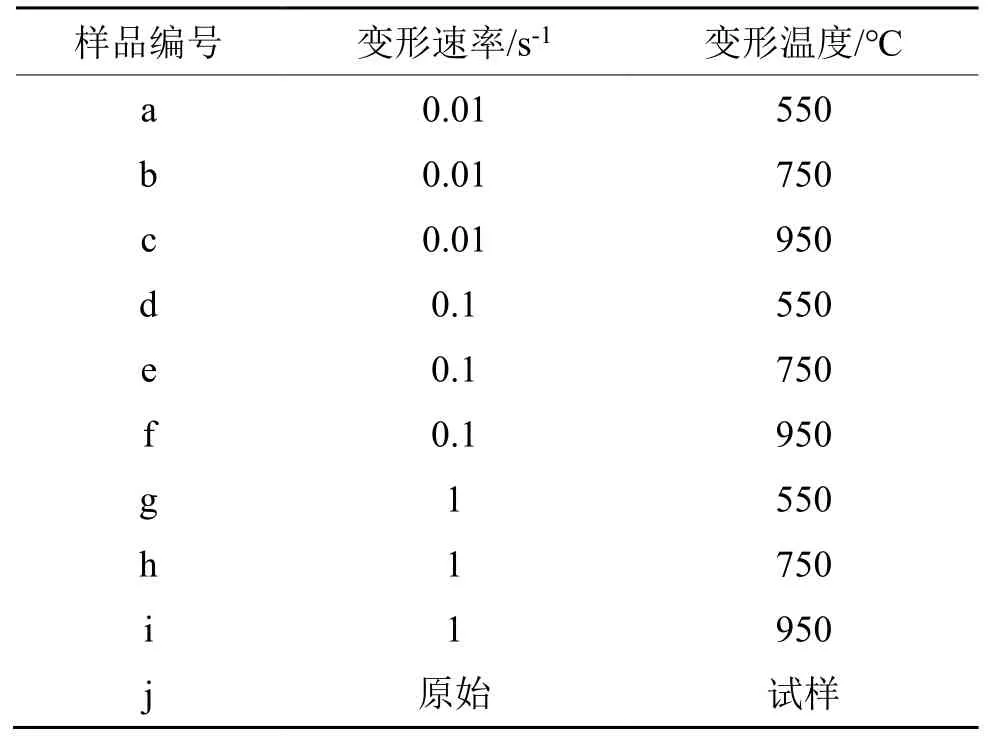
表1 纯铂热压缩工艺参数Tab.1 Technical parameter of hot compression experiment for pure Pt

本实验将进行热压缩实验后的铂样品沿纵向中轴线切开，取一半作为研究对象。选取纵剖面试样的中心位置，在40 mL饱和NaCl+10 mL HCl混合溶液中使用交流电进行电解腐蚀，并用金相显微镜(莱卡DM4000M)观察微观组织，用显微硬度仪(岛津HMV-FA2)测试材料显微硬度。

2 结果与讨论

2.1 纯铂真应力-真应变曲线

图1为纯铂在真应变为0.9、不同热压缩工艺条件下获得的真应力-真应变曲线。

图1 纯铂真应力-真应变曲线Fig.1 True stress−true strain curve of pure Pt

该过程由热变形过程中位错增值和积累发生的加工硬化及动态回复和再结晶的软化共同作用决定。在变形初始阶段，流变应力随应变量增大而增大，且斜率逐渐降低，应力升高到极限值后达到稳定态。应力应变曲线呈波浪状变化说明动态回复和再结晶与加工硬化、位错增殖交替进行，样品在热压缩过程中发生了不连续动态回复和再结晶。在应变速率一定时，流变应力随温度升高而降低，在变形温度一定时，流变应力随应变速率的升高而增大。

观察曲线在应变速率0.01 s-1、变形温度750℃、950℃和应变速率0.1 s-1、变形温度950℃的真应力－真应变曲线出现了明显的峰值，而应变速率1 s-1、变形温度950℃时的真应力应变曲线出现不太明显的峰值，表明这些热压缩工艺条件下以动态再结晶为主，而其余变形条件下主要是动态回复为主。这是由于纯铂具有较高的层错能[3]，其位错的攀移和交滑移过程容易进行，一般情况下动态回复就能完全消除加工硬化，因而其高温变形的主要软化机制为动态回复。而在较低应变速率变形时，变形时间充足，变形储能较大，位错运动的较充分，容易发生动态再结晶；在温度较高时原子运动加剧，位错运动阻力减小，变形过程中的变形储能增加，再结晶形核率、晶核长大的驱动力就越大，也容易发生动态再结晶，即高形变温度和低应变速率有利于纯铂动态再结晶的发生。故本实验中真应力-真应变曲线在高温950℃、3个应变速率和低应变速率为0.01 s-1、温度为750℃的热压缩条件呈现再结晶特征。

2.2 纯铂热变形本构方程的建立

由图1纯铂真应力-真应变曲线可知，热塑性变形下纯铂高温流变应力与变形温度和变形速率相关。其关系式可由Sellars等[4]提出的包含变形激活能Q、变形温度T、变形速率έ和流变应力σ的双曲线正弦形式的修正Arrhenius公式来表示：

其中在低应力时(ασ＜0.8)时，(1)式可近似于(2)式的指数关系，在高应力时(ασ>0.8)时，(1)式可近似于(3)式的幂数关系，(1)式适用于所有应力水平。

上式中A、α、n、β、Q、A1、A2均为材料常数，α=β/n为应力水平常数，R为气体常数，值为8.314 J/(mol·K)。分别对式(1)、(2)、(3)两边取对数，并假设变形激活能Q是与变形温度T无关的常数。

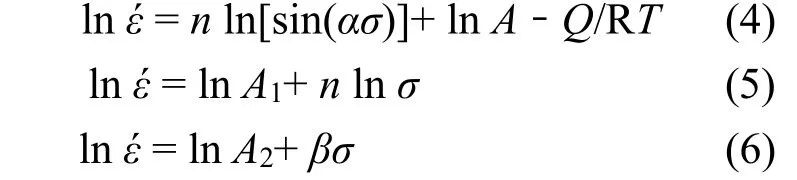
将不同热压缩工艺条件下纯铂热变形实测峰值应力带入式(5)、(6)，利用Origin线性拟合绘制出lnέ-lnσ和lnέ-σ的关系图，如图2所示。

图2 纯铂不同变形温度下峰值应力(σ)与应变速率(έ)的关系Fig.2 Relationship between peak stress (σ) and strain rate (έ) of pure Pt at different deformation temperatures

根据拟合的结果，可求出n和β的值，其大小分别为图2(a)和图2(b)中3条直线斜率的平均值：n=12.2和β=0.089，由此求出α=β/n=0.0073。再将α代入(4)式绘制出ln έ – ln [sinh (ασ)]的关系图，如图3所示。

图3 纯铂在不同变形温度下ln έ与ln [sinh (ασ)]的关系Fig.3 Relationship between Inέ and In[sinh (ασ)] of pure Pt at different deformation temperatures

图3斜率的平均值为8.74，此时各个变形速度的相关系数均在0.997以上，也能说明双曲正弦函数关系的回归效果是较好的，可以用此式计算相应条件的流变应力。

对(4)式变形可得：

绘制出ln [sinh(ασ)]-1/T的关系图，如图4所示。此时斜率的平均值为3014.68，带入(8)式得Q=219.06 kJ/mol。对(1)式变形可得并赋值为Z：

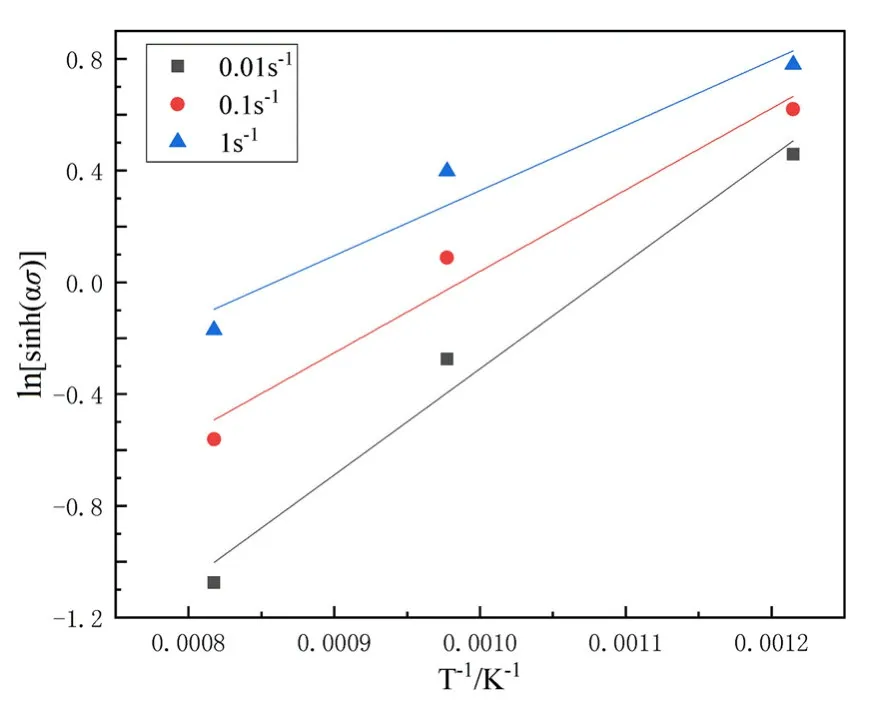
图4 纯铂在不同变形速率下ln[sinh(ασ)]与温度的关系Fig.4 Relationship between ln[sinh(ασ)] and temperature of pure Pt at different strain rates

此时Z有实际特殊意义，称为Zener-Hollomon参数[5]。它是温度补偿的变形速率因子，反映了金属热变形的难易程度，是热变形过程中一个重要的参数。对式(9)两边取对数得：

将热变形激活能Q代入式(10)，绘制出lnZ- ln[sinh(ασ)]的关系曲线，如图5所示。直线斜率为n=7.98，截距为lnA=23.90。

图5 ln Z-ln [sinh(ασ)]的关系Fig.5 Relationship between ln Z and ln [sinh(ασ)]

将此时的n重新代入α=β/n，计算得到新的激活能Q。再用之前的方法，重新迭代计算n值，直到n值标准差最小，由此得出的材料常数A、n、α、Q更准确[6]。此时A=2.32×107、n=5.48、α=0.014、Q=208.51 kJ/mol，则：

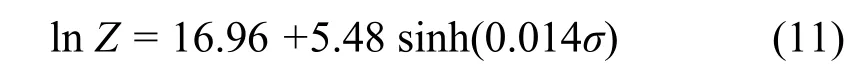
将所求的材料常数A、n、α、Q代入式(9)，可求出所有应力状态的流变应力本构方程：

将式(12)变换可得：

由式(13)可得出纯铂在不同热压缩变形条件下的拟合公式计算值，与实验值进行对比见图6。

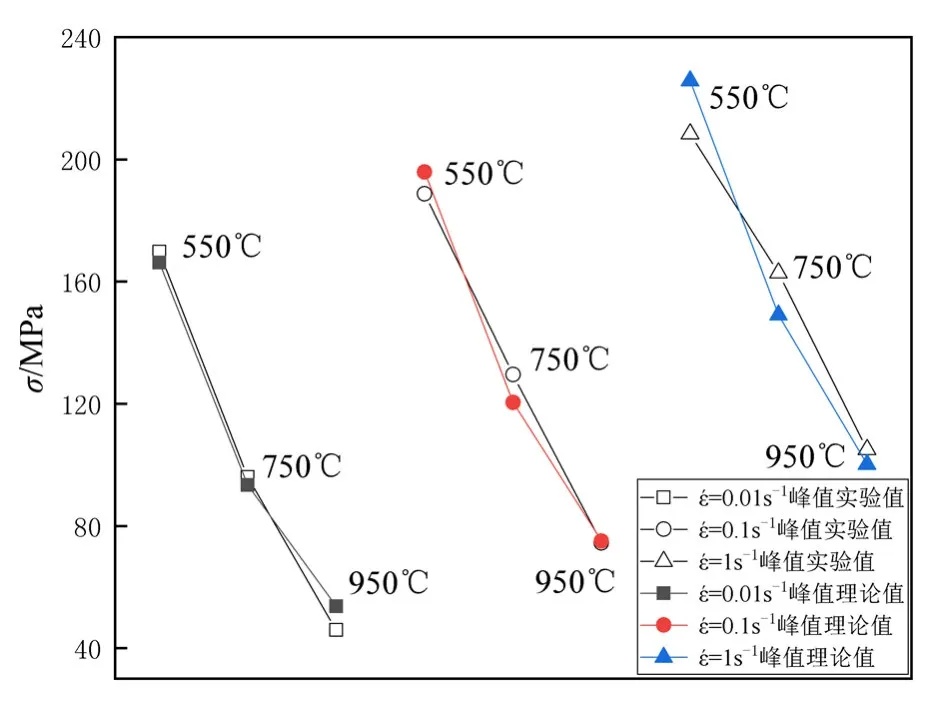
图6 纯铂在不同热压缩变形条件下的理论与实验峰值Fig.6 Theoretical and experimental values of peak stress at different hot compression condition

除变形温度为950℃、应变速率为0.01s−1时的相对误差是14.5%，其他热压缩变形条件下的相对误差绝对值均在9.25%以下，平均相对误差是5.9%，该方程能较好的预测纯铂热塑性变形行为。

2.3 显微组织观察

图7为真应变为0.9的纯铂在不同热压缩工艺条件下的金相图片。

图7 纯铂在不同热压缩工艺条件下金相图片Fig.7 The metallograph of pure Pt at different hot compression conditions

未进行热压缩试验的样品图(j)为沿拉拔方向拉长的晶粒(晶粒平行于热压缩力施加方向)，经过热压缩试验后，原始晶粒全部消失，所有样品微观组织方向变为向垂直压缩方向延展。热压缩试验过程中纯铂发生了动态回复和再结晶。图(d)(e)(g)(h)即在其应变速率έ=0.1 s-1和έ=1 s-1时、变形温度550℃和750℃的金相组织中未观察到明显再结晶形核，原始样品的组织基本消失，此时动态回复机制主导着材料的热压缩变形过程。应变速率έ=0.01 s-1时下，图7(a)中550℃热压缩条件下样品能观察到细小的再结晶形核晶粒，但仍然由动态回复机制主导着材料的热压缩变形过程。图7(b)中750℃时能观察到再结晶和晶粒的长大，而在图7(c)、(f)、(i)中，高温950℃、3个变形速率下样品均发生了明显的再结晶和晶粒长大现象，变速率为1 s-1, 0.1 s-1和0.01 s-1时，平均晶粒尺寸分别为84.94、115.30和296.64 μm，随应变速率的减小，晶粒有足够的时间长大，再结晶晶粒尺寸变大，随温度的升高，再结晶晶粒尺寸变大，此时动态再结晶机制主导着材料的热压缩变形过程。这是由于纯铂具有较高的层错能，其滑移面上不全位错间的层错带(扩展位错)较宽，相距较远的不全位错很难聚成全位错，因而位错的交滑移和攀移困难，动态回复难以同步抵消形变时位错的增殖积累[7]，当变形温度较高时有足够的储存能、变形速率较低时会有足够的时间诱发再结晶形核和长大，导致此时动态再结晶机制会主导着材料的热压缩变形过程，这些与真应力应变曲线呈现的规律是一致的。

2.4 显微硬度

图8为真应变为0.9的纯铂在不同热压缩工艺条件的显微硬度。

图8 纯铂在不同热压缩工艺条件显微硬度Fig.8 Microhardness of pure Pt at different hot compression conditions

原始试样由拉拔工艺获得，有较大的变形量，内部位错堆积多，硬度较高，而动态回复和再结晶造成的软化使热压缩试验后的样品硬度降低。在变形速率一定时，硬度随变形温度升高而减小，因为温度越高，加快了回复过程中的位错对消和重新排列过程，并促进再结晶形核率、晶核长大的驱动力也越大，软化作用较明显，故硬度降低。当变形温度一定时，硬度随变形速率升高而升高，变形速率越大，容易形成高密度位错，却没有足够的时间进行动态回复和再结晶软化，故硬度较高。

与2.3节样品的微观组织联系，在变形速率为0.01 s-1下变形温度为750℃和3个变形速率下变形温度为950℃时材料发生了动态再结晶，这些情况下样品硬度降低明显，这是由于动态回复阶段主要是位错偶对消、胞壁多边化而形成亚晶以及亚晶合并过程，不涉及大角度晶界的迁移，不会形成新的再结晶晶粒，但会发生多边化而形成亚晶，而动态再结晶涉及大角度晶界的迁移再结晶晶粒的生成对样品的软化作用较明显[7]。且从显微硬度的图中可以看出变形速率为0.01 s-1时的硬度值波动是最小的，此时在低应变速率下样品有足够的时间均匀化组织，故硬度值也比较均匀。

2.5 分析和讨论

本文热加工实验后的样品微观结构与文献[1]中冷轧退火后的微观结构相比，发现高温和保温时间有利于再结晶和再结晶晶粒长大的发生。由于铂具有较高的层错能，在文献[2]中再结晶和晶粒长大的微观结构中仅出现极少量的孪晶，在本文950℃热加工试验后再结晶和晶粒长大的微观组织结构(图7(c)、(f)、(i))中未发现孪晶结构，这是由于高层错能的金属不易产生栾晶且随着温度的升高，层错能升高，出现的孪生可能性就更小了。

文献[1-2]中给出退火态纯铂的显微硬度为40左右，小于本文中在950℃各应变速率下60左右的硬度值，主要是由于在热压缩试验中高温造成的动态回复和再结晶对铂的软化作用还不足以抵消热加工造成的加工硬化。

3 结论

1) 纯铂流变应力随变形温度的升高和应变速率的降低而降低，其热压缩变形过程中软化行为是在变形温度和变形速率的共同作用下决定的，一般以动态回复为主；而在低应变速率和高形变温度下以动态再结晶为主。

2) 采用Zener-Hollomon参数方程拟合塑性变形流变应力本构方程，得到纯铂的热变形激活能为Q=208.51 kJ/mol，流变应力拟合公式计算值与实验值的平均误差为5.9%，其流变应力本构方程变形可得正文中式(13)的形式。

3) 纯铂在进行热压缩实验后，动态回复和再结晶的发生使材料硬度降低，而动态再结晶的发生使硬度明显下降，低变形速率下微观组织比较均匀，此时的硬度值波动也较小。