线控四轮独立转向汽车执行机构容错控制研究
2021-11-06何友国耿朋杰蔡英凤袁朝春
何友国,耿朋杰,蔡英凤,袁朝春
(江苏大学 汽车工程研究院,江苏 镇江 212013)
随着智能车的发展,汽车电子元件大规模应用的趋势越来越明显。线控加速、线控制动和线控转向等技术在汽车上得到了广泛关注[1]。线控转向系统是汽车上的一个电控系统,它取消了方向盘和车轮之间的机械连接,取而代之的是执行电子指令的电控执行机构。与传统的转向系统相比,线控转向系统采用可变转向比,通过减少转向操作,减轻驾驶员的驾驶负担。通过对转向执行机构电机的主动控制,可以提高转向的安全性。取消方向盘和前轮之间的机械连接可以提高碰撞安全性[2-4]。但由于线控转向系统在转向盘和转向轮之间不存在机械连接,转向执行机构频繁工作,电子设备的鲁棒性比传统机械、液压部件低,电子部件很容易随时出现各种故障。执行机构发生故障时,可能无法提供预期的扭矩,从而危及车辆的运动控制,导致线控转向系统性能不理想[5-6]。线控四轮独立转向汽车通过4个电机分别控制4个车轮的转向运动,执行机构协调执行指令,可能会出现部分失效、中断及卡死故障。因此,设计出即使在执行机构发生故障时也能保持必要的车辆性能的容错系统是十分必要的。典型的容错方法分为硬件冗余和解析冗余[7-10]。
相关研究更多采用硬件冗余方式[11-12],如采用双转向电机和多转向电机、多传感器和多控制器,实现硬件备份。重庆大学李小鹏进行了线控前轮转向汽车的传感器故障容错研究[13]。李春善等对线控四轮驱动汽车的驱动失效进行容错研究,取得较好效果[14]。陈旭芳等对四轮驱动的执行器失效进行了容错研究,设计状态反馈控制器,实现车辆稳定性控制[15]。现有文献多基于车辆传感器故障和驱动系统执行器进行容错研究,较少涉及线控转向执行器容错控制研究,且以上研究都存在由于硬件冗余而增加组件使得整个线控驱动系统的成本过高的问题。对具有多执行器的四轮独立转向汽车而言,高成本或者物理空间受限等,很难使系统利用硬件冗余而实现故障容错。主动容错中的解析冗余由于利用系统中的不同部件在功能上的冗余性来实现故障容错受到了广泛关注。
因此,考虑到线控四轮独立转向汽车的转向执行机构在使用过程中可能会出现部分失效、中断和卡死等多种常见故障情况,本文将文献[16]中的直接自适应算法拓展到线控四轮独立转向汽车系统中。考虑转向系统执行器非参数化时变卡死和一直存在的时变扰动,在车辆2自由度动力学模型基础上,以跟踪参考模型为目标进行了容错控制器的设计,实现执行器故障模式下汽车对理想参考模型的零质心侧偏角和修正横摆角速度的跟踪。基于Lyapunov理论,可以保证所得到的系统渐进稳定。
1 整车和执行机构故障建模
1.1 整车动力学模型
针对四轮独立转向汽车侧向动力学的研究,建立四轮独立转向车辆的整车2自由度模型,忽略车辆侧倾的影响,只考虑侧向和横摆2个自由度,整车2自由度模型如图 1 所示。
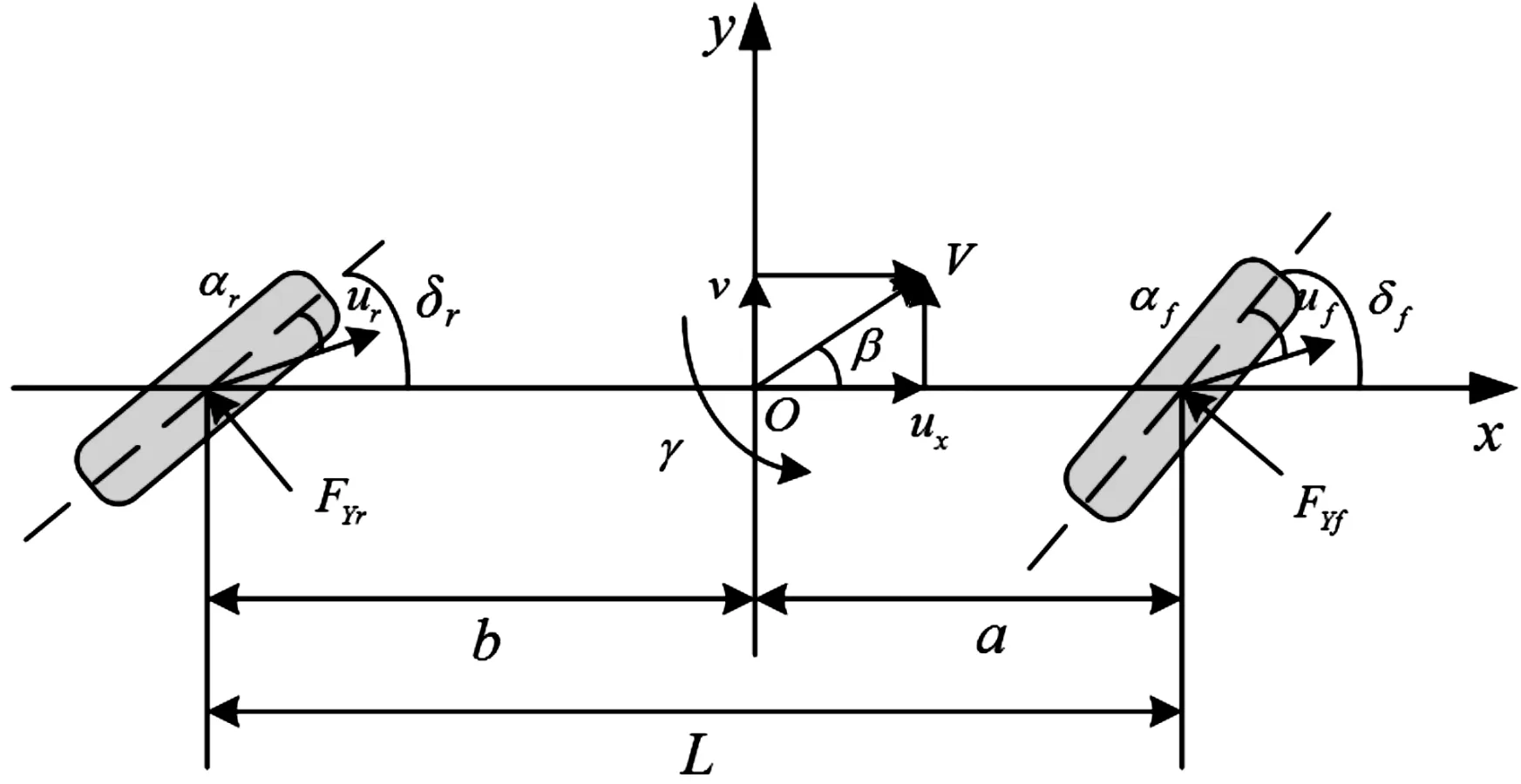
图1 4WS的2自由度模型示意图
图1中,FYf和FYr分别是前后轮侧向力;β是质心侧偏角;γ是横摆角速度;m是车辆质量;V是车辆的行驶速度;a是质心到前轴的距离;b是质心到后轴的距离;δf和δr是分别是前、后轮转角。
假设汽车关于车轴中心垂直面左右对称;忽略悬架的作用,认为汽车只作平行于地面的平面运动;忽略左右车轮轮胎由于载荷变化而引起的轮胎特性的变化;认为左右车轮侧偏角相同并统称为前轮侧偏角或后轮侧偏角。基于以上假设[17],根据牛顿第二定律,可以得到以下运动学方程:
侧向运动:
(1)
横摆运动:
(2)
其中Iz是汽车绕z轴的转动惯量。基于对轮胎侧偏特性的考虑,采用如下的近似线性模型:
FFf=-Cfαf,FFr=-Crαr
(3)
其中:Cf是前轮的侧偏刚度;Cr是后轮的侧偏刚度。
车轮的侧偏角定义如下:
(4)
将式(4)代入式(3),根据系统运动方程(1)和(2)可得:
(5)
式(5)可写成如下标准的状态空间方程形式:
(6)
其中:x(t)=[βγ]T是状态向量;u(t)=[δfδr]T是控制输入量;A0∈R2×2是系统矩阵;B0∈R2×2是输入矩阵,对应的有:
将4WS系统的2自由度车辆动力学模型修正为4WIS模式[18],以4个车轮转角作为控制器输入,如图2所示。

图2 4WIS的2自由度模型示意图
可得到如下标准的状态空间方程形式:
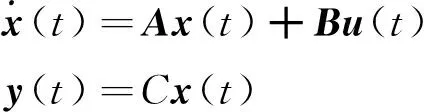
(7)
其中:x(t)=[βγ]T和u(t)=[δflδfrδrlδrr]T分别为状态向量和控制输入量;A∈R2×2是系统矩阵;B∈R2×4是输入矩阵,对应的有:
1.2 参考模型
车辆质心侧偏角和横摆角速度是作为表征车辆操纵稳定性的重要指标,因此4WIS控制系统的理想参考模型应包含这2个特征量,根据已有文献分析,车辆质心侧偏角应当越小越好[18]。线性2自由度模型可以在一定范围内很好地描述车辆的转向运动,同时大多数人更习惯于FWS汽车的转向特性,因此在质心侧偏角较小的情况下,可以将FWS汽车线性2自由度模型的横摆角速度稳态值视为理想的横摆角速度。
将理想横摆角速度修正为:
(8)
利用零质心侧偏角作为质心侧偏角的理想参考目标,式(8)描述的横摆角速度作为理想参考目标,将理想质心侧偏角和横摆角速度写成以下状态空间方程形式:
(9)
式中:
式中τβ、τγ分别表示质心侧偏角与横摆角速度的惯性环节时间常数均取值为0.1[18-19]。γ*同时需要满足路面附着系数的限制,即要满足式(8)。
1.3 执行器故障模型
由于长期频繁处于执行控制任务状态,执行器是最容易发生故障的环节,在系统的容错控制设计中,对执行器采用适当的容错控制策略显得异常关键。本部分所考虑的线控四轮转向汽车执行机构具有4个执行器。执行器具体常见故障类型包括部分失效、中断和卡死故障。
考虑以下线性时不变连续时间系统状态方程:
(10)
根据所建立的2自由度模型,式中x(t)∈R2×1表示状态,u(t)∈R4×1为控制输入,考虑ω(t)∈R1×1表示扰动的连续向量方程。A、B1、B2表示已知的具有适当维数的常数矩阵。
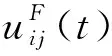
为了对所有这些故障类型进行通用建模,定义以下执行器故障模型[20-21]:
(11)


(12)
各种故障模式的具体情况如表1所示。
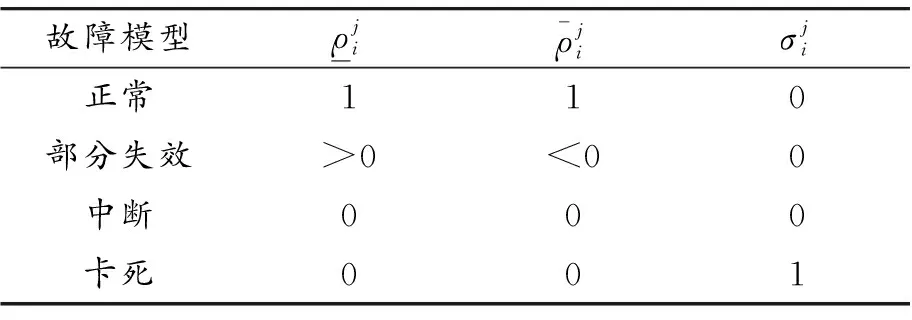
表1 故障模型
定义:
(13)
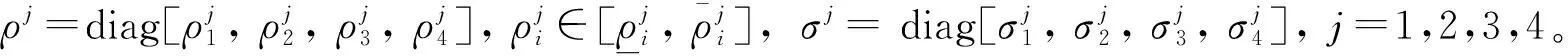
uF(t)=ρu(t)+σus(t)
(14)
其中ρ=diag[ρ1,ρ2,ρ3,ρ4]∈{ρ1,ρ2,ρ3,ρ4}。
带有执行器故障(14)的系统(10)可以表示为:
(15)
为保证在状态反馈设计中能达到容错目的,以下假设在容错控制系统中成立:
假设1所有系统的状态可测。

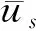
假设4对系统(15),存在一个恰当维数的矩阵方程F使得:
B1=B2F
(16)
假设5对所有执行器故障模式ρ∈{ρ1,ρ2,ρ3,ρ4}满足:
rank[B2ρ]=rank[B2]
2 直接自适应容错控制器设计
设计自适应率直接估计控制器参数,并且提出一个自适应控制增益方程补偿执行器故障和扰动。在不需要知道执行器故障和扰动边界信息的情况下,使所得到的闭环系统渐近稳定。
定义跟踪误差为
(17)
根据式(17),有
(18)
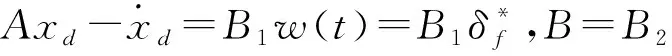
(19)
考虑线性时不变容错控制系统模型和以下结构控制器:
(20)
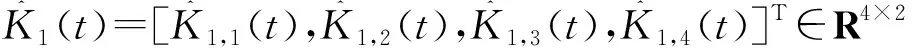

(21)

(22)
其中a1,b1是合理的正常数,满足:
(23)

(24)

由此,根据式(16)(20)和假设(4),闭环容错控制系统模型可以写成:
B2σus(t)+B2Fw(t)
(25)
令:
(26)
由于K1,i、k3为未知常数,可以有以下误差系统:
(27)

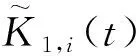
证明:对自适应闭环系统(25)定义一个Lyapunov函数如下:
(28)

2xTPB2ρK2+2xTPB2σus+2eTPB2Fω+
(29)
根据不等式(37)和假设3,式(29)可写成:
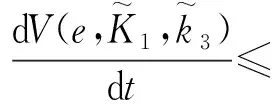
(30)
由假设2可知,(A,B2)可稳,存在常数K∈R4×2和P∈R2×4,使得
(31)
条件rank[B2ρ(t)]=rank[B2]保证B2列的线性组合可以被B2ρ(t)中的列重组,即存在一个K1使得:
B2ρK1=B2K
(32)
对任何ρ(t)∈Δρj。由此,对任何ρ(t)∈Δρj,存在一个K1满足:
(A+B2ρK1)TP+P(A+B2ρK1)<0
(33)

(34)
定义:
Q=(A+B2ρK1)TP+P(A+B2ρK1)
(35)
则由(30)使得:
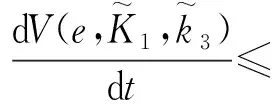
(36)
3 仿真分析

Okubo和Kamiya介绍了Jordan李代数,其与李代数和Jordan超代数密切相关[1]。文献[2]证明了Jordan李代数的Engel定理及Cartan子代数的性质。2006年,Hartwig等[3]研究了李代数的某种形变Hom李代数。目前,Hom李代数的表示[4]、二次Hom李代数[5]的研究已经取得了一些成果,并进一步把Hom李代数的某些成果推广到Hom李超代数[6]和Hom李色代数[7]。作为Hom李代数的推广,文献[8-9]研究了Hom-Jordan李(超)代数,并讨论了其表示,得到了其T*-扩张的结构。本文研究Hom-Jordan李代数的交换扩张和交换扩张的等价。
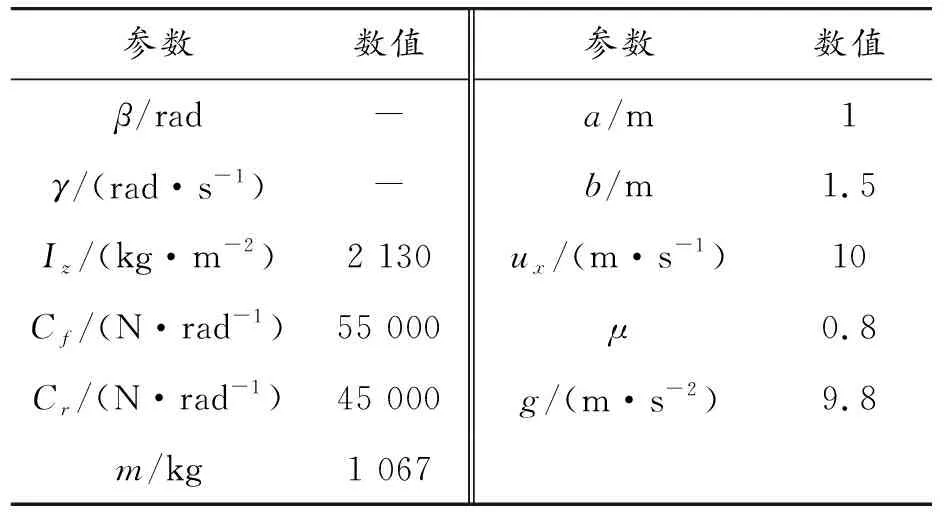
表2 车辆参数
仿真初始条件如下:
a1=1,b1=10,c1=50,x(0)=[0.8 0.3]T
Γi=diag[10 10 10 10]
k3(0)=0,i=1,2,3,4,
为了验证所设计控制器的有效性,设置以下不同仿真工况:
1) 第1种工况:t<4 s各执行器处于正常状态;t=4 s第3个执行器出现中断故障,描述为ρ=diag[1 1 0 1],t=8 s第1个执行器出现时变卡死故障,第2、3、4个执行器均失效50%,其中,时变卡死故障描述为us1=1+sin(0.5*t)。
2) 第2种工况:t<4 s各执行器处于正常状态;t=4 s第3个执行器出现中断故障,无控制。
图3、4表示在第1种故障情况下的系统状态量质心侧偏角和横摆角速度跟踪误差响应曲线。由图可知,在t=4 s时,第3个执行器发生中断故障时,车辆的质心侧偏角和横摆角速度均发生较大波动,车辆处于失稳状态,经过控制器的持续调节,并在3 s时间内快速恢复到跟踪理想值,误差逐渐趋向于零;t=8 s时第1个执行器出现时变卡死故障,第2、3、4个执行器失效50%,在此种复杂工况下,质心侧偏角和横摆角速度依然能被控制在较小范围波动,并在3 s时间内恢复稳定状态,跟踪误差逐渐趋向于零。作为对比,图5、6是在第2种工况下的仿真结果,可以看出在t=4 s出现故障的情况下,无控制时,系统的状态量发生剧烈的变化,这将严重威胁到驾乘人员的安全。因此,由仿真结果可以得出,所设计的容错控制器在线控四轮独立转向汽车执行器发生故障时依然可以使线控四轮独立转向汽车很好地跟踪参考模型,能够有效保证汽车的稳定性。
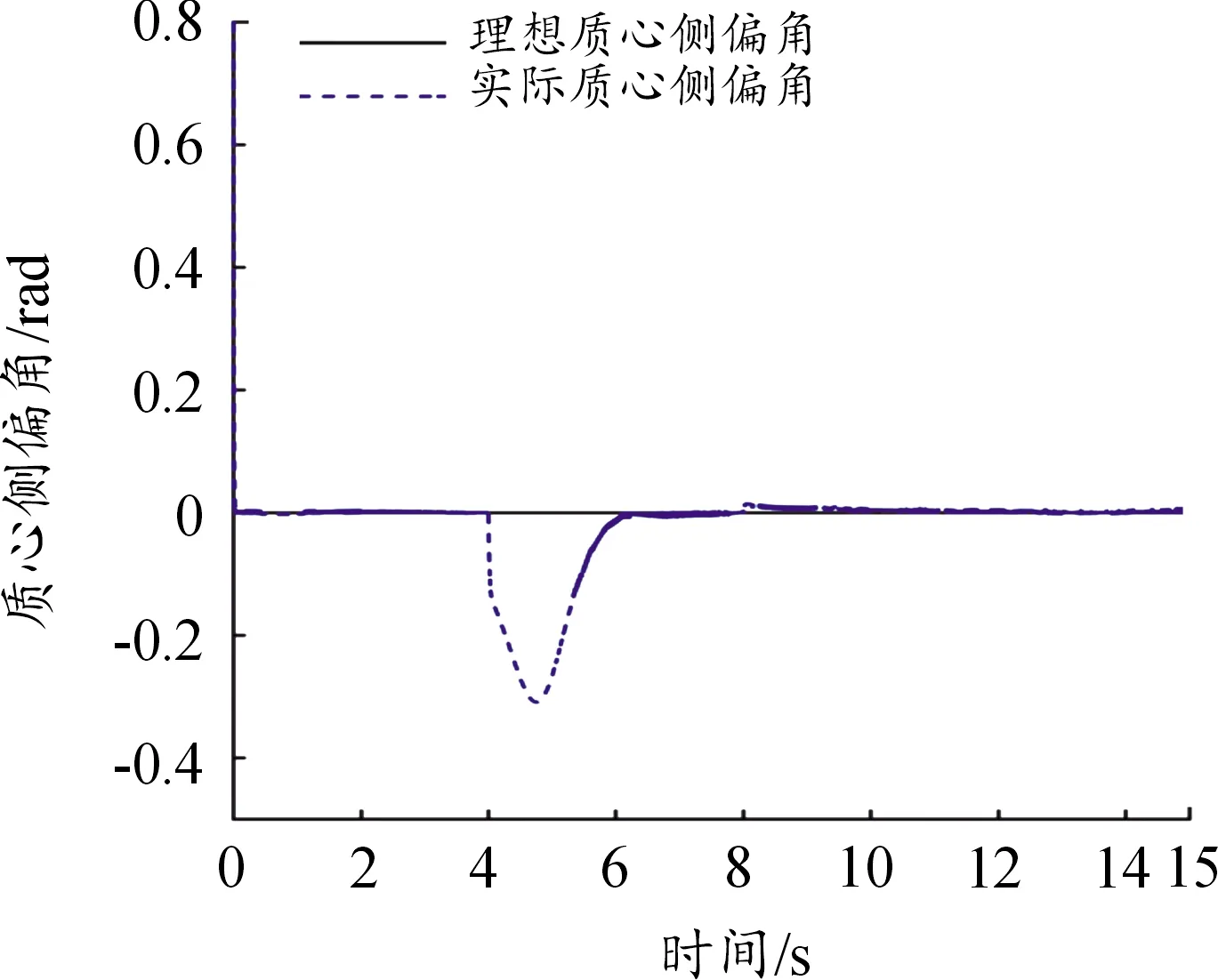
图3 质心侧偏角跟踪曲线
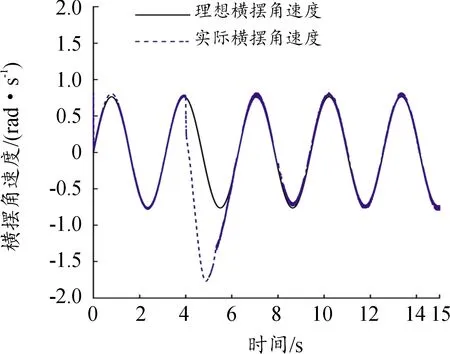
图4 横摆角速度跟踪曲线

图5 无控制质心侧偏角跟踪曲线
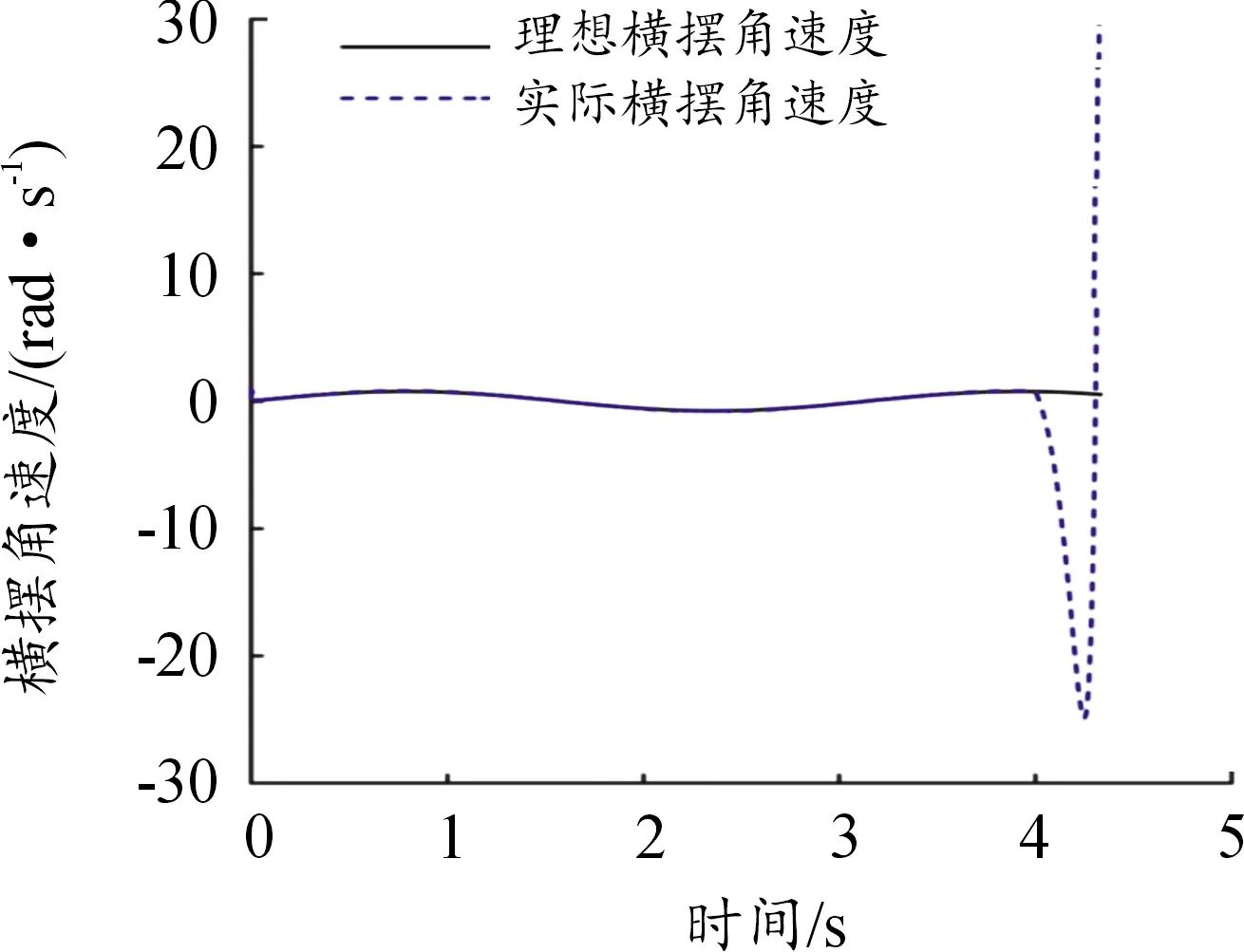
图6 无控制横摆角速度跟踪曲线
4 Carsim和Simulink联合仿真分析
通过前面的Simulink仿真验证,基于建立的简易2自由度模型基本证明了容错控制策略的有效性。为了更好地进行研究,需要在更加真实的模型上进行验证,但考虑执行机构故障情况下的实车试验具有极大的安全隐患,且高成本的改装也进一步限制了实车试验的进行。Carsim作为一款成熟的商业软件,自带的数据库经过大量的试验验证,参数准确可靠,可以替代实车进行各种工况下的仿真试验。因此,选择在Carsim模型中完成目标汽车模型的修改,并在Matlab/Simulink平台进行上层控制器的设计,实现联合仿真。
4.1 Carsim整车模型建立及验证
选取Carsim中的B级车,通过设置参数屏蔽机械转向系统[22],实现四轮转角信号由外部输入。设置整车输入接口为四轮转角,输出为质心侧偏角和横摆角速度。为了验证所建立的整车模型的正确性,选取4个车轮转角为相同的连续正弦输入信号搭建模型如图7所示,仿真时间为15 s,整车运动过程中3D模型如图8所示,仿真结果如图9所示。

图7 正弦工况系统模型

图8 整车3D模型
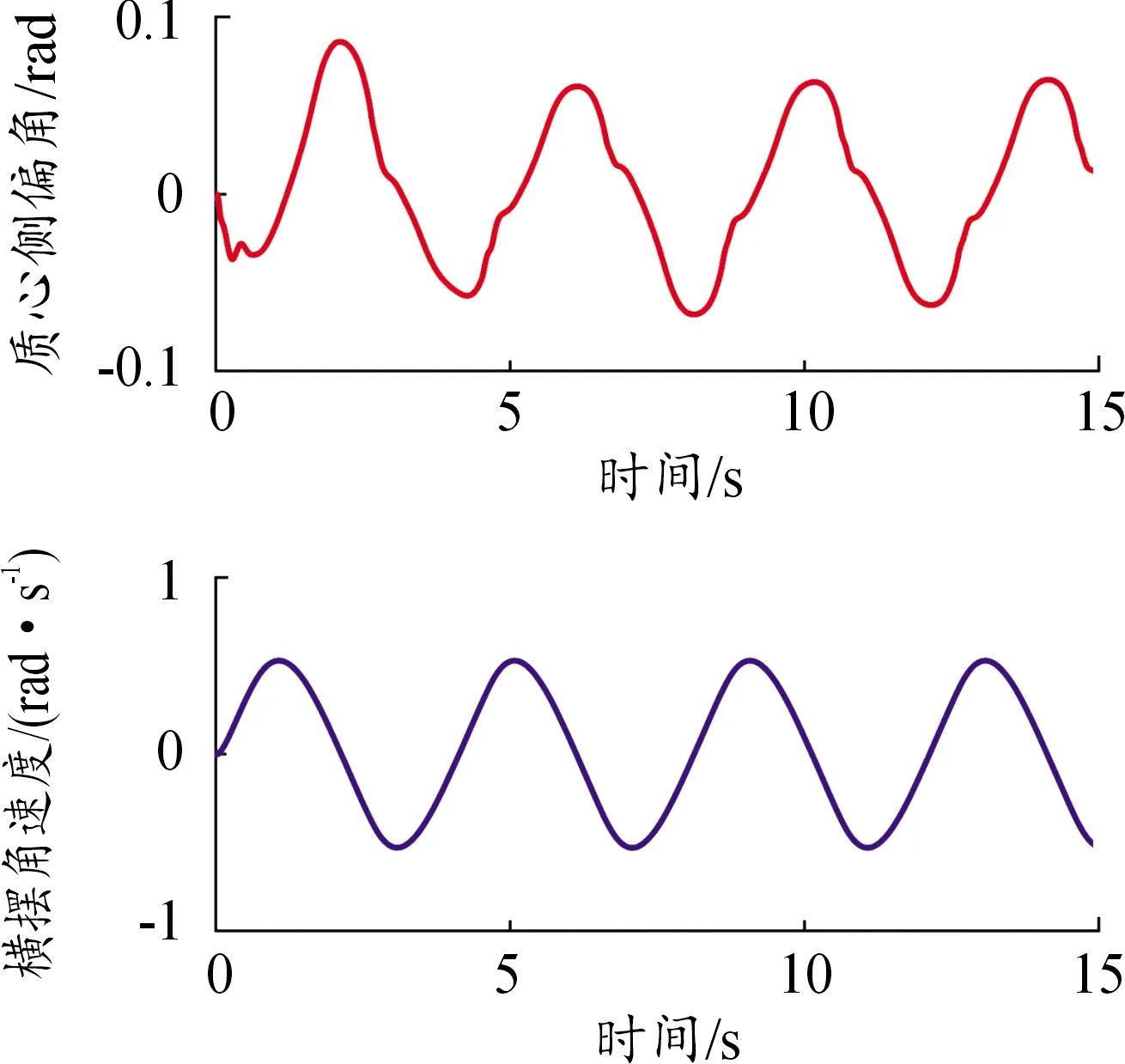
图9 状态量变化曲线
根据图9和输入的四轮转角信号,可知车子在正弦信号作用下做蛇行运动,但质心侧偏角的变化幅度较大,主要是因为4个车轮转角始终保持一致,整体运动过程由众多斜行运动组成,在车轮转角最大的时刻导致质心处的速度方向和车头方向形成较大的质心侧偏角。仿真结果充分表明了所建立的四轮独立转向整车模型的正确性。
4.2 仿真分析
为了验证所设计的容错控制器的有效性,建立联合仿真模型,如图10所示。
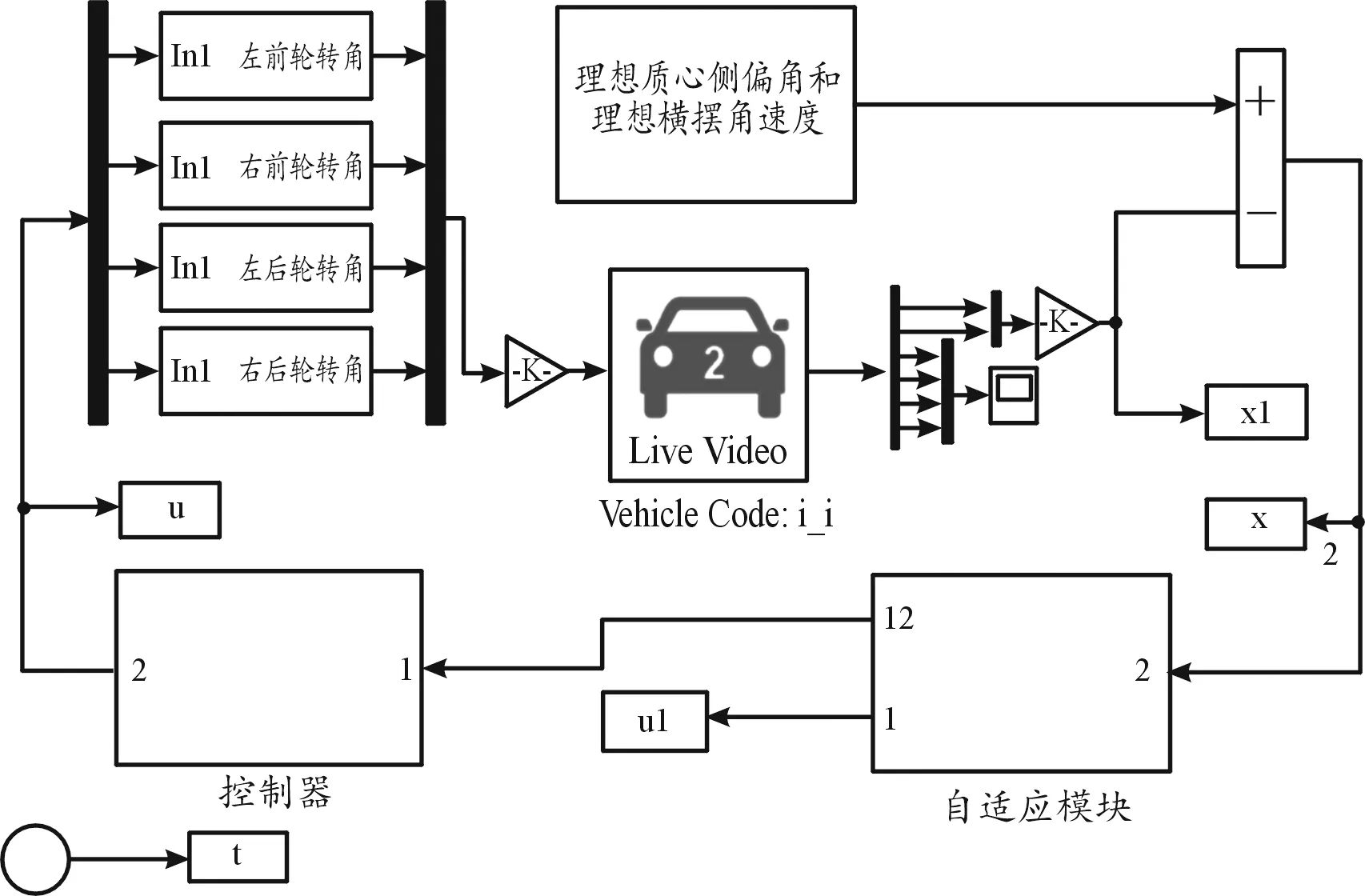
图10 联合仿真模型
图11、12表示的是在设置以上故障时的系统质心侧偏角和横摆角速度跟踪曲线。由图可知在t=5 s时,第1个执行器发生中断故障时,车辆的质心侧偏角和横摆角速度均发生较大波动,车辆处于失稳状态,经过控制器的持续调节,并在4 s时间内快速恢复到跟踪理想值,误差逐渐趋向于零;t=9 s时第1个执行器出现时变卡死故障,第2个执行器出现时变失效故障,在此种复杂工况下,质心侧偏角和横摆角速度依然能被控制在较小范围波动,使实际值和理想值之间的跟踪误差在小范围内波动。以上联合仿真结果证明:所设计的容错控制器能够有效提高系统的容错能力,保证系统的渐近稳定,提高车辆在转向过程中的安全性。
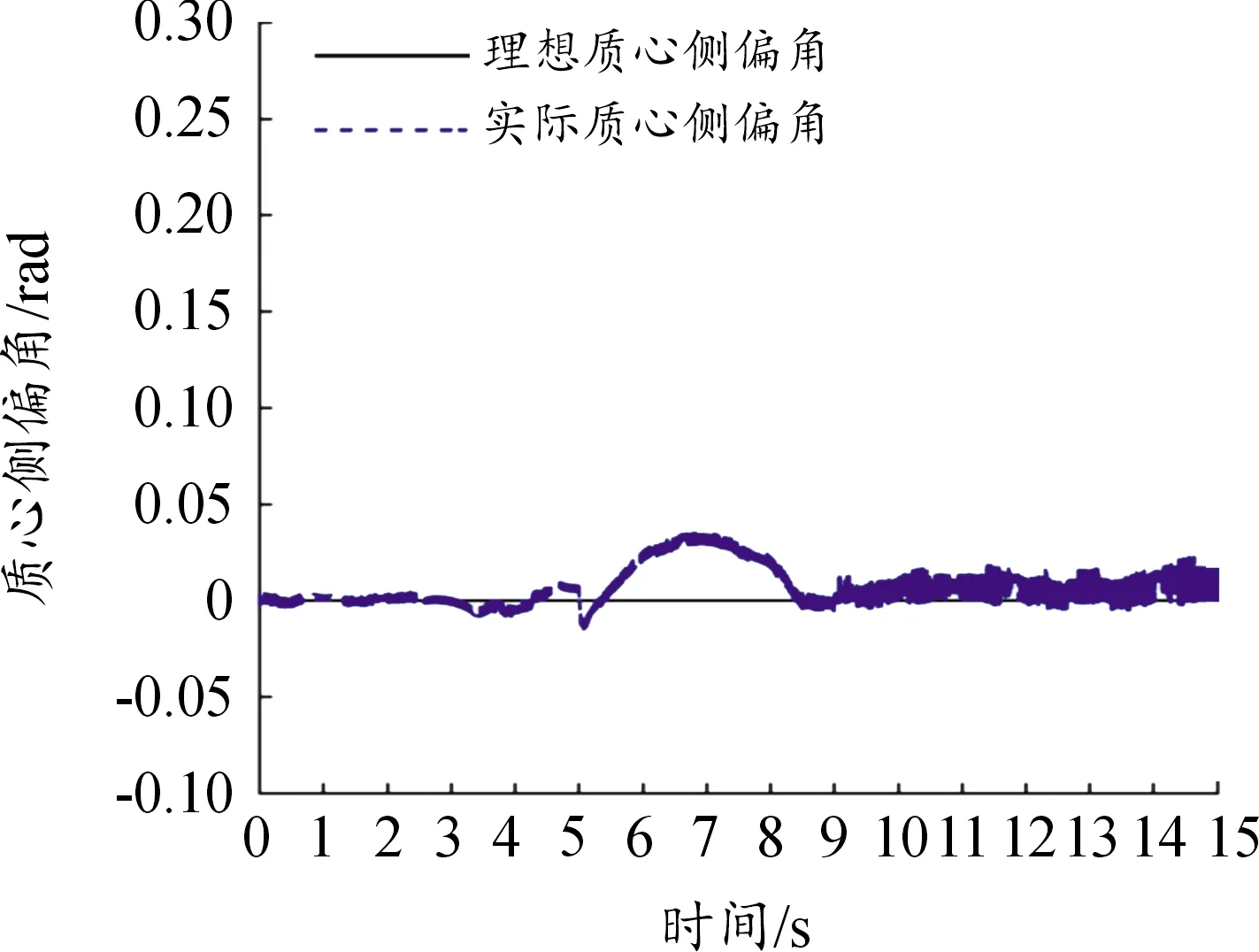
图11 质心侧偏角跟踪曲线
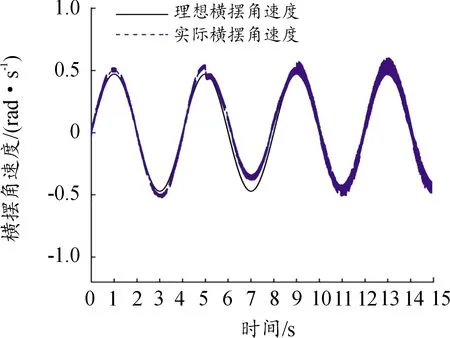
图12 横摆角速度跟踪曲线
5 结论
针对线控四轮转向汽车执行器故障的主动容错控制方法进行研究,将直接自适应容错控制方法应用到线控四轮独立转向系统。以跟踪理想质心侧偏角和横摆角速度为目标设计的上层容错控制器为提高线控转向系统执行机构的容错能力提供了一种可行的方法。Matlab仿真结果和Carsim/Simulink联合仿真结果均表明,所设计的容错控制器能够实现线控四轮独立转向汽车在执行器出现部分失效、中断和卡死故障时对理想模型的跟踪,能够有效提高系统的容错能力和可靠性。
