Phase-type分布下的信度模型
2021-11-06房婷婷
房婷婷,窦 燕
(新疆财经大学, 乌鲁木齐 830012)
信度理论是一种重要的经验估费方法,精算师利用过去n年的索赔数据预测第n+1年的最优保费,而研究信度保费最重要的环节是关于损失数据X=(X1,X2,…,Xn)的分布的讨论。
经验表明:由于历史数据的不稳定性很难给出索赔数据的分布,有学者提出采用在更一般的分布框架下建立信度模型,这样可以使估计结果具有更强的通用性和稳健性。例如, Hassan Zadeh等[1]研究了Phase-type分布下的贝叶斯保费和信度保费。其次,经典信度模型中使用的对称损失函数仅关注了估计值的精确度,忽略了拟合度的重要性。因此,许多学者致力于研究非对称损失函数下的信度保费。例如,温利民等[2-3]分别在指数损失函数及Linex损失函数下推导了信度保费;王娜娜[4]在熵损失函数下推导了信度保费;张强等[5]在加权平衡损失函数下推导了信度保费;房婷婷等[6]在Mlinex损失函数下推导了信度保费。此外,在经典信度模型中常假设索赔数据服从某个分布,实际上,历史索赔数据X1,X2,…,Xn分布通常是未知的。在此情况下,胡莹莹等[7-8]研究了最大熵方法下的信度估计及纯稳健信度估计。章溢等[9]讨论了概率密度函数的信度模型。李新鹏等[10]推导了具有风险相依效应的信度模型。
经典信度理论中,确定合适的Xij|θi的分布是十分困难的,这是因为个体经验数据不能用某个特定的分布描述。因此,采用具有多样性结构的分布将使预测结果更加精确。进一步地,在索赔数据分布未知情况下,需要讨论如何计算信度保费才更符合实际要求。而在建立信度模型时,使用非对称损失函数可以避免由对称损失函数引起的高保费征收问题,寻找合适的非对称损失函数尤为必要。结合以上问题,本文以具有多样性结构的Phase-type分布为基础,首先讨论了带通货膨胀因子的单合同信度保费和精确信度;再将信度估计结果推广到多合同情况;最后,推导了平衡损失函数下的多合同信度保费及精确信度形式;最后进行数值模拟部分,展示模型的稳健性。
1 Phase-type分布
Phase-type分布描述了具有有限个瞬时态和一个吸收态的马尔可夫过程进入吸收态的时间分布。Phase-type分布有许多优秀的性质,其一,它可以近似为任何一种分布;其二,用PH分布代替指数分布,使得其在算法上更易求出显式解。这些性质使得PH分布广泛应用于卫生保健、金融、运输等领域,但在保险精算方面的研究却少之又少。
考虑一个有n+1个状态的连续时间马氏链{X(t),t≥0},其中{1,2,…,n}为瞬时态, {n+1}为吸收态。另外,假设n+1个状态的初始概率为(π,πn+1),这里πn+1=1-π′1,1是元素为1的列向量。记无穷小生成元Q为
这里D0为n×n的矩阵,d1为n×1的列向量。由于Q为马氏链的生成元,所以有
Dij≥0, for 1≤i≠j≤n
Dii<0, for 1≤i≤n
和
D01+d1=0
定义1[1]若马氏链进入吸收态{n+1}的时间分布为
X(t)=inf{t≥0,X(t)=n+1}
则称X(t)为PH分布,记作X~PH(π,D0)。
根据定义,随机变量X的概率密度函数有以下形式:
引理1[1]若X~PH(π,D0),则X的概率密度函数为
f(x)=π′exp(D0x)d1,x≥0

不失一般性地,D0可以写成
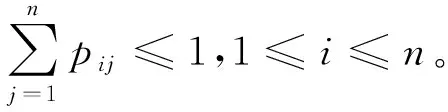

P=I+(1/θ)D0
这里矩阵I为n阶单位阵。因此,P可以写作
(1)
且
引理2[1]X|θ~PH(π,D0)的密度函数可以写成无穷个Erlang分布密度函数的和:

qn+1=π′Pn(I-P)1≥0,n=0,1,…
(2)
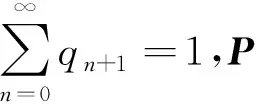
2 带通货膨胀因子的信度保费及精确信度
在经典信度理论中,给定风险参数Θ=θ时,索赔X1,X2,…,Xn是独立同分布的,并且E(Xi|Θ)=μ(Θ),Var(Xi|Θ)=υ(Θ)。然而,每年的索赔数据会受到通货膨胀因子的影响。因此,需要建立带通货膨胀因子的信度模型。假设某保单n年的索赔数据为X=(X1,X2,…,Xn),这些索赔数据的风险参数为Θ,Θ的先验分布为π(θ)。本节的目的是预测第n+1年的索赔。首先假设给定Θ=θ时,X1,X2,…,Xn条件独立同分布,且
E(Xj|Θ)=rjμ(Θ)
Var(Xj|Θ)=r2jσ2(Θ)
j=1,2,…,n
(3)
其中r为每年的通货膨胀因子,并记
(4)
定理1在假设条件(3)(4)下,Xn+1的最优线性信度估计为
(5)
证明:
为得到Xn+1的最优线性信度估计,首先最小化下式
(6)
对(6)关于α0和αj求偏导并令结果为0,有
基于式(3)(4),可得
(7)
(8)
联立式(7)(8),有
因此,可得
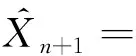
综上,定理1得证。
根据式(5),假设随机变量Xi|Θ服从PH分布,则它可以写成N个参数为Θ的指数分布的和,即
Xn+1=Y1+…+YN
(9)
这里Yj,j=1,2,…,N是相互独立的指数分布。N表示马氏链到达吸收态的转移数且N~PHd(π,P),P如式(1)所示。则Xn+1的条件均值和条件方差可以写成
rn+1μ(Θ)=E(Xn+1|Θ)=E(Y1|Θ)E(N)=
Θ-1E(N)
r2(n+1)υ(Θ)=Var(Xn+1|Θ)=
Θ-2(Var(N)+E(N))

(10)
因为N~PHd(π,P),易计算出式(10)的前半部分。特别地,若风险参数Θ~Γ(Κ,γ),即
那么式(10)的后部分可以写成
综上,信度保费(5)可表示为
接下来讨论带通货膨胀因子的精确信度。
Jewell[11]证明了在均方损失函数下,若给定Θ=θ时,损失X1,X2,…,Xn服从参数为θ的指数分布,且Θ的先验分布π(θ)服从指数分布族,则贝叶斯保费具有信度保费的形式。对于带通货膨胀因子的信度模型,得到的结论如下。
定理2在假设条件(3)(4)下,给定Θ=θ时,若条件密度函数fXj|Θ(xj|θ)有线性指数分布族的形式:
且共轭先验分布为
(11)
其中π(θ0)=π(θ1)=0,那么精确信度存在。
证明:
因为E(μ(Θ))=μ且
下面有

(q(θ))-k*e-θμ*k*
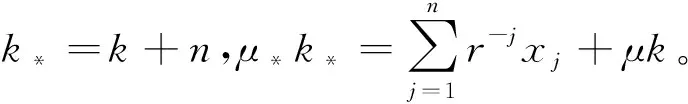
即叶斯保费E(Xn+1|X)具有信度保费的形式,精确信度存在。
下面讨论PH分布下的精确信度形式。由式(9),有
Xi=Yi1+…+Yi,Ni,i=1,…,n+1
假设X1,X2,…,Xn+1相应的嵌入式马尔可夫链为U1,U2,…,Un+1,参数记为(π,D0)。给定Θ=θ时,变量U1,U2,…,Un+1是条件独立的。另外假定:
1) 给定Θ=θ和i时,Yij,j=1,…,Ni为条件独立同指数分布的随机变量。
2)Ni,i=1,…,n+1为独立同分布的随机变量,且与Θ独立。
3)Θ服从如式(11)所示的先验分布。
因此,给定Θ=θ时,损失X1,X2,…,Xn+1独立同分布且服从参数为(π,D0)的PH分布。那么
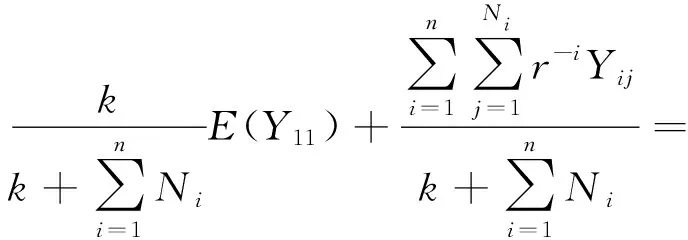
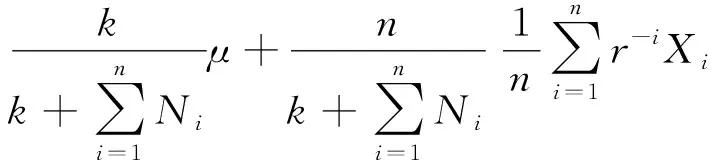
(12)
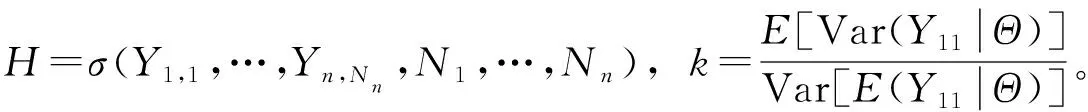
因为σ(X1,X2,…,Xn)是H的子集,在(12)两边取关于X1,X2,…,Xn的条件期望后会有
E(Yn+1,1|X1,X2,…,Xn)=
又因为
因此,

(13)
此时, 贝叶斯保费可以写成如下形式
以上结果可以推广到多合同情形。类似地,假设给定Θi=θi时,Xi1,…,Xin,i=1,…,m独立同分布,且有E(Xij|Θi)=rjμ(Θi),Var(Xij|Θi)=r2jυ(Θi)。另外,记μ=E(μ(Θi)),υ=E(υ(Θi)),a=Var(μ(Θi))。由此易得带有通货膨胀因子的多合同模型下的信度保费及精确信度,下文不再赘述。
3 平衡损失函数下的信度保费及精确信度
假设某保险公司有m份保单,第i份保单的索赔数据记作Xi=(Xi1,Xi2,…,Xin)′,i=1,…,m。每份保单的风险参数记为Θi,先验分布为π(θ)。本节的目标是预测下一年的保费,即μn+1(Θi)=E(Xi,n+1|Θi)。下面给出一些假设条件和记号:
假设1给定Θi=θi时,Xi1,Xi2,…,Xin,i=1,2,…,m条件独立同分布,并有
E(Xij|Θi)=μ(Θi),Var(Xij|Θi)=σ2(Θi)
假设2{(Xi,Θi),i=1,2,…,m}相互独立,Θ1,…,Θm独立同分布。并记
E(δ0i)=E(μ(Θi))=μ, Cov(δ0i,Xij)=si
Var(μ(Θi))=τ2,E(σ2(Θi))=σ2
其中δ0i(x)为第i份保单的目标保费。
由Zellner[12]定义的平衡损失函数
(14)
可以得出如下结论。
定理3根据假设条件1、2及平衡损失函数(14),μ(Θi)的最优线性非齐次估计为
证明:
由假设1、2易知,E(Xij)=μ,Var(Xij)=τ2+σ2,且
Cov(Xij,Xij′)=τ2,Cov(Xij,Xi′j′)=0,i≠i′,j≠j′
Cov(μ(Θi),Xij)=τ2,Cov(μ(Θi),Xi′j)=0,i≠i′
令
(15)
对式(15)关于α0求偏导并令结果为0,有
将α0代入Φ,那么
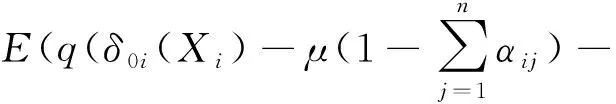
(16)
对式(16)关于αij′求偏导并令结果为0,则有
因此可得
则在平衡损失函数下,μ(Θi)的最优线性非齐次估计为
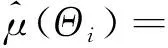
综上,定理3得证。
假定Xij|Θi~PH(π,D0),那么Xij可以写成:
Xij=Yij1+Yij2+…+YijN
(17)
这里给定Θi=θi时,Yijl,l=1,2,…,N独立同分布且服从参数为θi的指数分布。N表示马氏链到达吸收态的转移数,N~PHd(π,P)。
定理4假设给定Θi=θi时,随机变量Xi1|Θi,…,Xin|Θi独立同分布且服从PH(π,D0)。 若Θi服从如下分布
(18)
则基于平衡损失函数式(14)得到信度保费估计为
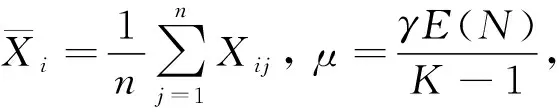
证明:
Xij|Θi的条件均值和方差可以表示为
μ(Θi)=E(Xij|Θi)=
σ2(Θi)=Var(Xij|Θi)=
E2(Yij1|Θi)Var(N)+
E(N)Var(Yij1|Θi)=
所以有
又因为N~PHd(π,P),则
E(N)=π′(I-P)-11
E(N(N-1))=2π′P(I-P)-21
那么,
Var(N)+E(N)=E(N2)-E2(N)+E(N)=
E(N(N-1))+2E(N)-E2(N)=
2π′P(I-P)-21+2π′(I-P)-11-
(π′(I-P)-11)2=2π′(I-P)-21-
(π′(I-P)-11)2
另一方面,Θi服从式(18)所示分布,显然有


综上定理4得证。
温利民等[13]得出了在平衡损失函数下精确信度存在的结论,即

由式(17),这里有
Xi,n+1=Yi,n+1,1+Yi,n+1,2+…+Yi,n+1,Nn+1
假设Xi1,Xi2,…,Xin+1相应的嵌入式马尔可夫链为Ji1,Ji2,…,Jin+1,参数是(π,D0)。给定Θi=θi,变量Ji1,Ji2,…,Jin+1是条件独立的。此外,本文还假设:
1) 给定i,j及Θi=θi时,Yijk,k=1,2,…,Nj为条件独立同分布且服从指数分布。
2)Nj,j=1,…,n+1为独立同分布随机变量,并独立于Θi。
3)Θi,i=1,…,k服从(18)的先验分布。
基于以上假设条件,有
E(Yi,n+1,1|H)=
(19)
这里H=σ(Y1,1,1,…,YK,n,Nn,N1,…,Nn)。考虑在式(19)两边求关于Xi1,Xi2,…,Xin的条件期望。那么
E(Yi,n+1,1|Xi1,Xi2,…,Xin)=
进一步地,
E(Nn+1)E(Yi,n+1,1|H)
因此, 贝叶斯保费可以写成
4 数值模拟

因为
E(N)=π′(I-P)-11
Var(N)+E(N)=2π′(I-P)-21-
(π′(I-P)-11)2
则
E(N)=2.06,Var(N)+E(N)=4.93
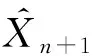

图1 信度保费的MSE曲线
由图1可以看出MSE随着θ的增加而减小,如:
θ=187.78时,MSE=0.000 38
θ=241.58时,MSE=0.000 31
预测结果具有较高精度。
例2 取式(11)中Gamma先验分布的参数为γ=1,K=2,通货膨胀因子r=1.02。矩阵P为

令MSE1,MSE2分别表示定理1的信度保以及经典信度保费的均方误差,分别取n=5、10、15完成5 000次模拟,所得结果如表1所示。

表1 定理1的信度保以及经典信度保费的均方误差
由表1可知:PH分布下的信度保费的精确度远高于经典信度保费,这是因为PH分布具有多样性结构,提高了索赔数据分布的拟合度。
5 结论
1) 由于服从PH分布的随机变量的构成特点,单合同的索赔数据是稳定的并易于预测。
2) 考虑通货膨胀因素的信度模型,预测的保费更符合实际情况。
3) 带有非对称损失函数的信度模型拟合优度高,估计结果更准确。
在带有通胀因子和非对称损失函数的信度模型的背景下,假设索赔数据对风险是独立的。然而在大多数情况下,索赔之间具有很强的依赖关系[14-15]。因此,在今后的工作中,可以针对索赔数据的相依性进行研究。
