车用螺旋型水道永磁同步电机温升特性

何联格，石文军，陈红玲，张 斌，聂远航，吴欣阳

(1.重庆理工大学 车辆工程学院，重庆 400054；2.重庆理工大学 汽车零部件先进制造技术教育部重点试验室，重庆 400054；3.重庆青山工业有限责任公司，重庆 402761)

由于永磁电机具有高转速、高功率密度、结构简单及工作效率高等优点，在各领域应用非常广泛[1-2]。由于车用永磁同步电机功率密度大，工作环境封闭，散热困难，导致电机温度过高，从而引起永磁体不可逆退磁和绕组绝缘层快速老化失效等问题，因此研究永磁同步电机的冷却系统对电机运行可靠性具有重要意义[3-4]。

电机的冷却方式主要有自然冷却、风冷、水冷、油冷以及混合冷却等。赵兰萍等[5]对比研究了自然风冷和油冷2种冷却方式对轮毂电机温升特性的影响。吴琳等[6]对比研究了电机在风冷和水冷下的温升特性，得出水冷具有良好的冷却效果。水冷系统具有成本低、效果好的优点，使用较广泛。现有对水冷电机的研究，集中在散热结构设计和优化[7-9]。刘慧娟等[10]利用3D有限元法对比分析了永磁同步电机在不同水道结构、不同注水方式、不同冷却液温度和流量下的温度场分布。李晓艺等[11]提出一种轴向Z字形互逆双水道模型，分析得出互逆双水道能在一定程度上改善电机的冷却效果。Zhang等[12]研究了车用永磁同步电机水道的长度、宽度、水道层数以及电机机壳厚度对电机冷却效果的影响。综上可知，已有文献在冷却系统的研究中，主要分析了单水道模型下的温升特性。

本文以某38 kW车用永磁同步电机样机为研究对象，利用Maxwell和CFX仿真软件对样机电磁场与温度场进行仿真分析。通过与试验结果进行对比分析，验证了仿真计算方法和模型的准确性。在此基础上，提出一种对流双水道电机模型，并对其进行温度场仿真计算，将计算结果与单水道电机模型进行对比分析，得出对流双水道电机模型具有更好的冷却效果的结论。

1 电机原模型下的温度场仿真

1.1 电机基本参数

本文以一台48槽/8极永磁电机为基础，对该电机在38 kW、4 000 r/min工况下的温升特性进行分析，基本参数见表1。

表1 样机基本参数

1.2 电机热源计算

该样机损耗主要是由绕组铜耗、定转子铁芯损耗、永磁体涡流损耗、风磨损耗组成。其中铜耗和风磨损耗采用公式计算，定转子铁芯损耗和永磁体涡流损耗通过仿真计算得到。

绕组铜耗主要来自于铜线内阻，为了简化计算过程在计算铜耗时不考虑温度对电阻的影响，谐波以及集肤效应，直接采用式(1)计算

PCu=mI2R

(1)

式中：PCu为绕组铜耗；m为电机相数；I为相电流；R为绕组内阻。

风磨损耗是转子旋转过程中，转子表面与空气发生摩擦而产生。采用式(2)计算

(2)

式中：PF为风磨损耗；n1为转子的转速；Dr为转子外径；lr为转子轴向长度。

在永磁体和三相交流电的相互作用下，定、转子内部形成复杂多变的磁场[13]。为了快速准确地得到包括磁滞损耗、涡流损耗和异常损耗的定转子铁芯损耗，以及全面考虑定子开槽和定子绕组分布引起空间谐波以及定子电流的非正弦引起的时间谐波[7]引起的永磁体涡流损耗，直接利用Maxwell进行瞬态电磁仿真，得到电机各部件具体损耗值，如表2所示。

表2 热源分布

1.3 仿真模型的建立

1.3.1温度场分析的几点假设

永磁同步电机的热源比较多，热量的传递过程十分复杂。为了简化仿真过程，提出如下几点假设[14]：

① 电机绕组、定子铁芯、转子铁芯、永磁体和气隙各部分产生的热量分别均匀分布。

② 忽略各个部件之间的装配间隙。

③ 忽略电机在温升过程中的热辐射。

④ 忽略温度对电机各个部件的导热系数以及表面对流换热系数的影响。

⑤ 电机内部冷却气体流速远小于声速，即马赫数很小，故冷却水为不可压缩流体。

1.3.2热传导数学模型

根据热传导理论，在笛卡儿坐标系内，求解域内热传导微分方程为

(3)

式中：λx、λy、λz为电机内各介质在x、y、z方向的热导率；T为物体的温度；qv为热源密度；ρ为物体的密度；c为物体的质量热容；Tw为边界温度值；τ为时间项；S1、S2、S3为物体边界；Tf为流体温度；α为流体与壁面间的表面对流换热系数。

1.3.3温度仿真模型

经过对模型网格质量仿真分析时长等综合考虑，对电机进行一系列简化，建立包括机壳、水道、冷却水、定子、绕组、转子、永磁体和轴的仿真物理模型，如图1(a)所示。为了方便仿真前处理，遵循绕组总体体积不变的原则，将多匝绕组等效为实心一体模型，如图1(b)所示。

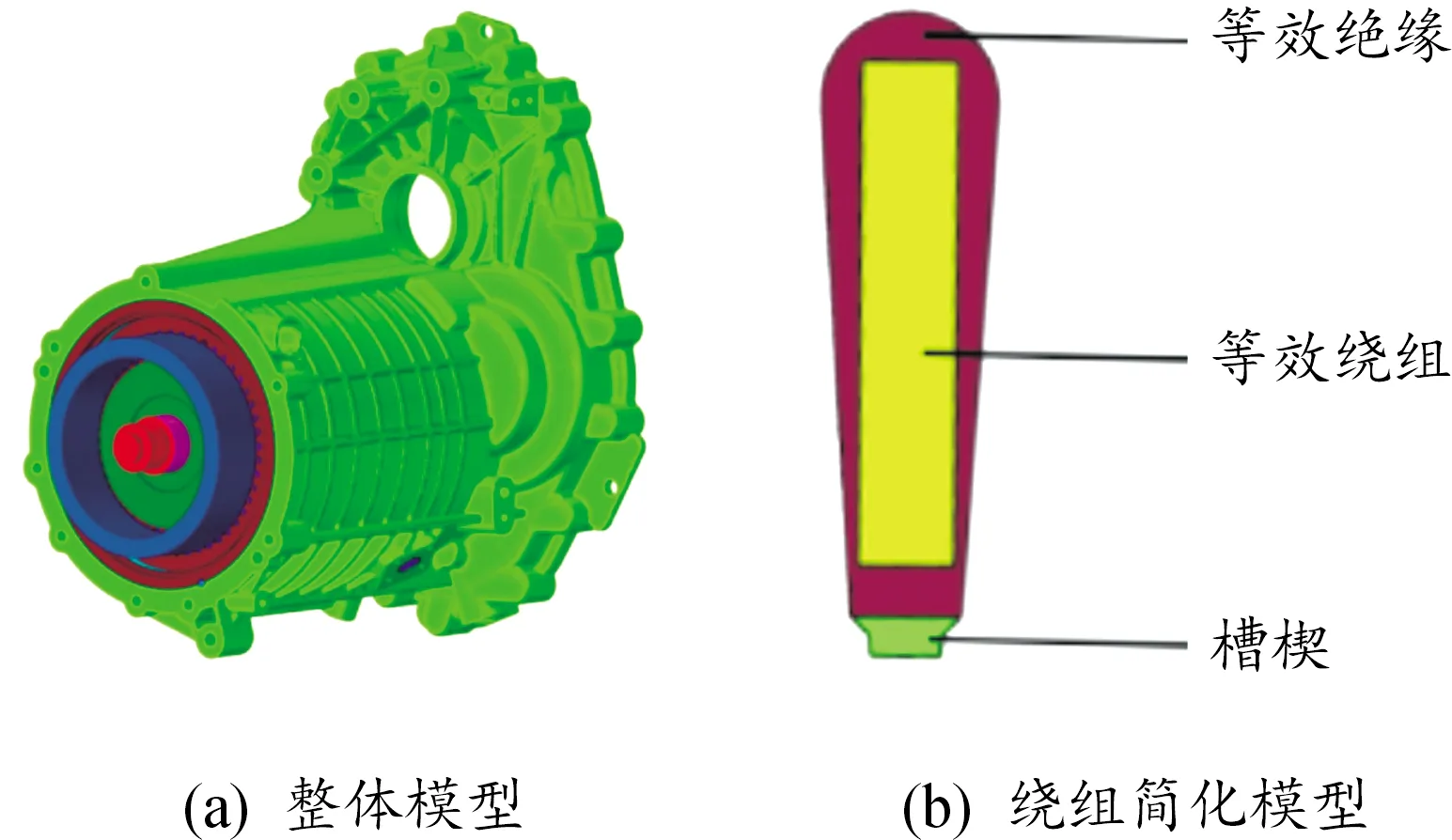
图1 电机温度场简化模型

1.4 导热系数的确定

1.4.1绝缘层等效导热系数

由于在定子槽内有不均匀分布的槽内浸漆层、槽绝缘层、绕组绝缘层以及槽内间隙，为了方便建模和计算，将所有绝缘材料等效为一体，如图2(c)所示。等效绝缘层的导热系数可根据式(4)计算[15]

图2 各位置温度分布云图

(4)

式中：λ0为绝缘体等效导热系数；δi为(i=1、2、3、4)各种绝缘体的等效厚度；λi为(i=1、2、3、4)各种绝缘体的等效导热吸收。

1.4.2气隙的等效导热系数

虽然定、转子气隙厚度很薄，但是对电机温升过程的影响很大。为了方便仿真前处理，将转子和气隙假设为静止，气隙为固体，将原来的热对流变为热传导。根据文献[16]引入气隙的等效导热系数λa，根据气隙的流动状态对其等效导热的计算如下：

(5)

式中：Reg为等效气隙雷诺数；Dr为转子外径；n1为转子转速；γa为空气动力粘度；g为气隙厚度；Recr为等效气隙临界雷诺数；Ds为定子铁芯内径。

若Reg小于Recr，定、转子间空气流动状态为层流，气隙等效导热系数为空气导热系数；若Reg大于Recr，定、转子间空气流动状态为湍流，此时气隙等效导热系数λa可根据以下公式计算：

(6)

式中：λa为气隙等效导热系数。

1.5 温度场仿真分析

1.5.1边界条件设置

该电机的温度场仿真边界条件设置如下:

① 将电机环境温度设置为65 ℃。

② 冷却水入口设置为速度入口，流速为8 L/min，温度为30 ℃。

③ 冷却液出口设置为零压力出口。

④ 仿真计算中所有流固耦合面兼为无滑移边界。

⑤ 电机内各零件的端面散热系数参考文献[14]进行处理。

1.5.2温度场求解

通过对电机在38 kW、4 000 r/min工况下的瞬态温度场仿真计算，各位置温度分布情况如图2所示。最高温度出现在绕组端部，为87.5 ℃；永磁体最高温度为63.7 ℃;定子最高温度也出现在端部，为64.4 ℃。电机各部件都出现两端温度高于中间温度的现象，绕组和定子的温差较大，其他部件相对较少，主要是因为绕组两端端部热量大且无法直接通过冷却水冷却。

2 电机温升试验与仿真对比

对样机进行台架试验，如图3所示。试验采用热电偶法，因为绕组端部温度最高，所以试验主要监测绕组端部温升状况。虽然热电偶直接接触被测绕组，为了避免绕组周向温差导致试验结果不够准确，在绕组温度较高端均匀地放置4组热电偶。

图3 电机温升台架试验测试

将所读取的4组数据的均值作为最终试验数据，与仿真温度值对比，如图4所示。样机在前300 s温度上升较快，试验数据中300～1 200 s的温度虽然有微小波动，但是整体上呈缓慢上升，到1 200 s温度基本达到稳定，仿真温度稳定在87.5 ℃，试验温度为90 ℃，误差在允许范围内，并且仿真温度与试验温度变化趋势一致。验证了对电机温升过程的仿真计算方法和模型的准确性。

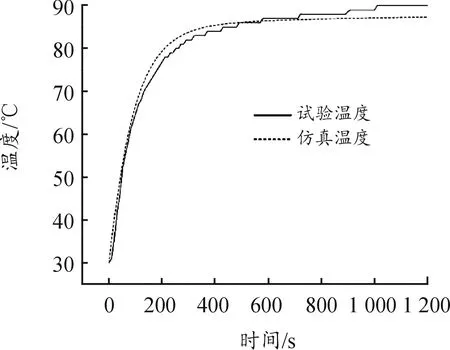
图4 仿真温度与试验温度曲线

3 对流双水道的提出和分析

3.1 对流双水道电机与单水道电机模型对比

为了研究对流双水道对电机温度场的影响，对该样机模型进行进一步简化处理。简化模型如图5所示，控制2种水道截面积相等。单水道入水口水流速度为8 L/min，温度为30 ℃，对流双水道有2个入水口，进水口流速各为4 L/min，温度为30 ℃。

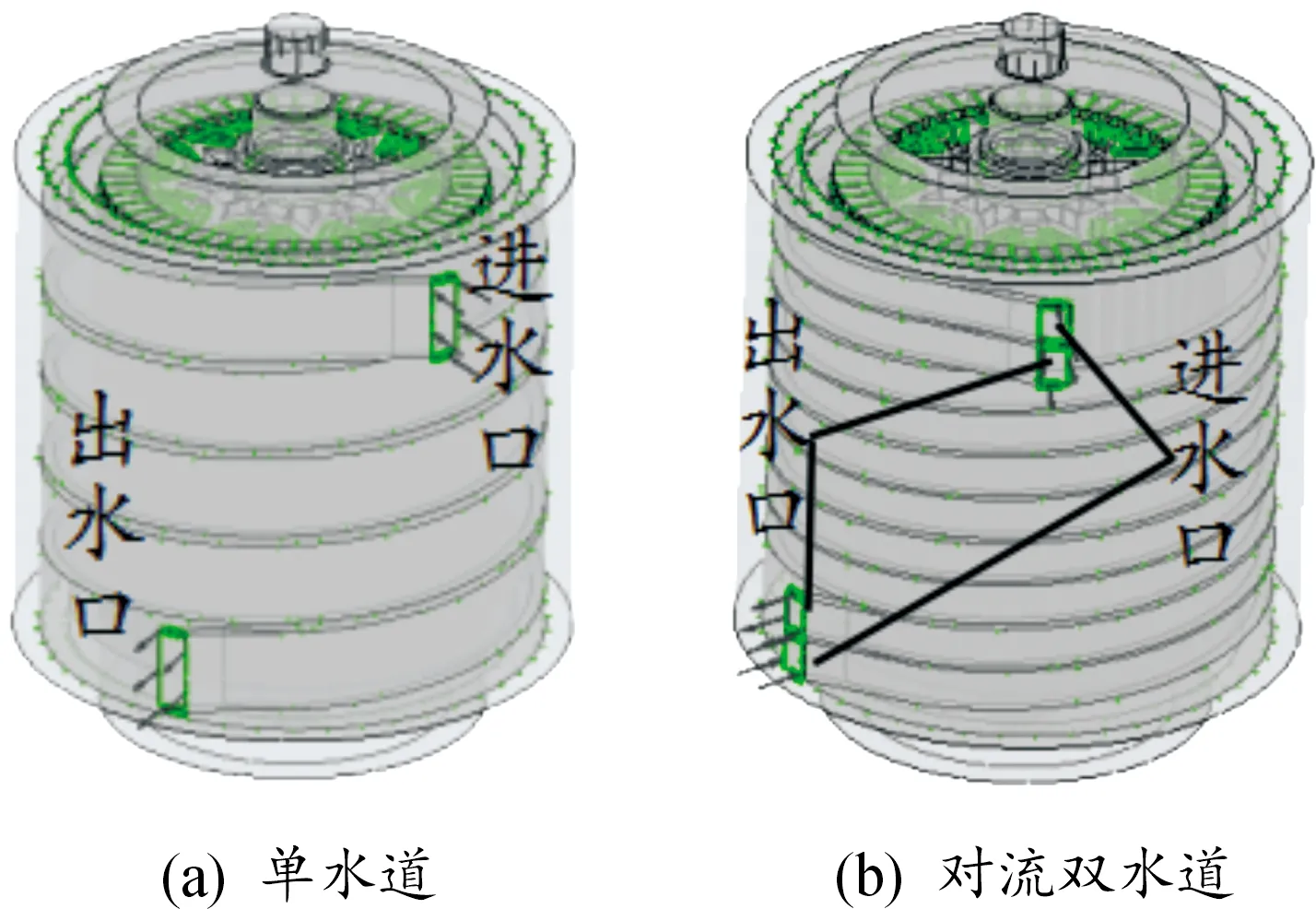
图5 2种水道下的电机模型

3.2 对流双水道模型电机与单水道模型电机温度场对比分析

3.2.1在38 kW、4 000 r/min下稳态温度场分析

以38 kW、4 000 r/min为例，模拟电动车在某低速工况下匀速运行。对2种水道结构下的电机进行CFX稳态仿真。

图6(a)显示单水道模型电机冷却水压降为 6 684 Pa，对流双水道模型电机冷却水压降为7 351 Pa，单水道模型电机比对流双水道模型电机压力损失大667 Pa。图6(b)分别是单水道模型电机水流速度与对流双水道模型电机水流速度，水流速度最高分别为1.19 m/s和1.24 m/s，对流双水道模型高于单水道模型0.05 m/s。通过对比2种水道模型的电机冷却水压降和流速可知，在水道横截面相同的情况下，对流双水道模型电机比单水道模型电机冷却水能量损失高10%。

图6 单双水道云图

对流双水道模型电机与单水道模型电机绕组轴向温度如图7所示。对比对高温度，双水道模型电机为88.3 ℃，单水道模型电机高于前者4.9 ℃，为93.2 ℃；对比平均温度，双水道模型电机为69 ℃，单水道模型电机为69.2 ℃，二者几乎相等；对比两端温差，双水道模型电机比单水道模型电机低11.1 ℃，为6.1 ℃；2种模型在轴向上的温差十分明显，双水道模型电机最大为35.3 ℃，单水道模型电机最大为41.2 ℃。

图7 2种水道模型下绕组轴向温度曲线

对流双水道模型电机与单水道模型电机转子轴向温度如图8所示。对比对高温度，双水道模型电机为61.5 ℃，单水道模型电机为63.1 ℃，前者比后者低1.6 ℃；对比平均温度，对流双水道模型电机略低，分别为59.4 ℃和59.6 ℃；对比两端温差和轴向最大温差，双水道模型电机都略低于单水道模型电机。

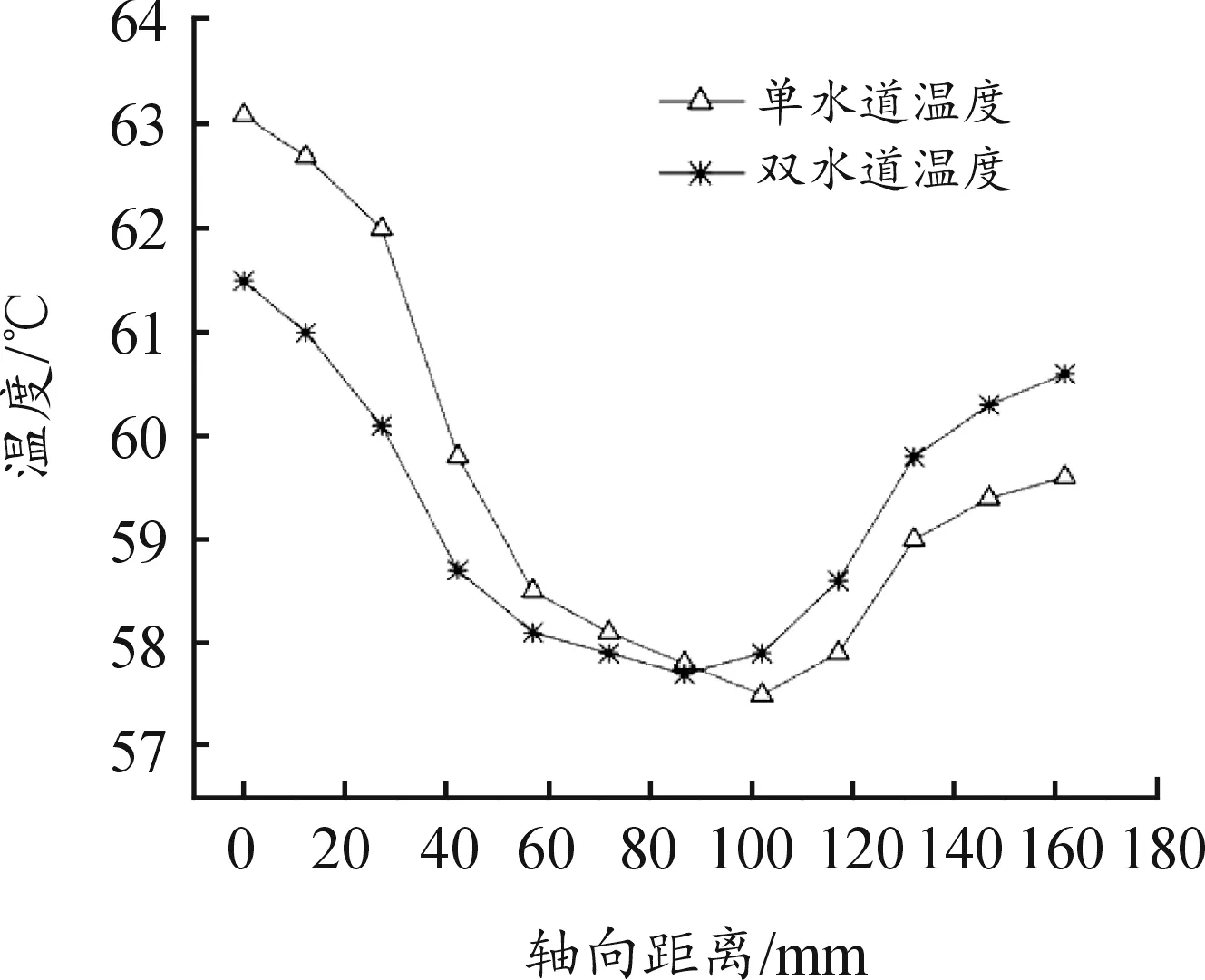
图8 2种水道模型下转子轴向温度曲线

对比对流双水道模型电机和单水道模型电机，虽然在绕组和转子在轴向平均温度上没有明显差距，但是对于电机在2种冷却水道下的最高温度，特别是绕组最高温度，双水道模型电机比单水道模型电机低5.3%，并且从绕组和转子的轴向温度对比可以看出，双水道模型电机温度在轴向上分布更加均匀。

3.2.2在74 kW、10 000 r/min下瞬态温度场分析

电机在74 kW、10 000 r/min下工作时，模拟汽车在短暂超车工况下的情景。对双水道对流模型电机和单水道模型电机进行瞬态温度场仿真，假设电机最大耐高温150 ℃。2种模型下的分析结果如图9所示。双水道模型电机达到150 ℃的时间在第65 s，单水道模型电机达到150 ℃的时间在第61 s，前者比后者晚4 s达到最高温度。在实际行车过程中，若采用对流双水道电机，在短暂的超车工况下行驶时，对比单水道电机可以多行驶4 s，若在该转速下电动车车速为100 km/h，采用对流双水道电机比单水道电机多行驶111 m，可以在一定程度上提高超车安全距离。

图9 2种水道模型下绕组达到150 ℃时间曲线

4 结论

1) 采用电磁场-流体场-温度场多物理场耦合的方法，仿真分析了样机在额定工况下持续运行时的温度场分布，并将计算结果与样机台架试验数据进行对比分析，验证了仿真计算方法和模型的准确性。

2) 通过对2种不同水道的电机模型的温度场对比分析可得，电机各个部件的温度轴向分布不均匀，尤其在绕组上表现最为明显，单水道和双水道模型的电机轴向最大温差分别达到41.2 ℃和35.3 ℃。

3) 对比分析2种不同水道的电机模型温度场计算结果可得，对流双水道电机模型不仅可以降低电机最高温度，而且使电机轴向温度分布更加均匀。

4) 通过对2种电机模型进行瞬态仿真结果对比分析，在74 kW、10 000 r/min条件下运行时，对流双水道电机模型比单水道电机模型达到150 ℃所用时间更长，表明双水道电机模型能在高功率高转速工况下运行更长时间。