齿轮故障振动信号精确幅值解调方法

李远政，丁 康，蒋 飞

(华南理工大学 机械与汽车工程学院，广州 510641)

齿轮在制造和安装过程中容易存在加工误差和轴不对中，导致实际振动响应信号产生幅值调制现象。此外，齿轮作为汽车变速器、风力发电机组以及航空航天等重大装备中的关键传动部件，长期处于高速重载等恶劣的工作环境中，极易出现齿轮磨损、齿形误差、齿轮轴弯曲等平稳型故障，同样使振动信号中出现幅值调制成分[1-2]，进一步增加了齿轮故障诊断的难度。因此，为了提高齿轮故障诊断的精度，急需一种齿轮振动信号的精确幅值解调方法。

常用的幅值解调方法主要有希尔伯特包络解调、广义检波滤波解调方法[3](平方解调、检波滤波解调和高通绝对值解调)、能量算子解调等。Ming等[4]迭代使用希尔伯特变换求包络并减去信号的直流偏置，可以从轴承故障的多分量信号中消除确定性谐波分量，保留循环脉冲响应的故障特征；Feng等[5]分别推导了行星轮轴承在内圈、外圈、滚动体故障时的显式调幅信号模型，并根据调幅信号包络谱中出现的特征频率成分进行轴承故障诊断；Feng等[6]基于本征时间尺度分解，提出了一种联合幅频解调分析方法，将行星轮系的故障振动信号分解为多个单分量信号，并借助包络解调谱和频率解调谱进行太阳轮、行星轮和内齿圈的故障诊断；Cheng等[7]利用经验模态分解(EMD)把多分量的调幅调频信号分解为多个固有模态函数(IMF)，并对每个IMF进行能量算子解调得到包络谱，用于滚动轴承故障诊断。徐元博等[8]提出了对称差分解析能量算子，能从重度污染的信号中解调出微弱故障信号频率。张文义等[9]利用能量算子解调法分别求解齿轮和轴承振动信号的幅值解调谱，并用于齿轮箱复合故障诊断。陈向民等[10]对角域的周期平稳信号进行能量算子解调分析，利用阶次解调谱提取故障特征。齿轮箱故障诊断实质是根据故障特征频率及其幅值变化识别故障，以上研究通过解调获取了故障特征频率，可初步判断故障类型和定位故障位置，但无法通过幅值的变化解释故障程度和调制强度之间的关系。为了更好地诊断故障的程度，有必要研究更精确的信号解调方法。

Qin[11]采用迭代能量算子解调和自适应低通滤波实现了多分量调幅调频信号的精确解调，比迭代希尔伯特变换和希尔伯特黄变换具有更高的精度，但其应用的对象均为欠调制信号，未针对过调制情况进一步讨论。Yang等[12]基于平方解调、贝塞尔函数和最小二乘优化算法，提出了一种抗噪性良好的高精度调幅调频信号分离方法。但缺点在于处理过调制信号时，调幅信号的分离误差较大，进而导致调频信号分离精度显著降低。由于无法保证实际故障振动信号一定是欠调制，上述方法的应用具有一定的局限性。

综上所述，提出了一种通用的齿轮故障振动信号的精确幅值解调方法。该方法基于齿轮故障振动的调制信号模型，利用希尔伯特变换构造优化目标函数，并用平方解调定义数学关系明确的约束方程，通过信赖域反射最小二乘优化算法[13]解得调幅信号的幅值和相位参数，可以在信号过调制时恢复真实的调幅信号，而且对于欠调制信号也有很好的适用性。

1 精确幅值解调重构方法

齿轮存在平稳型故障时，在第k阶啮合频率附近的齿轮振动调制信号可描述为[14]

xk(t)=Ak[1+bk(t)]cos[2πkfmt+θk+ck(t)]

(1)

(2)

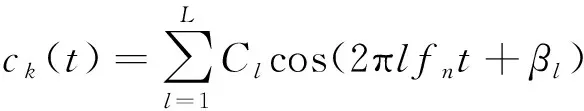
(3)

式中:Ak为第k阶啮合频率幅值，这里默认；fm为啮合频率；θk为第k阶啮合频率相位；bk(t)、ck(t)分别为第k阶啮合频率的调幅和调频函数；i、l为调制阶次；I、L为最大调制阶次；fn为故障齿轮转频；Bi、φi分别为第i阶调幅信号的幅值和相位；Cl、βl分别为第l阶调频信号的幅值和相位。

(4)

为方便描述，令阶次k，i，l=1，得到故障调制信号x1(t)如式(4)所示，并利用希尔伯特变换对其进行包络解调。

构造解析函数z(t)：

(5)

由此可得信号x1(t)的包络z(t)：

(6)

包络解调的局限性体现在：当幅值过调制，即|B1|>1时，包络z(t)为原低频调幅信号的绝对值，即低频调幅信号幅值在零线以下的部分将被翻折至零线上方，如图1所示。此时的包络的频谱图2中将包含故障特征频率fn的各阶次谐波分量。

图1 希尔伯特包络

图2 希尔伯特包络频谱

由此引出所提方法的核心思想：对待定系数的故障调制数学模型进行希尔伯特变换得到包络数学模型，并通过信赖域反射最小二乘优化算法求解包络数学模型的幅值和相位参数，以实现包络数学模型与实际故障振动信号包络的最优匹配。无论实际故障振动信号是过调制还是欠调制，利用包络模型参数重构的调幅信号都能正确表示故障振动信号的真实调幅。

该方法由带通滤波和频谱校正、优化方程构造、待定系数求解三大部分组成，流程如图3所示。

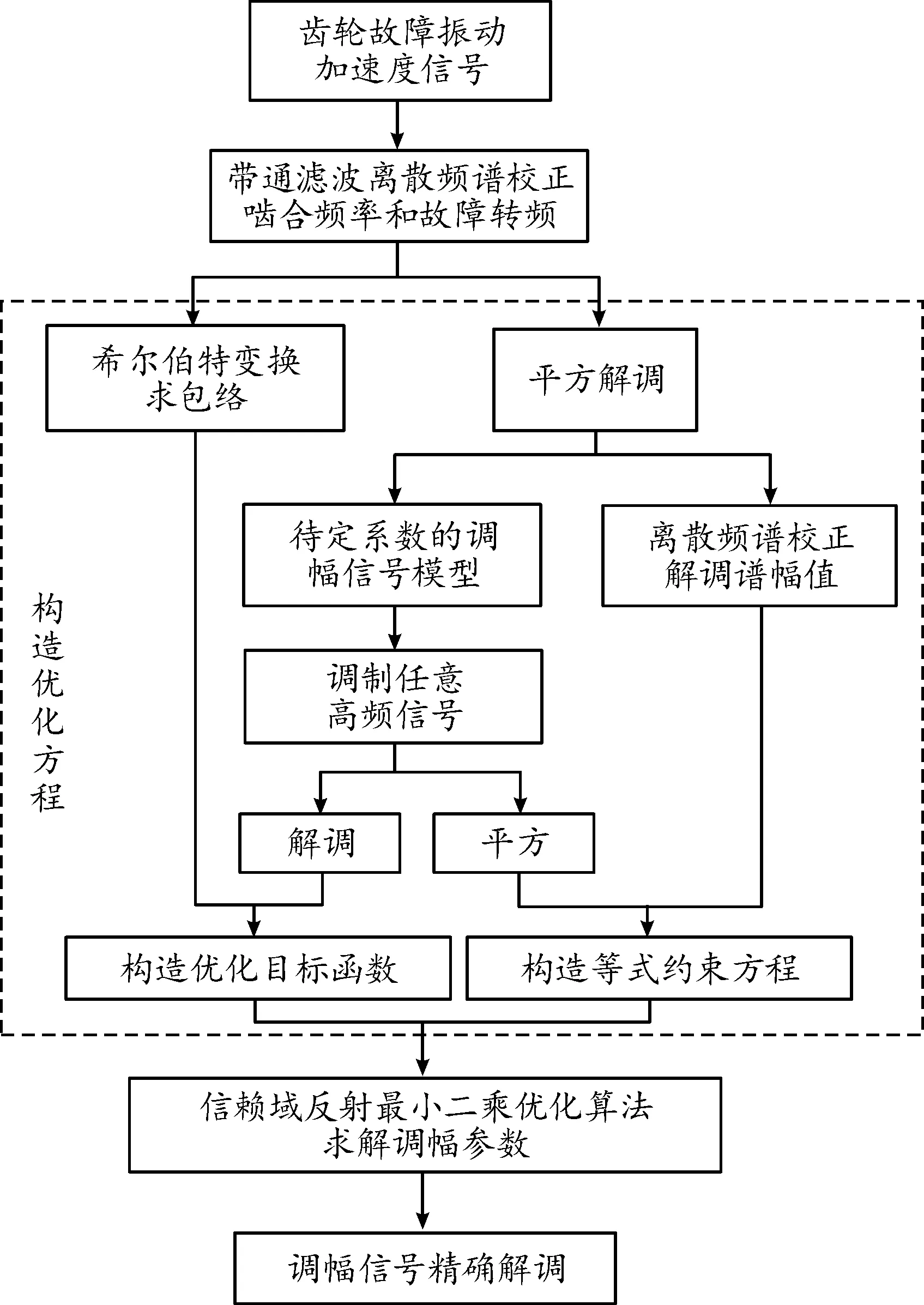
图3 方法流程框图

1.1 带通滤波和频谱校正

1) 通过等间隔采样获取存在平稳型故障的定轴齿轮箱在轴承座处的振动加速度信号。

2) 对振动加速度信号进行带通滤波，选取远离共振峰的某阶啮合频率为滤波器中心频率，并使滤波器通带覆盖此阶啮合频率两侧的故障频率调制边带。滤波后得到具有调幅调频特征的故障振动信号x(t)。

3) 由于齿轮实际振动信号为包含噪声的复杂多分量信号，信号采样过程中难以做到整周期采样，需要利用加汉宁窗的比值校正法[15]对信号x(t)进行频谱校正，以获取校正的故障特征转频fnc和校正的啮合频率fmc。

1.2 优化方程构造

1) 构造优化目标函数：包络数学模型与实际故障振动信号的包络的误差平方和最小。

① 结合频谱校正的结果，构造调幅模型yl(t)：

(7)

式中：a为待定的啮合频率幅值；bi、βi分别为待定的各阶调制谐波的幅值和相位；Imax为待定的最大谐波调制阶次；fnc为校正的故障齿轮转频。

根据平方解调的原理，对故障调制信号取平方，只保留不含高频载波的低频部分。无论信号是欠调制或过调制，低频部分中都只包含直流分量、调制频率基频的谐波和调制频率2倍频的谐波[3]。故可根据故障振动信号x(t)平方解调谱中实际出现的最高调制阶次(记为2Imax)确定调幅信号模型的调制阶次Imax。

② 用yl(t)调制已知的任意高频(该方法选取校正后的啮合频率fmc)谐波信号yh(t)，得到待定系数的故障调制数学模型y(t)

(8)

③ 利用希尔伯特变换对y(t)进行包络解调，得到待定系数的包络模型yenv(t)

(9)

④ 确定优化的目标函数为：待定系数的包络模型yenv(t)与故障振动信号的包络z(t)的误差平方和最小，即

(10)

2) 为了进一步提高待定系数的求解精度，加入等式约束方程：故障振动信号x(t)平方解调谱中故障转频及其倍频处的校正幅值与故障调制模型y(t)取平方得到的对应频率处的幅值表达式相等。

① 利用加汉宁窗的比值校正法对信号x(t)的平方解调谱进行幅值校正，得到零频、故障转频及其倍频处的校正幅值Akfnc(k=0，1，2，…，2Imax)。

② 对式(8)所示的故障调制数学模型y(t)取平方，归纳零频、故障转频及其倍频kfnc(k=0，1，2，…，2Imax)处的幅值表达式akfnc见表1。

表1 幅值表达式

③ 令故障振动信号x(t)平方解调谱的校正幅值与幅值表达式对应相等，构造等式约束方程为

Akfnc=akfnc

(11)

1.3 待定系数求解

2) 确定待定系数的求解初值：调制信号幅值和相位求解初值分别设为0.1和1。

3)式(7)所示调幅模型中的待定系数(a，b1，…，bImax，β1，…，βImax)共2Imax+1个，式(11)确定的等式约束方程个数也为2Imax+1个。利用信赖域反射最小二乘优化算法[13]求解目标函数，得到待定系数，完成故障振动信号x(t)的精确幅值解调和调幅信号重构。

若故障振动信号同时存在多个转频调制，可分别对每个故障转频进行调制阶次的判断和目标函数、约束方程的构造，该方法依然适用。

2 仿真分析

2.1 仿真一

为验证所提方法的通用性，给出一阶欠调制仿真信号1x1(t)和一阶过调制仿真信号2x2(t)为

x1(t)=3[1+0.6cos(2π14t+30°)]cos(2π360t)

(12)

x2(t)=2[1+1.5cos(2π10t+45°)]cos(2π360t)

(13)

设置采样频率fs=1 024 Hz，采样点数N=1 024。由于给定的仿真信号均为单分量信号，且满足整周期采样的要求，可以省略所提方法中带通滤波和离散频谱校正的步骤。直接对仿真信号进行平方解调，图4平方解调谱显示2个调制频率(10、14 Hz)的最高阶次均为2阶，根据1.2节分析，可将调幅信号数学模型的阶次定为2/2=1阶，如式(14)所示。

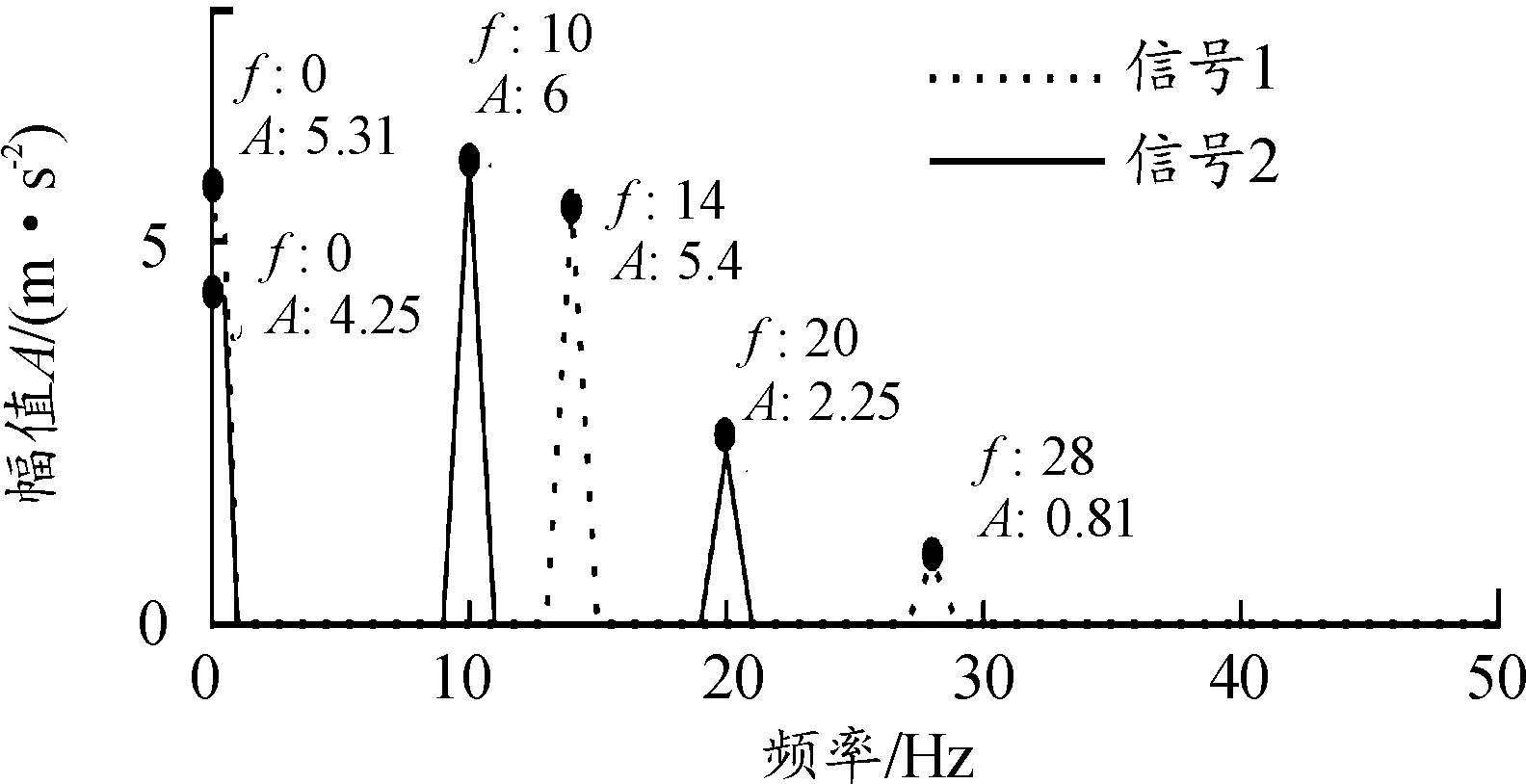
图4 平方解调谱

y1(t)=a·[1+bcos(2πft+β)]

(14)

式中：a为待定载波信号幅值；b为待定调制信号幅值；f为调制频率；β为待定调制信号相位。

由于无需频谱校正，读出图4平方解调谱中零频、调制频率、调制频率2倍频处幅值见表2。

表2 平方解调谱幅值

对仿真信号1做希尔伯特变换得到包络信号z1(t)，按式(10)构造优化目标函数，并按式(11)添加平方解调谱幅值与幅值表达式对应相等的约束方程，得到优化方程见式(15)。利用信赖域反射最小二乘优化算法求解式(15)，得到调幅信号待定系数。同理可求得仿真信号2的调幅信号待定系数。

(15)

仿真信号1、信号2的调幅信号待定系数求解结果及误差如表3所示，欠调制信号的幅值参数求解误差最大仅为0.5%，相位参数求解误差仅为0.04%，过调制信号参数求解没有误差。

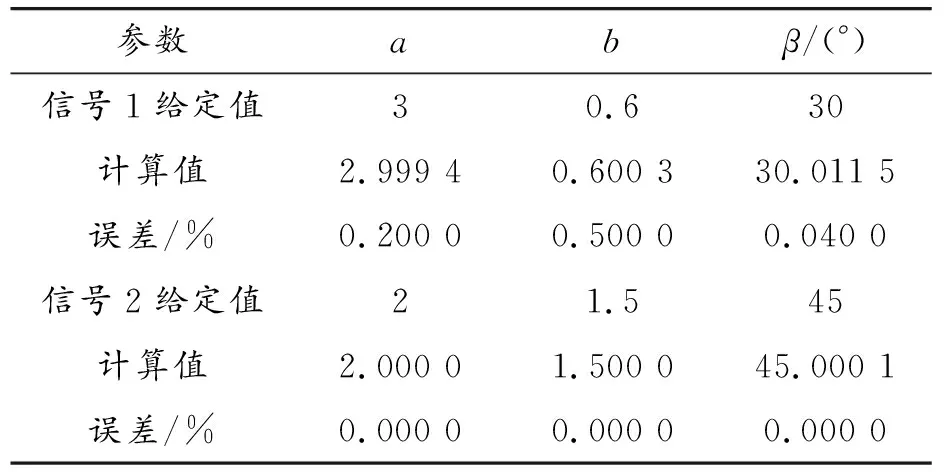
表3 调幅信号待定系数求解结果及误差

将上述求解的幅值和相位参数代入式(14)重构调幅信号。从图5可见，信号1的包络与解调重构的调幅信号的时域波形和频谱完全重合。从图6可见，解调重构的调幅信号的时域波形有过零部分，其频谱只有零频和一阶调制频率且其幅值与给定值相等，说明此时重构出的信号是真实的调幅信号；而信号2的包络时域波形不再是真实的调幅信号，是把调幅信号零线下的部分翻折到了零线上方，且包络频谱中出现了调制频率的高阶倍频。

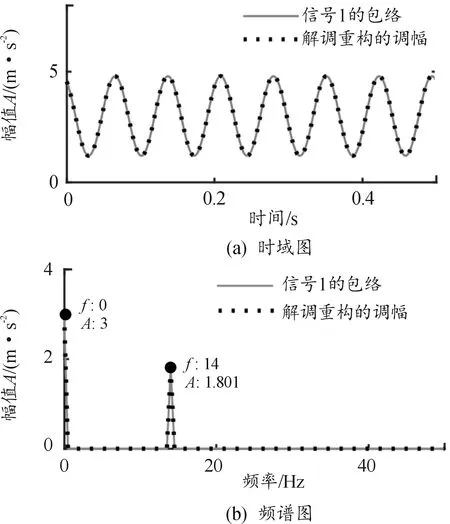
图5 欠调制仿真信号1解调重构结果

图6 过调制仿真信号2解调重构结果

以上仿真充分说明了该方法在信号欠调制和过调制时均实现了真实调幅信号的精确解调重构，具有通用性。

2.2 仿真二

为验证所提方法对于多频率调制振动信号的解调效果，同时加入不同信噪比的白噪声来检验其抗噪性。仿真二选取文献[12]基于平方解调和最小二乘优化算法的幅值解调法(方法二)和文献[2]希尔伯特变换解调法(方法三)作对比。

设置齿轮箱输入轴、输出轴齿轮齿数分别为24、56，输入转速为906 r/min，采样频率fs为4 096 Hz，采样时长T为2 s。给出无噪声过调制仿真信号x(t)：

x(t)=2[1+0.6cos(2πfn1t+45°)+

1.4cos(2πfn2t+36°)+

1.2cos(4πfn2t+30°)]×

cos[2πfmt+45°]

(16)

式中:输入轴齿轮转频fn1为15.1 Hz、啮合频率fm为362.4 Hz、输出轴齿轮转频fn2为6.47 Hz。

用上下截止频率分别为420 Hz和300 Hz的带通滤波器处理仿真信号，得到啮合频率及其附近的调制边带，频谱图如图7所示。利用加汉宁窗的比值校正法得到校正的啮合频率fmc、输入轴转频fn1c、输出轴转频fn2c分别为362.396 7、15.075 5、6.485 1 Hz。对带通滤波后的仿真信号进行平方解调，其平方解调谱如图8所示，其中fn1和fn2的最高调制阶次分别为2阶、4阶，根据1.2节的分析，将调幅信号数学模型中fn1和fn2阶次分别定为 2/2=1阶、4/2=2阶，得到式(17)所示的调幅信号模型y2(t)。

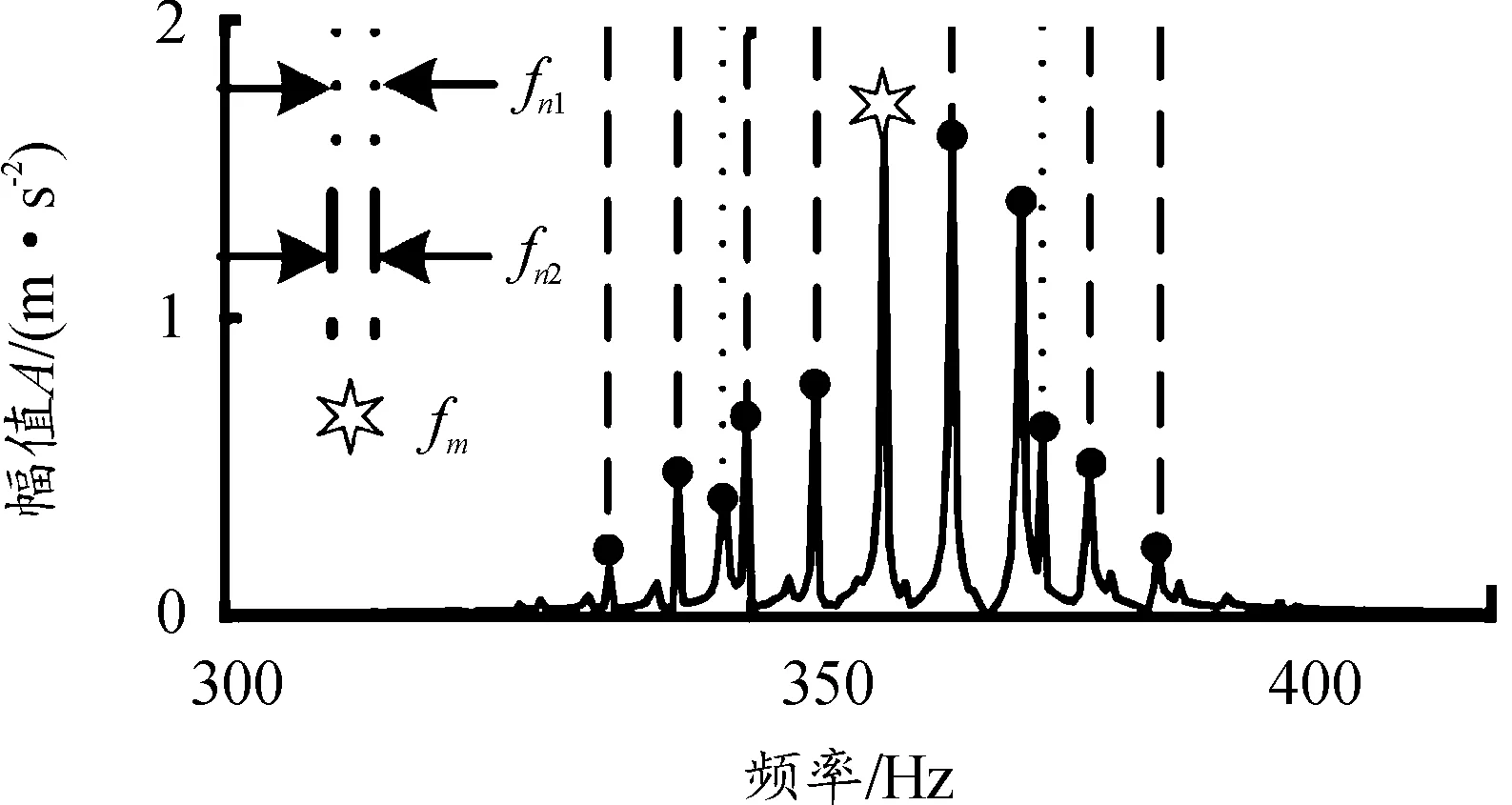
图7 过调制仿真信号

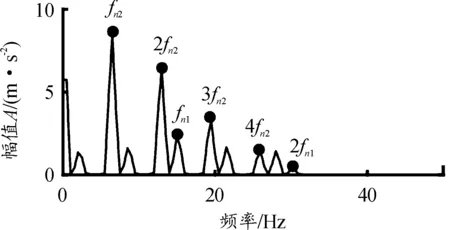
图8 平方解调谱

y2(t)=a[1+b1cos(2πfn1ct+β1)+

b2cos(2πfn2ct+β2)+

b3cos(4πfn2ct+β3)]

(17)

用比值校正法校正平方解调谱中零频、故障转频及其倍频(fn1、2fn1、fn2、2fn2、3fn2、4fn2)的幅值，得到校正幅值Akfnc见表4。

表4 平方解调谱的校正幅值

(18)

对滤波后的仿真信号做希尔伯特变换得到包络信号z2(t)，按式(10)构造目标函数，并添加按式(11)构造的约束方程，得到优化方程如式(18)所示。利用信赖域反射最小二乘优化算法求解式(18)，得到待定系数及误差见表5。

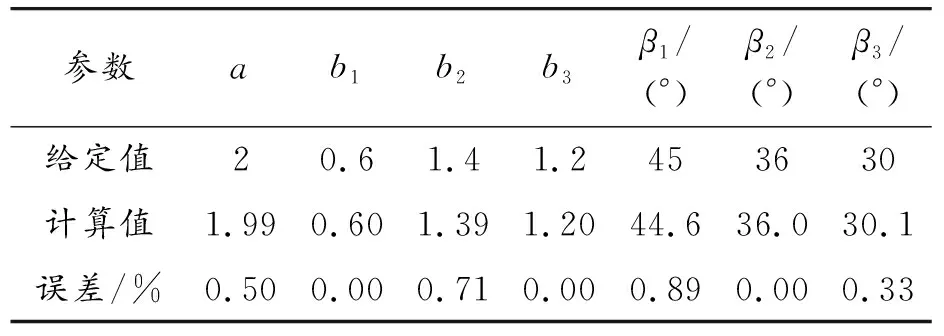
表5 调幅信号待定系数及误差

从表5可看出无噪声条件下，该方法对于过调制信号的解调达到了很高的精度，最大幅值求解误差为0.71%，最大相位求解误差为0.89%。

图9为过调制求解结果对比图，可以看出：① 解调重构的调幅信号有过零线的部分，说明仿真信号中存在过调制现象；② 该方法解调重构的调幅信号与仿真信号的真实调幅保持了高度一致。

图9 求解结果对比

根据1.2节的分析，用解调重构的调幅信号y2(t)调制啮合频率载波，再对其进行解调，得到解调重构的包络yenv(t)。图10为仿真信号的包络z2(t)和解调重构包络yenv(t)的频谱对比图，由于存在过调制，频谱中不仅有给定的故障调制频率，还出现了故障调制频率的更高阶倍频及2个故障调制频率的差[3]，且两信号在各个频率处幅值都基本相等。以上结果表明，振动信号有多个频率调制的情况下，该方法也能实现真实调幅信号的精确重构。

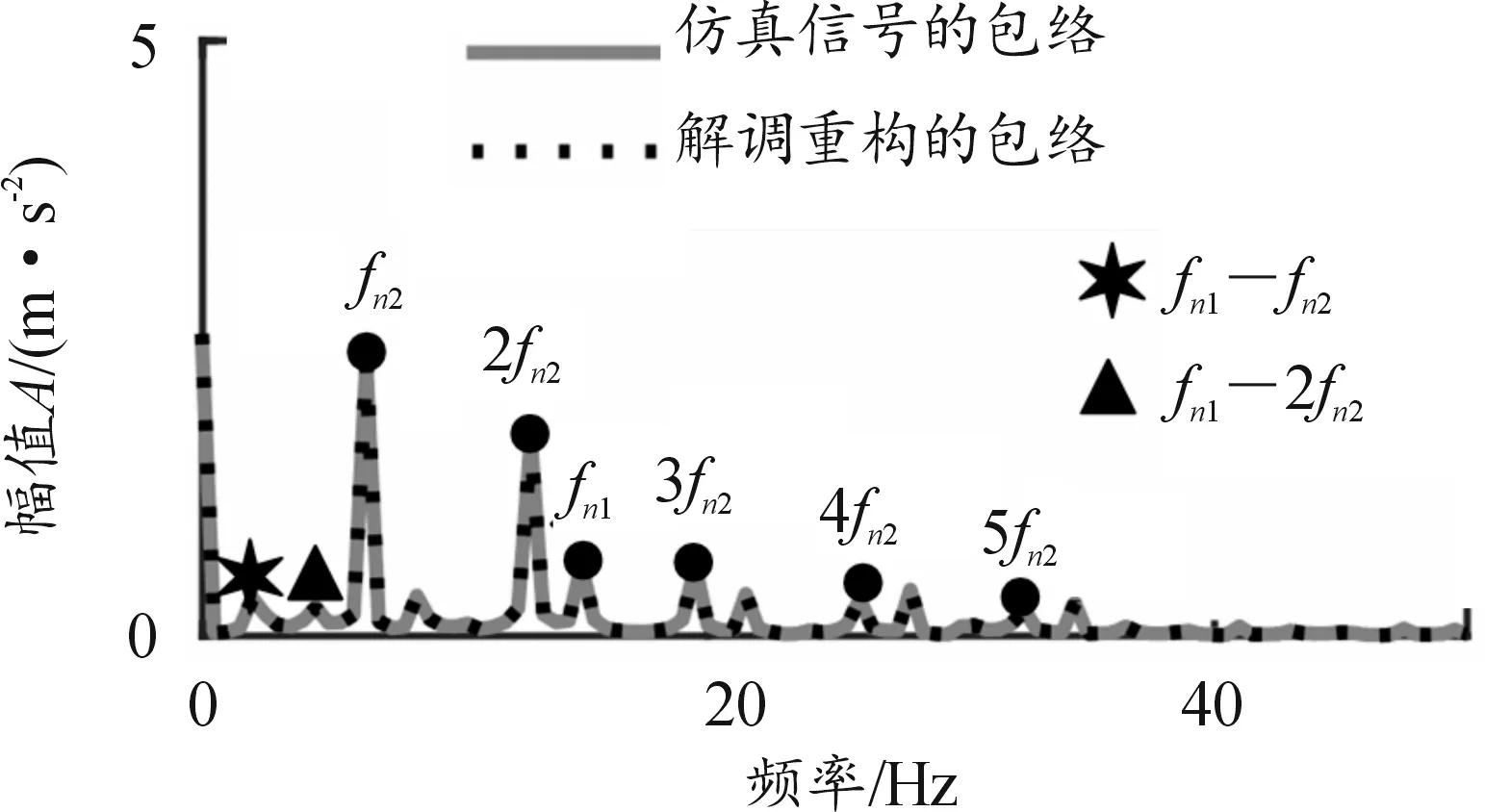
图10 希尔伯特包络频谱

为进一步验证该方法的抗噪性，在仿真信号中分别添加信噪比为10、5、2 db的高斯白噪声，分别利用该方法和方法二、三求解调幅信号待定系数20次，取20次计算结果的平均误差，见表6。

由表6可知，随着信号信噪比降低，该方法和方法二求解误差都变大，方法三求解误差变化不明显，但该方法求解精度明显好于方法二、三。加2 db白噪声时该方法的幅值求解误差仍可以控制在5%范围内，出现的最大相位求解误差约为15.2%。而方法二在10 db小噪声时的幅值和相位求解精度已经很差，2 db噪声时相位求解误差更是达到了130%，已经不适合用于求解过调制信号。方法三求解精度差的原因在于希尔伯特变换解调过调制信号时，包络频谱会出现高于实际调制阶次的频率成分，使频谱能量分散，故在实际调制阶次处的幅值误差较大。综上所述，该方法在解调过调制信号时有明显的优越性和良好的抗噪性。

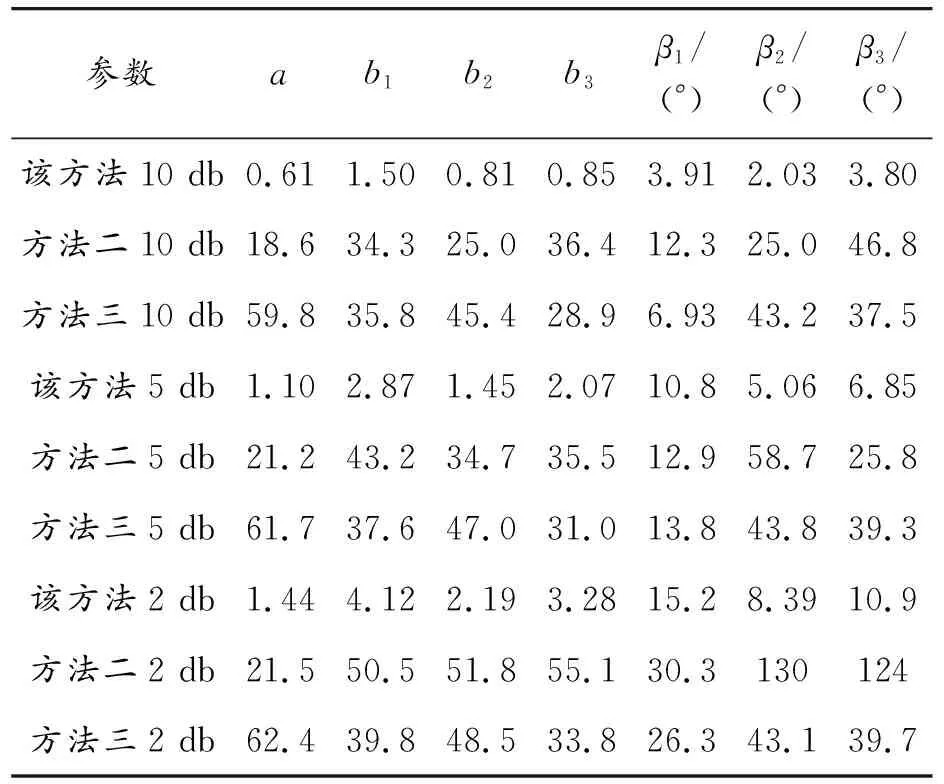
表6 不同信噪比过调制信号待定系数平均误差

3 实验验证

实验对象为单级定轴齿轮箱，输入轴、输出轴齿轮齿数分别为24、56，传动实验平台设备布置如图11所示。由于弹性联轴器的存在，传动系统不可避免地存在轴不对中，采用瑞典的激光对中仪TKSA51测量齿轮轴的不对中量。实验中将4个传感器分别布置于输入轴和输出轴的轴承座上，采用姆勒贝姆(Müller-BBM)数据采集系统采集振动加速度信号，设置采样频率为51 200 Hz，采样时长2 s。实验一、二为输出轴不对中的平稳型故障实验，齿轮箱输入转速1 000 r/min，负载200 N·m。2次实验前分别测得输出轴不对中量为0.18 mm和1.35 mm。实验三为输出轴齿轮断齿、输入轴不对中实验，分别给定输入转速800 r/min、负载0 N·m和输入转速1 200 r/min、负载50 N·m。实验前测得输入轴、输出轴不对中量分别为0.38、0.05 mm。

图11 传动实验平台设备布置

3.1 实验一：轻微平稳型故障实验

采集输出轴轴承座(测点1)处的振动加速度信号，选取边频带分布清晰的第三阶啮合频率(记为fm)为滤波器中心频率，用上下截止频率分别为1 250、1 150 Hz的带通滤波器处理实验信号。滤波后信号的频谱如图12所示，可以发现啮合频率两侧主要出现了输出轴转频fn2及其高阶倍频调制的多阶边带，此外也有一阶输入轴转频fn1调制的小幅值边带。说明输出轴存在更加明显的不对中现象，考虑输入轴属于正常的对中误差，这与故障设置相一致。

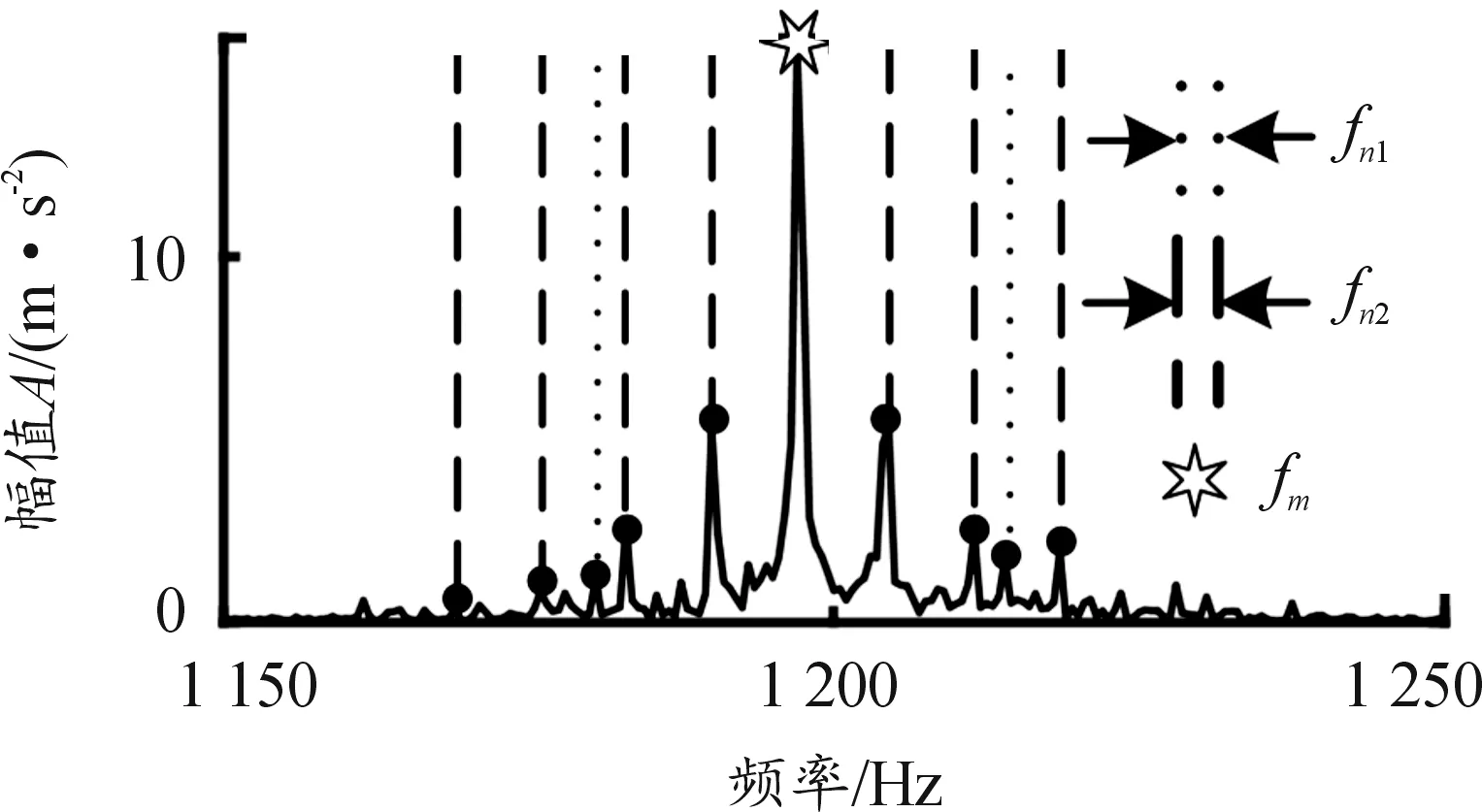
图12 滤波后信号频谱

y(t)=20.41[1+0.14cos(2πfn1ct)+

0.41cos(2πfn2ct+4.20)+

0.13cos(4πfn2ct+4.07)+

0.06cos(6πfn2ct+1.27)+

0.05cos(8πfn2ct+2.09)]

(19)

利用比值校正法得到校正后的第三阶啮合频率fmc、输入轴转频fn1c、输出轴转频fn2c分别为1 199.036 4、16.709 0、7.112 4 Hz。从图13平方解调谱判断fn1、fn2调制阶次分别为2/2=1阶、8/2=4阶，应用所提方法得到解调重构调幅信号，见式(19)。

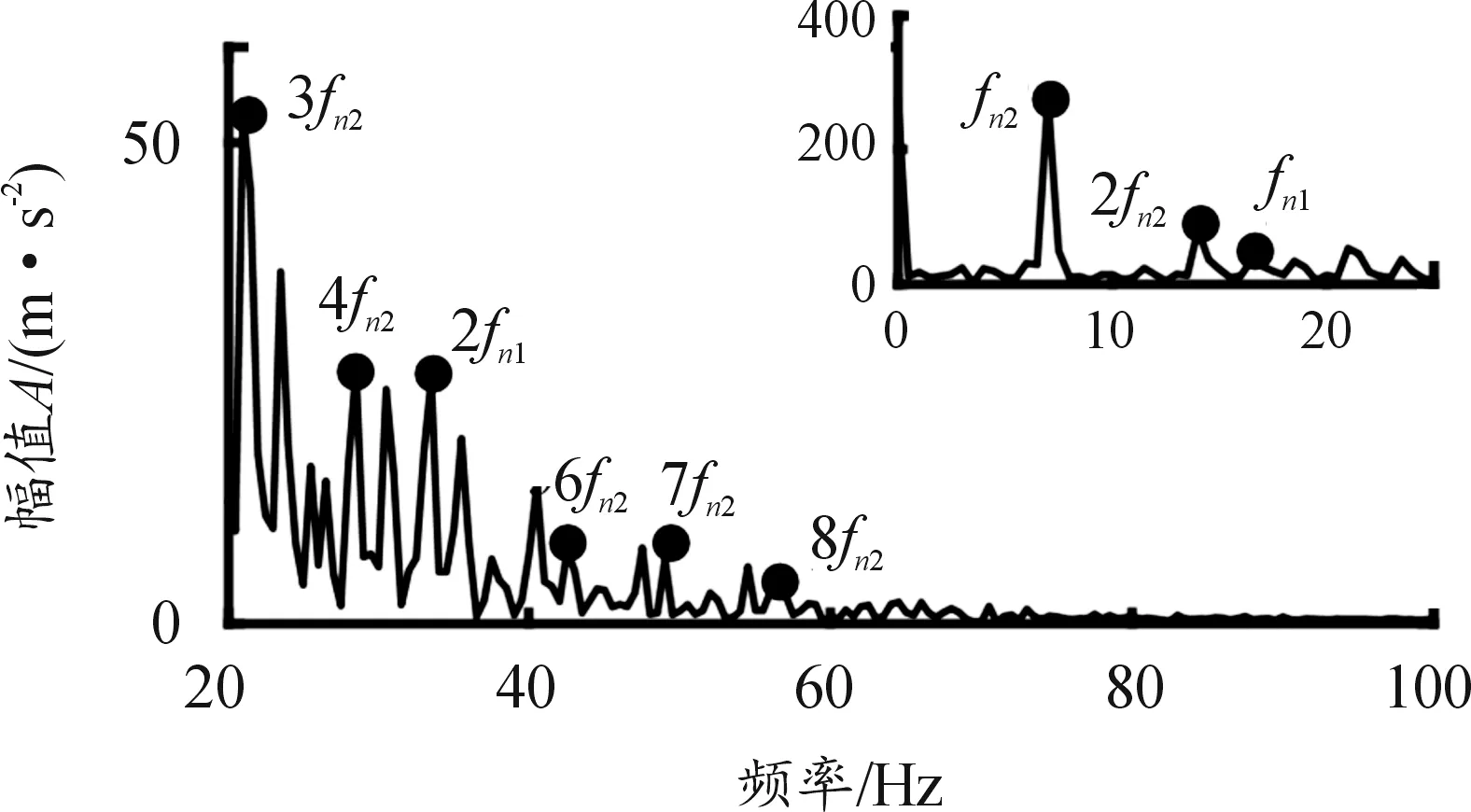
图13 平方解调谱

解调重构结果如图14所示，可以发现：① 图14(a)中解调重构的调幅信号全部在零线以上，说明此状态下实验信号为欠调制。解调重构的调幅信号与实验信号的包络时域波形吻合度很高，区别在于实验信号的包络中存在更高频的波动，考虑其原因为：平方解调谱中调制频率的高倍阶次处的幅值相比于基频很小，更容易被噪声淹没，可能导致人为判定的调幅信号阶次稍微偏低。② 由图14(b)可见，虽然实验信号的包络存在更高阶调制倍频，但其幅值相比于零频和调制基频基本可以忽略，可认为实验信号的包络能量主要集中于零频和低阶调制频率(fn1、fn2、2fn2、3fn2、4fn2)处，且在这些频率处解调重构的调幅信号幅值误差很小。该方法的解调效果良好。

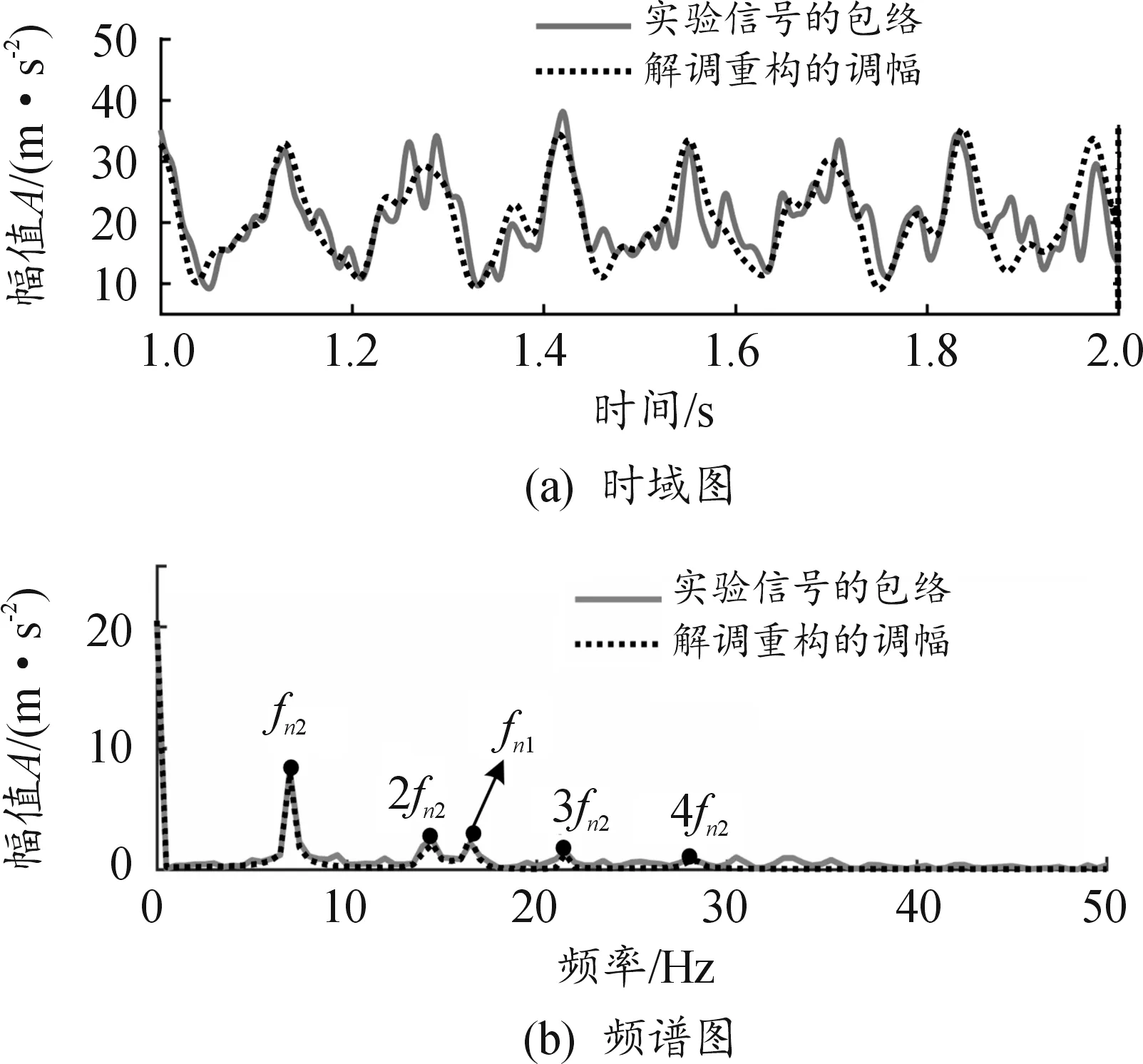
图14 信号解调重构结果

3.2 实验二：严重平稳型故障实验

同样采集测点1处的振动信号并用与实验一相同的滤波器进行带通滤波，用所提方法处理滤波后的信号得到解调重构的调幅信号，见式(20)。

y(t)=13.20[1+0.18cos(2πfn1ct+2.21)+

1.37×cos(2πfn2ct+1.21)+

0.61cos(4πfn2ct)+0.21×

cos(6πfn2ct+0.87)+

0.19cos(8πfn2ct+0.28)]

(20)

实验二信号解调重构的结果如图15所示，可以发现：① 图15(a)中，解调重构的调幅信号有明显的过零部分，说明实验信号存在过调制。而实验信号的包络没有出现严格过零点，考虑其原因为：解调重构的调幅信号不包含噪声，而实验信号受到噪声影响，振动信号和噪声的矢量叠加使振动信号原过零点处的幅值不再为零。② 图15(b)中，解调重构的调幅和实验信号包络的频谱出现了明显差异，前者表示实验信号的真实调幅，仅在零频和解调重构的调制频率(fn1、fn2、2fn2、3fn2、4fn2)处有幅值；而后者由于过调制，频谱中出现了更高阶调制倍频，且明显存在2个调制频率的差。

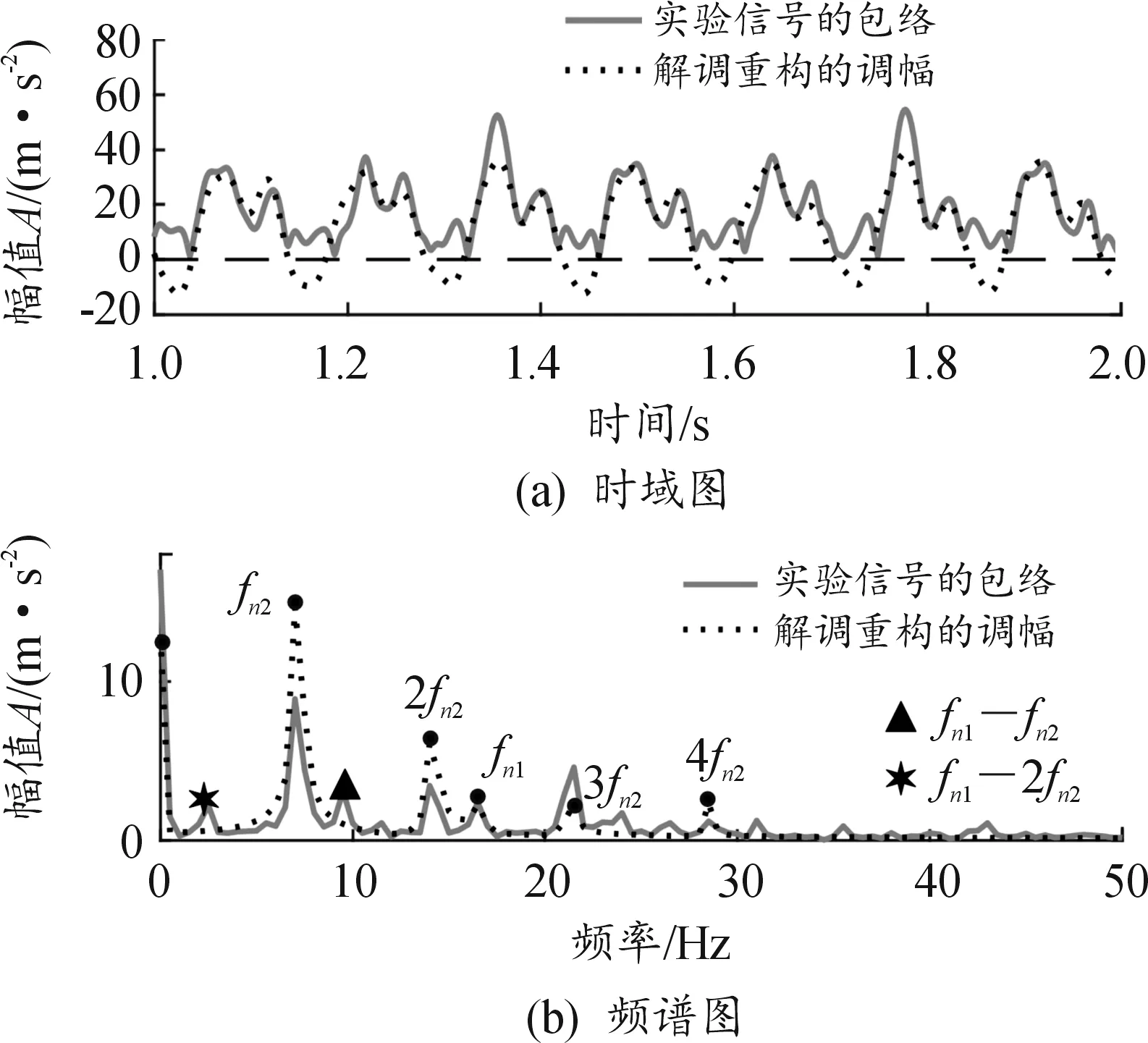
图15 信号解调重构结果

实验一、二的解调结果对比可知：① 齿轮箱存在轻微不对中时振动信号表现为欠调制，大的不对中量则会导致振动信号过调制。② 虽然实验一解调重构的调幅信号的调制阶次与实验二相同，均为输入轴1阶、输出轴4阶，但两者在调制强度上存在很大差异，若按传统的解调方法得到齿轮故障调制频率，只能定位故障位置，无法准确判断故障程度。该方法可以通过精确幅值解调来量化调制系数，说明了该方法在精确故障诊断方面的优越性。

3.3 实验三：输出轴齿轮断齿、输入轴不对中实验

输入转速800 r/min和1 200 r/min 2种工况下的振动响应信号频谱分别如图16、图17所示。800 r/min时，齿轮第一阶啮合频率(320 Hz)附近无明显共振峰；1 200 r/min时，齿轮第二阶啮合频率(960 Hz)与1 200 Hz附近的共振峰存在耦合。分别在上述两阶啮合频率附近进行带通滤波，利用所提方法求出调幅参数,见表7、表8。

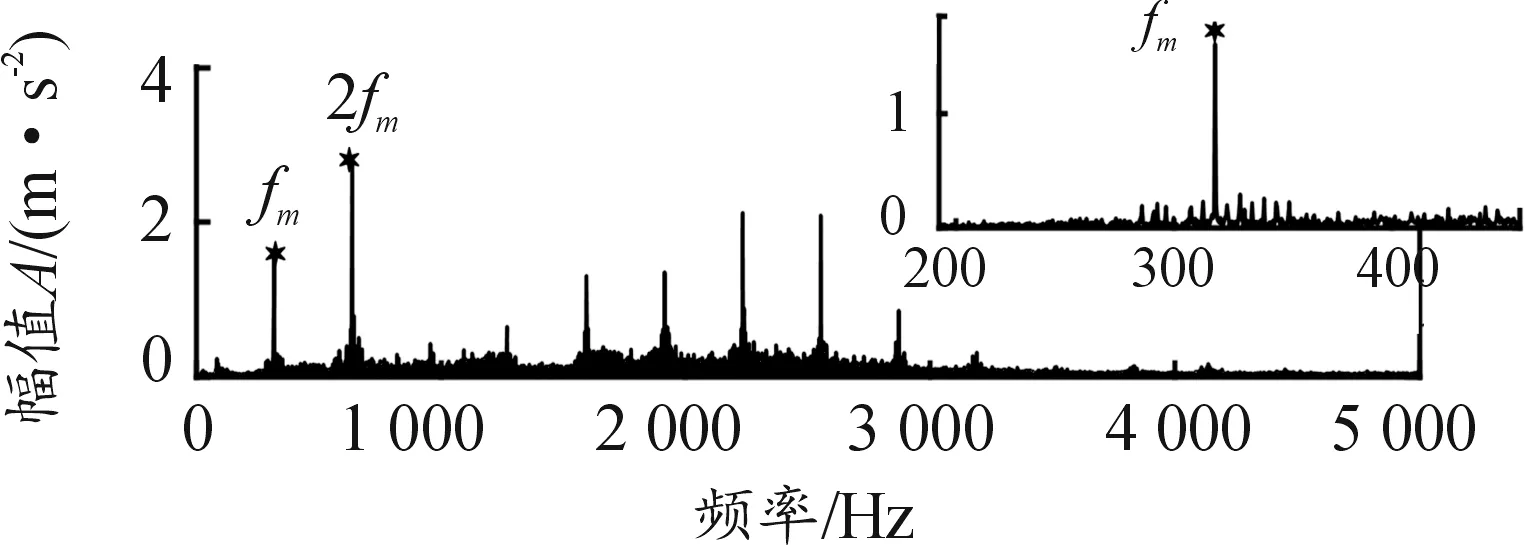
图16 800 r/min振动响应频谱

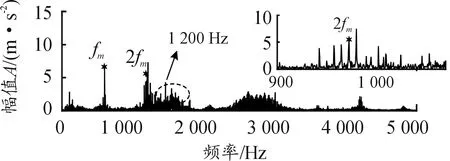
图17 1 200 r/min振动响应频谱

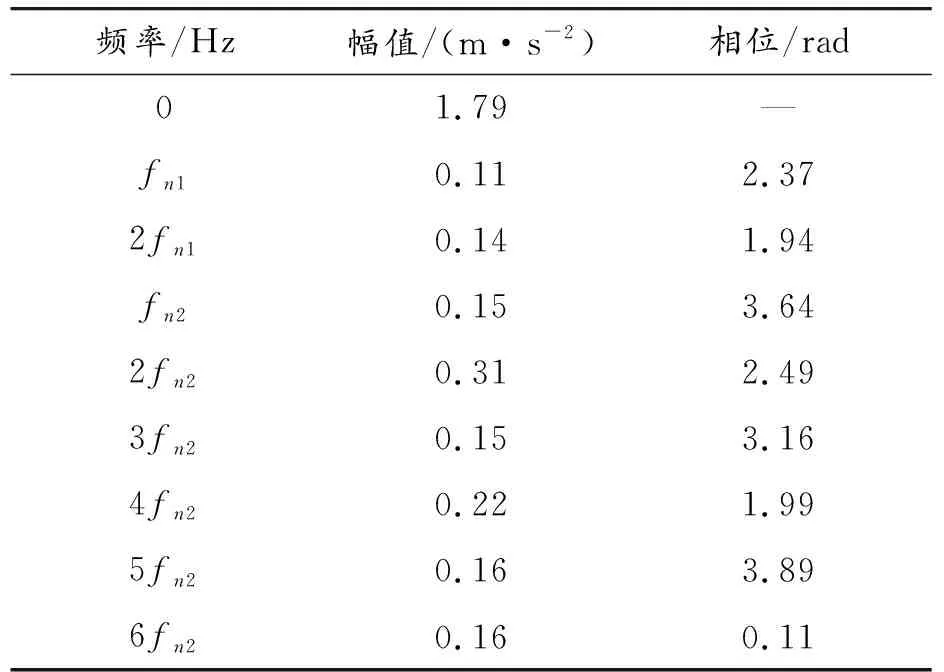
表7 800 r/min调幅参数

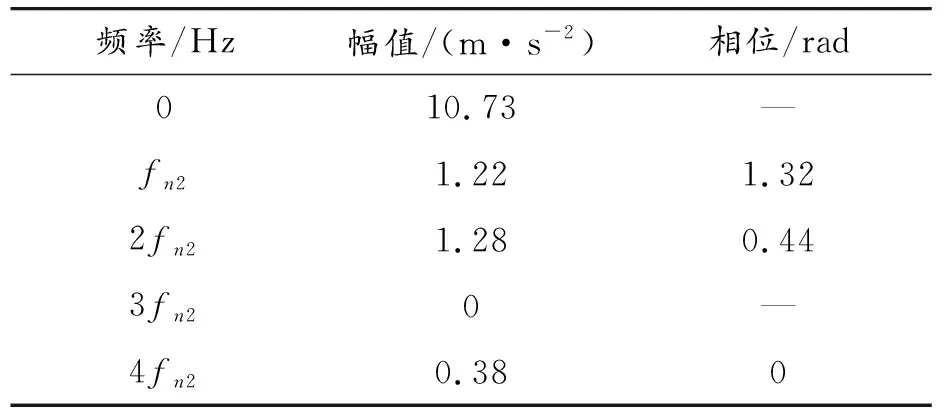
表8 1 200 r/min调幅参数

解调结果显示，800 r/min时第一阶啮合频率附近有2阶输入轴转频调制、6阶输出轴转频调制，且输出轴转频谐波的幅值较小；1 200 r/min时第二阶啮合频率附近只有3阶输出轴转频调制，阶次少但调制强度大。

实验三主要是输入轴不对中，但2种工况下的解调信号都是输出轴转频阶次明显高于输入轴，原因在于：周期性断齿冲击激励容易激起系统共振峰且全频带内都会产生以断齿齿轮转频为间隔的离散谐波成分，由于啮合频率是齿轮转频的整数倍，这些以断齿齿轮转频为间隔的离散边带会延伸到啮合频率两侧并产生调制现象。另外，啮合频率靠近共振峰会导致振动信号的调制强度变大。

用解调重构的调幅信号乘以啮合频率的载波，再对其进行希尔伯特解调，得到解调重构的包络信号。图18显示，800 r/min时在求出的2阶输入轴转频和6阶输出轴转频处，两包络信号重合度较高。由表8可知，1 200 r/min时重构的调幅信号会有过零点，其经过调制解调后得到的重构包络信号频谱将有输出轴转频fn2的多阶倍频。图19显示在前4阶输出轴转频处，解调重构的包络与实验信号包络的幅值基本吻合。

图18 800 r/min包络信号对比

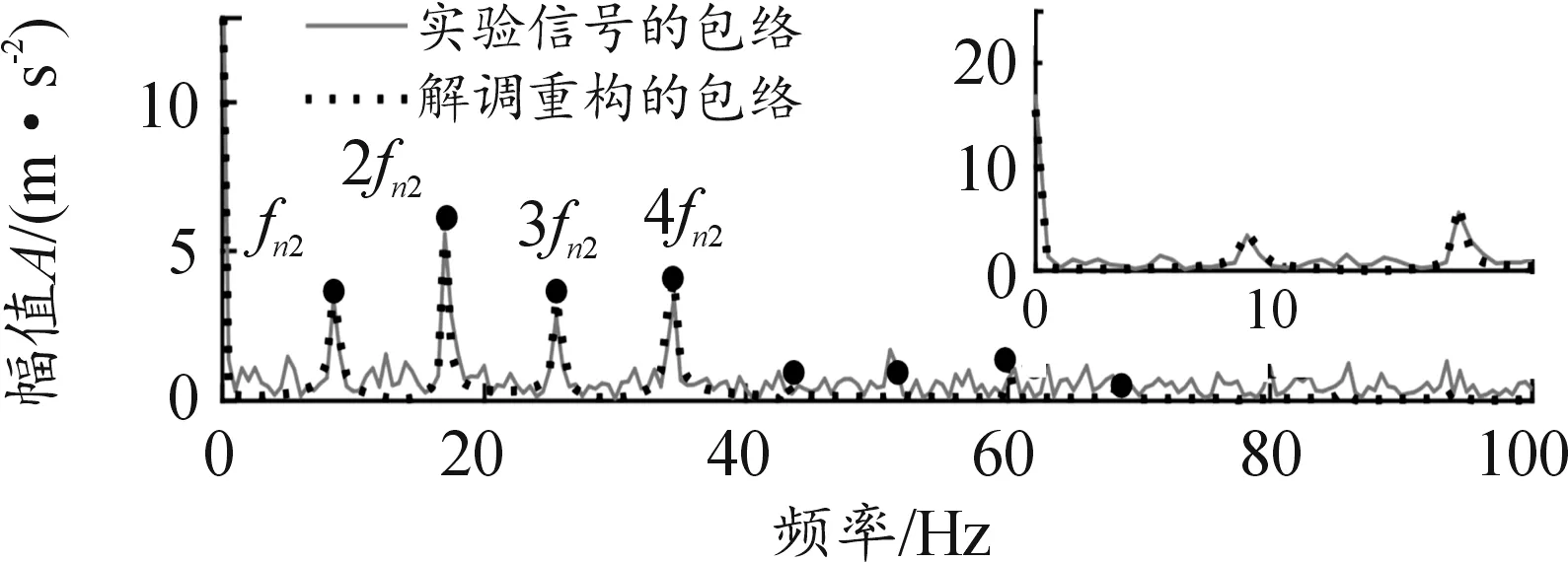
图19 1 200 r/min包络信号对比

综上，啮合频率或其倍频附近的振动信号分别在非共振区、共振区取得了良好的解调效果，验证了该方法用于处理断齿冲击型故障的有效性。

4 结论

提出了一种齿轮故障调制信号的精确幅值解调方法。利用希尔伯特变换构造优化目标函数，并加入基于平方解调构造的约束方程，最后用信赖域反射最小二乘优化算法求解调幅参数，实现了过调制情况下真实调幅信号的解调重构，同时对欠调制信号也具有适用性。实验表明，齿轮出现轻微平稳型故障时振动信号表现为欠调制，严重故障则会导致振动信号出现过调制。断齿故障导致全频带内产生的离散谐波成分会影响啮合频率附近振动信号的调制强度。该方法处理平稳型和断齿冲击型实验信号均取得了良好的解调效果，且根据平稳型故障时解调结果的差异可以判断齿轮箱的故障程度。该方法的具体优点如下：

1) 拓展了基于希尔伯特变换解调幅的适用范围，既可用于处理欠调制信号，也可用于处理过调制信号，具有通用性。

2) 解调精度高。仿真表明在无噪声条件下，求解一阶欠调制信号的幅值参数最大误差为0.5%，相位参数误差为0.04%；求解一阶过调制信号时幅值和相位参数无误差，求解多阶过调制信号时最大幅值和相位误差不超过1%。

3) 抗噪性好。与现有的基于平方解调和最小二乘优化算法的幅值解调方法(方法二)和希尔伯特变换解调法(方法三)作对比。仿真表明，加入信噪比2 db的白噪声后，过调制时该方法幅值参数和相位参数的最大求解误差分别为4.12%、15.2%；方法二幅值参数最大求解误差为55.1%，相位求解误差更是达到了130%；方法三幅值和相位的最大求解误差分别为62.4%和43.1%。