在数学实验中营造“思维场”

孔维富

[摘 要]思维是数学能力之 “核”， 也是核心素养之 “魂”。 以“三角形边的关系”为例，提出在实验中发展学生数学思维的方法，即为学生发展创造平台，给予学生思考的时空，使数学实验成为一种必需，实现学生思维品质的提升。

[关键词]数学实验;思维;三角形边的关系

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）29-0070-02

思维是数学能力之 “核”， 也是核心素养之 “魂”。美国教育家杜威曾言：“学习就是要学会思维，教育的目的不是学会知识，而是习得一种思维方式。”小学数学教学应具有双重任务，一是传授学生基本的数学知识和技能，二是教给学生数学的思维方法，而后者往往在学生的数学学习和长远发展中起着决定性作用。实验教学法作为一种新型的教学方法就能够真正渗透数学的思维方法。 然而，在实验教学中，出现了重操作、轻思考，重结果、轻过程的倾向。笔者结合自身教学经验，以“三角形边的关系”为例，探索在实验教学中发展学生数学思维的方法和路径，以期能够起到抛砖引玉的效果。

一、在认知分歧处思考，使数学实验成为一种必需

小学生对于数学知识的学习和理解离不开原有的生活经验和认知基础。在学习新知识之前，学生已经在日常生活中积累了一定的生活经验，而这些生活经验或许具有一定的“感性色彩”，未必是正确的，但这些生活经验却构成了学生学习新知识的基础。在教学中，教师可创设情境，激活学生的已有经验，引发学生思维冲突，使学生产生一探究竟的欲望和决心，从而使数学实验成为学生的一种内在需求。

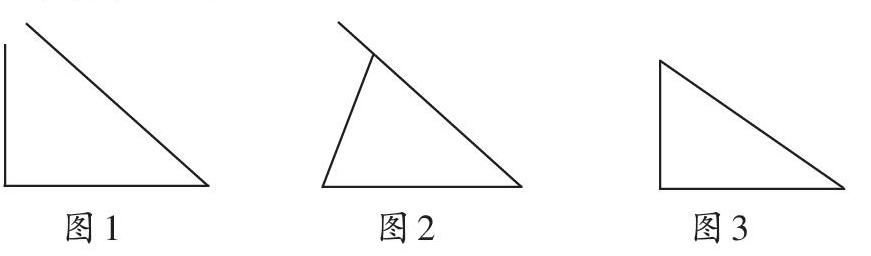
师：我们已经初步认识了三角形，那么什么是三角形呢？

生1：三条线段首尾顺次相接围成的图形叫三角形。

师：什么叫首尾顺次相接呢？图1可以吗？

生2：这样不行，首尾顺次相接围成的肯定是个封闭图形。

师：那图2呢？

生3：这样也不行。

师：图3呢？

生4：像图3这样围成的图形才是三角形。

师：通过图形不难看出，三角形由三条线段首尾顺次相接围成。那么，请同学们思考，是不是任意三条线段都能围成三角形呢？

师：现在，请同学们从学具袋中任意拿出三根小棒拼一拼，看看能不能拼成三角形。

（有的学生用三根小棒拼成了三角形，而有的学生却没有拼成）

师：为什么都是用三根小棒，有的能拼接成功，而有的却不能呢？

生5：我认为这跟三根小棒的长度有关系。

生6：我认为只跟最长的那根小棒的长度有关系。

生7：我认为跟最短的那根小棒的长度有关系。

……

师：“实践是检验真理的唯一标准。”现在，就让我们通过严谨的数学实验来验证猜测。

教学中，教师首先引导学生回顾了三角形的内涵，在此基础上引导学生对“是不是任意三条线段都能围成三角形？”这一问题展开思考。学生通过操作发现，有的小棒能围成三角形，有的却不能，进而引发了学生认知上的冲突和矛盾，激发了学生学习新知的强烈欲望，此时，教师引出数学实验变得水到渠成。

二、在探究中思考，为学生发展创造平台

苏霍姆林斯基曾言：“在人的内心深处，都有一种根深蒂固的需要，这就是希望自己是一个发现者、研究者和探索者，而在儿童的内心世界中这种需要尤为强烈。”学习本来就是一个主动探究的过程，教学中，教师可以数学实验为载体，推行探究性学习，拓展探究空间，为学生的发展创造機会和平台。在这个过程中，需要注意的是，一是要正确处理动手和动脑的关系。“人生两个宝，双手和大脑。”在数学实验中，教师要引导学生把动手操作和动脑思考进行有机结合，在操作中思考，在思考中操作。二是要正确处理教师主导和学生主体的关系。在数学实验中，教师要充分发挥学生的主体作用，引导学生自主思考与合作交流，教师只需注意把握学生思考的整体方向，避免学生在思考路径上出现偏差，做好学生学习的指路人。

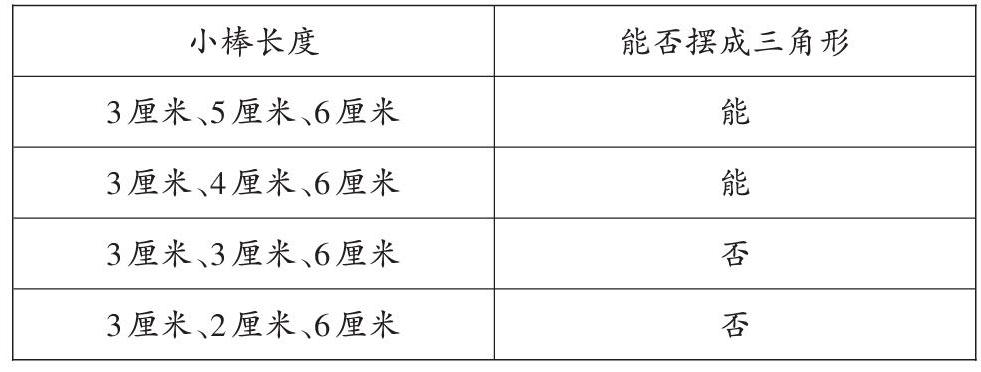
如，将四组小棒（3厘米、5厘米、6厘米，3厘米、4厘米、6厘米，3厘米、3厘米、6厘米，3厘米、2厘米、6厘米）分给学生进行摆三角形的实验。在实验中，教师发现有的小组用3厘米、2厘米、6厘米这组小棒也摆成了三角形，对此，教师引导学生进行观察和分析：3厘米、2厘米、6厘米是否真的可以摆成三角形？这时，有的学生发现，这组小棒摆成的三角形并不是“严丝合缝”的，而是有一定空缺的。学生很快得出结论：这组小棒围成的图形不是封闭图形，也就算不上三角形了。此外，教师引导学生进一步思考：为什么3厘米、3厘米、6厘米这组小棒也不能摆成三角形？学生通过操作和分析认为：当两根小棒的长度之和等于第三根小棒的长度时，较短的那两根小棒就会与最长的那根小棒“重合”，确实不能摆成三角形。最终，学生通过实验得出如下结论：

数学实验在抽象的数学知识和学生思维之间搭建了一座沟通的桥梁，有利于学生在“做数学”中有所发现、有所创造。在实验过程中，教师引导学生用三根小棒摆三角形，当三根小棒无法摆成三角形时，又引导学生进一步思考其中的原因，由此，在实验操作中融入了浓厚的思维元素。学生在经历了操作、思考和比较等活动后，不但得出了正确的实验结果，还培养了严谨求实、一丝不苟的数学精神。

三、在提问后思考，给予学生思考的时空

“问题是数学的心脏。”提问是数学教学中应用最普遍的教学方式之一。好的数学问题往往能够启动学生的思维引擎，点燃学生的思维火花，把学生的思考“润物无声”地引到知识本质，使学生的思维向更深处漫溯。需要注意的是，教师在提问之后要留给学生充分的思考、交流的时间和空间，暂缓揭示问题答案，使学生在自主思考与合作交流的基础上自主得出结论，并鼓励学生从不同的角度论证自己的结论，从而使学生的思维建立在理性的思考之上。

师：结合实验结果，请同学们思考，怎样的三根小棒才能摆出三角形呢？

生1：我通过实验发现，当两根小棒之和大于第三根小棒的时候，就能摆成三角形;当两根小棒之和小于或等于第三根小棒的时候，就不能摆成三角形。

生2：我不同意这个观点。比如3厘米、2厘米、6厘米这组小棒，尽管满足2+6>3，但是这三根小棒仍然不能摆成三角形，这又如何解释？

生3：我认为只要满足较短的两根小棒的长度之和大于长的那根小棒，就能摆成三角形。

生4：我认为只要满足任意两根小棒长度之和大于第三根小棒，就能摆成三角形。

生5：对，“任意”二字很重要，不能省略。

实验操作后，教师及时提出问题“怎样的三根小棒才能摆出三角形呢？”，在充分思考和交流的基础上，学生初步得出结论。然而，探究的过程必然是曲折的，就在大多数学生认为已经“大功告成”的时候，有学生举出了反例，教师再次给予学生充足的时间去思考。学生通过对“任意”二字的推敲和斟酌，在自我否定的过程中实现了对知识的精准认识，也使学生的思维变得更加严谨、清晰。

四、在应用中思考，实现思维品质的提升

在实验教学中，教师不能仅满足于学生通过操作和分析得出正确的实验结论，更为重要的是，要教给学生理性的思维方法，引导学生用数学思维来思考问题，把实验当中得到的结论灵活地运用到问题的解决当中，并在这个过程中实现思维品质的提升。

师：我这里有一根长度为10厘米的吸管，要把它剪成三段，用线穿成一个三角形。如果先剪第一刀，右边的这段是一条边，左边的这段将分成两条边。那么，右边的这段最长是多少厘米（整数）？

生1：4厘米。

师：为什么？

生1：因为只有这样才能保证剩下的两条边之和大于4厘米这条边。

运用知识是判断学生是否理解知识的“试金石”。教学中，教师设计問题，引导学生把实验结论运用到问题的解决当中，在问题的解决中营造“思维场”，让学生的思维灵动起来，让学生的认识更为深刻。

数学家波利亚曾指出：“数学既像一门系统的演绎科学，又像一门实验性的归纳科学。”实验教学法为学生提供了动手操作和动脑思考的平台，让学生亲身体验知识产生的过程，不但为学生深刻理解知识提供了可能，而且营造了思考的氛围，使课堂充满“探索味”，让学生的思维飞扬起来，真正实现学生数学思维的发展和提升。

（责编 罗 艳）