培问题之“壤” 长思维之“花”

施李丹 姚海燕

[摘 要]针对小学低段学生提问中的“问题思考不敏锐”“问题呈现不主动”“问题表述不清楚”等现状，主张实施“思·现·炼”策略，即根据小学低段学生的认知特点和思维特点，引导学生精准化思考问题，将问题紧扣数学本质;再鼓励学生主动地呈现问题，凸显困惑思路;最后提升学生的语言思维。以估测习题教学为例，谈如何利用“思·现·炼”策略培养学生发现和提出问题的能力，提升学生的思维水平。

[关键词]估测;习题教学;思维能力

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2021）29-0016-04

【课堂回顾】

教学片段1：给予参照物表象，首次思考估测问题

出示人教版教材二年级上册“长度单位”单元练习一的第1题：

1.引导学生思考“什么是估”

师：仔细读题，有不理解的地方吗？

生1：这个“估计”是什么意思？

师：哪位同学知道？

生2：我认为估计就是大概的意思。

生3：我感觉估计的话不用真的去测。

师：确实，估计长度就是大概多长的意思，如果只是要知道估计的数据，我们是不用进行测量的。既然理解了估计的意思，就请独立解决问题。

2.引导学生思考“怎么估才准”

（1）正误辨析，初构问题

师：在解决问题的过程中遇到什么问题吗？

（学生没有反馈）

出示（学生估计的答案）：2厘米、3厘米、4厘米、10厘米。

师：大家觉得哪个估得准？

生4：3厘米，因为我测量出来的也是3厘米。

师：这位同学没有测量就估出3厘米，确实厉害！其他同学会感到困惑吗？

生5：为什么估3厘米？而不是1厘米、2厘米……

师：你认为3厘米怎样？

生5：很准。

师：所以你想问的是？

生5：怎么估才能更准一些呢？

师：非常了不起的问题，你这个问题在解决估测问题上是非常重要的！接下来我们就一起探究怎么估。

（2）展露隐思，探寻估法

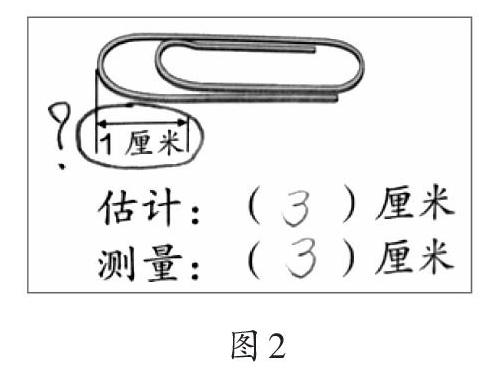
师：有位小朋友给“1厘米”标了“？”（如图2），现在就请她来说说感到疑惑的问题。

生6：这个是干什么的？

师：不要紧张，试着让大家都明白你要表达的意思。

生6：就是为什么要1厘米……

（教师再三鼓励，生6还是说不下去）

师：谁来帮他把问题说清楚、说完整？

生7：我觉得他是想问“为什么标1厘米，而不是标其他的长度？”。

生8：他想问1厘米是不是能帮助我们估计？

生9：1厘米在这里到底有什么用？

师：你们都很厉害，不仅能互帮互助，还能想出这么了不起的问题。大家记得在哪里接触过和“估”有关的题吗？

生10：上学期学过估数，几个十。

师（出示题目）：你的记性真好，还记得当时是怎么估的吗？

生11：先知道10颗有多少，然后看这一堆里大概有几个10颗就可以估作几十。

师：和我们今天这道题目有什么联系？

生12：一样的道理，1厘米和10颗都是用来帮助我们估计的，看回形针大概有几个1厘米就是几厘米。

師：确实，“10颗”“1厘米”就是起到参考的作用，是参照物。不管什么物体，只要找到参照物，观察这个物体有几个参照物的大小就能估得准，如果一开始估的方法不对的再来试一试吧！

教学片段2：抽离参照物表象，深度思考估测问题

出示数学课堂作业本第2页第2题：

1.聚焦冲突，再探估法

（1）自构表象1厘米：估测时未出示“1厘米”也可估

生1：这一题怎么估呀？

师：我们不是学过怎么估了吗？你的问题是什么？

生1：这一题没有1厘米了，怎么估？

生2：1厘米多长难道你不知道？

师：知道1厘米多长确实很重要，无论1厘米是否出示，心里都要有它。

（2）灵活拓宽参照物：估测参照物并非只有“1厘米”

生3：可是腰身呢？

师：慢慢来，把话说清楚、说完整，腰身怎么了？

生3：一拃长可以估计，因为看自己的手就能想象有几个1厘米，但腰的话就要加几十个1厘米，太麻烦了，怎么估？

师：这个问题确实是伤脑筋。怎么估才能不麻烦？

生4：参照物可以是一拃呀，我一拃是12厘米，量得5拃，估计是60厘米。

生5：把10厘米当作参照物也可以，用手大概量出10厘米后去围着腰身量一圈，看大概有几个10厘米就是几十厘米。

师：你们的方法都可行，而且你们都在述说一个道理：估测时为了方便可以寻找一个合适的参照物。

2.题后远思，再度提问

（1）对比生疑，联系生活

师：会估会测量了，那对于“估和测量”还有什么想问的？

生1：为什么又估又量？直接量不就好了？

生2：什么时候需要量，什么时候可以估？

师：都是好问题！那谁能举例说说什么时候需要量，什么时候可以估？

生3：如果我爸爸想戴我的手套，我就可以估计他戴不了，因为他的手太大了。

生4：如果我的手套坏了，妈妈想给我织新的手套就要量我手掌的大小。

师：同学们很擅于联系生活思考问题。确实，估和量在生活中有不同作用，能估计时用估更方便，但需要精确数值时就得量，避免出现差错。

（2）举一反三，延续思考

师：到现在为止，我们学了估数、估测，你还有什么想问或者想说的吗？

生5：除了估数、估测，还有什么也可以用“估”来解决？

生6：是不是还可以估大小？

师：你们已经会举一反三地思考问题了，真棒！今后我们还会学习和“估”有关的内容，所以留个悬念给大家，大家也可以自己去发现……

【课后反思】

教学片段1中，学生对于“估测”的学习属于首次，由于生活经验不丰富，学生对于“估”存在较多问题。教学片段2是学生学完估测后的课堂练习，虽然学生解决过“什么是估”和“怎么估”，但因为习题脱离了参照物，学生的思维再一次受阻，出现问题较多。低段学生对问题的感知不敏锐，问题呈现不主动，在提问时表达过于笼统或不清晰。因此，笔者在常态课上就会注重培养学生发现和提出问题的能力，通过引导学生精准思考问题、鼓励学生主动呈现问题、指导学生清晰表述问题来发展学生的思维能力。

一、逐引问思，提升学生的思维水平

教学时先引导学生思考问题从视点走入质点，最终带领学生思考发展的远点。所谓视点，即信息切入口;质点，即数学知识、方法上的核心点;远点，即质点之后可引领学生抵达的高度，即由数学知识延伸至生活或由一及类。

1.视点切入，基于文本理解的问题思考

在与文本对话中往往需要主动对接原有的生活经验和数学经验，而低段学生的感知能力较弱，理解词句的能力比较弱， 因此，促进低段学生思考问题可从文本信息切入，通过文本阅读自我诊断，从中发现问题。这同时也能考查学生是否带着思考在审题。

教学片段1中，笔者让学生阅读文本信息，生活经验不丰富、词汇量不足的学生的思维马上聚焦在了“估计”一词上，他们会提出问题“什么是估计？”。通过“估”的切入，学生理解了“估”的意思，才能继续思考更本质的内容，避免后续阶段的无效投入。

2.质点深入，基于本质探寻的问题思考

弗赖登塔尔曾说：“学习数学的唯一正确的方法是实行‘再创造，也就是由学生本人把要学的东西，自己去发现和创造出来。”为此，在知识的本质处、核心处要引导学生自己生发问题，引发学生深度思考，使学生的探寻能有效指向知识的本质。

理解“估”不是重点，“会估”才是本质。在教学片段1中，学生未意识到自己的问题时，笔者通过“正误辨析”“聚焦冲突”“对比生疑”“举一反三”等策略给予学生思考问题的方向，逐步引导学生思考核心问题“怎么估”。而在探究核心问题过程中，笔者引导学生提出一个个问题：“1厘米有什么用？”“没有1厘米了怎么估？”“腰身用1厘米不好估怎么办？”……以小问题的解决最终解决大问题。

3.远点延伸，基于外延联想的问题思考

数学学习既要知内涵，又要知外延。除了从知识的核心处去思考问题，还要让学生感受知识的价值。教师是学生思维生长的助推手，解决完问题并不代表学习结束。

教学片段2中，“会估会测量了，那对于‘估和测量还有什么想问的？”就是在学生理解了估意、估法后，笔者引导学生对比“估”和“测”。学生提出的问题“为什么又估又量？直接量不就好了？”“什么时候需要量，什么时候可以估？”虽然不作为学习要求，但笔者希望学生学数学的同时也会用数学，因此让学生思考并观察生活。此外，笔者引导学生通过举一反三来思考问题“还可以用估来解决什么？”“是不是还可以估大小？”……考虑到教学要为下一次学习留住生长点，笔者没有解说答案，因为问题不一定必须得解决，学生发现并提出問题的过程就能促进他们思维生长。

二、外显问意，满足学生的心理需求

低段学生正值喜欢提问的年纪，但教师在课堂上经常感受不到，原因有二：一方面，学生因害怕提错问题而不敢问;另一方面，一节课只有40分钟，教师不可能时时等待学生提出问题。因此，在“育问”路上教师要感同身受不同学生的处境，满足不同学生的心理需求，让学生养成主动提问的习惯。

1.静待花开，给予提问能力弱的学生思考问题的机会

学生认知发展水平的不同，导致他们感悟问题的时间也有所不同，提问能力弱的学生往往需要较长的时间才能感悟到自己的问题。数学教学应最大程度地开启每个学生的智慧潜能。当学生处于思考问题的环节，笔者均会留出一定的思考时间。对于提前发现问题的学生，笔者要求他们以“疑问手势”（如图6）示意，避免脱口而出的问题打断其他学生的思考，待较多学生发现问题后笔者再指名学生提问。

2.以退为进，呵护胆小学生思考问题的意识

在看似热闹的课堂之下，潜藏着很多“沉默的疑惑”，一些生性胆小的学生不擅长展示自己的内心活动，也就得不到教师点拨的机会。笔者不强求这些学生必须提问，而是鼓励他们在探究过程中思维受阻时可以圈圈画画，或标智慧符号“？”，笔者就能通过这些符号及时关注到他们的内心需求。

在教学片段1中，给“1厘米”标了“？”的学生的成绩不是很好，他性格也较为内向，基本不敢举手提问。“1厘米的作用”属于探究估测法的必经之路，聪明的学生也许根本不会想到这个问题，但对于学困生而言，发现这个问题时就表明思维在生长，因此，教师要给予他们关注和鼓励，让他们的问题意识得到充分呵护。

3.见缝插针，展露学生思维生长的节点

在整个课堂教学中教师要以学生为主体，致力于培养学生在学习过程中的自主性和参与性，提高学生的表现力。因此，笔者允许学生在任何时候发现数学问题，但没有提问机会时，可以高高举起“智慧”手势，避免学生的真问题由于没机会提问而流失。

教学片段2中一句“可是腰身呢？”属于学生真实存在且迫切想解决的问题，在课堂如常进行之时，“可是腰身呢？”这个问题再一次点燃了集体的思维火花，带给了提问者成功的体验。学生经历了“用1厘米为参照物来估→去掉1厘米后靠想象来估→非1厘米为参照物来估”的思维过程，这个过程将估测的方法展现得淋漓尽致。

三、培育问语，发展学生的语言思维

“能用语言组织表达出来，是对认知的一种证明。思维在没有被表达出来前是一团无形的东西，语言将思维表达出来后，思维就变成了有意义的信息。”低段学生的语言表达能力往往还不成熟，教师要有针对性地培养，使得学生在表达问题的过程中获得新的思考路径，促进语言思维的提高。

1.表达卡点时，及时点拨

提问开始阶段，学生的思维会呈现无序状态，学生表述时会词不达意，作为课堂中的引导者，教师应该帮助学生将无序思维变得有序，混乱的语言变得清晰。在教学片段1中，当学生提出问题“为什么估3厘米？而不是1厘米、2厘米……”时，他们的思维是模糊的，笔者通过“你認为3厘米怎样？”助力学生语言表达的突破，直至引导学生提出“怎么估才准？”。同样，在教学片段2中，教师通过“以问引问”使得学生能更清晰地表述问题“没有1厘米了怎么估？”。

学生表达问题的过程就是一个“试误”阶段，教师通过点拨使学生的问题语言由不精准向精准转变。这里要注意的是点拨需适量、及时，点到为止。

2.问语模糊时，引导生生共振

学生思考初期形成的问题是笼统、模糊的。学生发现头脑里有些想法，想表达自己的问题时，往往讲了半天，别人也不知道他想表达什么。此时，可以让其他学生补充和提示，使得问题逐渐清晰化。在此过程中，提示的学生得到了锻炼，提问的学生也能获得能力的提升。

教学片段1呈现了生生思维共振的画面，当学生提出“1厘米是干什么的？”这样模糊的问题时，笔者鼓励其他学生来帮助其完善问题。由于学生的思维基本处于同一个水平，他们更容易有共鸣及互相理解。完善者与分享者这场“思维的乒乓球比赛”，也能促使更多的学生参与到问题中。

3.思维放松时，鼓励自由提问

低段学生的问题意识需要被呵护，教师不要为了提问而让学生去提问。这样会让学生常常处于紧张状态，反而不利于学生提问能力的发展。教师要引导学生的提问由不自觉向自觉转变，提问不是目的，思考才是目的。

教学片段1中，有学生质疑“1厘米”的作用时，由于大家感觉自己是在帮助同学完善问题，因此心态较轻松，便开启了自由状态式提问：“为什么标1厘米，而不是标其他的长度？”“1厘米是不是能帮助我们估计？”“1厘米在这里到底有什么用？”。教学片段2中，在解决完怎么估的问题后，学生处于轻松状态，在笔者的引导下学生也开始“畅谈困惑”。思考问题就是一种思维的活动，教师不要贸然打断学生的自由提问，而是使学生能更久地处于思考的氛围中。

总之，学习是一个循序渐进的过程，“发现和提出问题”能力的培养亦是如此。无论新课教学还是习题课教学，教师均应耐心引导学生思问、现问、述问，从而提升学生的数学思维能力和语言表达能力。

【本文系海盐县2019年度教育科学规划微型课题《小学低段数学学生提问的“思·现·炼”策略研究》研究成果。】

（责编 童 夏）