基于核密度估计的拖拉机传动轴载荷外推方法
2021-11-05李淑艳翟友邦王小龙李若晨杨子涵宋正河
李淑艳 翟友邦 王小龙 李若晨 杨子涵 宋正河
(中国农业大学 工学院,北京 100083)
载荷谱是机械零部件寿命设计和可靠性分析的基础[1]。传动轴作为拖拉机传动系的主要组成部分,承担着从变速箱向驱动桥传递动力的功能,是影响拖拉机整机可靠性的关键零部件。编制传动轴载荷谱,可以提高疲劳试验的可信度,对提高传动系可靠性具有重要意义。出于成本考虑,载荷测试试验时间相对较短,需要对测试载荷进行外推获得全寿命载荷谱。
常用的外推方法有时域外推和雨流矩阵外推[2]。其中,时域外推能够保留载荷时间顺序,适用于平稳性载荷,当载荷表现出非平稳性时,其计算量较大。雨流矩阵外推虽不能保留载荷时间顺序,但其计算量小,对平稳和非平稳载荷均适用,具有较强工程应用价值。由于拖拉机作业环境复杂,导致传动轴承受非平稳性载荷,因此适合采用雨流矩阵外推的方法。
雨流矩阵外推常用的方法有参数法和非参数法。参数法通常采用正态分布拟合均值频次,威布尔分布拟合幅值频次。贾海波[3]基于单参数法对轮式装载机传动系载荷进行外推,在此基础上获得了均幅值二维载荷谱,并给出了疲劳试验一维程序谱加载方案。已有研究[4-5]通过参数法对轮式装载机半轴载荷进行外推,其中,翟新婷提出的混合分布的载荷谱编制方法对载荷多峰分布的拟合难题拓宽了解决思路,但拟合精度仍需提高。陈东升等[6]以军用车辆传动系统为研究对象,采用双参数雨流计数法,对载荷的幅值和均值进行计数,并将测试载荷外推得到全寿命历程二维设计载荷谱,建立了可用于疲劳寿命估算的八级程序载荷谱。采用基于参数法的雨流矩阵外推方法时,由于非平稳性载荷具有单峰和多峰的特点,存在拟合不通过或分布函数难以确定的局限。非参数法是基于核密度估计(Kernel density estimation,KDE)的思想对雨流矩阵进行外推,可以直接得出任意载荷的密度值,克服分布函数拟合的缺陷,为多峰复杂载荷的精确拟合提供了解决办法。李莺莺等[7]采用非参数估计方法对挖掘机液压泵载荷进行外推,得到全生命周期内每个载荷循环可能出现的频次,而且可以保证每个迟滞回环的结构不被破坏。张晓晨等[8]选择基于载荷扩展的非参数外推方法分别对液压挖掘机的4个作业段进行外推,获得全寿命下的长期载荷谱。李研[9]提出了基于全带宽非参数外推模型和载荷扩展的非参数雨流外推方法,针对轮式装载机,根据实测载荷数据进行了试验验证与载荷谱编制工作,并指出带宽对非参数外推精度的局限性。Johannesson.P等[10]将极值理论与非参数法结合起来,对汽车半轴载荷进行了外推处理。
虽然国内外都对非参数外推开展了相关研究,但外推精度依然亟待提高。针对上述问题,本研究拟以拖拉机传动轴为研究对象,搭建传动轴无线扭矩测试系统并进行载荷测试,分析测试载荷分布特征,运用拇指法(Rule-of-thumb,ROT)求带宽,提出一种改进的基于核密度估计的载荷外推方法对测试载荷进行外推,并从参数统计、拟合度和伪损伤3个方面对所提出的方法的精度和有效性进行验证。
1 拖拉机传动轴田间试验
试验样机为LX2204拖拉机,所搭载的犁耕机型号为MULTI-MASTER153T。在传动轴中心附近粘贴应变片,同时无线扭矩节点固定在传动轴上以确保传感器与传动轴的相对位置保持不变。选用北京必创科技有限公司生产的TQ201型无线扭矩采集器,其使用应变片为BF350-3BA型,基于TQ201搭建的拖拉机传动轴无线扭矩测试系统见图1。
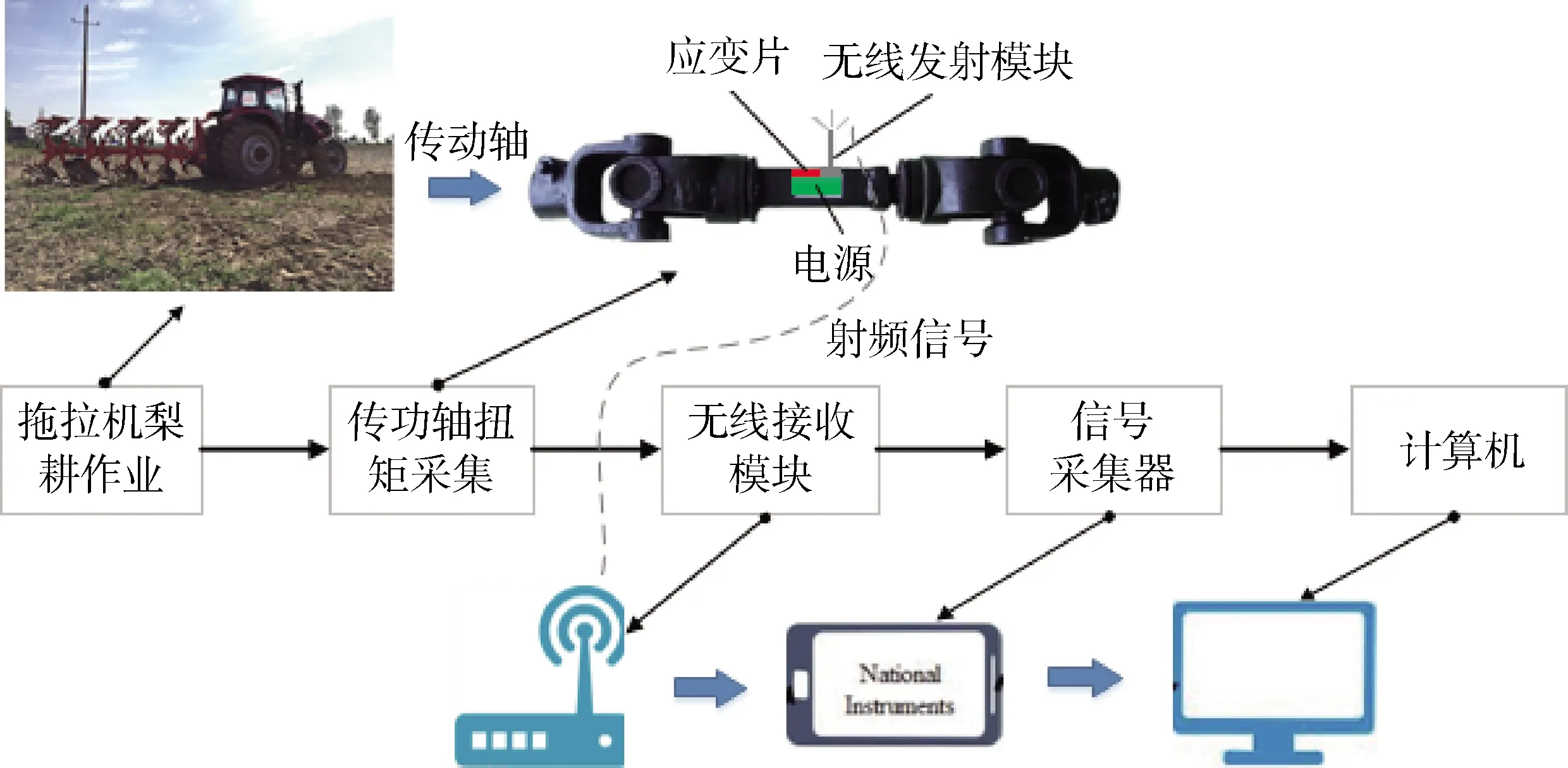
图1 拖拉机传动轴无线扭矩测试系统Fig.1 Tractor propeller shaft torque test system
田间试验地点为河南省洛阳市孟津县金村面积约13 hm2的砂土农田,玉米秸秆留茬高度约10 cm。采集了犁耕、旋耕、运输和联合耕整等工况的传动轴载荷试验数据,采样频率为100 Hz。为保证测试载荷能真实反映作业工况,根据GB/T 14225—2008《铧式犁》中的规定,试验过程由驾驶员按其习惯进行操作。试验中拖拉机的档位为中三档,行驶速度为5~10 km/h;耕深和作业宽幅分别为0.32和2.1 m;碎土率为99.2%。对田间作业环境进行测量,风速为4.6 m/s,环境湿度和温度分别为21%和25.6 ℃;距土壤表面5、10和15 cm处的含水率分别为6.28%、9.84%和12.2%。
2 基于核密度估计的载荷外推方法
本研究采用雨流矩阵外推中基于核密度估计理论的非参数法和按比例外推方法对测试载荷进行外推处理,并对非参数法在外推过程中带宽的选取进行探究,载荷的外推流程见图2。
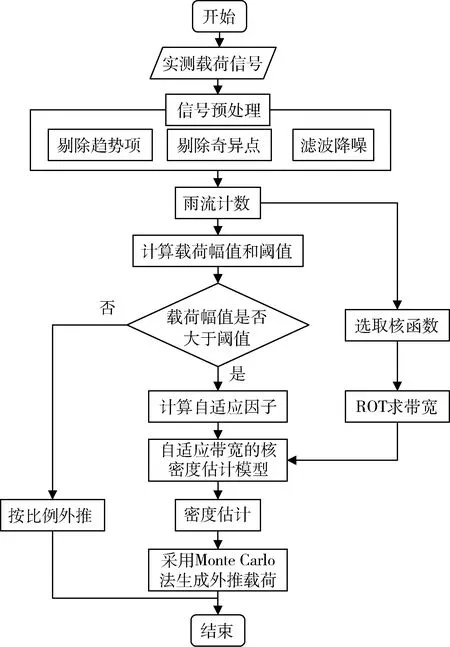
图2 基于核密度估计的载荷外推方法流程Fig.2 Process of load extrapolation method based on kernel density estimation
2.1 信号预处理
田间试验共获得8组犁耕工况传动轴载荷数据,受测试环境和测试系统等原因影响,田间测试信号中不可避免地会存在干扰噪声。通过多项式拟合去除测试信号中的趋势项、幅值门限法和动态标准差法去除信号中的奇异点以及巴特沃斯低通滤波器滤除高频载荷,由于高频载荷大部分是小载荷,因此低通滤波可以将对结构损伤贡献很小的小载荷滤除。图3为预处理后的部分犁耕工况传动轴测试载荷时间历程。

图3 犁耕工况传动轴扭矩时间历程Fig.3 Torque time history of propeller shaft in ploughing conditions
2.2 核密度估计
采用核密度估计理论对雨流矩阵进行外推属于非参数法。核密度估计能较准确估计任意分布载荷数据的密度值,当带宽选择恰当时,密度值能达到较高的精度,核密度估计的具体步骤为[11]:
1)采用雨流计数法将载荷-时间历程转换成雨流矩阵。
2)确定核函数K(x,y)和带宽h,构建核密度估计模型f(x,y)。
3)根据核密度估计模型和敏感系数计算自适应因子λi:
(1)
式中:α为敏感系数,经验值为0.5;n为样本量,xi、yi分别为雨流矩阵初值(From)和终值(To)。
4)根据自适应因子确定自适应带宽的核密度估计模型:
(2)
首先采用核密度估计模型对雨流矩阵进行密度估计获得密度矩阵,然后采用Monte Carlo法对密度矩阵进行随机数模拟,生成外推载荷。
2.3 带宽确定
从式(2)可以看出,核函数和带宽影响核密度估计精度。研究表明[12-13],核函数对核密度估计精度影响较小,带宽是影响核密度估计的主要因素。带宽过大,会导致载荷特性丢失;带宽过小,则会在密度中引入大量虚假波型,造成密度估计不稳定。本研究结合拖拉机传动轴载荷特征确定ROT带宽计算方法。
2.3.1R0T带宽计算方法
本研究选取高斯核函数作为核密度估计模型的核函数,并在核密度估计模型的基础上确定带宽计算方法。针对传动轴测试载荷,采用四点雨流计数法将测试载荷转换成初值(From)- 终值(To)雨流矩阵。雨流矩阵中存在单峰载荷和多峰载荷(图4)。ROT能根据单峰载荷和多峰载荷的特性,通过载荷样本的标准差和标准四分位距(Standardized interquartile range)确定出最优带宽[14-16]。
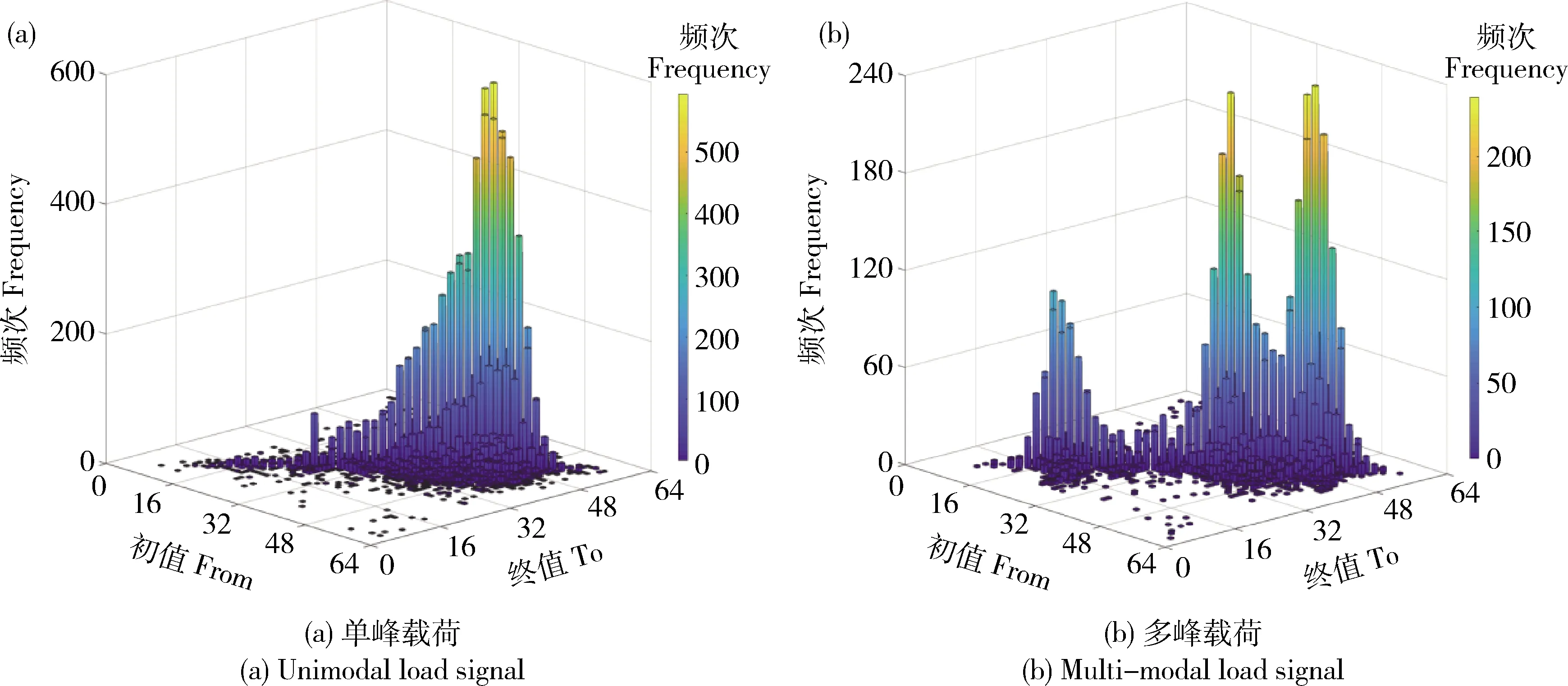
图4 测试载荷雨流矩阵分布特征Fig.4 Test load rain flow matrix distribution characteristics
基于高斯核函数的核密度估计模型的ROT求带宽h的公式为:
(3)
式中:A为高斯分布的最小值;σ为样本标准差;IQR为数据的标准四分位距。
拖拉机传动轴载荷具有大载荷较为分散,中小载荷相对集中的特点。对犁耕工况传动轴测试载荷雨流矩阵中的载荷进行简化(图5)。当用式(3)计算的带宽应用于a点的密度估计时,带宽会偏小。在以带宽为半径的圆内计算a点的概率密度分布,并进行Monte Carlo随机数模拟。如图6所示,由于带宽偏小,产生的随机数会过于集中。可以适当增大带宽以提高随机数的分散性,通过减小样本量来增大带宽。参照时域外推选取大载荷阈值的原则和实际外推效果,选择总样本量的80%计算带宽,则修正样本量N为:

a代表分散性较强的大载荷,b代表分布相对集中的中小载荷。Point a represents a large load with strong dispersion, point b represents a relatively concentrated medium and small load.图5 犁耕工况测试载荷雨流矩阵分布点Fig.5 Rain flow matrix distribution points of test load in plowing conditions
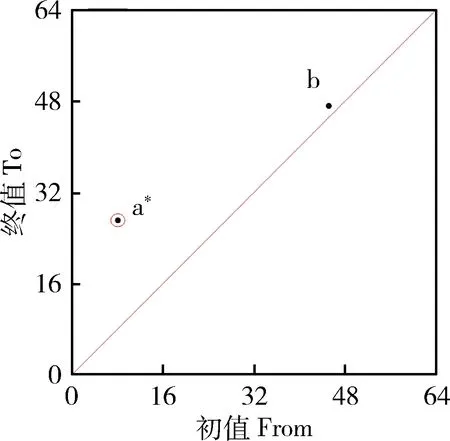
a*代表对a点的大载荷进行密度估计。a* represents the density estimation of the large load at point a.图6 大载荷核密度估计Fig.6 Rain flow matrix large load kernel density estimation
N=[0.8×n]+1
(4)
2.3.2核密度估计应用范围
应用式(1)计算出的载荷分布集中的区域,其自适应因子较小,即发生概率较大,针对这类载荷采用按比例外推法可以保留其原分布,且外推后仍在该区域,符合原载荷较集中的特征。同时采用线性外推后,在Monte Carlo模拟时略去此区域,计算速度可得到大幅提升。
对于雨流矩阵分散性较强(大载荷)的区域使用基于KDE的非参数法外推。在Monte Carlo模拟时会在其周围产生新的分布点(图7),新分布点符合原载荷分散性强的特性。

a’ 代表Monte Carlo模拟产生的新分布点。a’ represents the new distribution point generated by Monte Carlo simulation.图7 KDE外推结果Fig.7 The results of KDE extrapolation
样本量也是影响核密度估计精度的一个因素,为确保有较高的外推精度,需保证非参数法有足够多的样本量,因此需要在载荷的分散性和样本量之间寻求一个合适的阈值。根据拖拉机传动轴在各工况下的载荷分布特征及载荷对疲劳损伤的贡献度确定阈值。
1)计算雨流矩阵中载荷的幅值a:
(5)
式中:F为雨流矩阵的初值;T为雨流矩阵的终值。
2)定义非参数法和按比例外推法之间的阈值t:
t=[0.1max(a)]+1
(6)
通过上述分析和修正,用于拖拉机传动轴载荷外推的方法为:
(7)
式中:k为外推倍数;Ns为小载荷循环数;G(x,y)为采用基于KDE的非参数法的载荷外推函数。
3 载荷外推
以图3所示犁耕工况为例进行载荷外推计算。因测试载荷为扭矩,雨流计数是基于材料应力迟滞回线原理形成的,故将扭矩转换成应力进行计数处理,转换公式为:
(8)
式中:τ为应力,Pa;T为扭矩,N·m;Wt为抗扭截面系数,Wt=πd3/16,d为轴的直径,m。
将犁耕工况传动轴扭矩转换成应力(图8),提取测试应力数据的转折点并用四点雨流计数法得到雨流载荷循环的初值、终值及其频次信息,对载荷进行分级并编制成雨流矩阵。本研究将雨流载荷分成64级,编制成64×64雨流矩阵见图9。雨流矩阵的原始样本量n=1 488,根据式(4)计算出修正样本量N=1 191。根据式(5)和式(6)进一步计算出阈值t=8.2 MPa,结合式(3)可计算出最优带宽为2.709和2.691。非参数法的外推参数见表1。
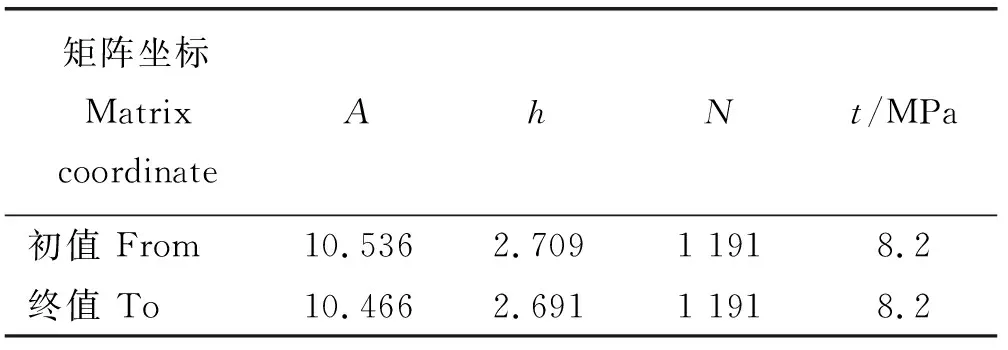
表1 基于核密度估计的非参数法外推参数Table 1 The extrapolation of parameters based on nonparametric method of KDE
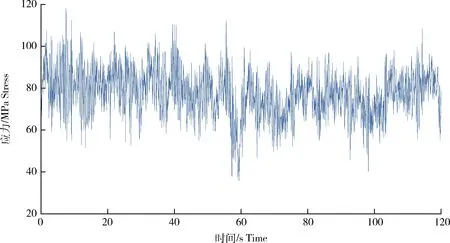
图8 梨耕工况传动轴应力时间历程Fig.8 Stress time history of propeller shaft in ploughing conditions

图9 基于应力数据编制的雨流矩阵Fig.9 Rainflow matrix based on stress data
根据阈值t划分非参数法外推载荷和按比例外推载荷。非参数法外推载荷见图10(a),样本数量为318,按比例外推载荷见图10(b),样本数量为1 170。

图10 犁耕工况传动轴载荷外推结果Fig.10 The result of different extrapolation methods of propeller shaft load in ploughing condition
取敏感系数α=0.2,采用上述核密度估计模型对雨流矩阵进行密度估计,并用Monte Carlo模拟产生与样本量相同的载荷。把非参数法外推的载荷和按比例外推的载荷合并形成一个雨流矩阵见图11,对比图9可以看出,外推1倍的雨流矩阵载荷分布与原始雨流矩阵载荷分布具有较高的相似度,保留了原有载荷的分布特征。相比于整段载荷使用核密度估计的传统非参数法,外推的运算速度得到大幅提高,当外推至全寿命频次(106)时,运算时间从0.502 310 s缩短至0.230 247 s,速度提高了54.16%。
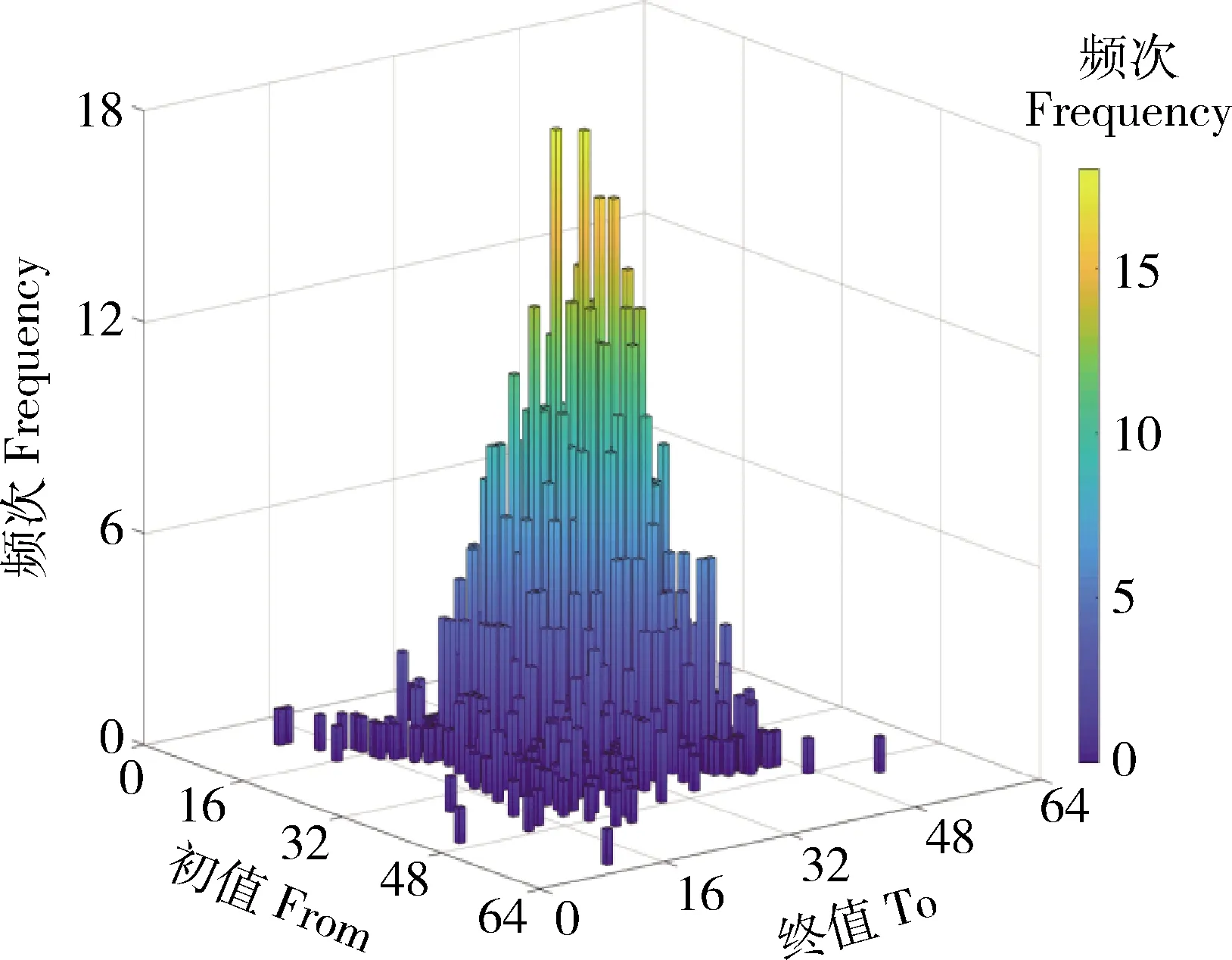
图11 犁耕工况传动轴总体外推结果Fig.11 Total result of extrapolation of propeller shaft in ploughing condition
4 外推结果验证
当外推方法选择合理时,外推载荷与测试载荷应具有相同的特征,本研究分别从统计参数、拟合度和伪损伤 3 个方面检验外推载荷的有效性。
4.1 统计参数检验
选取统计参数均值、标准差和最大值作为传动轴测试载荷与外推载荷的评判依据。对犁耕工况,采用本研究提出的基于核密度估计的载荷外推方法得到的外推载荷,其均值、标准差和最大值与测试载荷的误差分别为2.2%、0.87%和6.3%,均在工程应用允许误差范围内。旋耕工况、运输工况和联合耕整工况的均值、标准差和最大值误差这3种统计参数均小于10%。综上表明外推载荷能较好地保留测试载荷的统计特性。各工况测试载荷与外推载荷的统计参数见表2。
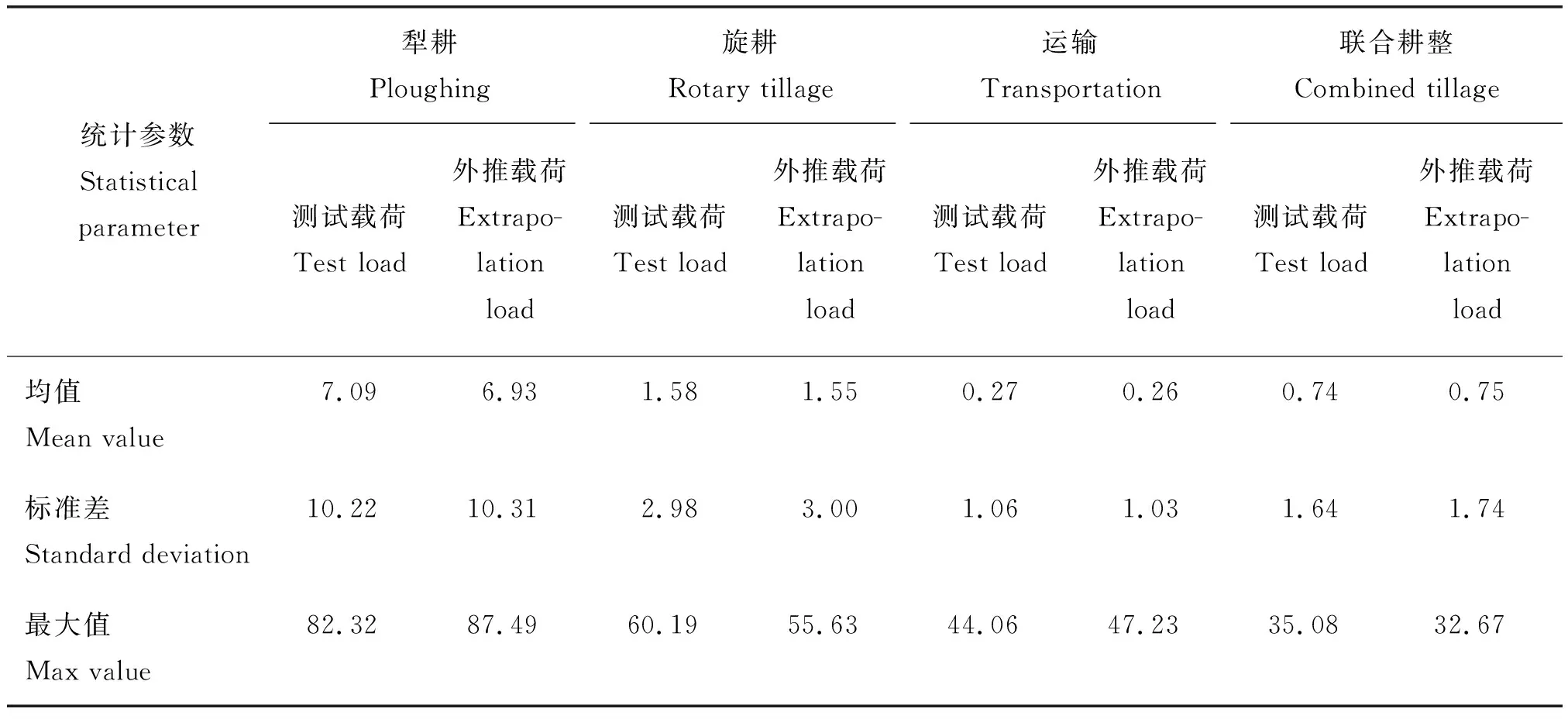
表2 不同工况下传动轴载荷统计参数Table 2 Statistical parameters of propeller shaft load under different working conditions MPa
4.2 拟合度检验
采用拟合度校验外推结果。载荷的循环次数和幅值是疲劳损伤的主要来源,通过绘制幅值累计频次曲线可以反映载荷的幅值和循环次数的统计结果。由外推载荷和测试载荷绘制成的雨流载荷幅值累计频次对比曲线见图12。
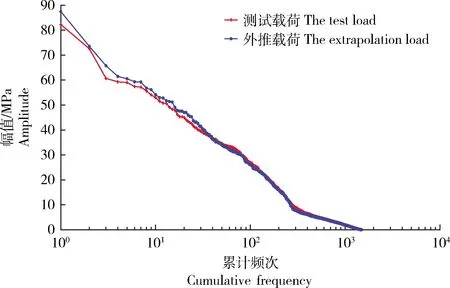
图12 犁耕工况幅值累计频次曲线Fig.12 Accumulated frequency curve of amplitude of ploughing condition
为判断外推载荷与测试载荷之间的差异,对曲线拟合度进行量化,用决定系数R2(Coefficient of determination)计算曲线之间的拟合度。对犁耕工况,外推载荷幅值的R2达到0.998,其中前100个大幅值载荷的R2为0.978,表明该方法保留了拖拉机传动轴载荷的分布特性。采用旋耕工况、运输工况和联合耕整工况下传动轴测试载荷进一步验证本研究所提外推方法的合理性,并与传统非参数法进行对比,结果表明该外推方法对传动轴不同工况载荷具有较高的适应性,外推的整段载荷和前100个大幅值载荷的R2均大于0.9,与测试载荷高度拟合。与传统非参数法相比,由本研究所提外推方法得到的R2均有较大幅度的提高,外推效果明显优于传统非参数法。决定系数R2见表3。

表3 不同工况下外推载荷的决定系数Table 3 Determination coefficient R2 of extrapolated load under different working conditions
4.3 伪损伤检验
外推载荷的最终目的是编制疲劳试验加载谱。在机械工程领域,分析复杂的交变载荷时,常通过计数法和损伤累积来计算疲劳。采用S-N曲线疲劳寿命模型计算构件的疲劳寿命,循环寿命与恒幅值应力的关系[17]为:
(9)
式中:α为材料属性参数;β为损伤指数;Si为恒幅值应力;Ni为循环寿命。
工程上常用Palmgren-Miner线性损伤理论计算伪损伤,该理论是基于S-N曲线各应力循环次数对材料造成伪损伤的线性累积结果[18],表达式为:
(10)
式中:Di为总伪损伤;ni为材料在Si载荷作用下的循环次数;Ni为载荷Si作用下的疲劳寿命循环次数。
为便于对伪损伤进行比较,定义伪损伤比为外推载荷对材料造成的伪损伤与测试载荷对材料造成的伪损伤的比值。伪损伤比越接近1,外推载荷与测试载荷的相似度越高。基于Palmgren-Miner线性损伤疲劳累积理论在Ncode软件中搭建伪损伤计算模型。
由本研究所提外推方法得到的犁耕工况外推载荷,其伪损伤比为0.999,与测试载荷具有高度一致性。同时计算旋耕工况、运输工况和联合耕整工况传动轴载荷的伪损伤比,其数值分别为0.992、0.998 和0.996,均能较完整地保留测试载荷的损伤量。
5 结 论
本研究根据拖拉机传动轴载荷特征,在采用ROT求得带宽的基础上,提出了一种基于核密度估计的载荷外推方法,并从统计参数、外推拟合度和伪损伤3个方面验证了方法的有效性。主要结论如下:
1)与传统非参数法相比,当载荷外推至全寿命频次(106)时,采用本研究所提外推方法可将计算时间缩短54.16%,当测试载荷量较多时,能够有效缩短外推时间,提高计算效率。
2)将犁耕工况的外推载荷与测试载荷进行对比分析。统计参数检验表明,均值、标准差和最大值的误差分别为2.2%、0.87%和6.3%,外推载荷很好地保留了测试载荷的统计特征;拟合度检验表明,前100个大幅值载荷的R2为0.978,整段载荷R2达0.998,外推载荷很好地保留了测试载荷的分布特征;伪损伤检验表明,伪损伤比达到0.99,外推载荷很好地保留了测试载荷的损伤量。
3)用本研究所提外推方法对旋耕工况、运输工况和联合耕整工况传动轴载荷进行外推,统计参数误差均小于10%,R2均大于0.9,伪损伤比均大于0.99,所提方法适用于拖拉机传动轴不同工况载荷外推。