拓扑旋转群上的同构定理*

梁倩倩，张 静

(闽南师范大学 数学与统计学院,福建 漳州 363000)

1 引言

旋转群的概念最初由A.A.Ungar[1]在研究爱因斯坦相对可接受速度的c球时提出.值得注意的是旋转群的结构出现在众多领域中，如数学、物理、非欧几里得几何学、群论、loop理论、抽象代数及分析学等.2015年，T.Suksumran和K.Wiboonton[2]探究了旋转群的一些基本性质，引入了L-旋转子群，并证明了旋转群上的三个同构定理.L-旋转子群及正规旋转子群的提出为旋转群陪集空间的研究奠定了基础.2017年，W.Atiponrat[3]赋予了旋转群拓扑结构使其二元运算在此拓扑下联合连续以及逆运算连续，从而给出了拓扑旋转群(topological gyrogroup)的概念，进一步W.Atiponrat证明了尽管具有更弱的代数结构，但拓扑旋转群仍具有一些与拓扑群相同的性质.2019年，蔡长勇、林寿、贺伟三位学者证明了每一个拓扑旋转群都是rectifiable空间，从而得出了拓扑旋转群的第一可数性与可度量性等价的结论[4].rectifiable空间作为拓扑群的推广，近年来受到广大国内外学者的关注.尽管rectifiable空间的研究已取得了一系列重要的成果，但美中不足的是只知道7维球面S7是rectifiable空间而不是拓扑群[5]，拓扑旋转群的出现为rectifiable空间的研究增添了实例.鲍猛和林福财[6]引入了强拓扑旋转群的概念，给出不是拓扑群的强拓扑旋转群(见[6]，例3.1])的实例，并证明每一个feathered强拓扑旋转群是仿紧的.

拓扑空间的商空间性质一直是拓扑学家们感兴趣的问题，如强拓扑旋转群的商空间性质(见[7]).本文主要探讨拓扑旋转群上的同构定理.本文所讨论空间满足T2分离性，未定义的符号及术语见[1，2，3,6].

下面我们回顾若干本文需要用到的定义与结论.

定义1.1[3]设⊕:G×G→G是非空集合G上的二元运算，则称(G,⊕)为广群.函数f:(G1,⊕1)→(G2,⊕2)称为广群同态，如果对任意a,b∈G1，有f(a⊕1b)=f(a)⊕2f(b).此外，从广群(G,⊕)到自身的双射广群同态称为广群自同构.广群(G,⊕)的所有自同构组成的集合用Aut(G,⊕)表示.

定义1.2[1]设(G,⊕)是广群.(G,⊕)称为旋转群，如果它的二元运算满足条件:

(G1)任取a∈G，存在唯一的单位元0∈G使得0⊕a=a=a⊕0.

(G2)任取a∈G，存在唯一的逆元⊖a∈G使得⊖a⊕a=0=a⊕(⊖a).

(G3)任取a,b∈G，存在gyr[a,b]∈Aut(G,⊕)使得对任意d∈G都有a⊕(b⊕d)=(a⊕b)⊕gyr[a,b](d).

(G4)任取a,b∈G，有gyr[a⊕b,b]=gyr[a,b].

定义1.3[2]设(G,⊕)是旋转群，H是G的非空子集，则H是G的旋转子群当且仅当下列条件成立：

(1)对任意a∈H，有⊖a∈H.

(2)对任意a,b∈H，有a⊕b∈H.

定义1.4[2]设(G,⊕)是旋转群，G的旋转子群H称为L-旋转子群，记为H≤LG，如果对任意a∈G,h∈H，都有gyr[a,h](H)=H.

定义1.5[3](G,τ,⊕)称为拓扑旋转群，如果下列条件成立：

(1)(G,τ)是拓扑空间.

(2)(G,⊕)是旋转群.

(3)二元运算⊕:G×G→G联合连续，其中G×G赋予乘积拓扑.

(4)逆运算⊖(·):G→G,i.e.，a→⊖a，是连续的.

显然若对任意a,b∈G，取的gyr[a,b]是拓扑群G上的恒等映射，则G是拓扑旋转群.

定义1.6[6]设(G,τ,⊕)是拓扑旋转群，则我们称(G,τ,⊕)是强拓扑旋转群，如果存在单位元0的一族邻域基U使得对任意U∈U和任意的a,b∈G，都有gyr[a,b](U)=U.

引理1.7[3]每一个拓扑旋转群(G,τ,⊕)都是齐性空间.

引理1.8[2]设φ:G→H是旋转群同态，则

(1)φ(0)=0;

(2)对任意a∈G，有φ(⊖a)=⊖φ(a);

(3)对任意a,b,c∈G，有φ(gyr[a,b]c)=gyr[φ(a),φ(b)]φ(c);

(4)对任意a,b∈G，有φ(a(⊖b))=φ(a)(⊖φ(b)).

2 主要结果

设G,H是旋转群.若映射φ:G→H定义为对任意a,b∈G，φ(a⊕b)=φ(a)⊕φ(b)，则称φ为旋转群同态.双射群同态被称为旋转群同构.如果存在一个从G到H的旋转群同构映射，则称G和H是同构旋转群，用G≅H表示.

同态φ的核kerφ是H中的旋转子群{0}在φ下的原象，因此kerφ也是旋转子群.kerφ在G的旋转自同构下是不变的，即对任意a,b∈G，有gyr[a,b](kerφ)⊆kerφ[2].旋转群G的旋转子群H称为正规的，如果它是G上某一旋转群同态的核.

若拓扑旋转群(G,τ,⊕)和(H,τ,⊕)间存在既是旋转群同构又是拓扑同胚的映射，则称(G,τ,⊕)与(H,τ,⊕)拓扑同构.

命题2.1 设G,H和K是旋转群.如果φ∶G→H,ψ∶G→K是使得ψ(G)=K且kerψ⊂kerφ的同态，则存在同态f:K→H使得φ=f∘ψ.此外，假设G,H和K是拓扑旋转群，映射φ和ψ连续.如果对H中单位元0H的任意邻域U，存在K中单位元0K的邻域V使得ψ-1(V)⊂φ-1(U)，则f连续.

证明对∀x∈K，取a∈ψ-1(x)，令f(x)=φ(a)，下面先验证f是良好定义的.首先若a,b∈ψ-1(x)，则ψ(a)=ψ(b)=x，从而⊖ψ(a)⊕ψ(b)=0K.由ψ是同态映射知ψ(⊖a)=⊖ψ(a),所以⊖a⊕b∈kerψ.因为kerψ⊂kerφ,所以φ(a)=φ(b).因此f是K到H上的映射且φ=f∘ψ.

对∀x1,x2∈K，取a1∈ψ-1(x1),a2∈ψ-1(x2)，则由φ是同态映射知a1⊕a2∈ψ-1(x1⊕x2)，因此f(x1⊕x2)=φ(a1⊕a2)=φ(a1)⊕φ(a2)=f(x1)⊕f(x2).即f是同态.下证f的连续性.

设U是H中单位元0H的任意邻域.由题设有，存在K中单位元0K的邻域V，使得W=ψ-1(V)⊂φ-1(U).由于φ=f∘ψ，故有f(V)=φ(W)⊂U，从而f在K中单位元0K处连续.根据旋转群是齐性空间知f连续.

推论2.2 设G,H和K是拓扑旋转群，φ∶G→H和ψ∶G→K是连续同态，使得ψ(G)=K且kerψ⊂kerφ.如果同态ψ是开的，则存在连续同态f∶K→H使得φ=f∘ψ.

证明由命题2.1，存在同态f∶K→H使得φ=f∘ψ.往证f连续.设V是H中的任意开集，则f-1(V)=ψ(φ-1(V)).由于φ连续且ψ是开映射，故f-1(V)是K中的开集.因此f连续.

引理2.3[2]如果H是旋转群G的L-旋转子群，则集合{a⊕H∶a∈G}是G中不相交的划分.

根据[6，定理 3.7]，赋予G/H由映射π∶G→G/H诱导的商拓扑，其中π(a)=a⊕H,a∈G.显然映射π是开映射.

命题2.4 设(G,τ,⊕)是拓扑旋转群，H是G的L-旋转子群，则集族{π(a⊕U)∶0∈U∈τ}是商空间G/H在点a⊕H∈G/H处的邻域基.

证明事实上，显然π-1(π(a⊕U))=(a⊕U)⊕H.因为(a⊕U)⊕H是开集且π是商映射，所以π(a⊕U)是G/H中的开集.设W是G/H中a⊕H的任意开邻域，置O=π-1(W),则O是G中a的开邻域.从而存在G中单位元0的开邻域U使得a⊕U⊂O.因此，π(a⊕U)⊂W.

对于旋转群同态φ∶G→H，T.Suksumran和K.Wiboonton[2]通过下面的方式定义了集合G/kerφ上的二元运算：

(a⊕kerφ)⊕(b⊕kerφ)=(a⊕b)⊕kerφ，a,b∈G.

引理2.5[2]设φ∶G→H是旋转群同态，则赋予上述二元运算的G/kerφ是一个旋转群.

引理2.6[8]设(G,τ,⊕)是拓扑旋转群，H是G的正规旋转子群，则(G/H,τG/H,⊕)是拓扑旋转群.

引理2.7[2]若φ∶G→H是旋转群同态，则旋转群G/kerφ≅φ(G).

定理2.8 设G,H是拓扑旋转群，φ是从G到H的连续开满同态.对任意a∈G，令Φ(a⊕kerφ)=φ(a),则映射Φ∶G/kerφ→H是拓扑同构.

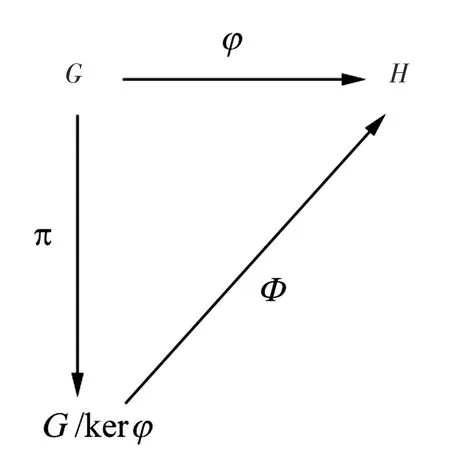
图1 拓扑同构Φ

图2 G/G0与H/H0拓扑同构

证明置N=kerφ.由于φ是从G到H的满同态，所以φ(G)=H.从而根据引理2.7知Φ是同构.

设映射π∶G→G/N是商同态，则根据Φ的定义知，φ=Φ∘π.因为Φ-1(W)=π(φ-1(W))，映射φ连续且映射π是开映射，所以对H中的开集W，有Φ-1(W)是开的.故Φ是连续的.设U是G/N中的开集，则有Φ(U)=φ(π-1(U))是H中的开集.从而同态Φ是开映射.于是，Φ是开连续同构，因此是拓扑同构.

引理2.9[2]设φ∶G→H是旋转群同态.如果K是G的旋转子群，则φ(K)是H的旋转子群.如果K是G的L-旋转子群且φ是满射，则φ(K)是H的L-旋转子群.

命题2.10 设G,H是拓扑旋转群，φ是从G到H的拓扑同构.如果G0是G的闭正规旋转子群且H0=φ(G0)，则商旋转群G/G0和H/H0是拓扑同构.对应的同构Φ∶G/G0→H/H0定义为对任意a∈G,Φ(a⊕G0)=b⊕H0，其中b=φ(a).

证明设映射πG0∶G→G/G0是商同态.由引理2.9知H0是G的L-旋转子群，且H0是旋转群同态πG0∘φ-1的核，从而H0是H的正规旋转子群.显然Φ是G/G0到H/H0的满同态.如果Φ(a⊕G0)=Φ(b⊕G0)，那么φ(a)⊕H0=φ(b)⊕H0.从而⊖φ(a)⊕φ(b)=φ(⊖a⊕b)∈H0.于是⊖a⊕b∈G0，即a⊕G0=b⊕G0.设πH0∶H→H/H0是商同态.注意到πH0∘φ=Φ∘πG0，且映射φ,πG0和πH0是连续的开同态，所以Φ也是连续的开映射.因此，Φ是拓扑同构.

引理2.11[2]设φ∶G→H是旋转群同态.如果K是H的旋转子群，则φ-1(K)是G的旋转子群.如果K是H的L-旋转子群，则φ-1(K)是G的L-旋转子群.

命题2.12[2]设φ∶G→H是旋转群同态，则对任意a∈G，下列条件等价：

(1)a～kerφb.

(2)⊖a⊕b∈kerφ.

(3)φ(a)=φ(b).

(4)a⊕kerφ=b⊕kerφ.

定理2.13 设G,H是拓扑旋转群，满射φ∶G→H是连续的开同态.如果H0是H的闭正规旋转子群，G0=φ-1(H0)，则G0/kerφ是G/kerφ的正规旋转子群且拓扑旋转群G/G0,H/H0和(G/kerφ)/(G0/kerφ)是拓扑同构.

图3 G0/kerφ,G/kerφ间的关系和G/G0,H/H0,(G/kerφ)/(G0/kerφ)间的关系分析

证明由假设H0是H的闭正规旋转子群，可设πH0∶H→H/H0是商同态.由于G0=φ-1(H0)，所以ker(πH0∘φ)=(πH0∘φ)-1(0H⊕H0)=

φ-1(πH0-1(0H⊕H0))=φ-1(H0)=G0，从而G0是G的正规旋转子群.所以存在商同态πG0∶G→G/G0.下证G0/kerφ是G/kerφ的旋转子群.

显然G0/kerφ⊂G/kerφ.从而显然对任意a,b∈G0，有⊖(a⊕kerφ)=⊖a⊕kerφ∈G0/kerφ且(a⊕kerφ)⊕(b⊕kerφ)=(a⊕b)⊕kerφ∈G0⊕kerφ.故由定义1.3知G0/kerφ是G/kerφ的旋转子群.

映射Φ∶G/kerφ→H/H0定义为Φ(a⊕kerφ)=φ(a)⊕H0，其中a∈G.由命题2.12知Φ存在且根据φ是同态及商旋转群G/kerφ和H/H0中二元运算的定义可得Φ是旋转群同态.从而由G0/kerφ=kerΦ知G0/kerφ是G/kerφ的正规旋转子群.

因为π和φ都是连续的开映射，所以πH0∘φ是G到H/H0的连续开同态且G0=ker(π∘φ).因此，商旋转群G/G0拓扑同构于H/H0.注意到对任意a∈G，ψ(a⊕kerφ)=φ(a)定义的映射ψ∶G/kerφ→H是一个拓扑同构.所以显然ψ(G0/kerφ)=H0.从而根据命题2.10有(G/kerφ)/(G0/kerφ)拓扑同构于H/H0.

定理2.14 设G是拓扑旋转群，H是G的闭正规旋转子群，M是G的任意旋转子群，则商拓扑旋转群(M⊕H)/H拓扑同构于拓扑旋转群G/H的旋转子群π(M)，其中映射π∶G→G/H是自然商同态.

证明显然，(M⊕H)=π-1(π(M)).因为M是G的旋转子群且π是G到G/H的满同态，所以由引理2.9及引理2.11知π(M),M⊕H分别是旋转群G/H,G的旋转子群.设Ø是π在M⊕H上的限制映射，即Ø=π|M⊕H:M⊕H→π(M).由于Ø-1(Ø(0G))=π-1(π(0G))=H，故有kerØ=H.从而根据定理 2.8知拓扑旋转群(M⊕H)/H和π(M)拓扑同构.

引理2.15[9]设(G,⊕)是旋转群且X是任意集合，f∶X→G是双射,则对任意a,b∈X，赋予二元运算a⊕Xb=f-1(f(a)⊕f(b))的X是旋转群.

定理2.16 设(G,τ,⊕)是拓扑旋转群，且设X是任意集合，f∶X→G是双射，则对任意a,b∈X以及U∈τ，赋予二元运算a⊕Xb=f-1(f(a)⊕f(b))以及诱导拓扑τ'={f-1(U)∶U∈τ}的X是拓扑旋转群.

证明根据引理2.15可得X是旋转群.事实上，对任意a,b∈X以及a⊕Xb在空间X中的任意开邻域f-1(W)有f(a)⊕f(b)=f(a⊕Xb)∈W，其中W∈τ.因为(G,τ,⊕)是拓扑旋转群，所以存在U∈τ,V∈τ使得f(a)∈U,f(b)∈V且U⊕V⊂W.于是，a∈f-1(U),b∈f-1(V)且a⊕Xb=f-1(f(a)⊕f(b))∈f-1(U⊕V)⊂f-1(W).故⊕X∶(X,τ',⊕X)×(X,τ',⊕X)→(X,τ',⊕X)在点(a,b)∈X×X连续.

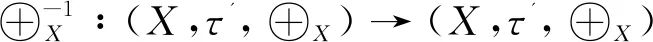
引理2.17[2]设(G,⊕)是旋转群，且X⊆G，则下列条件等价：

(1)对任意a,b∈G，gyr[a,b](X)⊆X.

(2)对任意a,b∈G，gyr[a,b](X)=X.

定理2.18 设(G,τ,⊕)是在单位元0G处具有对称邻域基U的强拓扑旋转群，且设f∶X→G是双射，则对任意a,b∈X以及U∈τ，赋予二元运算a⊕Xb=f-1(f(a)⊕f(b))以及诱导拓扑τ'={f-1(U):U∈τ}的X是强拓扑旋转群.

证明只需验证集族f-1(U)={f-1(U)∶U∈U}满足对任意a,b∈X以及每个U∈U，有gyr[a,b](f-1(U))=f-1(U).由于a⊕Xb=f-1(f(a)⊕f(b))，所以f(a⊕Xb)=f(a)⊕f(b).从而由引理2.15知f是旋转群同态.由题设(G,τ,⊕)是在单位元0G处具有对称邻域基U的强拓扑旋转群知，对每个c∈f-1(U)，根据引理1.8有f(gyr[a,b](c))=gyr[f(a),f(b)](f(c))∈U.从而对每个c∈f-1(U)，gyr[a,b](c)∈f-1(U)，说明gyr[a,b](f-1(U))⊂f-1(U).由引理2.17知(X,τ',⊕X)是强拓扑旋转群.