两参数布朗运动增量的一个泛函对数律
2022-10-26张晴晴刘永宏
张晴晴, 刘永宏
(桂林电子科技大学 数学与计算科学学院,广西 桂林 541004)
布朗运动也可称为维纳过程,作为具有连续时间参数和连续状态空间的一个随机过程,是随机过程学科中最简单、最基本、最常见的随机过程之一[1]。随着科学技术的进步,人们越来越意识到现实生活中影响某种随机现象的因素不是单一的,如天气变化,除了纬度位置,还与大气环流、海陆分布等因素相关。这促使学者寻找某种途径,把单参数情形所得到的结论推广到更为复杂的多参数情形。在多参数布朗运动中,两参数布朗运动最具代表性[2]。
布朗运动与两参数布朗运动的重对数律[3]问题研究最为广泛。毕秋香等[4]证明了在一定的假设条件下,广义布朗运动服从重对数律,得到并证明了相应的结果;文献[5-8]利用布朗运动在Hölder范数下的大偏差,得到了布朗运动增量在Hölder范数下的局部Strassen重对数律。文献[9-10]通过建立两参数布朗运动增量的大偏差结果,得到了在矩形集上两参数布朗运动大增量和小增量的Csörgö-Révész型增量Strassen重对数律;许杰等[11]利用两参数布朗运动增量的大偏差,得到了一类两参数布朗运动过程的连续模的情形。
鉴于此,针对两参数布朗运动对数律问题,给出了两参数布朗运动增量的大偏差,得到了两参数布朗运动的泛函对数律,并进行了证明。
1 预备知识

C0={f∈C;f(0,t)=f(s,0)=0},

设函数I:C0→[0,∞],定义如下:
设au:(0,∞)→(0,∞)为非减连续函数,满足:
1)au≤u,对任何u∈(0,∞);
2)u/au非减;
定义
Δ(s,t,aux,auy)=w(s+aux,t+auy)-
w(s+aux,t)-w(s,t+auy)+w(s,t),
0≤s≤u-au,0≤t≤u-au,(x,y)∈[0,1]2。
设
K={f∈H;2I(f)≤1}。
定义
Zs,t,u(x,y)=γuΔ(s,t,aux,auy)。
2 主要结果
定理1若1)~3)成立,则有
(1)
且对任意的f∈K,
(2)
3 若干引理
引理1[10]对任何闭集F⊂C0,
对任何开集G⊂C0,
引理2[10]对任何0 引理3设f∈H,定义 f*(·,·)=f(λ·,λ′·), 其中λ,λ′<1,则 ‖f-f*‖≤{((1-λ)(1-λ′))1/2+(1-λ)1/2+ (1-λ′)1/2}‖f‖H。 ‖f(·,·)-f*(·,·)‖= {((1-λ)(1-λ′))1/2+ (1-λ)1/2+(1-λ′)1/2}‖f‖H。 引理4[12](博雷尔-坎特利引理) 若 则 证明 引理5[13]设{ξn}n≥1为随机变量序列,若 则存在子列{ξnk},使得 因此 引理6若1) ~3)条件成立,则存在un→∞,使得 (3) 证明设A={g:‖g-K‖≥ε},则A为闭集,存在任意小的δ>0,使得 由引理2,有 故有 由引理5,可得 故引理6得证,从而式(1)得证。 引理7若1) ~3)条件成立,则对任意f∈K,存在子列{un=θn,θ>1,n≥1},使得 (5) 证明设si=iaun,tj=jaun,i,j=0,1,…, 若n足够大,则有 (6) 若n足够大,则由大偏差可得 因此, (7) 若n足够大,则由式3)有 故有 exp(-4log logun), (8) 由Borel-Cantelli引理可得: 引理8若1) ~3)条件成立,则对任何f∈K,有 (9) 证明设un如引理7中定义,对u∈(un-1,un], 有 (10) 则有 可得 (11) (12) 令θ→1,由式(10)~(12)和引理7,可得式(9),从而式(2)得证。 对布朗运动增量的重对数律有关问题进行了研究,将两参数布朗运动问题和单参数布朗运动问题进行对比,发现可以将单参数布朗运动增量的对律推广到两参数布朗运动增量的情形。通过对两参数布朗运动增量在一致范数下的对数律的探讨,今后还可以进一步探究两参数布朗运动增量在Hölder范数下的对数律以及两参数布朗运动增量的钟型重对数律。
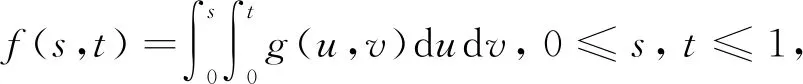
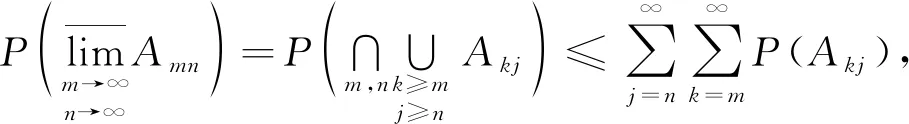
4 定理1的证明
4.1 式(1)的证明

4.2 式(2)的证明
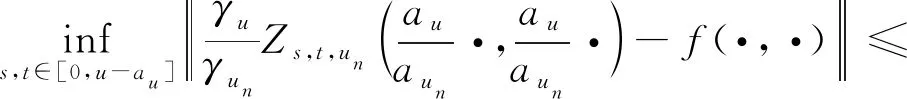
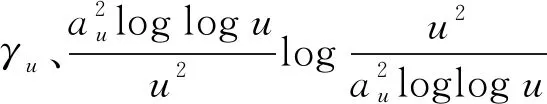
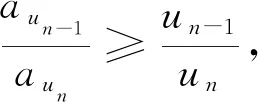

5 结束语
