冻融循环下含砂粉土冻胀率和融沉系数的试验研究

2021-11-04沈宇鹏邰博文汤天笑田亚护

铁道学报 2021年9期

沈宇鹏，刘越，邰博文，汤天笑，田亚护

(1.北京交通大学轨道工程北京市重点实验室，北京 100044；2.北京交通大学北京市轨道交通线路安全与防灾工程技术研究中心，北京 100044；3.中国科学院西北生态环境资源研究院冻土工程国家重点实验室，甘肃兰州 730000)

大量的现场监测资料表明，冻胀和融沉是多年冻土地区路基破坏的主要原因，以青藏公路为例，85%的填土路基病害是由于冻土的融沉造成的，其他15%的为冻胀和翻浆所致[1]。因此，研究土体在反复冻结、融化过程中物理力学性质的变化尤为重要，其中冻胀率和融沉系数随着冻融循环次数的变化规律对多年冻土区路基冻害预报和防控具有重要的工程指导意义。

20世纪30年代，国内外学者开始重视冻土的融化沉降问题。Morgenstern等[2]和Shoop等[3]提出了融沉计算模型，取得了良好的效果。Klinova等[4]通过室内试验，研究了融沉系数与干密度、含水率、孔隙率之间的相互关系。Tanaka等[5]通过室内大比例模型试验，研究了土体的融沉特性。吴李舟等[6]通过冻胀融沉试验，分析了非饱和黏土的冻胀融沉变化特征，研究了冻胀过程中冻结锋面的移动规律。刘鸿绪等[7]认为冻胀量是冻胀率沿冻结深度的叠加。随着研究的深入，冻融循环条件下融沉系数和冻胀率的变化规律引起学者的注意。梁波等[8]通过室内试验研究了不同土质在不同含水率、密实度、荷载条件下反复冻融过程中的融沉特性，并给出了反复冻融条件下融沉系数的表达式。严晗等[9]通过粉砂土一维开放反复冻融试验，研究了干密度、含水率、荷载以及冻融循环次数对冻胀率和融沉系数的影响，得到随着冻融循环次数增加，冻胀率及融沉系数先增大后减小，并在冻融4次后达到稳定。文献[10-11]认为荷载在抑制冻胀的同时也加剧了融沉，且得出经过多次冻融后，存在一个稳定的初始临界压实度。郑美玉[12]针对粉黏土进行多组冻融试验，得出含水率、冻结温度与融沉系数呈线性正相关，干密度与融沉系数呈线性负相关。王贺等[13]基于不同土质、泊松比以及温度影响下的冰水相变速率，分析了冻胀系数与土体冻胀率的相对关系。文献[14-17]将融沉分为非饱和、饱和以及过饱和3种状态来分析，并分别给出了3个状态下的融沉系数计算公式，与实测结果对比效果良好。

综上所述，国内外学者对冻融循环条件下土体冻胀率和融沉系数的变化规律及影响因素已经有了初步的认识，得到了一些公认的结论。但对青藏高原含砂粉土在封闭系统下冻胀率和融沉系数的研究较欠缺；且没有对冻融循环后冻胀率和融沉系数的稳定值进行系统的分析研究。因此，本文以青藏高原含砂粉土为研究对象，探讨不同含水率、压实度、荷载条件下含砂粉土在冻融循环过程中冻胀率和融沉系数的变化特征，进而建立稳定冻胀率和稳定融沉系数预测模型，进一步为多年冻土区路基融沉变形的精确预测提供理论基础。

1 室内试验

1.1 土的基本试验

本试验土样取自共(和)—玉(树)高速玛多段，对该土样进行土力学基本试验，并根据JTG 3430—2020《公路土工试验规程》[18]进行具体的试验操作。颗粒分析曲线见图1。小于0.075 mm颗粒的质量达到总土质量的10%以上，在筛分试验后对土样中小于0.075 mm的部分进行了密度计试验。

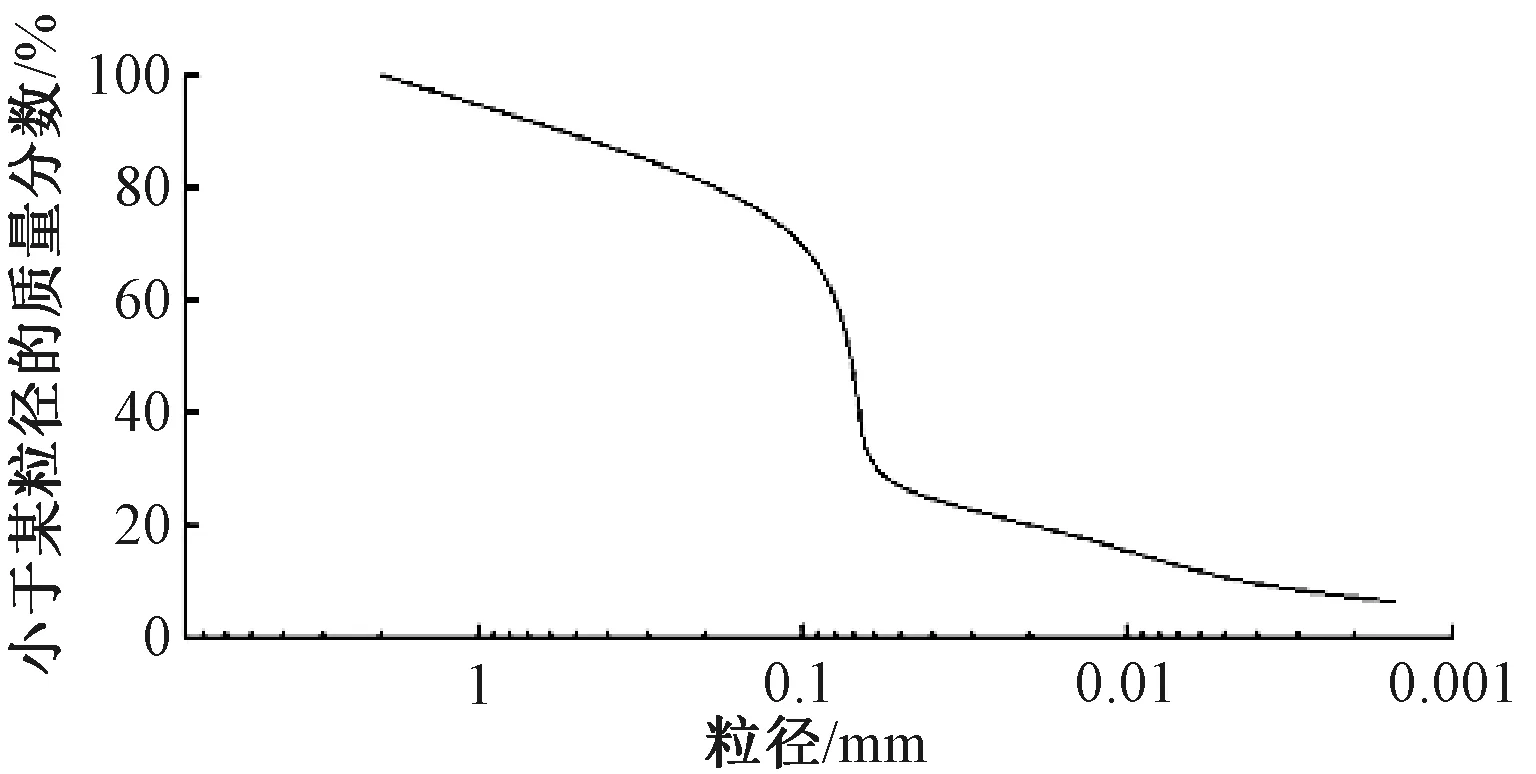
图1 颗粒分析曲线

由图1可知，土样的颗粒粒径均在2 mm以下，且小于0.075 mm颗粒的质量占总质量的55.6%。经过计算可得到试验土样的不均匀系数Cu=20.67，曲率系数Cc=6.28>3，土样属于级配不良土，压实难度大，工程性质差。此外，通过土粒比重试验及界限含水率试验得到土粒比重及界限含水率见表1。

表1 试验土样的界限含水率及土粒比重

参考JTG 3430—2020《公路土工试验规程》[18]的土样分类标准，可定义本试验土样为含粗粒(砂)的低液限粉土(ML)。

为测定含砂粉土在标准击实功作用下含水率与干密度之间的关系，对试验所用土样进行轻型击实试验。含砂粉土的击实试验曲线见图2。由图2可知，该土样的最优含水率ωOPT为13.2%，最大干密度ρdmax为1.766 g/cm3。

图2 试验土样的击实试验曲线

1.2 室内冻融试验方案

采用北京交通大学冻土实验室的高精度冻融循环试验箱开展反复冻融试验。采用重塑土进行试验，试验容器为直径10 cm、高15 cm的钢桶，将土样装入试验容器中，得试样直径10 cm、高12 cm。试验中将试样放置于-10 ℃的试验箱下冻结12 h，然后将试验箱温度调至10 ℃的恒温下融化12 h，反复这一过程来模拟冻融循环。试验为封闭条件下的冻融试验，即不考虑试样的补水情况。

本文分别研究压实度、含水率、荷载对含砂粉土冻胀率和融沉系数的影响，各因素取值如下：

(1)含水率和荷载不变，压实度分别取0.90、0.93、0.95。

(2)压实度和荷载不变，含水率分别取7.0%、13.2%、16.2%、20.2%。

(3)压实度和含水率不变，荷载分别取0、1.0、1.5、2.0 kPa。

具体试验方案见表2。

表2 试验方案

2 冻胀率试验结果分析

2.1 压实度对冻胀率的影响

在荷载0 kPa、含水率20.2%和荷载1.0 kPa、含水率20.2%的条件下对不同压实度土样进行试验，冻胀率试验结果见图3。

图3 试验试样在不同荷载和含水率条件下不同压实度冻胀率随冻融次数的变化规律

由图3可知，在荷载0 kPa、含水率20.2%情况下，随着冻融次数的增加，不同压实度土样的冻胀率先增大后减小，且均在6 次冻融后，冻胀率基本保持稳定值，其中在经过3 次冻融后，均可得到最大冻胀率，且随压实度的增大，试样的冻胀率降低；由图3(b)可知，不同压实度土样的冻胀率变化规律与图3(a)试验结果相似，且最大冻胀率同样出现在第 3 次冻融后，试样的冻胀率同样随着压实度的增大而降低。综上所述，在其他条件相同时，试样的冻胀率随压实度的增大而降低。

2.2 含水率对冻胀率的影响

水分是诱发土样冻胀融沉的根本因素。因此，开展荷载0 kPa、压实度0.90和荷载1.0 kPa、压实度0.90的条件下不同含水率土样的试验，冻胀率试验结果见图4。

由图4(a)可知，含水率较高时(16.2%和20.2%)随着冻融次数的增加，试样的冻胀率先增大后减小，并在经历 6～8 次冻融后冻胀率基本保持稳定值，且均在第 3 次冻融后得到最大值，含水率20.2%的冻胀率大于含水率16.2%的情况。含水率较低时(13.2%和7%)试样的冻胀率较小，均低于0.5%，且没有明显的变化规律。由图4(b)可知，试样的冻胀率变化规律与图4(a)基本相同。综上所述，初始含水率的越高，土体的冻胀率越大且规律性越明显。

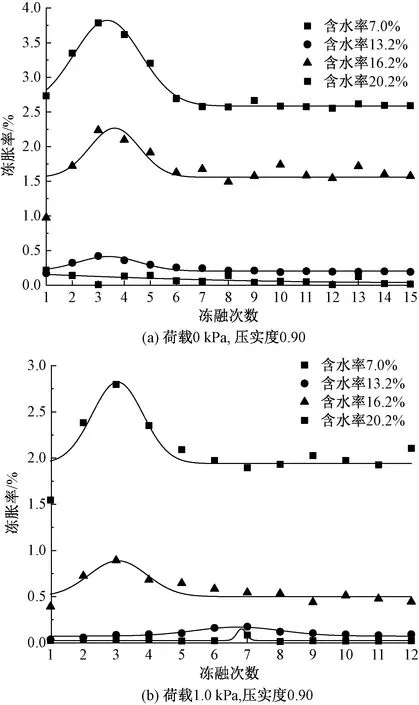
图4 试验试样在不同压实度和荷载条件下不同压实度冻胀率随冻融次数的变化

2.3 荷载对冻胀率的影响

荷载对土体压密有增强作用，即荷载不仅能减弱土体的冻胀变形同时促进了融沉变形。为进一步研究荷载对土体融沉系数的影响，本文保持压实度0.90、含水率20.2%的条件不变，分别将4组试样的荷载设置为0 、1.0、1.5、2.0 kPa，结果见图5。

图5 试验试样在压实度0.90、含水率20.2%条件下不同压实度冻胀率随冻融次数的变化

由图5可知,含水率20.2%、压实度0.90时，在自重和荷载作用下，随着冻融次数的增加，含砂粉土土样的冻胀率先增后减，在第3次冻融循环后达到冻胀率的最大值，经过6～8次冻融后，冻胀率保持基本稳定状态，冻胀率在达到稳定状态后，随荷载的增大，冻胀率减小。综上，试样的冻胀率随着荷载的增加而降低，这与图3、图4的变化趋势相吻合。

3 稳定冻胀率综合影响模型

不论试验初始条件如何，试样的冻胀率均随冻融次数的变化规律相似，均是随着冻融次数的增加，试验的冻胀率会先增后减，并在冻融6～8次后基本保持稳定状态，且冻胀率稳定值的大小与土样初始条件(压实度、含水率和荷载)有关，将该稳定值称为稳定冻胀率，用符号η∞表示。下面讨论各因素对稳定冻胀率η∞值的影响。

3.1 含水率对稳定冻胀率的影响

分析2节试验结果可知，不同含水率砂粉土的稳定冻胀率见表3。将两种不同初始条件的稳定冻胀率与含水率进行线性拟合，见图6。由图6可知，在初始条件一定的情况下，稳定冻胀率与含水率呈线性正相关。

表3 粉砂土在不同含水率下的稳定冻胀率

土体在经过多次冻融循环后，含水率存在一个临界值，将这一临界值定义为稳定冻胀率零值，认为当土体的含水率低于稳定冻胀率零值时，土体将不再出现冻胀现象。不同含水率下稳定冻胀率回归曲线见图6。在图6中，稳定冻胀率为零时对应的含水率是该初始条件下土样的稳定冻胀率零值。稳定冻胀率零值与试样的初始条件有关，如含水率、干密度和荷载。由图6可知，在0 kPa、压实度0.90条件下稳定冻胀率零值为12.23%；在1.0 kPa、压实度0.90条件下稳定冻胀率零值为13.54%。由此可得，随着荷载的增大，稳定冻胀率零值增大。

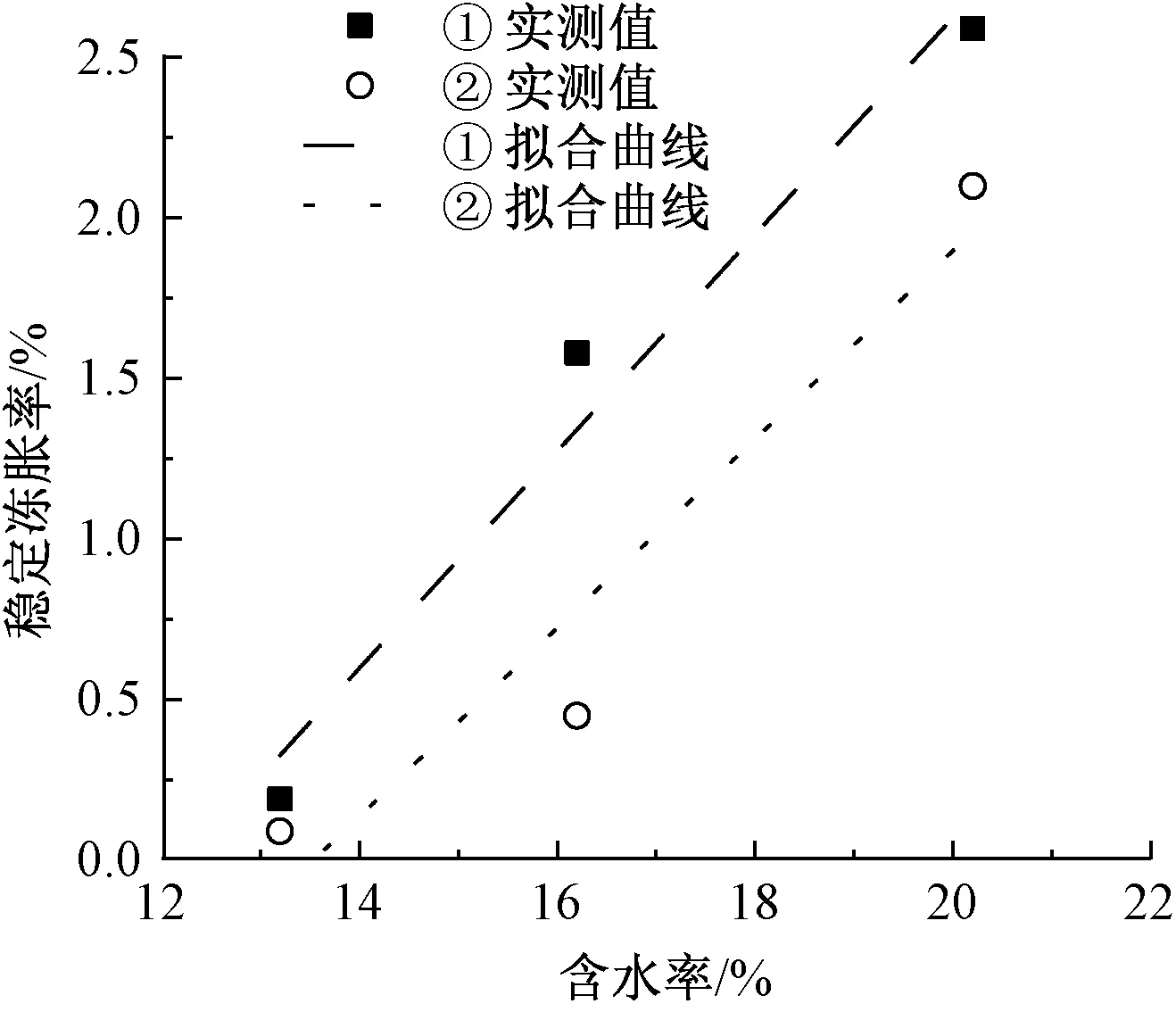
图6 不同含水率下稳定冻胀率回归曲线

3.2 压实度对稳定冻胀率的影响

同理，综合试验结果可得含砂粉土在不同压实度时的稳定冻胀率，见表4。将两种条件下稳定冻胀率与压实度进行线性拟合，见图7。在初始条件一定的情况下，稳定冻胀率与压实度呈线性负相关。

表4 不同压实度下稳定冻胀率

图7 不同压实度下稳定冻胀率回归曲线

3.3 荷载对稳定冻胀率的影响

同理可得，含砂粉土在不同荷载时的稳定冻胀率见表5。并将两种条件下的稳定冻胀率与荷载值进行线性拟合，见图8。由图8可知，保持初始条件不变，冻胀率的稳定值与荷载呈线性负相关。这是因为随着土样所受荷载的增加，土样压密作用增大，孔隙率减小，同时土样干密度变大，从而导致冻胀率降低。

表5 含砂粉土在不同荷载下的稳定冻胀率

图8 不同荷载下稳定冻胀率回归曲线

3.4 综合影响模型

综合稳定冻胀率试验结果，土体稳定冻胀率均与含水率、压实度和荷载呈线性规律，因此建立相加模型预测土体稳定冻胀率为

η∞=af(w)+bf(k)+cf(p)+d

(1)

式中：f(w)为土体含水率；f(k)为土体压实度；f(p)为土体所承担荷载；a,b,c均为不同因素的加权系数；d为计算系数。

结合不同压实度、荷载、含水率下的稳定融沉系数值，结合Levenberg-Marquardt法及全局优化法，通过优化计算得到：a= 0.303,b= -10.559,c= -0.633,d= 5.954。

代入式(1)中可得含砂粉土稳定冻胀率，稳定冻胀率实测值与相加模型计算值的比较曲线见图9。含水率较低时(7%)试样(试验编号1和7)的冻胀率和融沉系数较低，且没有明显的变化规律，所以在与实测值对比中舍去，剩余12组。由图9可知，实测值与计算值吻合性较好，表明稳定冻胀率预测模型可用来对含砂粉土稳定冻胀率进行预测。

图9 稳定冻胀率计算值与实测值对比

4 融沉系数试验结果分析

冻融循环下试样融沉系数的变化规律与冻胀率似，分析方法也相同。

4.1 压实度对融沉系数的影响

从荷载0 kPa、含水率20.2%和荷载1.0 kPa、含水率20.2%的条件下对不同压实度土样进行试验，试验结果见图10。

图10 试验试样在不同荷载条件下不同压实度融沉系数随冻融次数的变化

由图10(a)可知，不同压实度土样的融沉系数均在第3次冻融后达到最大值，在6～8次冻融后达到稳定状态，融沉系数随冻融次数增加先增大后减小，且随压实度的增大，试样的融沉系数降低。由图10(b)可知，不同压实度土样的融沉系数与由图10(a)的变化规律基本相同。综上所述，在其他条件相同时，试样的融沉系数随压实度的增大而降低。

4.2 含水率对融沉系数的影响

分别在荷载0 kPa、压实度0.90和荷载1 kPa、压实度0.90的条件下对不同含水率的土样进行试验，试验结果见图11。

图11 试验试样在不同荷载条件下不同含水率融沉系数随冻融次数的变化

由图11(a)可知，当含水率较高(16.2%和20.2%)时，随着冻融次数的增加，融沉系数先增大，并在第 3 次冻融后达到最大值，后减小，且在经历 6～8 次冻融后融沉系数基本保持稳定值。同时，融沉系数在含水率20.2%时的稳定值大于含水率为16.2%的稳定值；当土样含水率较低时(13.2%和7%)融沉系数小于0.5%，且未表现出明显规律性；由图11(b)可知，在土样荷载1 kPa、压实度0.90的条件下，试样的融沉系数变化规律与图11(a)基本相同。综上所述，初始含水率越高，土体的融沉系数越大且规律性越明显。

4.3 荷载对融沉系数的影响

保持试样压实度0.90、含水率20.2%的条件不变，将四组试样的荷载分别设置为0、1.0、1.5、2.0 kPa，进行对比试验，试验结果见图12。

由图12可知，含砂粉土在自重和荷载作用下，随着冻融次数的增加，融沉系数先增大并在第3次冻融后达到最大值，后减小，且在经历 6～8 次冻融后基本趋于稳定，稳定后的融沉系数随荷载的增加而减小，即随着荷载的增加，试样的融沉系数降低。

图12 试验试样在压实度0.90、含水率20.2%条件下不同压实度融沉系数随冻融次数的变化

5 稳定融沉系数综合影响模型

与稳定冻胀率类似，在冻融循环6～8次后试样融沉系数也基本保持稳定值，同时稳定值的大小与土样的初始条件(压实度、含水率和荷载)有关，将该稳定值称为稳定融沉系数，用符号A∞表示。因此，讨论各因素对稳定融沉系数A∞的影响。

5.1 含水率对稳定融沉系数的影响

综合以上试验结果，可以得到含砂粉土在不同含水率时的稳定融沉系数见表6。将两种不同初始条件的稳定融沉系数与含水率进行线性拟合，拟合结果见图13。由图13可知，在初始条件一定的情况下，稳定融沉系数与含水率呈线性正相关。

表6 粉砂土在不同含水率下的稳定融沉系数

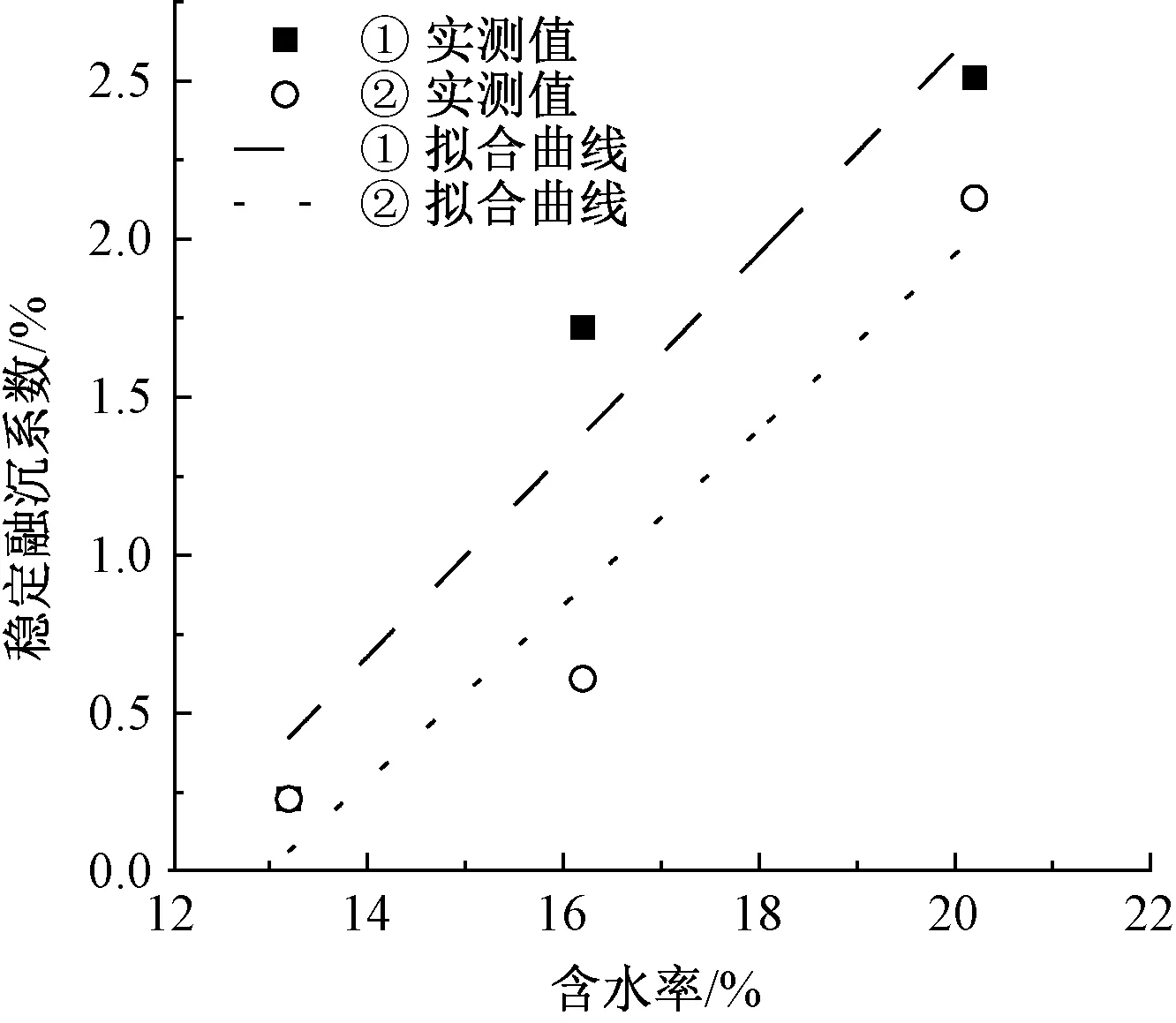
图13 不同含水率下稳定融沉系数回归曲线

与稳定冻胀率零值一样，对于多次冻融循环的土体的稳定融沉系数，存在一个稳定的稳定融沉系数零值。由图13可知,在0 kPa、压实度0.90条件下稳定融沉系数零值为11.87%；在1 kPa、压实度0.90条件下稳定冻胀率零值为12.95%。由此可得，随荷载的增大，稳定冻胀率零值增大。

5.2 压实度对稳定融沉系数的影响

同理可得在不同压实度下含砂粉土的稳定融沉系数，见表7。分别将两种条件下稳定融沉系数与压实度进行线性拟合，见图14。由图14可知，在初始条件一定的情况下，稳定融沉系数与压实度呈线性负相关。

表7 稳定融沉系数在不同压实度下的变化

图14 不同压实度下稳定融沉系数回归曲线

压实度变化引起的土体稳定融沉系数变化是原因：由于当土体的压实度较小时，孔隙率较大，冻结后土体的沉降量除了自重以及荷载作用引起的沉降外，还包括土体发生融化时冻土中的部分冰相变为水的体积减小量，综合导致在土体压实度较小时，稳定融沉系数偏大的现象；当土体的压实度较大时，孔隙率较小，同时干密度增大，因此土体自重及荷载作用引起的沉降量减小，所以在土体压实度较大时，稳定融沉系数偏小。综合上所述，结合实际工况，认为增加路基压实度能够有效地提高施工质量和减小融沉病害。