基于改进型构筑算法对城轨车载蓄电池系统优化研究

曹雪铭，黄 健，张言茹，姜 君，姜 伟

(1.中国铁道科学研究院 研究生部，北京 10081；2.中国铁道科学研究院集团有限公司 标准计量研究所，北京10081；3.北京交通大学 电气工程学院，北京 10044)

随着国家“十三五”规划提出的创新、协调、绿色、开放、共享这五大发展理念的不断深入实践，为满足城市轨道交通车辆装备质量的不断提高、创新的要求，我国轨道交通行业正在不断加大各类节能设备的投入，虽然已经取得一些进展，但仍有很大空间值得探索。

目前国内主流的城轨节能设备均以地面节能系统为主，其原理是将车辆制动的能量转换为电能以便再次利用，根据系统的构成可分为回网式与储能式。其中回网式系统是将车辆制动的能量直接回馈电网，优点是制造及维护成本相对较低，功率密度相对较高，有一定的寿命优势，但是其节能效果受发车间隔、电网负载等因素的影响较大，并且整流变压器的体积质量较大。储能式系统是将车辆制动时产生的能量存储在储能元件中，如电容、电池、飞轮储能，其优点是电能的二次利用可控，具有较高的节能率，但是其相对制造成本较高，功率密度相对较低[1]。

以上无论哪种方案，通常只有在车辆制动时的网压达到阈值时才开始工作，所以存在较大的能量损失，延长了收回节能成本的时间。

目前城轨车辆正常运营时，车载蓄电池通常仅工作在浮充状态，且因镉镍和铅酸等电池的质量较大，造成了大量的行驶能量浪费。目前无论充电机还是蓄电池，都已经难以满足高效节能的需求。

近年来，国内外也逐步开展了关于轨道车辆车载储能系统的研究，但主要集中在配置优化与寿命的研究上，如文献[2-4]采用雨流计数法建立了多工况下储能元件寿命的预测模型，并利用遗传算法对此配置模型进行寻优求解，文献[5-7]研究了混合动力模型下，车载储能元件的能量规划模型，通过不同工况下能量的分配，达到储能元件寿命的最优解。

本文将结合城轨车辆运行工况，从车载储能系统拓扑与充放电策略两方面，以提高车载蓄电池系统的利用率为目标，建立储能元件效率模型，对车载储能系统进行优化改进。

1 蓄电池与充电机选型

目前以镉镍碱性蓄电池或铅酸蓄电池为主，容量通常为120～180 Ah。车载充电机作为单向充电器，在给蓄电池充电时，通过检测蓄电池电压及温度的变化改变输出电压，同时利用电流限制措施，限制充电电流，确保蓄电池的使用寿命。镉镍碱性蓄电池和铅酸蓄电池虽然价格较低，维护方便，也有较高的安全性，但是并没有配备电池管理系统(BMS)，额定功率相对较低，并不具备大功率充放电的特性。单向充电机也并没有将电池荷电状态加入闭环控制环节，难以实现频繁高倍率动态充放电控制。

随着锂电池技术的发展，为了提高蓄电池系统的使用频率与车辆频繁的牵引和制动工况相适应，车载蓄电池也应考虑使用功率型电池，如锂电池或电容混合型电池。

目前市场上主流的锂电池根据化学特性一般分为磷酸铁锂电池、三元锂电池、锰酸锂电池以及钛酸锂电池，其单体电池基本属性见表1[8]。单体电池特性如表1中所示，但其成组数量也同样影响着系统的可靠性与安全性，过多的单体电池会使得整个系统的可靠性与寿命下降。在电池成组时，也应确保安全风险发生概率降低到可接受范围。

表1 主流功率型锂电池关键属性对比

目前城轨车载充电机的工作原理是将辅助变流器输出的交流电源(AC380 V)整流为低压直流电源(DC110 V)，在为车载蓄电池浮充的同时也为车载低压直流照明与控制装置提供电能。

低压辅助供电系统中辅助变流器(SIV)保证了电池与接触网的两级隔离，不仅可以减少网压波动对充电机的影响，也可提高蓄电池组的安全性与稳定性，所以可以保持现在的低压辅助供电系统的拓扑结构。而为了充电机能够快速响应车辆运行中的各种复杂工况，可以使用PWM高频变换器作为车载蓄电池的充电机，因其具有响应快、体积小、效率高的先天优势，与传统的充电机相比，可实现网侧单位功率因数和正弦波电流控制，使电能双向传输，实现四象限运行[9]。

2 蓄电池充放电基本策略模型

目前的制动储能策略一般分为两类：①以车辆牵引和制动为信号，这一类策略虽然能做到储能最大化，但是并没有对充放电损耗及电池组状态进行充分考虑，也并不能剔除一些效率较低的不适工况，频繁的启动不仅会增加器件的损耗，也会影响系统稳定性；②以接触网电压为阈值，达到设定电压值后，储能装置立即进行充放电动作，这类控制策略虽然能够提高系统的稳定性，但是阈值受实际线路影响，前期调试复杂，并且很难达到储能的最优化。

车载蓄电池不同于地面储能系统，受体积及质量的限制，很难提供牵引和制动时所需的全部功率及能量，所以应构建与之相适应控制策略，使其能在有限的功率及充放电时间内，达到能效最大化。

因为城轨车辆具有运行线路固定，牵引和制动工况交替频繁的特点，所以车载蓄电池系统的基本充放电策略是在车辆牵引和惰行工况下为车载辅助设备供电(AC380 V)，并在车辆制动时为电池充电，控制的目标是有效捕捉每一次制动，尽可能在较高的效率点下给电池组进行充电，基本供电模型与控制逻辑见图1。

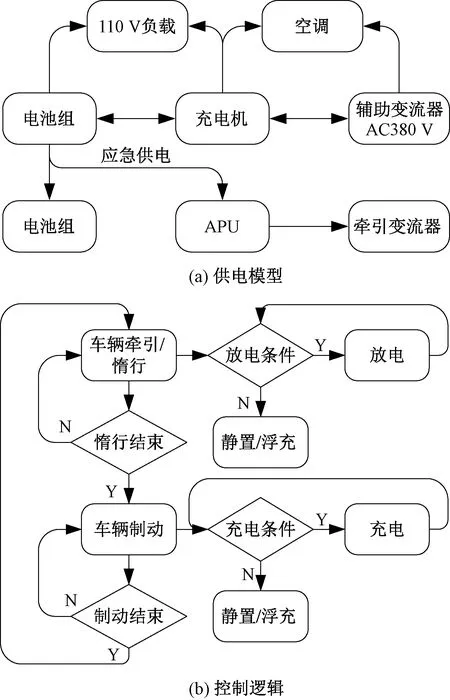
图1 车载蓄电池供电模型与控制逻辑

对于功率远小于牵引逆变器功率的蓄电池系统，工况预测的目标是每一次制动时的功率与时长，而城轨车辆的功率需求曲线通常十分规律，在车辆运行之前即可通过计算得出，这使得对未来每一个时刻的车辆功率需求变为已知，通过该功率曲线可在各区间内将能量进行分配控制，建立电池组电量SOC目标区间，见图2[10]。

图2 站间电池组状态曲线

对于SOC控制区间的选取，考虑到电池组有可能作为应急备用电源，所以图2中SOC的控制区间的上限SOCH应在留出过充电余量的同时，尽量选取在SOC的高点，控制区间的下限SOCL可根据电池容量、峰值电流及预计充放电持续时间综合计算。

(1)

式中：α为防止过充电预留上限；Pmax为最大放电功率；Tmax为最大放电时间；Cbat为电池容量额定值；Vocv为电池标称开路电压。

假设车辆仅在制动过程对电池进行充电，可将充电过程作为目标函数，即

f(SOC)=w(F,t)=g(P,t)

(2)

式中：F为车辆牵引力;P为充电功率；w为车辆牵引力函数；g为车辆牵引电功率函数。该函数将电池组能量控制策略问题转化为功率控制策略问题，通过车辆牵引制动的功率与时间对电池组的SOC进行计算，并通过优化使系统的转化效率最大化。一般充电机效率的计算可通过输出与输入功率的比值得出，蓄电池的充放电效率定义为释放能量和吸收能量之比，为了分析系统损耗，也可从储能元件功率损耗角度考虑，综合计算系统瞬时效率[11]

(3)

式中：ηcharge、ηdischarge分别为充、放电效率；PDC为充电机直流侧功率；PAC为充电机交流侧功率；Ploss为该功率下蓄电池损耗，主要由热损耗及散热损耗构成。

蓄(锂)电池在正常充放电过程中产生的损耗主要由热损耗构成，其中可分为反应热、焦耳热、极化热、副反应热，实际处理中往往将副反应热忽略不计。多数锂电池充电时属吸热反应，放电时为放热反应，两者都包含内阻热耗。充电初期，极化电阻最小，吸热反应处于主导地位，电池温升可能出现负值，充电后期，阻抗增大，释热多于吸热，温升增加[12]。

Bernadi等[13]基于内部物体发热均匀假设，提出了一种热生成理论计算式

(4)

QP=I2RΩ

QB=Ah(Tcell-TA)

式中：Ccell为电池的质量热容折算系数；Tcell为电池表面温度；QP为内阻产热;RΩ为电池等效内阻；QS为热熵变化;dE/dT为热熵系数；I为电流,充电时I为正，放电时I为负；QB为传导热;A为热传导系数；h为电池表面积；TA为环境温度。考虑到强迫散热，将方程离散化后，有

(5)

其中，Tt(k)为k时刻电池温度，k∈N；Δt为采样时间间隔；Pf为散热功率。实际上电池的温升与电池的工况是一个十分复杂的关系，温度过低会增大电池的内阻，温度过高不仅影响使用寿命，也需要更耗费高功率的散热器件，所以控制蓄电池温升也是优化的重要因素。

为了简化模型，可建立工况区间离散热量-损耗模型QT(k)(It(k)，(dE/dT)t(k))作为充放电温度控制的约束函数。

(6)

式中：n=t/Δt，t为每次充电、放电及浮充工况持续时间；QT，n为第n次充放电时电池的热量损耗。为了便于电池组充放电策略优化，对损耗进行最优计算，可将PAC作为目标变量，当蓄电池系统放电功率小于辅助系统供电所需功率时，若经过n次充电，m次放电，有

约束函数：s.t.

(7)

式中：tcharge、tdischarge分别为充、放电持续时间；γ为保护截止热限值。将电池组的能量控制策略问题转化为功率及损耗控制问题，其约束条件为总充入电量约等于总放出电量，充电功率小于制动提供的最大功率及充电机的最大功率，放电功率小于充电机的最大功率。此模型可直观地将充放电效率与SOC建立函数关系，为进一步优化提供了数学模型。

3 充放电策略模型的优化

3.1 模型的优化

相对于精确解算法，构筑算法对于快速求解大规模现实问题具有很强的实用性，但传统的构筑算法一般采取逐步构造解的方法，即逐一地为所有决策变量赋值，每次增加解的一个元素，在每一步都是做出当时的最佳移动，经过有限次循环，直到得到一个完整的满意解[14]。由于电池的状态具有滞后性与传递性，为了避免短期的贪婪行为，本文在探索途中加入能量评估向量函数Φj(ΔSOC，ΔQT)辅助下一步探索，改进型构筑算法见图4。

图3 改进构筑算法示意图

对于模型的优化即是对其寻求最优解的过程，可将式(4)分割成充电模型与放电模型分别进行优化求解，通过控制放电时的功率点与时长，使系统在放电时达到最低能耗与最小温升，且为下一次充电预留足够的可充电余量，使蓄电池的SOC持续保持在目标SOC区间内。分割后，对于充电模型选取最大充电量模型，将时间曲线函数离散化，若第i次充电持续时间为tcharge，i，则ti=tcharge，i/Δt，ti∈N。

Charge-n(共计i次放电)目标函数可为

maxΔSOC(PAC，tcharge)

约束函数：s.t.

(8)

式中：Pbreak为制动功率；ΔSOC为实际充入的电量，由充电功率PAC、转换效率ηcharge及充电时间tcharge决定。

同理，对于放电模型选取最小放电损耗模型，构造二维损耗向量Qdis,j(Qloss，j，QT，j)，Qloss，j为第j次放电损耗的电能，QT，j为第j次放电产生的热能，则目标函数为该二维向量模的和最小。

Discharge，m(共计j次放电)目标函数为

离散化后，若第j次放电持续时间为tcharge，j，则tj=tcharge，j/Δt，tj∈N,有

有约束函数：s.t.

(9)

式中：RΩ为电池内阻；tdisMax，j为第j次放电最多可持续时间；tdischarge，j为第j次放电持续时间；PAC，a为第i次充电过程中第a秒充电功率，对应效率为ηcharge，a。

根据改进型构筑算法，其伪代码为：

输入：第i次制动持续时间tcharge，i；第i次充电过程中第a秒充电功率PAC，a及对应效率ηcharge，a；第j次可放电最长时间tdisMax，j；第j次放电过程中第β秒充放电功率PAC，β及对应效率ηcharge，β；评估向量函数Φi，设置评估函数终止限值α，γ(防止过充过温)。

Step1初始化i=1，j=1，Φ0=(0,0)

Step2计算第i次制动，最大充入电量ΔSOCi及充电发热量QT，i为

决策变量为PAC，a≤Pmax，tdischarge≤tdisMax

Step3对放电效率进行排序：

排序ηdischarge,k(I)：fork=1 ton,k←1

Step4计算第j次放电的|Qdis,k|并排序：

排序|Qdis,k|：fork=1 ton,k←1

Step5计算评估向量函数：

Φj=(ΔSOCj，QT，j)

if ΔSOCj≤α&&QT，j≤γ

elsek=k+1

Step6对下一次充放电优化计算，输出最优解：

i=i+1j=j+1

ifi>n&&j>m

then stop

else go to Step2

若某一次的评估向量函数Φi值达到终止限值，可适当降低初始状态SOC，使得下一次充电后电量不超过SOCH，再通过传递函数将电量余量传递到下一次放电中，再次达到SOC平衡。

3.2 模型的应用

对于最优解类问题，数据的选取对于模型的计算至关重要，过多的数据输入会带来更大的计算成本，数据过少有可能错过全局最优解。虽然城轨驾驶员可能会有不同的驾驶习惯，但是通过测量数据可以发现，同样线路下不同驾驶员对车辆工况影响十分有限。

为了便于计算，选取长沙地铁1号线车辆往返运营一次的单台牵引逆变器实测数据，功率曲线见图4。蓄电池组和双向充电机参数见表2[15-16]，将伪代码中所需输入量代入算法进行求解，再根据ΔQi及ΔQj描绘电池组的SOC曲线，以实现最优SOC目标区间控制。

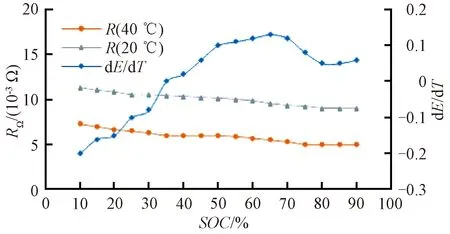
图4 锂电池内阻(dE/dT)-SOC曲线

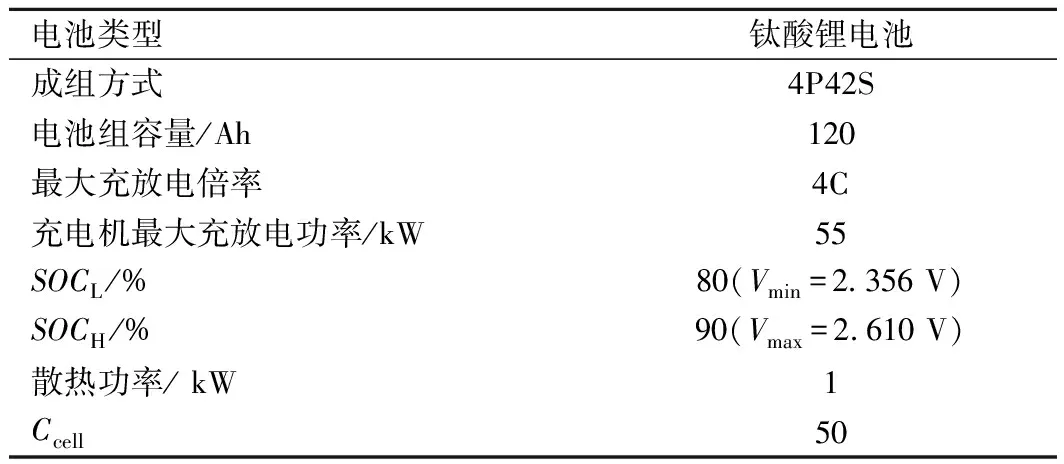
表2 蓄电池和双向充电机参数

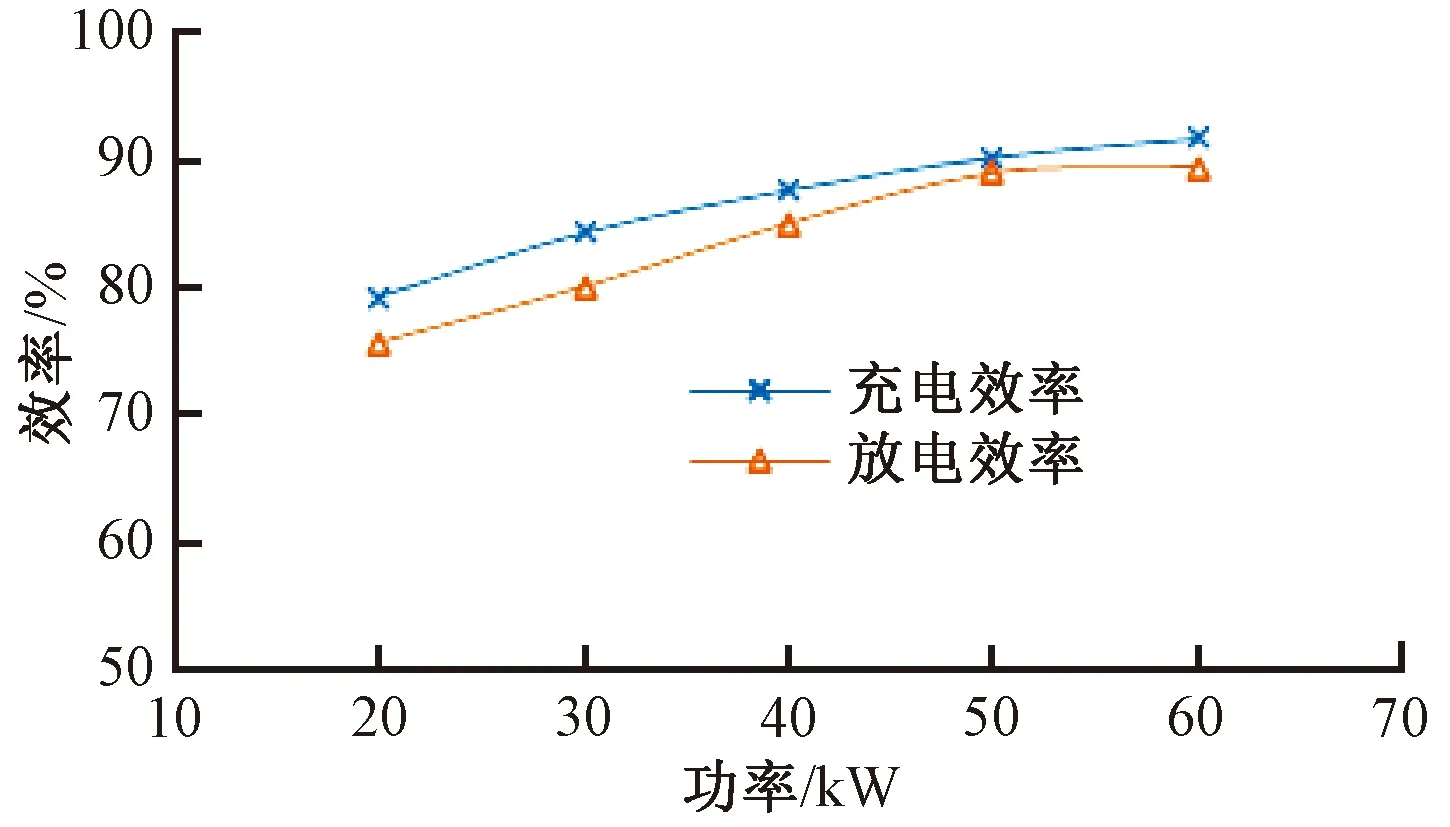
图5 充电机效率曲线

充放电策略计算结果见表3。牵引逆变器功率曲线见图6。由图6可见，通过改进型构筑算法计算后，蓄电池系统充放电功率曲线及SOC曲线见图7、图8。

表3 充放电策略计算结果

图6 牵引逆变器功率曲线(负半轴为制动功率)

图7 蓄电池系统充放电功率曲线

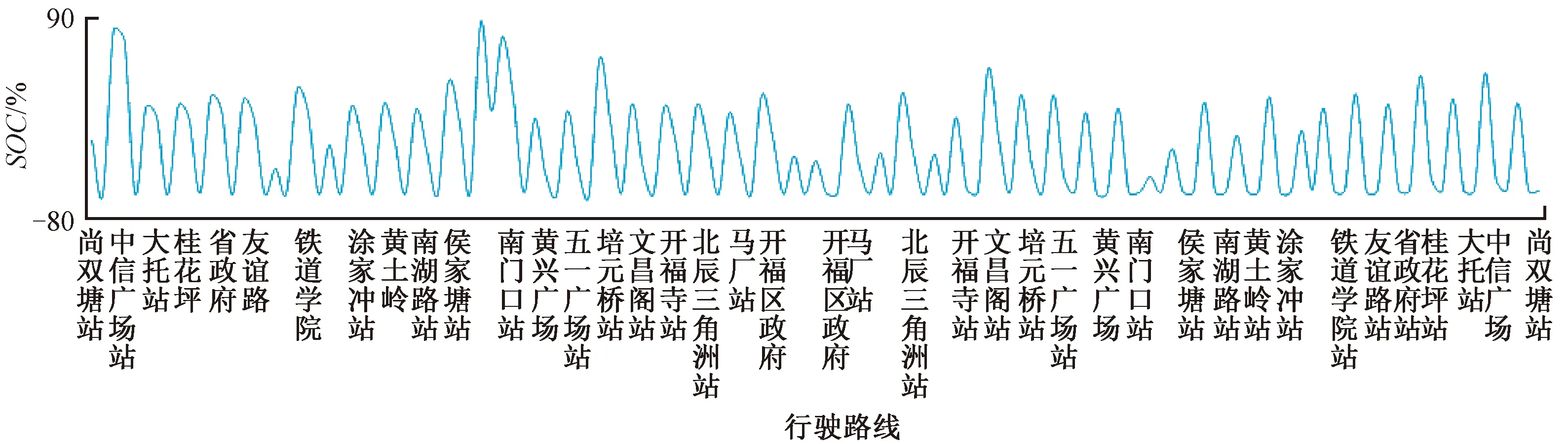
图8 站间SOC曲线

由表3可见，通过对蓄电池系统采取动态充放电策略，以改进型构筑算法对充放电模型进行控制，不仅可以有效控制电池组充放电SOC区间，也减少了车辆行驶损耗。且该线路车辆若搭载此蓄电池系统运行，系统单日理论节省电量可达200 kW·h，相较于该线路每日约5 000 kW·h/车的能耗，此优化方案节能效果十分显著。

4 结论

通过对城轨车辆蓄电池系统供电方式优化，采用四象限充电机，选取适当类型的蓄电池，并将传统的浮充控制策略优化为动态充放电策略，可大幅提高蓄电池的利用率。通过将蓄电池状态与充电机状态、车辆状态建立联系，分别建立充电、放电模型，分别以控制充电量、放电损耗为目标对模型进行优化控制，即可提高能量转化的效率，又可将电池组的SOC控制在目标区间内，防止电池滥用，确保蓄电池作为备用电源供电。

结合长沙地铁1号线的车辆牵引工况，以改进型构筑算法对模型进行了优化计算验证，结果显示此策略简单有效，极大地提高了蓄电池的使用效率，为车载蓄电池系统实现动态充放电提供了有效的理论依据。