桥梁构件三维地震易损性分析

2021-11-04单德山苑洁艺

铁道学报 2021年9期

单德山，苑洁艺，董俊，李乔

(1.西南交通大学土木工程学院，四川成都 610031；2.四川建筑职业技术学院，四川德阳 618000)

随着我国交通网络的不断更新，越来越多的公路与铁路规划、修建于西部地区，如藏区高速、雅西高速等公路，以及成兰线、川青线、丽香线等铁路。由于西部地区地势崎岖不平、山高谷深，位于该地区的桥梁结构属于典型的非规则桥梁，其地震响应具有明显的近场特点[1-3]。同时，我国西部地区涵盖较多地震带，受地震影响的范围分布广泛，其中的桥梁抗震性能需求显然高于其他地区[1]。如何合理、有效地评价该区域桥梁的抗震性能已受到诸多学者的关注与重视[2-3]。

目前，评估桥梁结构抗震性能普遍采用地震易损性分析，考虑的地震动多为水平单向地震作用(纵向或横向)，选用墩顶位移、曲率延性比、截面曲率、变形和能量双重指标等作为结构的损伤指标[4]。部分学者也开展了双向地震动(纵向+横向)作用下的易损性分析[5]，但仍采用仅能表征纵向或横向地震作用下结构损伤状态的损伤指标[6]，分别讨论纵、横向地震易损性分析，并未构建双向(或多向)地震同时作用下的损伤指标进行多向地震易损性分析。

目前，既有桥梁结构易损性分析方法多为一维地震易损性分析方法。董俊等[7]利用该方法对近、远场地震作用下的非规则桥梁地震易损性进行对比分析，得到两种情况下桥梁结构损伤概率偏差最大为15.6%，且近场地震作用下桥梁构件更容易受损的结论。Billah等[8]通过一维地震易损性方法探讨了近、远场地震作用下桥梁的抗震性能。

此外，近场桥梁不仅在水平地震作用下易损，在竖向地震作用也容易受损，常用的一维地震易损性分析方法已无法满足近场桥梁结构抗震性能评估的需求。目前，尚未见关于三维地震作用下桥梁地震易损性分析的研究。因此，为分析桥梁结构的三维地震易损性，本文以工程结构可靠度理论为基础，根据既有墩柱弯曲和剪切失效曲面的研究成果，采用墩柱的多个单向损伤指标构建其弯曲破坏和剪切破坏的损伤状态方程；基于支座滑移准则，建立包含多个单向损伤指标的支座损伤状态方程；随后根据此损伤状态方程建立墩柱和支座的三维地震损伤状态判别标准，并绘制构件三维失效曲面，以量化相应的损伤状态；最后基于IDA分析建立桥梁构件的三维易损性曲面，并与一维地震易损性结果进行对比，以验证所提方法的正确性和合理性。

1 结构三维地震易损性分析方法

1.1 基本思路

结构可靠度理论中，结构是否可靠取决于功能函数R：当R≥0时，结构可靠；当R<0时，则结构失效。此功能函数为结构需求和能力的数学函数，包含多个随机变量，又被称为状态方程，表示结构构件抵抗各种作用效应的能力[9]。

地震易损性中，结构的“失效”表示结构发生了指定的4种地震损伤状态，即轻微、中等、严重和倒塌破坏。从结构可靠度的角度而言，桥梁地震易损性分析的目的为得到给定地震作用下，桥梁结构状态方程小于0的概率。

桥梁抗震能力假设为Sc，其地震需求为Sd，对应的损伤状态方程R=Sc-Sd。若已知R<0的概率密度函数fR(R)，则其地震损伤概率为

(1)

若R服从σR分布，式(1)可改写为

(2)

令R=μR+σRt，即可得到桥梁结构地震损伤概率的计算公式为

(3)

式中：μR为结构状态方程的均值；σR为结构状态方程的标准差；β为结构可靠指标，由结构状态方程的均值μR和标准差σR计算得到。

由以上思路可知，为评估桥梁在三维地震作用下的抗震性能，首先需要定量判定结构的损伤情况，即构建结构在三维地震动作用下发生损伤状态方程，获得不同损伤状态所对应损伤指标临界值。

历史震害资料表明，墩柱和支座的损伤为桥梁结构的主要震害[10-12]。因此，本文通过建立墩柱和支座损伤状态方程来开展桥梁三维地震易损性分析。

1.2 墩柱损伤状态方程

墩柱地震损伤主要表现为弯曲破坏、弯剪破坏和剪切破坏[10-12]。墩柱的不同损伤方式直接影响桥梁结构的抗震能力，国内外学者围绕墩柱地震破坏方式及性能特点开展了广泛深入的研究，在墩柱弯曲和剪切破坏方面取得了丰硕的成果，墩柱弯剪破坏的相关研究还有待深入[5, 13]。本文仅依据相对成熟的剪切和弯曲破坏机理，开展桥梁墩柱弯曲和剪切破坏的地震易损性分析。

1.2.1 墩柱弯曲损伤状态方程

墩柱常用地震损伤指标(如曲率或曲率延性比)表征单向地震作用下的损伤状态，但不能准确描述三维地震作用下的损伤状态[4]。为分析墩柱的三维弯曲易损性，依据我国桥梁抗震规范[14]以及美国Caltrans抗震设计规范[15]的相关规定，采用墩柱偏压荷载作用下的失效屈服面[16]和钢筋混凝土构件剪切-轴压失效屈服面[17]构建墩柱弯曲破坏和剪切破坏的损伤状态方程，并结合文献[18-19]提出的墩柱抗剪承载力计算理论确定不同损伤状态的临界值。

墩柱双向弯矩及轴向力作用时的弯曲破坏准则[16]为

(4)

式中：P为地震作用引起的墩柱轴力；P0为地震作用引起的偏心距为0时的墩柱极限轴力；Pc分为墩柱发生平衡破坏时的极限轴力[20]；Mx、My分别为给定强度地震动作用下，墩柱绕两个惯性主轴x、y的抗弯需求；Mxu、Myu分别为轴力Pc作用下，墩柱x、y单轴偏压的抗弯能力；m、n、k分别为惯性主轴x、y方向的弯矩、轴力荷载指数，本文均取为2。

由式(4)即可得到地震作用下，墩柱的弯曲损伤状态方程为

Zi=f(P,Mx,My)=1-

(5)

式中：i=1,2,3,4分别对应轻微损伤、中等损伤、严重损伤、完全破坏4种地震损伤状态；Zi为第i种弯曲破坏状态对应的墩柱损伤状态方程；Mxu,i、Myu,i分别为损伤状态i时，墩柱截面x、y方向的抗弯能力，其值与Pc有关，由弯矩-曲率分析可得不同损伤状态的弯矩值。

为准确描述墩柱的延性能力，基于文献[15，19]给出的双线性近似弯矩-曲率关系，式(5)可写为

Zi=f(P,Mx,My)=1-

(6)

式中：φx、φy分别表示给定强度地震作用下，墩柱截面x、y方向的曲率需求；φxu,i、φyu,i分别损伤状态i的x、y方向的曲率延性指标，其值与Pc相关，可由弯矩-曲率分析得到[21]。

由式(6)可知，桥梁墩柱在给定地震动作用下是否发生指定的损伤状态，首先需要确定该损伤状态下P0、φxu,i和φyu,i的临界值，随后计算给定地震作用下墩柱所承受的P、φx、φy，最后根据式(6)计算得到Z的数值，若Z<0，则桥梁墩柱发生指定的弯曲损伤状态。

1.2.2 墩柱剪切损伤状态方程

国内外学者对往复荷载作用下，钢筋混凝土墩柱的抗剪强度进行了广泛深入的研究，并提出了不同的强度计算方法[17,22]。基于Vecchio等[17]提出的钢筋混凝土墩柱抗剪强度二次失效曲面，将墩柱的剪切损伤状态方程定义为

Gi=g(F,Vx,Vy)=1-

(7)

大量钢筋混凝土墩柱剪切破坏试验研究[18-19,23-27]表明：往复荷载作用下，墩柱剪切破坏经历完好→混凝土开裂→首条贯穿斜裂缝→多条贯穿斜裂缝→破坏共5个过程。为与弯曲破坏常用的完好、轻微、中度、严重和完全破坏5个损伤状态保持一致，定义了如表 1所示的墩柱剪切破坏准则。其中：Vc1、Vc、Vcs、Vu分别为墩柱发生轻微剪切损伤、中等剪切损伤、严重剪切损伤、弯曲剪切破坏时的抗剪强度临界值；Vc为墩柱出现第一条完整斜裂缝时的抗剪强度；Vu为墩柱的极限抗剪强度，其值可由文献[18-19]建议的计算公式得到。

表1 墩柱剪切破坏的损伤判别准则

基于Ricles等[28]和Galal等[29]的研究成果，将轻微剪切损伤的限值Vc1取为0.862倍Vc，严重剪切损伤的限值Vcs取为完全剪切破坏Vu和延性抗剪强度Vnd的均值，其中Vnd可由Priestley等[19]推荐的公式计算得到。由此可得到墩柱在双向剪力和轴力作用下，4种地震损伤状态的关系如图 1所示。

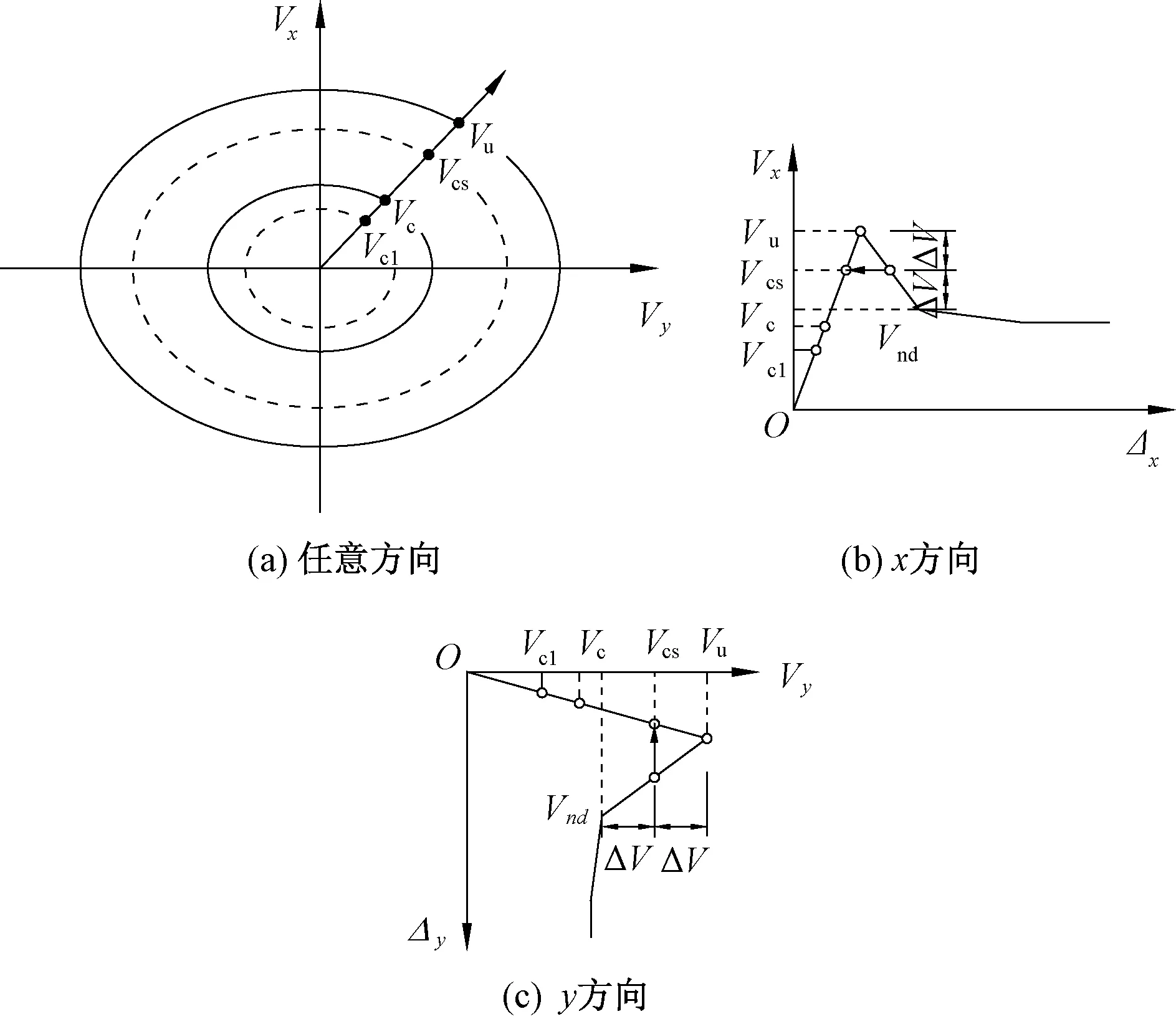
图1 墩柱各剪切损伤状态的关系曲线

1.3 支座损伤状态方程

支座的地震损伤可由支座上下垫板的相对变形进行表征，在进行桥梁三维地震易损性分析时，将支座损伤指标取为支座上下垫板间的相对位移，且该损伤指标应能给出任意方向上下垫板间相对位移与损伤状态间的关系。

基于Jangid[30]建立的支座滑移准则，构建支座损伤状态方程为

(8)

与墩柱类似，根据支座上下垫板的相对位移也定义了4种支座地震损伤状态，图 2给出了支座的4中纵向损伤状态，表 2为对应的损伤描述和损伤指标。其中：ds为支座设计位移值；dm为球冠衬板左缘到上支座板左缘的距离；de为球冠衬板中心到上支座板左缘的距离；dc为球冠衬板右缘到上支座板左缘的距离。

图2 支座不同损伤状态示意图

表2 支座纵桥向地震损伤判别

1.4 桥梁结构三维地震易损性计算

由1.1节的基本思路可知，在任意方向三维地震作用下，将动力响应的极值代入损伤状态方程式(6)～式(8)，即可获得该构件的状态，包括是否出现了地震损伤及其状态。

图 3为桥梁三维地震易损性分析流程，采用N条不同强度的地震动对桥梁结构进行地震响应时程分析，依据各构件的状态方程获得所需的动力响应极值后，得到状态方程的均值μR和标准差σR，并代入式(3)即可计算出给定地震动强度下桥梁构件的地震损伤概率。

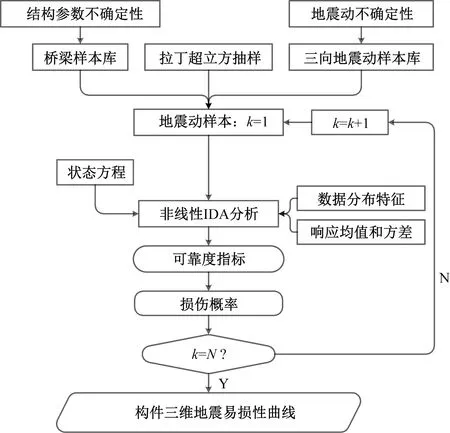
图3 桥梁三维地震易损性分析流程

桥梁结构三维地震易损性分析时，其墩柱地震弯曲损伤、剪切损伤和支座损伤的状态方程均为多元非线性方程，以墩柱弯曲损伤为例说明其可靠度指标的计算过程。

将三元非线性状态方程(6)改写为

(9)

式中：i=1,2,3,4分别对应轻微损伤、中等损伤、严重损伤和完全破坏；m1、m2、m3分别为状态方程的系数，m1=[1/(P0-Pc)]2、m2=(1/φxu,i)2、m3=(1/φyu,i)2。在单条地震动下，假设墩柱截面抗震需求为(Pj,φx,j,φy,j)T，j=1,2,…,N，并近似服从对数正态分布，N为地震动数量，墩柱抗震需求的均值为μ1、μ2、μ3，其标准差为σ1、σ2、σ3，则墩柱的可靠度指标可利用验算点方法[31]计算得到。

得到构件易损性分析结果后，可按可靠度理论计算桥梁结构构件的损伤概率[31-32]，据此完成桥梁构件三维地震易损性分析。

2 桥梁构件三维地震易损性分析

2.1 工程概况

为验证本文所提的桥梁结构三维易损性分析方法，本文以某大跨高墩刚构-连续桥为例进行论证。该组合桥的跨径组成为(68+2×120+68+3×32+24) m，主桥为4跨高墩大跨刚构-连续组合体系，其反应谱特征周期为0.35 s。该桥结构图见图4。图4中，其中Pv为桥墩配箍率，Ps为桥墩纵向配筋率。该桥设防地震烈度为9度，罕遇地震峰值加速度PGA为0.64g，设计地震峰值加速度PGA为0.4g。支座信息见表3。

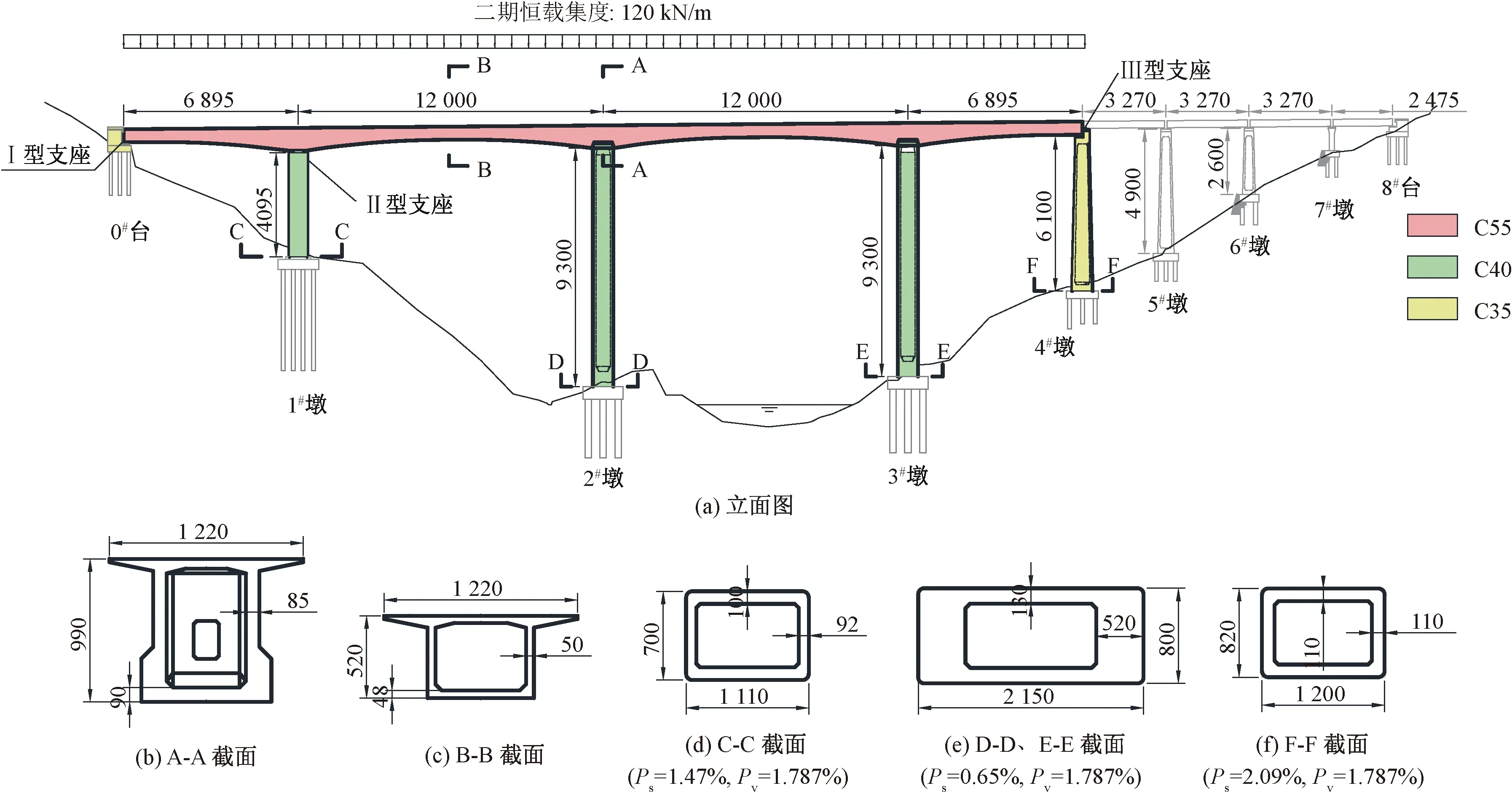
图4 某大跨高墩刚构-连续组合桥结构图(单位：cm)

表3 支座信息

2.2 桥梁有限元模型

桥梁的有限元模型采用OpenSees建立，如图 5所示。其中，主梁采用弹性梁单元模拟；桥墩采用弹塑性纤维梁柱单元模拟；主梁自重和二期恒载等其他附加荷载则作为质量施加在主梁节点上[33]；支座选用理想弹塑性连接单元，其恢复力模型取为双线性模型；伸缩缝采用接触单元模拟。

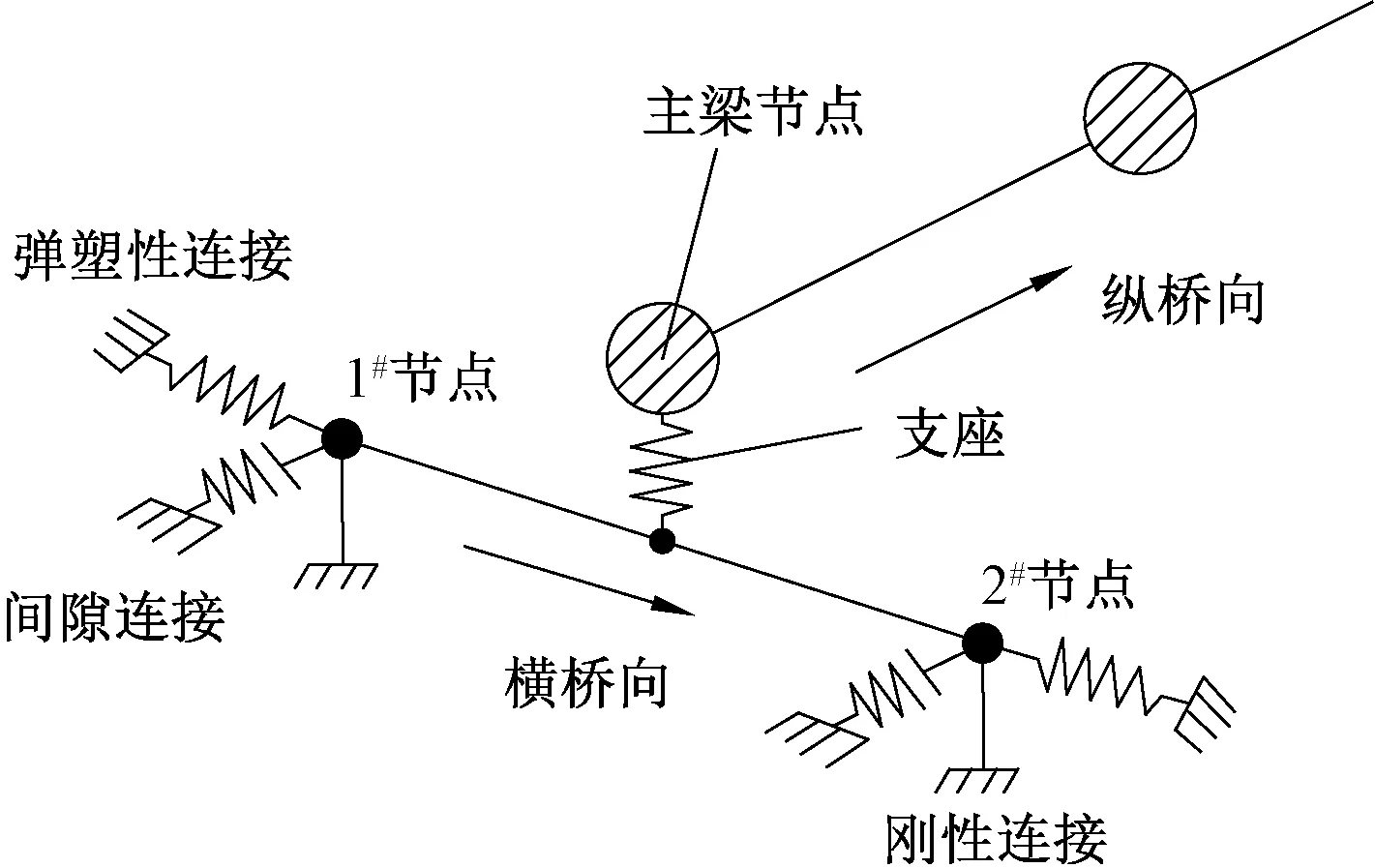
图5 桥台建模示意图

现行规范没有桥台建模与分析的相关规定，为计入桥台对结构地震横、纵响应的影响，依据文献[15]第7.8节建立桥梁结构有限元计算简化模型及局部结构详图见图6。图6中，桥台宽度为1#和2#节点的距离，1#和2#节点与支座底端节点刚性连接，采用文献[15]的有关条文计算得到这两个节点的横、纵向刚度，桥台与主梁间的相互作用采用零长度单元模拟。

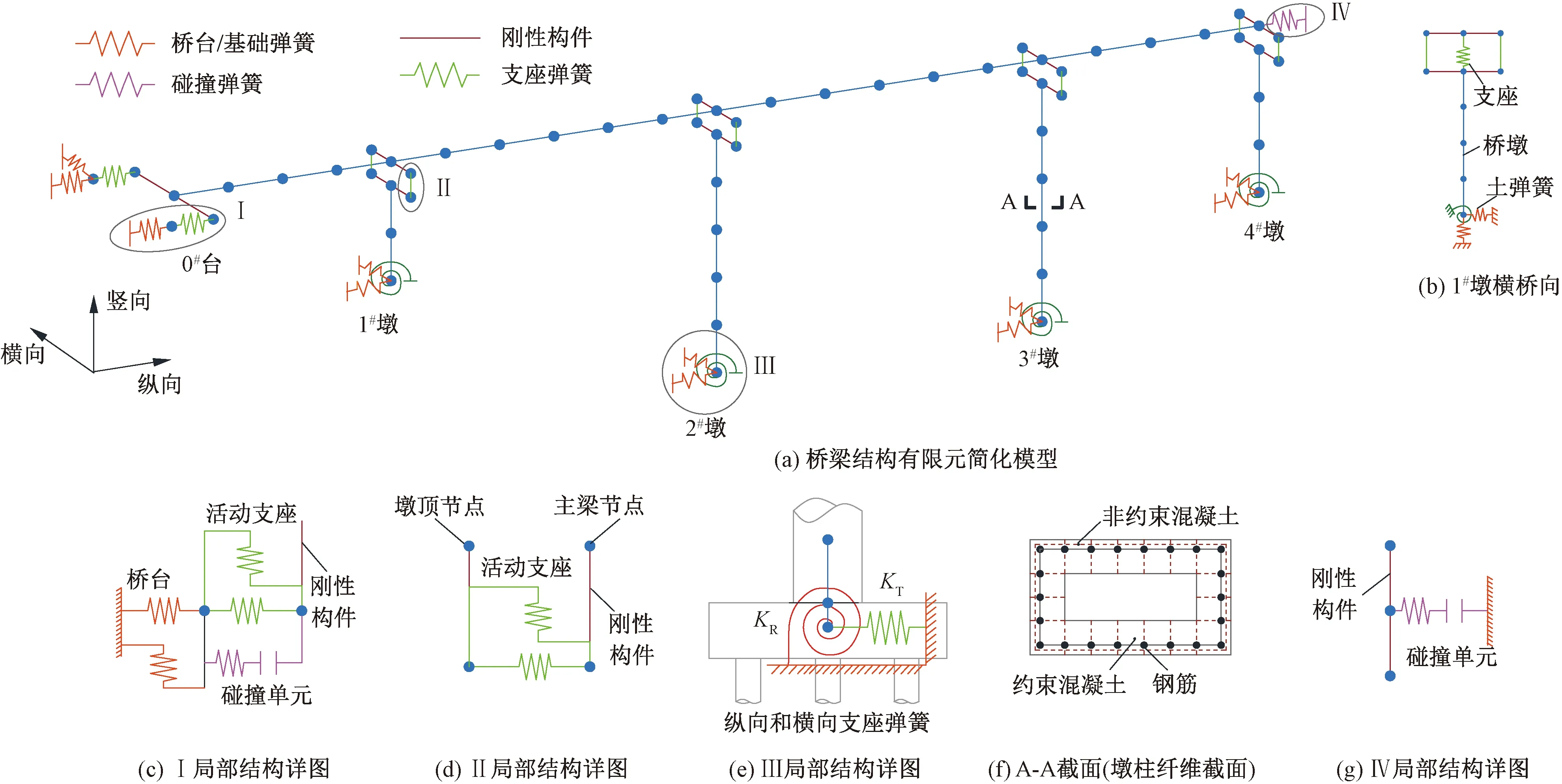
图6 桥梁结构有限元计算简化模型及局部结构详图

桩基础的群桩效应用6个等效弹簧模拟，依据现行规范[34]的相关规定计算其等效刚度值。

2.3 选择地震动

构件三维地震易损性分析的地震动输入选用文献[35]中具有明显脉冲特征的100条近场地震动，其PGA变化范围为0.122 5g～1.079 8g。

由图 7可知，地震动水平输入方向与桥轴线夹角θ(θ=10°×i，i=0,1,…,36)即为地震动水平入射角，其变化范围为0°～360°。当θ=0°时，地震动从0#台至4#墩输入。将θ按10°递增，地震动水平入射角沿逆时针方向旋转，共讨论了37个水平地震动输入对应的桥梁结构地震易损性变化情况，并根据易损性分析结果确定最不利水平地震入射角。

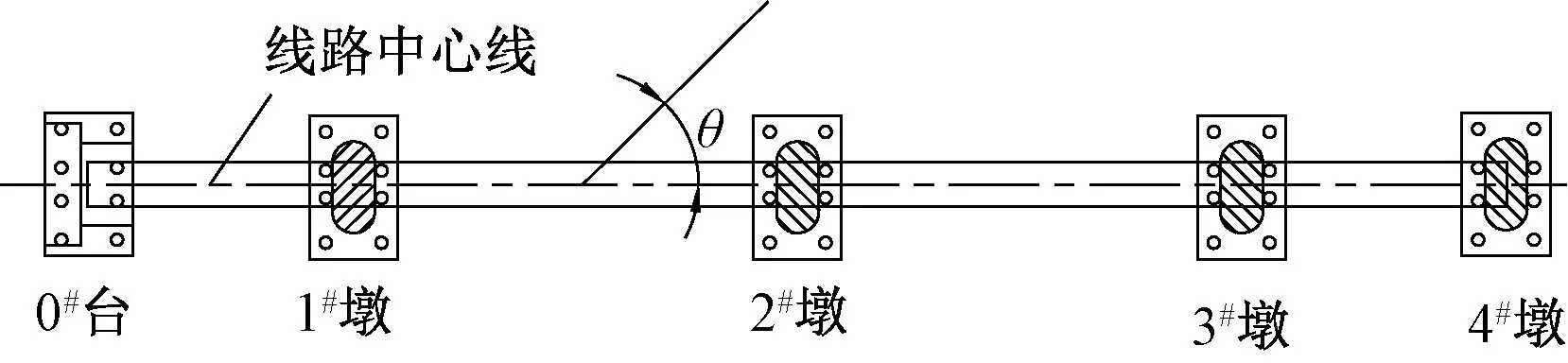
图7 地震动水平入射角示意

2.4 结构参数的不确定

依据高墩大跨刚构-连续组合桥的构造特点，参考结构参数不确定性对结构抗震性能影响的相关研究[36]，确定了如表4所示的结构参数及其分布特征的相关参数。其中：εcu为混凝土极限应变；fc,35为C35混凝土抗压强度，MPa；fc,40为C40混凝土抗压强度，MPa；a为混凝土强度缩放系数；fy为钢筋屈服强度，MPa；b为钢筋应变硬化系数；Es为钢筋弹性模量，GPa；c为二期恒载缩放系数；ρ为混凝土容重，kg/m3；e为支座水平力缩放系数；Nlog为对数正态分布，对应的F1、F2分别为对数均值和对数标准差；N为正态分布，对应的F1、F2分别为均值和标准差；U为均匀分布，对应的F1、F2分别为分布的上、下限。

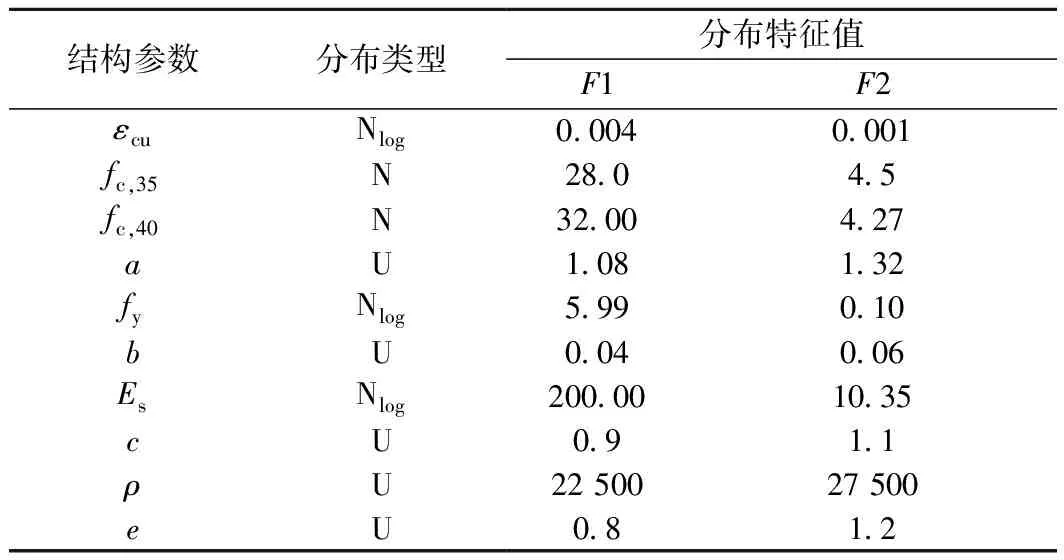
表4 结构参数分布类型及分布特征值

2.5 构件损伤指标

桥梁地震反应分析和震害调查资料显示[10-12]，在横、纵向地震作用下，桥梁主要易损位置包括墩台支座、墩顶截面及墩底截面。

本文采用1.2节的理论，根据背景桥梁的结构特点、配筋情况及及相关规范规定[33-34]，建立各墩柱的剪切和弯曲损伤状态方程，并得到各损伤状态对应的墩柱失效屈服面。限于篇幅，文中仅给出1#墩底截面的弯曲、剪切损伤的判别曲面，如图 8、图 9所示，其他截面的失效屈服面类似。

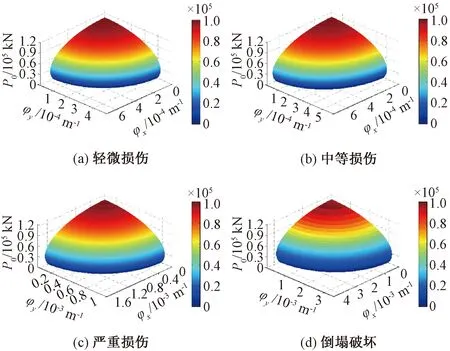
图8 1#桥墩墩底截面4种弯曲损伤状态的损伤判别曲面

图9 1#桥墩墩底截面4种剪切损伤状态对应的损伤判别曲面

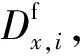
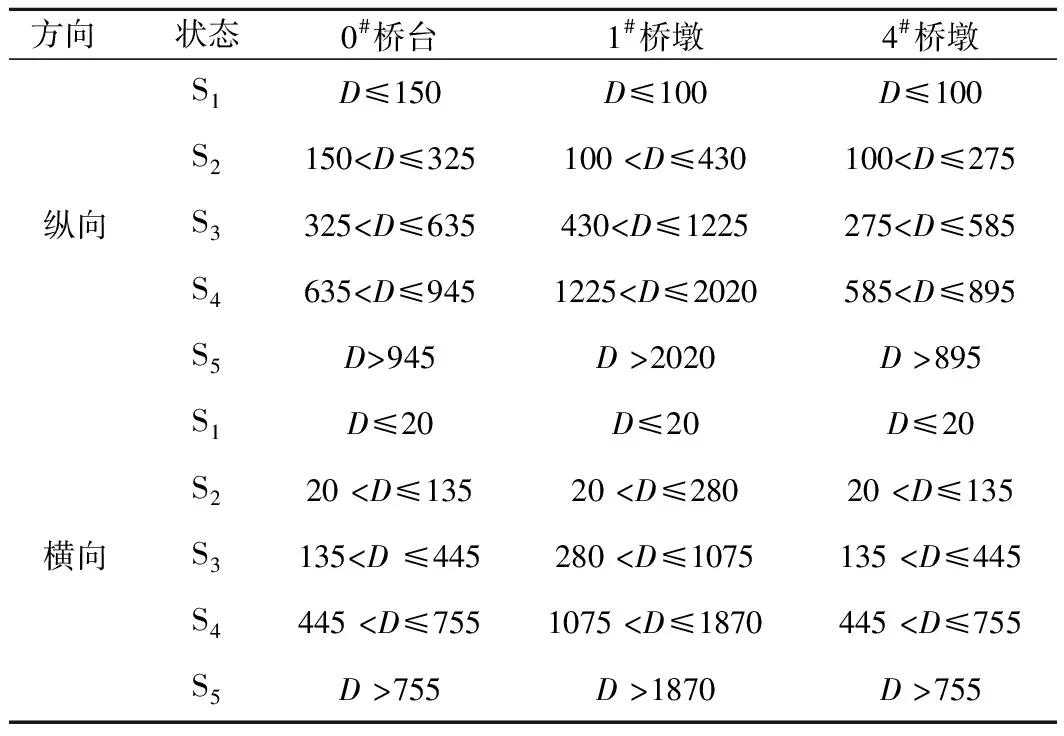
表5 支座损伤指标 mm

2.6 结构三维地震易损性分析

为分析结构的三维地震易损性，水平地震动PGA取为0.1g～1.0g，按0.1g增幅变化；依据GB 50111—2006《铁路工程抗震设计规范》[33]第7.1.4条相关规定，将水平方向PGA强度的65%取为竖向PGA的强度。根据第1节所提方法，按照图 3所示易损性分析流程，先令θ的初值为0°(纵向+竖向地震动输入)，然后依次按10°递增，分别对桥梁结构进行IDA分析，根据各地震动输入方向的分析结果建立桥梁结构地震易损性曲线。最后将各地震动方向对应的地震易损性曲线绘制于同一图中即可形成桥梁结构的三维易损性曲面。限于篇幅，文中仅给出1#～4#墩底截面和各墩台支座在轻微损伤状态下的三维易损性曲面，分别如图 10、图 11所示。

图10 墩底截面轻微损伤状态的弯曲易损性曲面

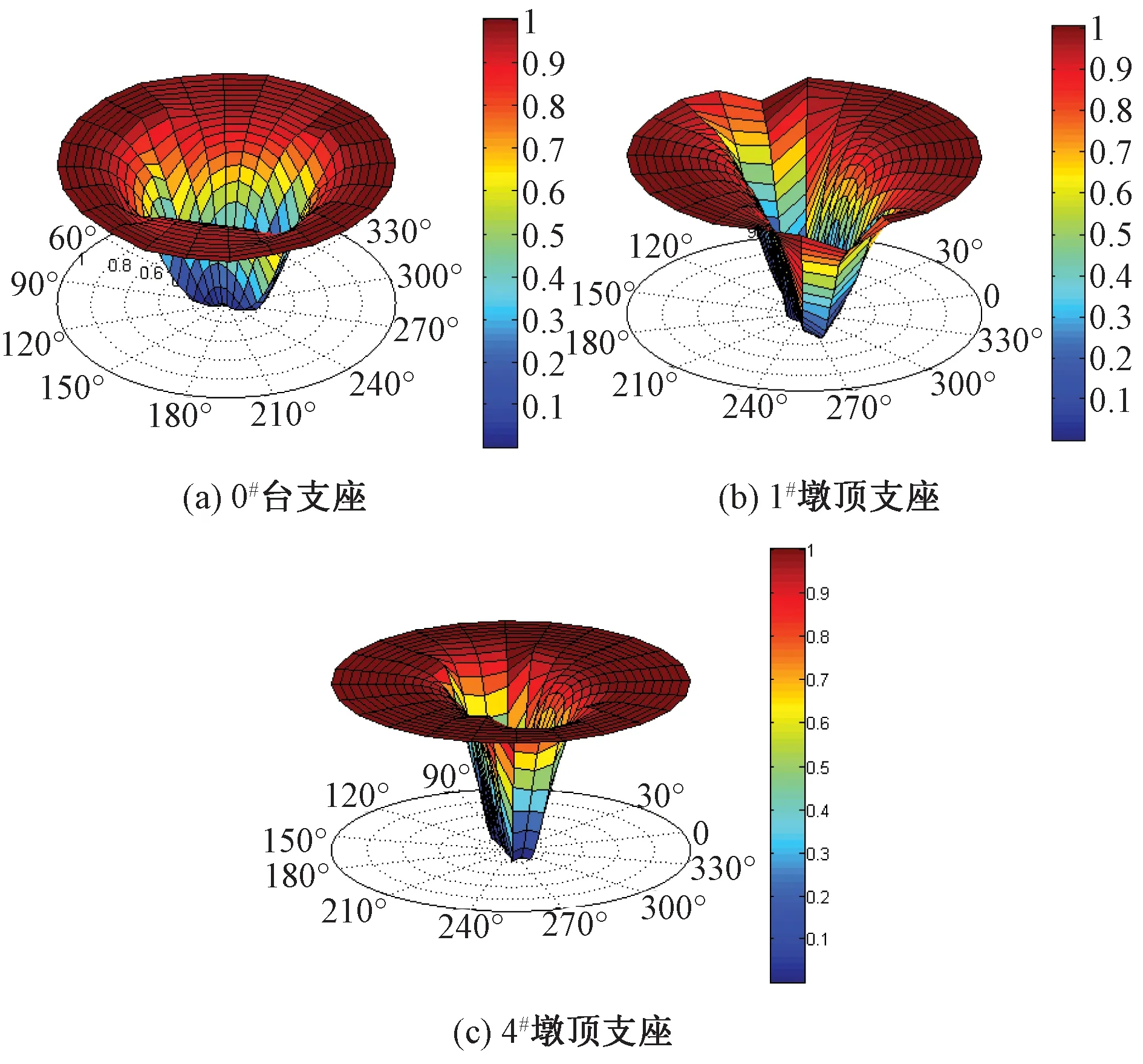
图11 支座轻微损伤状态的易损性曲面

现分别从状态方程和易损性分析结果两方面，验证本文所提方法的正确性。

目前，针对弯曲破坏和剪切破坏两种损伤方式，墩柱地震易损性分析的关注多为墩柱弯曲破坏，关于墩柱发生剪切破坏的易损性分析很少[4]，因此本文仅围绕弯曲损伤开展墩柱状态方程的验证工作，墩柱的损伤指标选为曲率延性比。状态方程和三维易损性分析结果的验证方式为：将式(6)～式(8)仅在顺桥向或横桥向上展开，得到对应的一维状态方程和地震易损性分析结果，并将此结果与基于概率地震需求分析(PSDA)[4]得到的一维(顺桥向或横桥向)地震易损性分析结果进行对比。

墩柱和支座的验证结果如图 12所示，图中包括两种方法计算得到的构件易损性曲线对比图和其损伤概率偏差图。其中，易损性曲线对比图中的位移表示为本文所提的状态方程分析结果，方程为传统易损性分析结果。由图12可知：