雨水入渗下非饱和黏性土路基边坡浅层稳定分析

2021-11-04连继峰张文生谢宏伟

铁道学报 2021年9期

连继峰，罗强，魏明，谢涛，张文生，谢宏伟

(1.西华大学应急学院，四川成都 610039；2.西南交通大学土木工程学院，四川成都 610031)

降雨是导致天然土坡滑动和工程边坡失稳灾害事故频发的最主要和普遍的环境因素。其中，工程边坡与人们交通出行关系密切。降雨诱发的路基突发性病害时常影响列车正常运行，甚至危及行车安全。诸多病害中，以降雨诱发的路基土质边坡浅层失稳最为典型[1]。路基土质边坡浅层失稳与山体滑坡不同，呈现出滑动深度浅、规模小(一般体积仅数方至数百方)，但频率高、分布范围广、突发性强、且易形成灾害链效应等特点[2]，同样给铁路、公路等交通运输带来严重的安全隐患。因此，研究降雨入渗下路基边坡浅层稳定性具有重要工程意义。

李宁等[3]基于非饱和土VG模型与倾斜地表条件下的Mein-larson降雨入渗模型，提出降雨诱发的无限边坡浅层稳定简化分析方法。连继峰等[4]在无限长斜坡稳定计算模型基础上，考虑边坡骨架防护工程力学作用，建立了矩形骨架防护下路基边坡浅层稳定分析方法。覃小华等[5]联合降雨入渗模型与极限平衡法，讨论了基岩面与湿润锋面的稳定安全系数，得到基岩型层状边坡安全系数计算式。马世国等[6]认为地下水下部不透水基岩面和湿润锋面为两个潜在的危险滑面，基于Green-ampt入渗模型建立了考虑强降雨和初始地下水共同作用下边坡的稳定分析模型；Cho等[7]研究了降雨入渗条件下无限长双层边坡的失效过程，建立了双层边坡雨水入渗模型。文献[3-7]的共同点是将降雨入渗模型通过中间参数“雨水入渗深度”与无限长斜坡稳定系数方程联立，进而获得边坡稳定雨强-持时分析方法，然而无限长斜坡稳定分析方法是建立在单位土条式“顺坡平面”失稳模式基础之上，忽视了失稳滑体上下缘抗滑效应，计算结果在长深比较大时是过于保守的[8]。陈善雄等[9]针对具有分层性的膨胀土边坡浅层失稳问题，利用简布法力学原理，考虑降雨入渗边坡内部水分运移空间分布特征，提出以滑体中段为“顺坡平面”，上下缘为折线型的三段组合式失稳模式。詹良通等[10]针对东南沿海山地丘陵地区残坡积土边坡浅层失稳问题，采用Seep/W模块，在边坡初始湿润条件之上施加雨强进行瞬态流分析发现，雨水下渗至残坡积土层底面(差异土层界面)时先发生滞水现象，并逐渐积累产生显著孔压，采用Slide软件[11]中M-P极限平衡法[12]获得了与文献[9]类似的以中段“顺坡平面”为主的三段折线型失稳模式。戴自航等[13]针对有强度差异土层界面边坡，基于单一圆心的隔段圆弧滑动模式，建立了组合滑面的数值积分解法。然而，文献[9-13]计算获得的组合滑面在圆弧-平面相交处均存在滑面不光滑的特征。文献[14]从无限长斜坡土体应力状态出发，提出了强降雨入渗坡体形成饱和渗流下边坡浅层“顺坡曲面”破坏模式，给出了相关边坡稳定系数方程，但该方程较为复杂不易推广，也未能体现雨水入渗引起坡体内孔隙水压力变化对稳定性的影响。文献[15-16]采用有限单元法，分析了无限长斜坡稳定方法的保守性，研究发现，降雨诱发的边坡滑体在长深比较大时的破坏呈现以中段顺坡平面为主导的“顺坡曲面”破坏模式，验证了文献[14]的合理性，但由于有限元数值模拟常以“输参数出结果”的形式呈现，难以掌握其中间迭代计算过程。可见，准确评估雨水入渗下非饱和黏性土路基边坡浅层稳定性的关键在于失稳模式的合理确定。为此，在无限长斜坡“顺坡平面”失稳模式的基础上，建立降雨诱发的黏性土边坡浅层滑体张拉、剪切、挤压三段式组合失稳模式，推导雨水入渗下，考虑水位抬升影响的非饱和黏性土路基边坡浅层稳定分析方法，探讨基质吸力衰减和水位抬升对稳定性的影响，开展算例形式的对比验证分析。研究可为降雨入渗下路基土质边坡浅层失稳模式提供参考。

1 传统土质边坡浅层稳定分析方法

降雨诱发黏性土路基边坡浅层失稳模式的合理确定是建立稳定评估方法的重要前提。为了便于理解后续改进的新方法，以下首先介绍常用的无限长斜坡法[15,17]。

降雨时，雨水入渗于斜坡坡体内形成湿润锋，湿润锋向下运移直至抵达zw深度处，遇不透水基岩面或弱透水的强度差异土层界面时，将在界面上产生滞水现象并逐渐累积水头[10]，随后在水头h高度内产生平行于坡面向下的渗流，即顺坡渗流。对斜坡倾角为α、深度zw内、长度为L2的土条进行力学分析，见图1(a)。水头高度h=zscos2α，其中zs为滑体所在饱和水层深度。因在无限长斜坡假定下土条条间力Pl与Pr大小相等、方向相反，故二者可不用考虑。顺坡渗流下的流网示意图及用于计算水力梯度的测压管水头计算式见图1(b)。深度zs处的孔隙水压力u为

图1 土条受力及渗流流网

u=γwzscos2α

(1)

式中：γw为水的容重。

采用土水合算方法，将长度L2土条(土骨架和孔隙流体(水和气))作为整体进行隔离体受力分析，土条的重量W2为

W2=(γmzm+γsatzs)L2

(2)

式中：zm为滑体所在潮湿土层深度；γm为潮湿容重；γsat为饱和容重。

土条底部总的法向压力为N=W2cosα，有效法向力N′为

N′=W2cosα-uL2/cosα

(3)

由土条抗滑力T与下滑力S之比定义的安全系数Fs1为

(4)

式中：c′、φ′分别为有效黏聚力、有效内摩擦角。

将式(1)～式(3)代入式(4)，可得土条稳定安全系数Fs1表达式[15]为

(5)

式中：γ′为土体浮重度。

若zm=0，zs=zw，则由式(5)得到式(6)，即无限斜坡饱和顺坡渗流下安全系数表达式[17]。分母也可以看成土条长度L2=1时，有效重力下滑分量γ′zwcosαsinα与渗透力γwzwcosαsinα之和，即

(6)

可见，无限长斜坡法稳定安全系数方程式(5)、式(6)与土条长度L2无关，即单位长度土条的安全系数代表了无限长斜坡的稳定性，又因其仅考虑土条顺坡向滑动，故称为单位土条式“顺坡平面”失稳模式。

综上，无限长斜坡法因安全系数解析式较为简单，至今仍被广泛应用于降雨诱发的边坡浅层稳定分析[2-6]。但其关键的假设是“无限长”斜坡，与实际几何边界的路基边坡情况不符，忽略下缘滑体剪出口和上缘滑体切入口的抗滑效应。故在此基础之上，从几何关系出发，进一步考虑滑体端部的影响。

2 路基边坡滑面几何方程及力学条件

2.1 雨水入渗下路基边坡浅层失稳模式

采用与文献[14-16]相同的假定：①强度差异土层界面与坡面平行；②雨水入渗形成的水位浸润线与坡面平行，见图2。

图2 “顺坡曲面”失稳模式及坐标系位置

关于假设条件①的解释：针对路堤土质边坡，一方面，由于施工工程中，边坡浅层土体不易压实，初期便已形成了“浅疏深密”的路堤边坡分层结构特征[18]，另一方面，受后期环境气候反复干湿循环作用，致使边坡浅层土体松散程度逐年增高，与深层密实土体强度之间的差异日趋显著[8]。基于上述两方面原因，导致边坡浅层与深层力学性质存在较大不同，最终形成了一个明显的分界面。针对路堑边坡，假设条件①适用于以下情况：受风化程度控制的岩土层，一般情况下从坡面向内依次为残坡积土、全风化岩、中风化岩、基岩等，且各层产状一致，与坡面近乎平行，不同岩土层强度差异显著[6,10]。研究发现，降雨时残坡积土与全风化岩的分界面是最易发生的滑动面[5,10]。

关于假设条件②的解释：在假设条件①成立基础上，降雨入渗下，雨水在重力和基质吸力水头梯度双重作用下向坡体内运移，因边坡浅层松散土体入渗能力强，雨水持续向坡内入渗直至抵达差异土层界面深度zw时，由于深层密实土体入渗能力弱，水分将在此处产生滞水现象并逐渐累积产生孔隙水压力[10]，随后在较大的水力梯度下，沿该土层界面产生顺坡向渗流，仅少部分水分继续向深层密实土体渗透，强度差异土层界面又称为不(弱)透水界面。故此种情况下，假设条件②也是可取的。

研究表明，降雨导致边坡浅层滑动呈现上缘张拉破坏、下缘挤压破坏和中段剪切滑动模式[1]。考虑单位土条式“顺坡平面”失稳模式的不足，提出路基边坡浅层失稳由上缘张拉区和下缘挤压区为异心圆弧面、中段主滑区为顺坡平面组成的“顺坡曲面”失稳模式，见图2。

2.2 路基边坡典型界面几何方程

为便于求解滑面方程，建立直角坐标系，原点于坡趾A点处。令边坡坡比为1∶n、坡高为H，上下缘滑体滑动圆心分别为o2(xuo，yuo)和o1(xdo，ydo)，下标d和u分别代表下缘和上缘，中段主滑区滑动深度为zw，则可得路基边坡边界方程为

(7)

由假设条件①②可知，浸润线y2方程和强弱差异土层界面y3方程分别为y2=y1-zm和y3=y1-zw。由此，获得三段式组合滑体滑面y4方程式为

(8)

式中：约定xA下标为图2中A点相应横坐标，其余类同。

2.3 “顺坡曲面”组合滑体静力平衡方程

2.3.1 “顺坡曲面”组合滑体受力分析

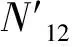
异心式“顺坡曲面”失稳模式与无限长斜坡的“顺坡平面”失稳模式不同，上下缘滑面为两段异心圆弧，以至于滑体底部反力与坐标相关。目前，为了获得整个滑体稳定问题的解答，对土条两侧条间力大小、方向进行的系列假设形成了一整套较为完善的极限平衡法[12]。针对异心式“顺坡曲面”组合滑面，可借鉴上述任意一种对条间力的处理方法。但随着考虑条间力数目的增多，迭代计算过程越趋复杂。

为简化分析，上下缘滑体土条条间力假设同Fellenius法[19]：等值反向，方向与底面平行。同时常用条分法计算精度除了与条间力假设相关外，还受土条划分个数影响。因此，滑体上下缘圆弧滑面处采用微分土条处理，见图4。其中，dW为重力；dN′为土条底部有效法向反力；dN为土条底部法向应力；dT为切向阻力；dUs为土条底部孔隙水压力；h为土体底部中点测压管水头；hm和hs分别为土条潮湿段高度、土条饱和段高度，h=hscos2θ。

边坡浅层以顺坡向下稳定渗流为主导下，采用有效应力法，隔离体受力有两种方式[19]：①将土骨架与孔隙流体(水和气体)作为整体取隔离体，进行受力分析；②土骨架和渗透水流为独立的相互作用的受力体系。两种方式下获得的结果相近[19]，采用方式①，土条底部水压力dUs，通过图4(a)中流线和等势线的关系确定dUs=hγwdl。

Fredlund等[20]提出了基于双应力变量表达的非饱和土抗剪强度式为

τf=c′+(σ-ua)tanφ′+(ua-uw)tanφb

(9)

式中：(σ-ua)为净法向应力；(ua-uw)为基质吸力；φb为第二摩擦角，代表给定(σ-ua)下不同基质吸力所对应的抗剪强度曲线倾角；tanφb为基质吸力对抗剪强度的贡献速率。

同时，也可将式(9)写为

τf=c+(σ-ua)tanφ′

(10)

式中：c为表观黏聚力，c=c′+cs，cs=(ua-uw)tanφb代表吸附强度。

当土体达到饱和状态时，φb=φ′，式(9)退化为基于Terzaghi有效应力原理的抗剪强度式为

τf=c′+(σ-uw)tanφ′

(11)

因此，针对浸润线以上AG段、FE段和以下滑面GF段，安全系数Fs均采用常用的强度储备安全系数定义，可得极限平衡条件方程为

(12)

式中：dl=dx/cosθ；dN′、dN分别为

dN′=dWcosθ-dUs

(13)

dN=dWcosθ

(14)

dW=(hmγm+hsγsat)dx

(15)

其中，

(16)

hs=

(17)

2.3.2 静力平衡方程及安全系数表达式

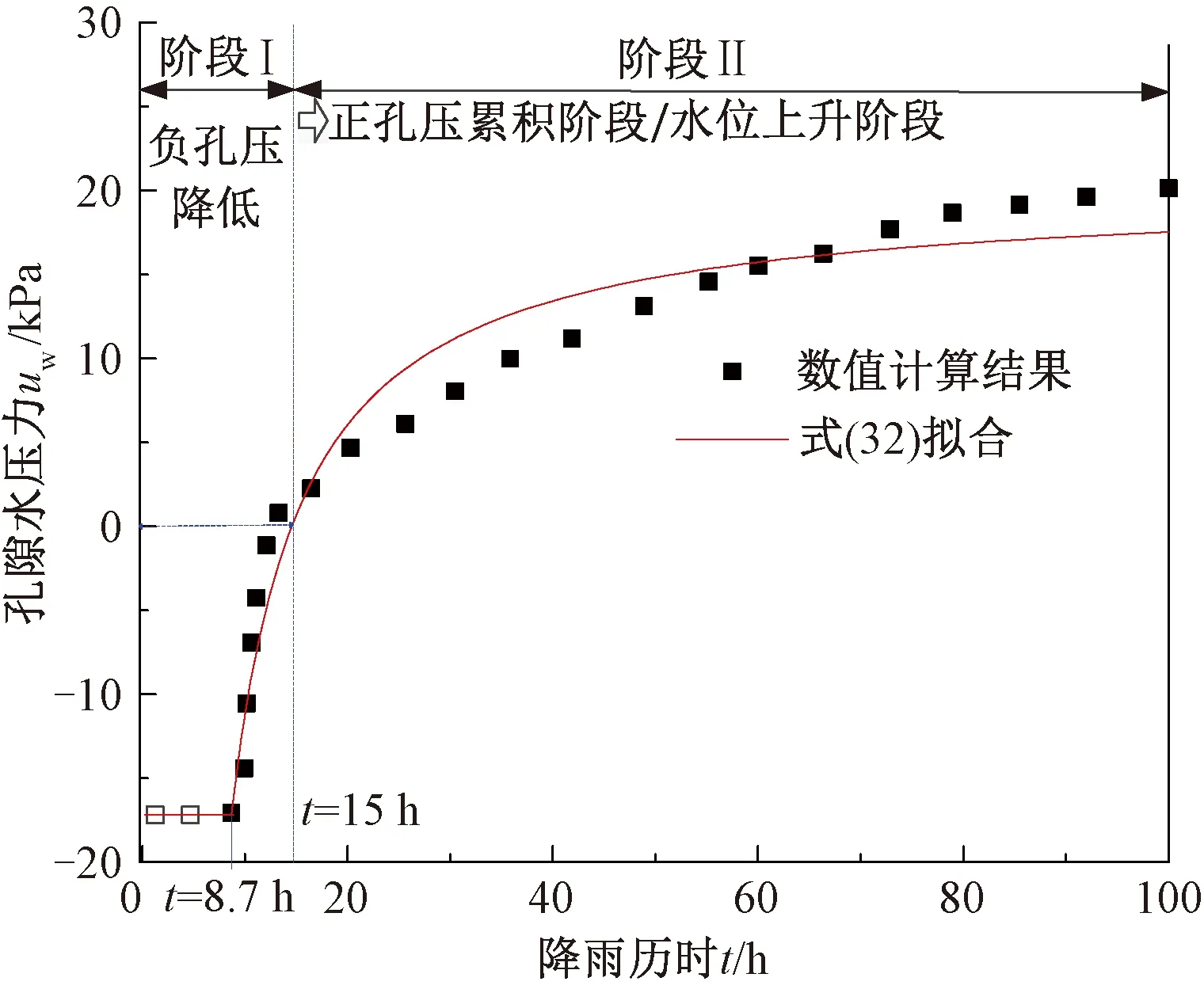
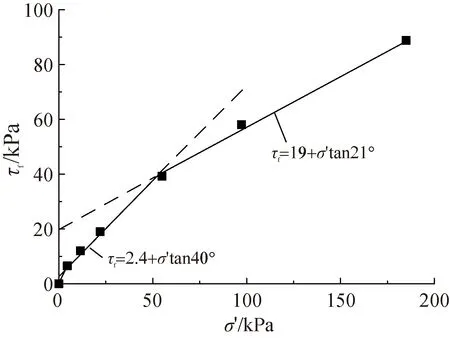
对于一般工况(0

(18)

(19)

式中：R′为Ea或Ep对圆心的力臂。

下缘滑体力矩平衡方程MT3=MS3，其中下滑力矩MS3和抗滑力矩MT3分别为

(20)

(21)

中段主滑区滑体静力平衡方程为

(22)

由式(18)～式(21)可得

(23)

(24)

将式(23)和式(24)代入式(22)中，得出上下缘力矩平衡和中段滑体静力平衡的异心式“顺坡曲面”组合滑面安全系数积分表达式为

Fs=

(25)

式中：M′T1和M′S3按式(26)、式(27)计算(因微分量dx/2较小，可视(x-x0+dx/2)≈(x-x0)。积分区间在(xC,xE)和(xA，xB)内dT和dW按式(12)～式(15)分段求解为

(26)

(27)

当L2减小至零时，假定浸润线以上滑体不考虑基质吸力对抗剪强度的影响即孔压为零，则滑动土体退化为仅由上缘张拉区和下缘挤压区组成的传统整体式“圆弧滑动”失稳模式，式(25)退化为

(28)

式中：MS1+S3=MS1+M′S3；MT1+T3=M′T1+MT3。

当L2增大至无穷大时，滑动土体还原为仅由中段主滑区顺坡平面土条构成的无限长斜坡“顺坡平面”滑动模式，式(25)还原为

(29)

综上可知，式(25)是建立在上下缘为异心圆弧面、中段为顺坡平面组成的“顺坡曲面”失稳模式基础之上，采用双应力变量的非饱和土抗剪强度模型，满足滑体力学平衡条件，属刚体极限平衡法范畴。因此，将其称为非饱和黏性土路基边坡浅层异心式“顺坡曲面”组合滑面法。该方法克服了无限长斜坡稳定分析方法不能考虑滑体上下缘抗滑效应的缺点；当中段滑主滑区长度L2增大至无穷大时，还原为无限长斜坡稳定分析方法，当L2减小至零时，退化为整体圆弧滑面法。

2.4 基于三段组合式滑体的两参数搜索策略

确定路基边坡最危险滑动面圆心坐标及半径是稳定分析中最繁杂的工作。若能依据滑面满足的几何约束条件，确定滑面位置，可有效减少盲目搜索带来的诸多不便。

(1)建立三段组合式滑体参数与滑面圆心关系

在坡长确定情况下，组合式滑体三个参数(L1、L2和L3)中仅有两个自由变量，通过建立上、下缘滑动范围L1和L3两参数与滑面圆心坐标的关系，确定顺坡曲面组合滑面的位置。在保证具有一定精度的条件下简化搜索维数，假设下缘滑面过坡脚，且上下缘圆弧滑面半径相同，即Rd=Ru=R。由图2中可知，下缘圆心o1(xdo,ydo)过坡趾A点即坐标原点，与顺坡平面B点相切，因此，可建立方程式为

(30)

由式(30)可知，8个方程中有10个未知数，只要给定任意两个未知数，方程(30)即可求解，下缘圆弧滑面和上缘圆弧滑面位置便可确定。

(2)搜索策略

Step1确定下缘挤压区起点B。在包含强度差异土层界面与地表平面(x轴)交点位置，沿差异土层界面上下划分n1等分，每一个等分点对应的横坐标即为L3，且满足0

Step2确定上缘张拉区起点C。沿差异土层界面向下划分n2等分，根据每一个等分点对应的横坐标xC便可计算出L3，且满足0

同时，还要满足L1+L3≤L。以Step1确定的下缘挤压区起点作为搜索外循环，以Step2确定的上缘张拉区起点为内循环，共计n1×n2搜索滑面，每次搜索滑面时即可确定三段组合式滑体的三个参数L1、L2和L3，按式(25)计算安全系数Fs。

由此可见，通过调整下缘滑体长度L3和上缘滑体L1，便可获得安全系数系数最低时为危险滑面因此称为组合式滑体的两参数搜索策略。

3 案例分析及方法对比

3.1 案例Ⅰ：以我国东南沿海山地丘陵地区的残坡积土滑坡为例

东南沿海地区年平均降雨量在1 000～2 100 mm，且70%以上的降雨量集中在雨季，是我国台风、暴雨等气象灾害多发区[10]。该区域花岗岩分布十分广泛，边坡岩土层自上而下依次为残坡积土、全风化花岗岩、中风化花岗岩、基岩，各风化层面与坡面近平行，见图5。现场调查显示，滑坡滑动面一般位于残坡积土与全风化花岗岩的交界面处，其深度为2～6 m，属于浅层土质滑坡。

图5 边坡稳定分析概化模型(单位：m)

由于残坡积土与全风化花岗岩渗透系数差异显著，降雨下渗至残坡积土层底部形成滞水，是发生浅层滑坡的诱因。各土层基本性质参数见表1。

表1 各层岩土性质参数[10]

数值模拟结果显示[10]：降雨时，雨水向残坡积土层内逐渐下渗，在尚未达到残坡积土层底部时，底部土体保持负孔压不变，当下渗至4 m深度时，即雨水达到残坡积土层底部，该处土体负孔压迅速趋于0，并且随着降雨持续进行，孔压呈现双曲线型增加的规律，见图6。

图6 残坡积土层孔隙水压力变化及参数拟合

为此，基于数值结果构造分段双曲线，孔压u计算式为

(31)

式中：u0为初始孔隙水压力，kPa；t0为湿润锋抵达土层底部时间，h；a，b为拟合参数，h/kPa、kPa-1。

将u0=-17 kPa、t0=-8.7 h代入式(31)进行拟合,可得参数a=0.183 h/kPa、b=0.027 kPa-1。由图6可知，式(26)可以近似反映降雨入渗下残坡积土层底部孔隙水压力的变化规律。因此，可将降雨入渗下，边坡内孔隙水压力变化分为两个阶段：阶段Ⅰ为负孔隙水压力降低或吸附强度消散；阶段Ⅱ为正孔隙水压力累积或水位抬升。二者先后对边坡稳定性产生影响。由图6可知，雨水下渗时间t≥15 h以后，残坡积土底部水位开始提升，认为整个残坡积土层内负孔压为零；在t<15 h以前，整个残坡积土层内均为负孔压，但土层中负孔压分布变得较为复杂，为简化分析，假定整个残坡积土层内负孔压为底部负孔压的一半。安全系数随降雨历时变化的计算结果见图7。

图7 安全系数与降雨历时关系

由图7可见，阶段Ⅰ即负孔压降低阶段，安全系数可视为线性变化；阶段Ⅱ即正孔压双曲线型升高阶段，安全系数则呈现双曲线型降低的规律。同时，简化解与数值计算获得的安全系数随降雨历时变化的规律基本一致。安全系数量值的少许偏差主要是因为数值解采用Morgenstern-Price严格条分法，所得安全系数与Bishop相近。故相同降雨历时下数值解结果略高于采用瑞典条分法受力模式的“顺坡曲面”组合滑面法。安全系数Fs=1.00时的“顺坡曲面”危险滑面见图8。

图8 边坡Fs=1.00对应的危险滑面(单位：m)

3.2 案例Ⅱ：以美国南加州黏性土边坡失稳为例

美国南加州(Southern California)经历罕见强降雨，致使洛杉矶县(Los Angeles County)发生了数千处边坡失稳，其中绝大多数是浅层溜坍破坏，溜坍体大多处于滑动深度zw=0.5～1.2 m之间的较低应力水平[20]。通过慢剪试验测得了压实系数为0.90的饱和重塑黏性土抗剪强度，见图9。可见在较低压力(5～15 kPa)段的有效黏聚力c′=2.4 kPa、有效内摩擦角φ′=40°，常规中等压力段，即50～200 kPa压力范围c′=19 kPa、φ′ =21°。

图9 土体强度分段线性表示

表2为路基坡高H=6 m、坡比为1∶1.5、入渗深度zw=1.2 m时，边坡浅层稳定安全系数在不同水位抬升高度zs下的计算结果(取潮湿重度γm=17 kN/m3、饱和重度γsat=20 kN/m3)。由表2可见，随zs的增加，Fs也相应降低。若以规范Fs=1.25为限值[21]，水位抬升高度zs>0.7 m后将不满足设计要求，这与暴雨过后现场发生的大量浅层溜坍现象吻合。