基于曲面轮廓投影的道岔区段轮轨多点接触几何计算方法

2021-11-04秦航远刘金朝孙善超

铁道学报 2021年9期

秦航远，刘金朝，孙善超

(中国铁道科学研究院集团有限公司基础设施检测研究所，北京 100081)

轮轨关系是铁路系统重要的接触关系之一，轮轨型面匹配的非线性是造成轮轨系统动力学非线性特征的重要因素[1-4]。在轮轨关系研究领域，主要包括轮轨接触几何状态和轮轨滚动接触力研究两方面。其中，轮轨接触状态直接影响轮轨之间的接触应力，进而影响列车通过时车辆与轨道的动力学响应[5-6]。

轮轨接触几何的计算方法随着轮轨型面外形设计的发展而推进，经历了从锥形踏面和圆弧形钢轨过渡至任意形状型面，从二维空间过渡至三维空间的过程[7]，从单点接触过渡至多点接触的过程[8-10]。在三维轮轨接触几何计算方面，先后有学者提出了迹线法和投影法求解三维空间下的轮轨接触状态[11-12]，并对上述方法的计算结果与商用软件Adams进行了比较[13]。根据轮轨潜在接触线上各点应满足任意相同坐标系下踏面上该点的车轮轮廓线的梯度方向向量与钢轨沿x轴的方向向量相互垂直的原理，有学者提出了三维轮轨潜在接触线在笛卡尔坐标系下的解析表达式[14]。在多点接触的研究方面，有学者考虑轮对横移与摇头的同时，还将侧滚与浮沉考虑为独立的自由度而非横移与摇头的函数，并利用轮廓分区法和迹线法求解轮轨接触几何状态，有效地计算了轮轨的两点接触及非正常一点接触问题[8]；在迹线法求得轮轨接触状态的基础上，有学者通过求解轮轨型面垂向距离的一阶导数和二阶导数，结合轮轨弹性压缩量，研究了在轮轨多点接触的判定以及计算方法[9,15]；在道岔区轮轨接触几何求解方面，软件Nucars给出了一种能够较为精确模拟轮轨接触状态的模型，并对其不断进行改进[16]；另有学者利用数值分析方法得到了道岔纵向任意断面的轮轨接触点分布[17]；之后，有学者提出了考虑铁路道岔转辙器部件轮轨两点接触的计算方法，该方法在传统迹线法求解接触几何参数的基础上，分别求解单侧车轮到尖轨和基本轨的最小距离，通过逻辑判断对转辙器部件处的轮轨多点接触状态进行求解[10]。此外，基于法向切割法，有学者研究了车轮型面的演变对道岔区轮轨接触几何关系的影响[18]。在轮轨接触几何的快速计算方面，有学者在利用多体系统动力学进行车辆耦合系统仿真时，在三维轮轨接触几何计算方面，通过线下的接触几何分析预先获得车轮踏面及轮缘接触点位置变化表，并将其用于三维轮轨的接触几何计算中，该方法同时可考虑轮轨相互脱离的情况[16]。

在轮轨接触几何计算方面，现有方法(如迹线法[11]、投影法[12]等)均假设轮轨刚性接触、且左右侧车轮与钢轨同时接触，导致在轮轨接触状态的迭代求解中，均利用轮轨型面几何关系迭代调整轮对姿态角，而未考虑力学条件，与实际情况有所背离，因此在仿真的迭代过程中会逐步积累计算误差，最终导致计算结果与实际情况有所偏离。此外，由于道岔区段复杂多变的轨道结构状态，一侧车轮与钢轨脱离或两侧车轮同时脱离的情况也可能发生；同时，道岔区段由于轨道结构的变化、车轮踏面的磨耗以及列车运行状态的不稳定，轮轨间多点接触的情况也时有发生[17-20]，而现有方法在计算轮轨表面的相对距离时均采用垂向位移为依据。因此，为了对道岔区段的轮轨滚动接触力进行更为精确的仿真计算，需要建立能够更为准确模拟道岔区段真实轮轨接触关系的轮轨接触几何求解模型。

1 坐标系及其转换关系

三维空间中自由运动的任意刚体均有6个自由度，即沿X、Y、Z轴的平动自由度以及绕X、Y、Z轴的转动自由度，其名称依次为伸缩、横摆、沉浮以及侧滚、点头、摇头。在车辆系统动力学的研究中，针对不同的车辆结构部件和不同的动力学问题，建立不同的参考坐标系对动力学问题进行描述，坐标系示意见图1。

图1 坐标系示意图

全局坐标系oxyz：坐标系原点位于动力学计算时的初始位置的轨道中心线上，x轴沿轨道列车运行方向，z轴竖直向上，y轴按照右手螺旋定则确定。

轮对坐标系oxwywzw：坐标系位于轮对质心位置，xw轴在水平面内沿轮对前进方向，zw轴位于轮对轴线所在铅垂面内且垂直于轮对轴线指向上，yw轴沿轮对轴线方向，按照右手螺旋定则确定。轮对坐标系与全局坐标系之间的变换关系体现了轮对的运动姿态变化，其可以根据全局坐标系分别绕x轴以轮对侧滚角旋转再绕z轴以轮对摇头角旋转得到。

轮轨接触坐标系oxcyczc：坐标系原点位于左右轮对的名义滚动圆与踏面母线交点上，xc轴在水平面内沿轮对前进方向，zc轴位于轮对轴线所在铅垂面内且垂直于轮对轴线指向上，yc轴沿轮对轴线方向，按照右手螺旋定则确定。

全局坐标系oxyz、轮对坐标系oxwywzw以及轮轨接触坐标系oxcyczc的空间关系见图1。其中，轮轨接触坐标系与轮对坐标系各坐标轴方向一致，其差别仅为坐标系原点位置，轮轨接触坐标系原点位于名义滚动接触点处，而轮对坐标系原点位于轮对质心处。因此，轮轨接触坐标系至轮对坐标系的坐标转换关系即为将轮轨接触坐标系中各点z方向坐标减去名义滚动圆半径，同时y方向坐标加/减名义滚动圆间距之半。转换公式为

(1)

其中符号函数定义为

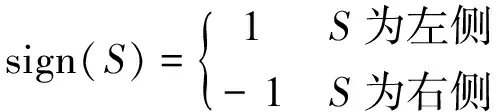
(2)

式中：sign(·)为左右侧车轮逻辑变量，左侧车轮sign(·)取1，右侧车轮取-1；b为名义滚动圆间距。

轮对坐标系与全局坐标系的关系反映了轮对自身的姿态变化，包括轮对相对钢轨的平动以及轮对自身的转动，在轨道-车辆系统中，轮对的转角主要考虑沿全局坐标系x轴转动的侧滚角φ和沿全局坐标系z轴转动的摇头角φ，其中考虑侧滚角φ的坐标变换矩阵为

(3)

考虑摇头角φ的坐标变换矩阵为

(4)

上述两坐标系转换关系为

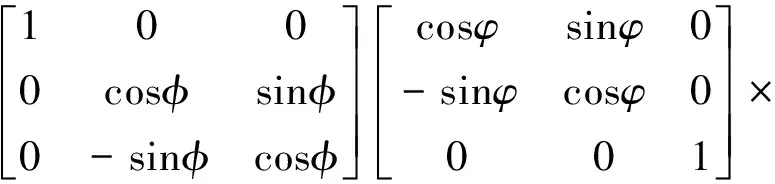
(5)

式中：xcm、ycm、zcm分别为轮对沿全局坐标系各轴的平移分量。

2 基于三维曲面投影的道岔区段轮轨接触几何求解方法

以迹线法、投影法为代表的传统的轮轨接触问题中，轮轨接触几何计算需首先假设轮轨表面刚性接触，且左右侧车轮与钢轨同时发生接触。此假设导致轮对侧滚角与轮对横移量之间存在一定的约束关系，而非两个相互独立自由度，在每个给定横移量下需要迭代求解相应的侧滚角，从而得到当前状态下的轮轨接触几何关系。以上方法无法考虑轮轨瞬时脱离的情况，与真实情况有所偏离，特别是在道岔区段轮轨接触关系相对复杂的工况下。据此，本节提出将轮对横向、垂向平动自由度与侧滚、摇头转动自由度均考虑为独立变量，而某一时刻的轮对姿态完全由前一时刻的轮对动力学方程计算得到。

2.1 三维车轮踏面模型

轮轨接触求解的前提是需要对轮轨的三维型面外形进行准确的建模及边界元的网格划分。根据轮对旋转体的特性，可根据车轮踏面母线及轮对轴线方程对车轮踏面进行建模，其方法如下：

假设轮轨接触坐标系下车轮踏面母线方程为zc=f(yc)，与其上各点坐标为(0，yc，f(yc))，则该处轮径为R0-f(yc)，其中R0为轮对名义滚动圆半径，根据旋转体特性，轮轨接触坐标系下车轮表面某点(xc，yc，zc)应满足关系为

xc2+(R0-zc)2=[R0-f(yc)]2

(6)

在已知踏面网格点坐标(xc，yc)下求得对应的zc数值，从而实现车轮踏面的三维建模。将轮轨接触坐标系下的车轮上各点经式(1)和式(5)依次转换至轮对坐标系及全局坐标系，从而完成全局坐标系下车轮踏面的三维数值建模。

轮轨滚动接触力的大小与轮轨型面的法向渗透量相关，同时轮轨接触力的方向需要根据车轮踏面各个节点处的外法线方向进行确定。因此，在对车轮表面进行三维数值建模之后，还需要通过几何关系求解得到踏面上各个节点处的外法线方向向量。在轮轨接触坐标系下，根据两互相垂直直线的斜率乘积为-1的特性，可以得到轮轨接触坐标系下车轮踏面与横切面(oyz平面)交线在横坐标yt处的法线方向向量为

(7)

设由轮对轴线指向轮对踏面外侧为外法线方向向量正方向，同样依靠旋转体的特性，车轮踏面在y=yt横切面(即oxz平面)内各点处的外法线方向可以通过坐标变换的方式求得，该点外法线方向向量为

Vnw=AθVn0

(8)

式中：Aθ为坐标变换矩阵。

(9)

其中，θ=arcsin(x/R)

与踏面节点坐标的空间转换关系相同，踏面外法线方向向量由轮对坐标系转至全局坐标系的坐标变换式为

Vn=AφAφVnw

(10)

2.2 道岔区钢轨模型

与直线区段不同，道岔区段的钢轨廓形随列车行进方向而变化，通常对岔区钢轨廓形的建模方式为：首先对岔区各关键截面钢轨廓形进行离散，之后插值生成各个截面处的钢轨表面廓形。

以12#道岔为例，12#可动心轨单开道岔的曲尖轨共有7个关键截面，分别对应尖轨顶宽为尖端(两处)、3、20、35、50、71 mm。而辙叉区长心轨关键截面共有5个，分别对应长心轨尖端、顶宽13、20、40、71 mm截面。

在关键截面廓形生成的基础上，将各个关键截面之间的钢轨廓形进行线性插值，假设全局坐标系下两个相邻关键截面上相对应的点的坐标分别为(x1，y1，z1)和(x2，y2，z2)，则以上两截面之间的x方向坐标为x0处的廓形对应点为

(11)

综上，通过对关键截面处钢轨廓形的数值建模，并通过插值生成各个关键截面之间各处钢轨廓形，可以获得道岔区段的连续钢轨廓形三维数值模型。为列车通过岔区时的轮轨关系随时间变化的分析计算提供模型依据。

2.3 三维轮轨接触几何计算方法

2.3.1 三维轮轨接触几何计算流程

在所建立的三维车轮踏面数值模型基础上，求解模型中各个节点沿该点外法线方向向量到钢轨廓形的距离，作为轮轨接触力求解的前提。然而，由于模型节点数量众多，而真实接触斑面积很小，逐点依次求解会造成计算资源的大量浪费，大大降低了计算效率。因此，基于轮轨潜在接触线首先求得可能接触斑区域，并根据当前轮对所在位置对应的钢轨廓形截面是否发生改变选取对应算法对三维空间下的轮轨接触几何进行求解，计算流程见图2。

图2 三维轮轨接触几何计算流程

轮轨接触几何状态由当前时刻轮对的运动姿态所确定，即轮对沿x、y、z三个方向的平动以及侧滚角φ和摇头角φ。根据以上轮对初始运动状态计算轮轨的潜在接触线，并计算潜在接触线上各个节点与钢轨的法向距离，之后将法向距离小于或等于零的点周围区域作为潜在接触区，最后通过计算潜在接触区内各个节点的轮轨法向距离确定实际接触斑内各个节点的接触几何状态。各部分详细算法在以下各小节中分别给出。

2.3.2 三维轮轨潜在接触线数学模型

车轮踏面的潜在接触线为车轮踏面被沿全局坐标系Y轴的各处横截面(即oxz平面)所截截面最低点的集合。当轮对无摇头角时，轮轨潜在接触线即为踏面母线；当存在一定摇头角时，轮轨潜在接触线则不再位于同一平面内，而成为一条空间曲线。轮对存在一定摇头角及侧滚角时的轮轨潜在接触线见图3。

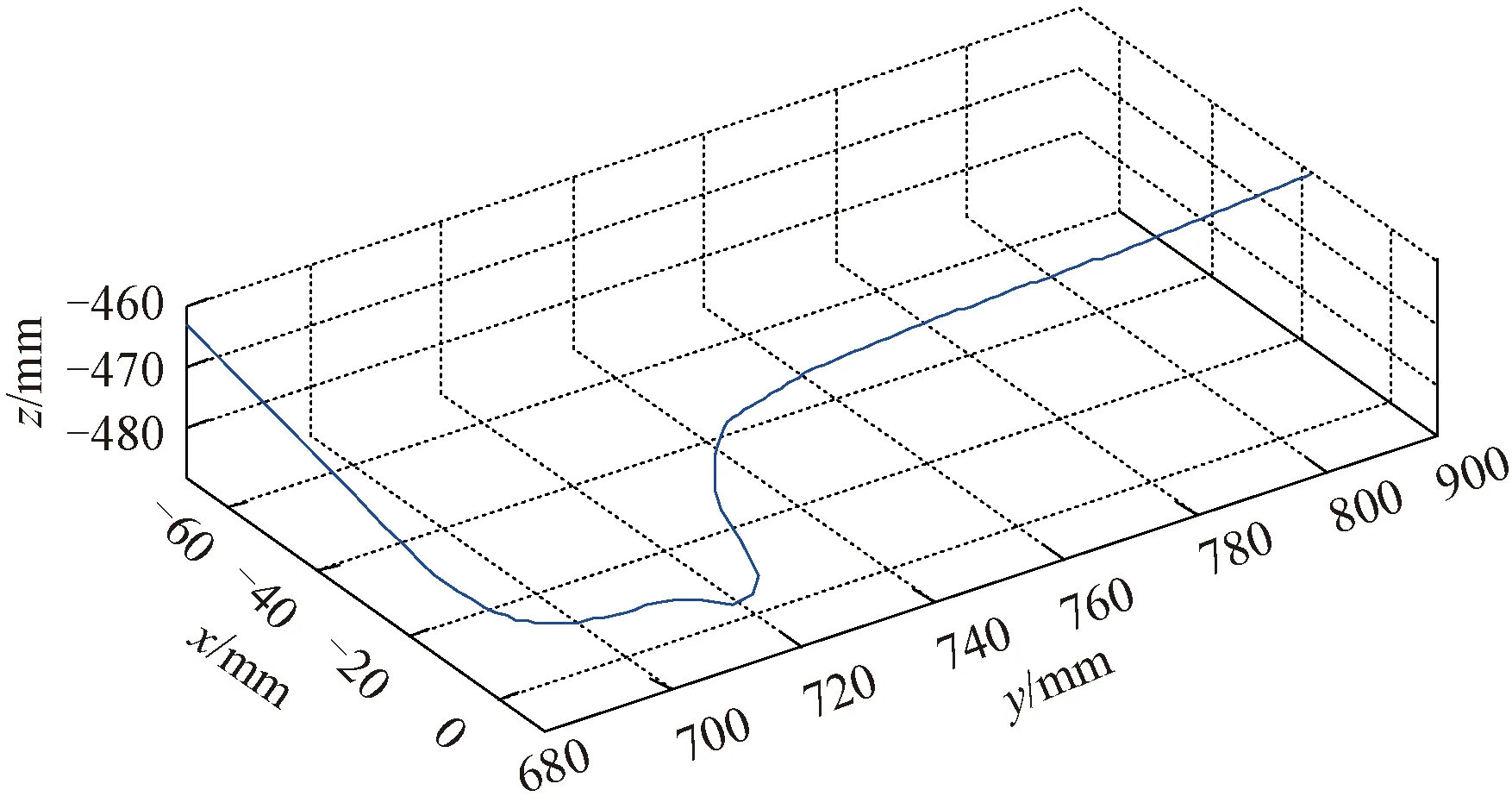
图3 一定摇头角下的轮轨潜在接触线

根据轮轨接触几何约束条件，即车轮踏面与钢轨廓形接触点处的曲线斜率一致，轮轨潜在接触线上各点应满足：任意相同坐标系下踏面上该点的车轮轮廓线的梯度方向向量与钢轨沿X轴的方向向量相互垂直，表示为

Gr·Ωrxy=0

(12)

式中：Gr为轮对坐标系下车轮轮廓线的梯度方向向量；Ωrxy为钢轨延伸方向向量在轮对坐标系下的x、y轴坐标表示，即

(13)

(14)

假设轮对侧滚角φ较小，认为cosφ=1，sinφ=φ，因此可将式(14)写为

(15)

因此有

(16)

代入式(12)，可得

(17)

式(17)中，z方向坐标可以表示为轮对坐标系下xw、yw的函数，即z=fw(xw，yw)，因此可根据式(17)计算得到轮对坐标系下xw与yw的函数关系，即xw=fwx(yw)，并代入式(5)，可得全局坐标系下轮轨潜在接触线坐标与轮对坐标系下踏面横坐标yw的函数关系为[14]

(18)

2.3.3 直线区段轮轨接触几何计算

假设钢轨沿x轴方向廓形不发生改变，则三维踏面上各点与钢轨廓形的法向距离可以简化为二维问题，利用二维平面内的车轮踏面与钢轨廓形法向距离通过三角函数计算得到。具体为计算车轮踏面上某点沿该点处外法线方向向量Vn在yz平面的分量Vnyz到二维踏面曲线的距离，除以外法线Vn与oyz平面的夹角的余弦所得到，详细计算步骤如下：

Step1确定踏面上某点在oyz平面的坐标(y0，z0)及该点处外法线方向向量在oyz平面的分量(Vy，Vz)，从而确定该点外法线的直线方程为

(19)

Step2求该直线方程与全局坐标系下钢轨廓形曲线方程zr=f(yr)的交点，得到交点坐标(yr，zr)。其中，对于标准廓形而言，可将廓形曲线写为由多段圆弧组成的分段函数，交点坐标根据解析表达式求得，对于非标准廓形而言，交点坐标则需通过拟合及插值方法得到。

Step3计算Step2所求得交点(yr，zr)与踏面上所求点在oyz平面的坐标(y0，z0)的距离为

(20)

Step4根据二维平面内的法向距离hyz与外法线Vn与oyz平面的夹角的余弦cos(θv)，即可求得三维空间下踏面上该点沿法向与钢轨表面的距离为

(21)

2.3.4 道岔区段轮轨接触几何计算

道岔区段由于尖轨、心轨以及导曲线等特殊部件的存在，而使钢轨廓形沿钢轨x轴方向发生变化，无法使用直线区段的轮轨接触几何计算方法。因此，针对道岔区段变钢轨截面的轮轨接触几何计算问题，采用基于数值迭代的方法求解全局坐标系下踏面上任意一点(x0，y0，z0)沿外法线方向向量Vn到钢轨截面的法向位移，详细算法步骤如下：

Step1根据踏面上节点坐标(x0，y0，z0)及该点处的外法线方向向量Vn，计算该点与法向量的mi倍之和，当i=1时，mi=1，则有

(22)

Step2找出全局坐标系沿x方向与xi距离小于阈值的对应钢轨廓形截面，记该截面廓形函数为zr=fi(yr)。

Step3计算该节点(x0，y0，z0)在oyz平面的投影点(y0，z0)沿Vn在oyz平面的分量(vy，vz)T与廓形函数zr=fi(yr)的交点坐标(yr，zr)，所用方法与上一小节一致。

Step4计算交点(yr,zr)与Step1所求得的节点坐标(xi，yi，zi)在oyz平面投影(yi，zi)的距离li，以及向量(yr-yi，zr-zi)与向量(vy，vz)的夹角余弦cosθv。

(23)

(24)

Step5若li小于所设阈值，则踏面上该点与钢轨廓形的法向距离h为miVn的模，符号则与系数mi符号一致。当距离为正时表示踏面上该点与钢轨廓形未发生接触，非正时则说明踏面上该点与钢轨廓形发生接触或相互渗透。反之，若li大于阈值，则根据所求得距离li计算其与向量mi(Vy，Vz)的模的比值，作为系数mi的修正量ni，对mi进行进一步修正。

(25)

Step6根据ni对mi进行修正，得到第i+1步的mi+1。

mi+1=mi[1+sign(cosθv)×ni]

(26)

Step7根据修正后的mi+1返回Step1，依据上述步骤求解新的li+1，直到li+1小于所设阈值时则输出对应h作为该点与钢轨廓形的法向距离。

3 算例分析

本节以实际车轮踏面和正线及道岔区钢轨廓形为参考，利用所提出方法建立三维车轮钢轨型面模型，对其轮轨接触几何状态进行计算求解，本节算例均通过Matlab软件编写并实现。

3.1 三维轮轨型面建模

利用所提出的轮轨接触几何计算方法对三维空间的车轮进行数值建模，踏面及正线区段钢轨外形轮廓见图4。其中踏面型号为LMA型，正线区段廓形为60N，踏面及廓形均建立在轮轨接触坐标系下，钢轨的轨底坡为1/40。

图4 踏面及廓形外形

以车轮为旋转体为依据，建立车轮的三维模型，并计算模型中各个节点处的踏面外法线方向向量，结果见图5。由于实际轮轨接触区域只存在于车轮最下方部分区域，因此为了减少计算量并提高计算效率，车轮的三维模型仅需要建立车轮下方部分节点即可。同理，正线区段钢轨也仅需建立轮轨接触区域附近一段钢轨的三维模型。

图5 车轮三维建模

针对道岔部分钢轨的建模，以12#提速道岔为研究对象，根据尖轨、心轨等区段各个关键截面廓形平面数据，建立上述区段的道岔钢轨三维模型。其中转辙区直向过岔时曲尖轨与直尖轨外形轮廓见图6，其中廓形轮廓共包含7个关键截面，按照尖轨顶宽分别为尖端(a，b)、顶宽3、20、35、50、71 mm，该区段全长19.314 m。

图6 直尖轨与曲基本轨区段关节截面

道岔区段钢轨的三维模型建立，根据各个关键截面的钢轨廓形二维数据，对该区段各个位置的钢轨廓形进行线性插值。其中道岔区段尖轨、心轨等廓形发生变化区段的完整钢轨三维模型根据该区段各个关键截面的廓形数据统一建立，而在实际计算中仅需截取轮轨接触区域附近的一段钢轨廓形。同时，为了保证正线及道岔的交接区段轮轨接触计算的连续性，在道岔变截面区段前后均根据正线钢轨廓形数据插值生成一段正线钢轨三维模型。在转辙区内所截取的直向过岔时直尖轨与曲基本轨部分区段的车轮道岔三维模型，其中网格尺寸为1 mm×1 mm，见图7。

图7 直尖轨与曲基本轨区段轮轨三维模型

3.2 轮轨接触几何计算

以LMA型车轮踏面为研究对象，对车轮在不同姿态下的轮轨接触几何状态进行计算分析。首先对不同姿态下的三维轮轨潜在接触线进行求解，其中在摇头角φ分别等于0°和1°时的三维轮轨潜在接触线分别见图8中黄色实线所示。

图8 不同摇头角下轮轨潜在接触线

可以看出，当轮对摇头角φ等于0°时，轮轨潜在接触线即为车轮踏面母线，而当存在一不为0°的摇头角时，轮轨潜在接触线变为一空间曲线。

通过对轮轨潜在接触线上的各个节点求解空间轮轨接触几何状态，判断其是否与钢轨发生接触，初步对可能的轮轨接触区域进行划分，可省去非接触区域内各个节点的轮轨接触几何状态求解工作，从而大大降低计算量，提高求解效率。在本算例中，所建立的车轮踏面节点个数为53 935，所求得轮轨潜在接触线节点个数为136，仅占总网格数的0.25%。

对潜在接触线上的各个节点求解其轮轨接触几何状态，按照各节点的空间坐标计算其沿踏面在该点处的外法线方向向量在钢轨廓形上的投影点坐标，并以此求得该节点到钢轨的法向距离。轮对沿直向通过12#道岔过程中运动至转辙区直尖轨与曲基本轨某截面时的轮轨接触几何求解过程见图9。对踏面潜在接触线上各节点的计算结果见图9(a)，某节点计算过程的局部放大见图9(b)。图9中红色星号为潜在接触线上节点在全局坐标系oxyz中oyz平面的位置(y0，z0)，绿色箭头指向为该点上的踏面外法线方向在oyz平面的投影(vy，vz)，粉色星号为过该点沿外法线方向向量的直线与所截钢轨断面廓形曲线的交点(yr，zr)，黑色星号为该点沿初始1倍外法线方向向量Vn平移得到的新节点在oyz平面的位置(y1，z1)，黑色圆圈为向量系数经一次修正后所求得新节点位置(y2，z2)，黑色加号为向量系数经二次修正后所求得新节点位置(y3，z3)(图9中未出现)。可以看出，在此算例中，经过一次修正，潜在接触线上各节点沿该点踏面外法线方向在钢轨表面的投影均准确求得，体现出本文所提出方法在计算过程中的高效性及准确性。

图9 道岔区段轮轨表面法向距离计算

以在某一姿态下的车轮踏面分别于正线区段钢轨廓形以及道岔区段某断面钢轨廓形为例，验证本文所提出的三维轮轨接触几何计算方法的计算效果。

轮对在沿全局坐标系y轴横移为-1 mm(即向左平移)，绕z轴摇头角为1°时的正线区段左侧轮轨接触状态见图10。图10中阴影区为由于踏面与廓形两个曲面发生重叠所导致，即为轮轨接触区。

图10 正线区段轮轨接触状态

上述状态下根据前述方法求得的轮轨接触斑内的各个节点与钢轨表面的法向距离见图11。由图11可知，深红色区域为非接触区，接触斑形状呈类似椭圆形，接触斑内轮轨相互渗透量中心区域最大，颜色对应为深蓝色，周围区域逐渐减小，颜色逐步变为红色。可以看出，在正线区段，当轮对摇头角及横移量均较小时，轮轨接触状态为单点接触，接触斑形状接近椭圆形。

图11 正线区段轮轨表面相互渗透区域

轮对在沿全局坐标系y轴横移为-6 mm(即向左平移)，绕x轴侧滚角为0.05°，绕z轴摇头角为3°时在直向通过12#道岔转辙区时，左侧车轮与道岔直尖轨与曲基本轨的接触状态，见图12。图12中阴影区为由于踏面与廓形两个曲面发生重叠所导致，即为轮轨接触区。可以明显看出图12中存在三处阴影区域，分别为踏面与曲基本轨接触区、与直尖轨接触区，以及由于轮对摇头角所导致的部分轮缘与直基本轨侧面的接触区。

图12 道岔直基本轨与曲尖轨区段轮轨接触状态(三点接触)

上述状态下求得的轮轨接触斑内的各个节点与钢轨表面的法向距离见图13。由图13可知，车轮与曲基本轨接触斑形状呈类似椭圆形，而与直尖轨接触斑形状呈类似细长的瘦椭圆形。同时，轮缘与直尖轨侧面接触斑呈带状，这主要是由于此区段直尖轨的廓形所致。可以看出，相比于正线区段，道岔区段(特别是尖轨与心轨等变截面区段)的轮轨接触状态较为复杂。当存在一定的轮对侧滚角、摇头角及横移量时，轮轨接触状态为多点接触，接触斑呈较不规则形状。