陡峭山坡风场数值模拟方法研究

郑德乾 ， 李 亮， 方平治， 马文勇

(1.河南工业大学 土木建筑学院，郑州 450001；2.中再巨灾风险管理股份有限公司，重庆 400000；3.石家庄铁道大学 土木工程学院，石家庄 050043)

1 引 言

与平坦地形风场不同，山地地形风场因受地形起伏的影响，流动更复杂，通常伴随着撞击、回流、环绕和漩涡脱落等现象，使得山地地形的风速预测变得更加困难。

国内外关于山地风场加速效应大都从典型山地模型开始，采用理论分析、风洞试验和数值模拟等方法进行了较为广泛的研究。理论研究方面，以典型山地模型为对象，文献[1,2]较早通过理论模型研究，提出了一种适用于坡度小于20°的山坡的加速效应解析式。Rokenes[3]理论研究了不同地形的加速效应。在风洞试验方面，Kondo等[4]以典型二维山坡为研究对象，分别给出了二维山坡上下游的风速模型，以及不同坡度下二维山坡各个位置处的地形风场加速效应；文献[5,6]则利用风洞试验分别研究了典型山地的湍流强度和加速效应。

与其他方法相比，CFD(Computational fluid dynamics)数值模拟[7-9]具有便于参数分析和拓展工况的优点。Lun等[10]在Kondo[4]的风洞试验基础上，结合各国规范，对不同坡度的典型二维山地地形风场的地形加速效应进行了模拟。方平治等[11]通过数值模拟研究了不同坡度的二维地形风场，并标定了适用于二维地形的数值模拟湍流边界条件。文献[12，13]通过大涡模拟研究了二维和三维地形的平均风和脉动风场特性。对于典型山地风场，山顶处的风速加速效应最为明显，然而文献[10,11]在山顶处的模拟精度不够，此外，已有的数值模拟研究已经考虑了来流边界条件[11]和计算域[14]的影响，但数值计算中如网格尺度、湍流模型以及山顶附近局部处理等也对计算结果有较大的影响，尤其是坡顶局部区域的模拟精度有待进一步提高。

本文以坡角为45°的陡峭山坡为对象，研究了网格分辨率和湍流模型对风场模拟结果的影响；针对山顶局部区域模拟精度较低的问题，详细研究了局部光滑曲线形式，以及光滑过渡段水平长度对数值模拟精度的影响，确定了最优光滑曲线及参数，将数值模拟结果与文献试验和各国规范进行了对比，探讨数值模拟方法的准确性。

2 CFD建模参数设置

本文的研究对象是陡峭山坡，坡角为45°，模型坡顶表面长度设置为7L1，与地表的过渡坡度角为30°，其他参数设置如图1所示，图中C,A,M,B和D为模型迎风面速度和压力监测点。文献[11]对该模型在石家庄铁道大学STDU-1风洞实验室低速试验段进行了测压和测速试验，并进行了数值模拟研究，分析了不同坡度的影响，其中数值模拟所得15°和30°时的小坡度结果与风洞试验的吻合性较好，而45°陡峭山坡则在坡顶分离处与试验值存在一定偏差，因此，本文主要选取45°陡峭山坡为对象，重点解决顶部分离导致的模拟精度问题，相应方法同样适用于坡度较小的山坡。

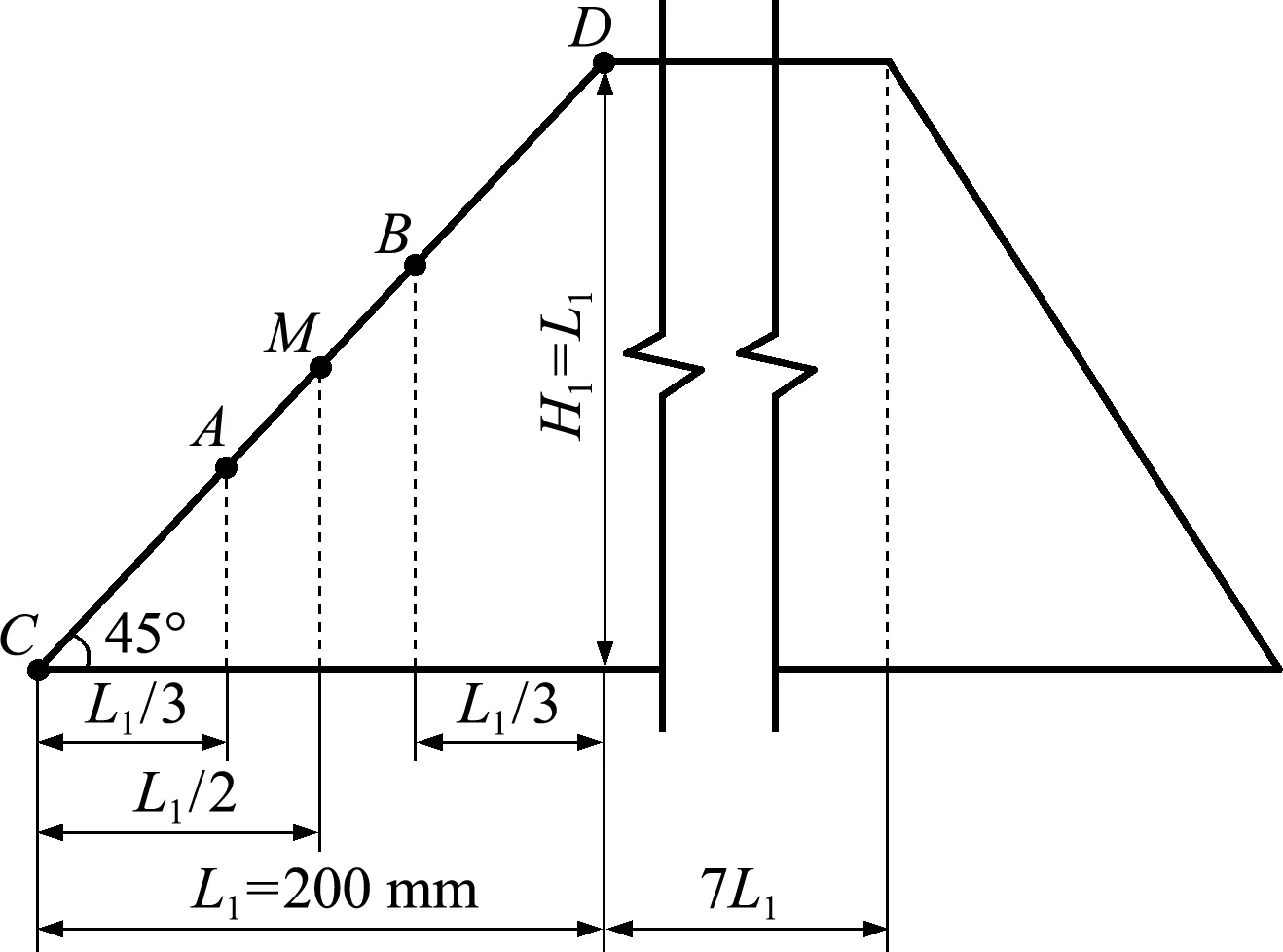
图1 简化模型

数值模拟采用准三维计算域，计算域大小为24000(x)×4000(y)×3000(z)，网格剖分基于分块技术，采用非均匀结构化网格对计算域进行离散，在地面关心区域进行网格加密，详细网格参数列入表1，计算域及网格划分如图2所示。与文献[11]不同，本文详细考虑了网格分辨率、湍流模型、坡顶局部过渡光滑曲线形式以及光滑过渡段水平长度等影响，讨论数值模拟方法的适用性。

表1 网格分辨率

图2 网格划分

入流面采用速度入口，出流面为压力出口，计算域两侧和顶部为对称边界条件，山坡表面及地面为壁面。控制方程的对流采用二阶迎风格式，计算收敛残差取5×10-4。风剖面由风洞试验拟合(图3)得到，其表达式为

(1)

式中u*和z0分别为壁面摩擦速度和地面粗糙度，由图3的试验剖面[11]拟合得出，拟合值分别为0.3752 m/s 和1.5538×10-4m，κ为卡门常数，取 0.42。

图3 平均风廓线比较

在模型表面的关心区域设置与风洞试验相同的5个位置的速度和压力监测点，位置如图1所示，其中近地面处速度监测点在0.01L1～0.11L1高度范围内加密。本文平均风压系数CP,mean和流向风速比Ri x均采用文献[11]试验中梯度风高度(zg=600 mm)处来流平均风速进行无量纲处理。

3 网格分辨率及湍流模型的影响

首先，采用Realizablek-ε湍流模型，对表1所示4种网格工况进行数值模拟，考察网格分辨率的影响。图4为流向风速比、风压系数与风洞试验结果的对比，可以看出，整体上，流向风速比随距离地面位置的增高而增大，在分离点D处达到最大，数值大于1.0，表明存在明显的地形加速效应；平均风压系数随测点距离地面高度的增加不断减小，在分离点D处达到最小且为负压，与风洞试验趋势一致。网格分辨率对流向风速比和风压系数的影响均不甚明显，进一步加密网格后数值模拟精度未见显著提高。综合数值模拟精度及效率，本文选取 CFD -2 工况作为基本网格。

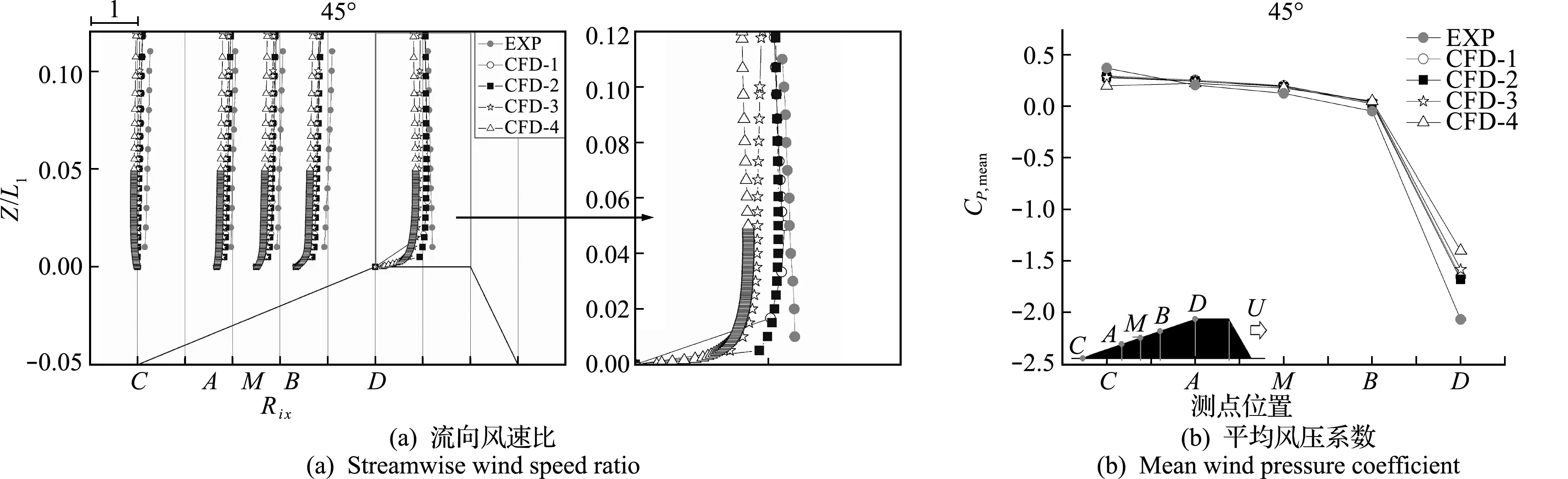
图4 网格分辨率的影响

常用的湍流模型有Standardk-ε,RNGk-ε和Realizablek-ε模型，其中后两种更适用于强旋流或带有弯曲面壁流动问题[15]，限于篇幅，本文未列出方程具体形式，详见文献[15]。

图5为上述3种湍流模型的数值模拟结果对比，网格布置均采用了表1的 CFD -2 工况，可以看出，(1) 对于流向风速比来说，除坡顶D点外，3种湍流模型的模拟结果无明显差别且与风洞试验具有较好的一致性；在坡顶D点，Standardk-ε湍流模型在数值上更接近于风洞试验，其次是Realizablek-ε湍流模型，而RNGk-ε湍流模型的计算结果与风洞试验差距最大。(2) 对于平均风压系数，不同湍流模型的数值模拟结果与风洞试验趋势基本一致；在坡顶分离点D处，3种湍流模型的模拟结果均与风洞试验结果有一定差距，Realizablek-ε湍流模型较其他两种湍流模型与风洞试验更接近。

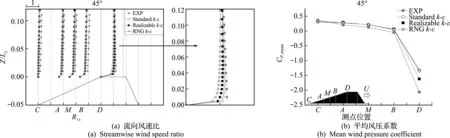
图5 湍流模型的影响

综上可见，Realizablek-ε湍流模型结果更接近风洞试验，后续的数值模拟采用该湍流模型。

4 坡顶局部光滑方法的影响

上述CFD数值模拟与风洞试验结果的差距在坡顶处最明显，这是因为坡顶处采用了折线模型，相对加剧了流动分离所致。下文详细讨论分离点D处不同局部光滑曲线方法的影响。

4.1 局部光滑曲线介绍

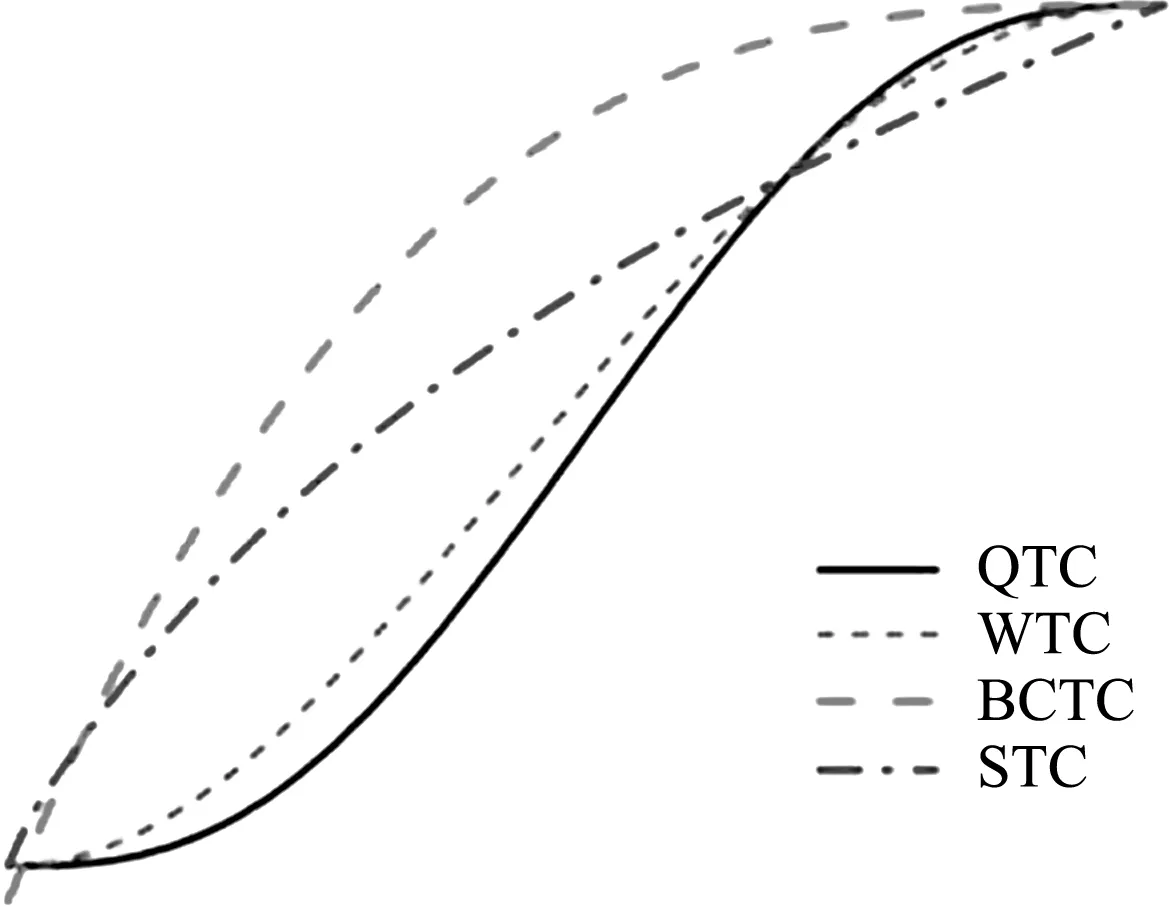
根据研究对象的特点，对坡顶的局部光滑选取了4种较常用的光滑曲线，其中前3种，双三次转变曲线BCTC(Bi-cubic transition curve)、定量过渡曲线QTC(Quantic transition curve)和维茨辛斯基曲线WTC(Witoszynski transition curve)已应用于大尺度边界的过渡光滑[16]，其相关表达式详见文献[16]，本文进一步讨论此3种曲线对局部地形光滑的适用性。为确定最优局部光滑曲线形式，还选取了具有二阶连续的光滑过渡曲线STC(Second-order transition curve)，其求解公式为

f(x)=xn(1-n)(a+bx)+cx

(2)

式中0

(3)

式中(x0，z0)为分离点D的坐标。经试算，当n=0.5，θ=30°时，STC光滑曲线模拟结果最佳。

4.2 不同局部光滑曲线CFD模拟结果

采用上述4种光滑曲线，在分离点D处选取过渡段水平长度L=25 mm分别进行局部光滑，如图6所示，图7为相应的数值模拟与风洞试验结果对比。

图6 局部光滑曲线

图7 局部光滑曲线的影响

可以看出，(1) 对于流向风速比，未经局部光滑的模拟结果在Z/L1=0.045以上才能与风洞试验结果的趋势一致，而基于4种光滑曲线模型的模拟结果均在更靠近地面的Z/L1=0.025处开始与风洞试验趋势保持一致，说明了坡顶分离点位置采取局部光滑的有效性和必要性。在分离点D处的近壁区(局部放大图)，WTC模型结果最大，STC和QTC模型在数值上更接近于风洞试验，误差也在可接受范围。(2) 对于平均风压系数，数值模拟结果与风洞试验趋势均基本一致，差别体现在分离点D处，其中基于WTC曲线的局部光滑模型的平均风压系数绝对值最大，BCTC曲线次之，而基于STC曲线的局部光滑模型与风洞试验的吻合性最好。

由此可见，基于STC曲线(参数值n=0.5，θ=30°)的局部光滑模型与风洞试验结果一致性相对更好。下面从几种光滑曲线的数学特征上分析STC曲线模拟结果精度相对较高的原因。

对于本文研究的高度简化典型二维山坡地形，其迎风面(坡面)为陡峭斜坡，若与山顶(水平面)的连接为折线，则连接点左右斜率不相等，即数学上的一阶不连续。气流流动受斜坡挤压，流速增大而压强相应减小，产生顺压梯度；坡顶分离点处气流速度最大而压强最小，存在逆压梯度，较大的逆压梯度会产生流动分离，即分离点处几何上的一阶不连续，导致分离点附近出现流动分离和转捩现象[17]。为保证气流经过山坡分离点时，不受速度不连续和压力突变的影响，需要满足速度连续性，即一阶连续；此外，流体黏性的特点还需要满足分离点处加速度的连续性，即二阶连续。上述4种曲线，仅STC曲线同时满足一阶和二阶连续，所以过渡光滑效果更好。

图8为不同模型的速度矢量图和平均风压系数云图，可以看出,(1) Unsmooth模型在分离点D处风压绝对值明显小于其他几种模型，且最大负压范围在分离点D处后方区域，说明在分离点处Unsmooth模型产生了逆压梯度；其他几种模型的最大负压范围均在分离点D处，说明分离点处采取具有一阶连续特性的曲线进行局部光滑能够消除逆压梯度，从而一定程度减弱该处的流动分离现象。从分离点D处的最大负压范围来看，4种局部光滑模型中STC模型最小，说明其在分离点处对流动的影响最小。(2) 对于近壁区的流向风速，在分离点D处及坡顶下游区域，Unsmooth模型的速度发生了明显的突变，BCTC，QTC和WTC模型也非均匀减小，这是分离点范围内的流动分离导致的流速突增所致；相比之下，STC模型由于具有二阶连续的特点，气流在经过分离点D处时其流速呈现均匀变化，在坡顶后方流动也更早趋于稳定，从而确保了STC模型与试验结果具有更好的一致性。

图8 速度矢量和平均风压系数云图

4.3 光滑曲线水平过渡段的影响

本文采取的坡顶光滑是在分离点处局部位置，下面分析STC曲线过渡光滑段范围的影响。由式(3)可知，STC光滑曲线只与x的取值范围有关，因此仅考虑水平长度的影响。由于结果差异主要在分离点，因此这里仅分析位置D处的风速比和平均风压系数绝对值，如图9所示，图中STC-25,STC-15和STC-10分别表示过渡光滑段水平长度取x=25 mm,15 mm和10 mm。

图9 不同过渡段水平长度对分离点处水平风速比和平均风压系数的影响

可以看出，对于水平风速比，整体上光滑过渡段不同水平长度的数值模拟结果与试验结果的一致性均优于未局部光滑模型(Unsmooth)，其中STC-10工况的模拟结果与风洞试验更吻合；从平均风压系数绝对值的比较来看，基于STC-10模型的数值模拟结果与风洞试验更为接近。可见，STC曲线过渡段水平长度对模拟精度有一定的影响，且光滑过渡段水平长度越短，模拟精度相对越高。

5 地形加速效应的规范及实验对比

地形加速效应是各国规范中典型二维山坡模型的主要参数，本节将数值模拟所得坡顶位置D处的地形加速效应，分别与文献[4]实验以及美国、中国、日本和欧洲等多个国家规范中规定的地形加速效应进行了对比。地形加速效应计算公式为

Ri x=U(x,z)/U0(z)

(4)

式中U(x,z)为坡顶位置的平均风速，U0(z)为对应高度处来流平均风速。图10为数值模拟所得坡顶地形加速效应与各国规范的对比。

图10 CFD地形加速效应与各国规范对比

可以看出，地形加速效应的各国规范值、数值模拟和试验结果之间均有所不同，随距地高度的增加逐渐趋于一致且数值接近1.0，但在近壁区差距较大。本文模拟所得近壁区的地形加速效应值与文献[4]实验值以及中国和澳大利亚规范值更为接近，尤其是STC曲线光滑模型结果(STC-10)在距地Z/H≥0.3时即能取得较好的一致性，而未局部光滑模型结果(Unsmooth)则在Z/H≥0.6位置才能与规范值逐渐趋于一致。由此也说明，STC曲线相对更适用于二维陡峭山坡的局部光滑。

6 结 论

(1) 在网格分辨率和湍流模型的影响方面，采用 CFD -2 网格分辨率以及Realizablek-ε湍流模型与风洞试验有较好的一致性，随着网格的进一步加密，数值模拟结果的精度没有显著提高。

(2) 在坡顶分离点处进行局部光滑处理，可较明显地提高该位置处的数值模拟精度，但建议选取具有二阶连续的STC曲线，且光滑过渡段水平长度越短，模拟精度相对越高。

(3) CFD数值模拟所得坡顶地形加速效应与文献试验以及各国规范在坡顶分离点的近壁区有一定差距，随着距地高度增加，基于STC局部光滑的模拟结果与规范值趋于一致，且与文献实验结果以及中国和澳大利亚规范结果的一致性更好。