基于神经网络算法的建筑结构振动分散控制研究

汪 权， 王 文， 韩新节， 韩强强， 周超杰

(1.合肥工业大学 土木与水利工程学院，合肥 230009；2.土木工程防灾减灾安徽省工程技术研究中心,合肥 230009)

1 引 言

目前结构振动控制形式中，分散控制是针对集中控制中一旦中央处理器损坏会导致整个控制系统失效的缺陷所提出的，若想取得更精确的控制效果，应考虑分散控制各子系统间的信息共享问题，即控制耦合问题。神经网络算法则是依托大量的数据进行反复训练来构建一个近似于原模型的网络结构，不需要传统控制算法依赖的精确数学模型，但缩减训练成本是其能否拓展工程应用领域的关键。

建筑结构振动分散控制考虑各子结构相应子系统耦合问题的研究取得了一定的成果。文献[1-4]基于传统控制算法实现了建筑结构振动分散控制形式下的各子系统控制耦合问题，汪权等[5，6]将包含原理与线性二次型最优控制原理和H∞鲁棒控制相结合，通过扩展分解控制系统及协调收缩获得重叠分散控制器，虽然控制效果良好，但算法需要建立控制结构对象的精确数学模型进行推导，较为复杂。

神经网络极强的非线性映射特性、信息并行处理、自学习和泛化能力使其在建筑结构振动控制领域得到了广泛应用。文献[7-11]用神经网络算法预测了地震作用下结构的未来响应，取得了较好的控制效果，但忽视了其在集中控制下的训练成本等问题。

目前人工神经网络模型有数十种之多，其中较为典型的有BP和RBF神经网络等，汪权等[12]将BP神经网络和分散控制相结合，成功应用于20层Benchmark结构模型，该方法能简化神经网络的结构且能有效地控制结构振动响应，并消除时滞，但未指出神经网络与分散控制相结合是否考虑了分散控制中的控制耦合问题。杜永峰等[13]在结构动力响应预测方面指出RBF神经网络学习速度更快，动态仿真性更强。潘兆东等[14]借助RBF神经网络通过设置全局控制器消除了子系统间的关联耦合。

本文将RBF神经网络与分散振动控制相结合进行研究，主要包括设计考虑各子系统间耦合作用的RBF神经网络算法近似模型，同时通过数值计算分析其神经网络算法的训练量。选取20层Benchmark建筑结构模型为对象，分别进行了集中控制和将结构分别划分为2个、4个及5个子结构的分散控制[5]，比较分析基于RBF神经网络算法的分散控制效果及训练次数。

2 RBF神经网络结构模型

本文RBF神经网络采用单隐层的三层前馈型神经网络，其网络结构包括输入层、隐含层和输出层。其隐含层的激活函数采用径向基函数，输出层的激活函数采用线性函数，其网络结构如图1所示。

图1 RBF神经网络结构模型

网络的输入层包括n个神经元节点连接信号的输入，输入向量为X=[x1,x2,…,xn]T；隐含层包括q个神经元节点，将输入信号转换到隐含层空间，隐含层输出向量为V=[v1,v2,…,vq]T，G(·)表示径向基函数；输出层包括m个神经元节点，输出层的输出向量为Y=[y1,y2,…,ym]T，输出层的激活函数常采用线性激活函数。

期望输出向量为D=[d1,d2,…,dm]T。隐含层到输出层的权值矩阵为Wj k，表示隐含层第j神经元到输出层第k神经元的权值。

网络隐含层采用径向基函数，采用高斯函数,

G(x)=e-‖x -c‖2/σ2

(1)

c与σ分别表示隐含层神经元径向基函数的数据中心点宽度参数，‖·‖表示距离函数。

从隐含层到输出层为线性输出，输出为

(k=1,2,…,m)(2)

式中bk为输出层神经元的阈值向量。

3 RBF神经网络学习算法

采用MATLAB软件的newrb函数来构建RBF神经网络，其表达式为

经研究表明，观察组中老年糖尿病合并脑梗塞患者检出率90.00%（阴性患者10例、百分比为10.00%；阳性患者90例、百分比为90.00%）高于对照组检出率80.00%，差异有统计学意义（P＜0.05）。

net=newrb(P,T,goal,spread,MN,DF)

(3)

newrb的算法是在有输入向量P与输出向量T的情况下，先预设好期望误差、扩展速度S以及每次隐含层神经元节点个数增加次数，然后假定初始隐含层无神经元节点，把开始误差最大的输入向量作为权值向量(即数据中心c)，可计算出隐含层输出向量V，并根据隐含层输出向量V与T以最小误差为目的对输出层权重Wj k与bk进行修改(采用最小二乘法)，最后依次增加隐含层神经节点个数重复进行上述运算，直到网络的误差降到预期误差以下或达到最大训练次数。

扩展速度S越大，函数的拟合就越平滑，且过大或过小的S均需要非常多的神经元以适应函数的快速变化或缓慢变化。本文通过试算来确定扩展速度S，首先将集中控制及分散控制的第一个子系统期望误差设为1×10-7，而分散控制的其他子系统由于数据较集中且控制数据少，在保证总体误差的情况下可适当减小平均误差(期望误差)；然后在newrb函数中不断调整扩展速度S来比较训练后的训练次数与训练误差，从而得出一个较优值。

4 算 例

为了验证建筑结构分散控制与RBF神经网络相结合所设计的考虑各子系统耦合作用的RBF神经网络模型的控制效果，以及分析该网络模型的计算成本，将该算法应用于20层Benchmark抗震钢结构模型控制对象，使用的神经网络辨识器和控制器均是RBF神经网络，该模型结构具体的楼层质量、刚度参数和结构布置等详见文献[15]。

4.1 RBF神经网络结构

神经网络辨识器输入为前两个时刻结构1～20层每层的位移、速度、当前时刻每层的控制力和地震加速度，故其神经元节点数为2*(20+20)+20+1=101；输出为下一时刻结构1～20层每层的位移、速度和加速度响应，故其神经元节点数为 20+20+20=60。RBF神经网络辨识器取期望误差MSE=1.0×10-8，径向基函数的扩展速度试算为S=100，隐含层神经元个数由网络训练自动确定为16，达到的训练误差为 MSE=4.2487×10-9。综上RBF神经网络辨识器的网络结构为101*16*60。

神经网络控制器输入为辨识器得出的下一时刻结构1～20层每层的位移、速度响应和地震加速度，输出为下一时刻结构1～20层每层的控制力。

对于神经网络集中控制器设计，取期望误差MSE=1.0×10-7，径向基函数的扩展速度试算为S=5.2，隐含层神经元个数可由newrb函数在建立并训练RBF神经网络控制器的过程中自动确定为25，训练误差为MSE=7.69795×10-8，综上RBF神经网络集中控制器的网络结构为41*25*20。

对于神经网络分散控制器设计，分别将结构每10层(Case 1)、 每5层(Case 2)和每4层(Case 3)划分为1个子系统，如图2所示三种工况进行研究。

图2 子系统划分工况

Case 1: 将结构从1～10层和11～20层划分为两个子系统。

Case 2: 将结构从1～5层、6～10层、11～15层和16～20层划分为四个子系统。

Case 3: 将结构从1～4层、5～8层、9～12层、13～16层和17～20层划分为五个子系统。

以上分散控制的三个工况各子系统神经网络控制器径向基函数的期望误差及扩展速度列入表1，隐含层神经元个数同理可由newrb函数在建立并训练RBF神经网络控制器的过程中自动确定，训练误差和神经网络分散控制器的网络结构列入表1。

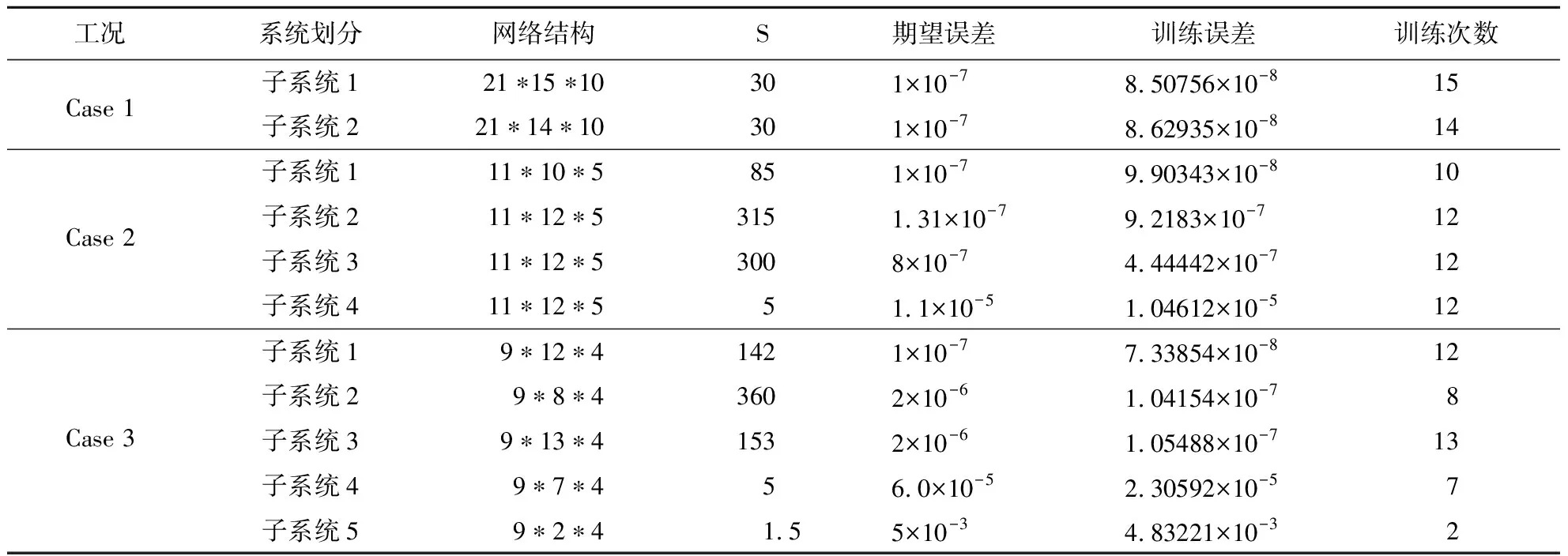
表1 分散控制各子系统RBF神经网络结构模型信息Tab.1 RBF NNC model information of each subsystem under decentralized control

4.2 RBF神经网络分散控制效果

RBF神经网络辨识器和控制器的训练数据分别采用20层Benchmark模型结构在地震激励El Centro(NS，1940)波(加速度峰值为3.147 m/s2)作用下，由 LQR算法计算得到的结构地震响应前500个采样时刻数据(采样周期为0.02 s)。本文采用MATLAB的Simulink模块进行数值仿真，以Case 3为例，该分散控制系统如图3所示。

图3 神经网络分散控制系统(Case 3)

为了评价RBF神经网络分散控制效果，同时验证神经网络控制器的自学习和泛化能力，在采样步长0.02 s，持时30 s的地震激励Kobe(NS，1995)波(加速度峰值为8.1782 m/s2)作用下，计算RBF神经网络分散控制各工况下的结构地震响应，并与神经网络集中控制结果进行比较。

图4和图5分别给出了各工况下结构在两种地震波作用下的结构响应和控制力。表2给出了地震作用下各工况结构的位移和加速度峰值。由表2可知，本文研究的RBF神经网络分散控制对结构的位移和加速度响应具有良好的控制效果。在各种控制工况下，其结构控制响应与集中控制相差不大，表明分散控制可达到与集中控制近似的效果。

图4 El Centro作用下受控结构的地震响应与控制力

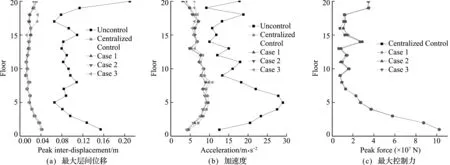
图5 Kobe作用下受控结构的地震响应与控制力

5 RBF与BP神经网络分散控制对比

RBF神经网络分散控制策略考虑了子系统耦合作用且取得了较好的控制效果，为进一步说明本文方法在控制效果和计算成本方面的优势，选取部分计算结果与文献[12]进行对比分析。

5.1 控制效果

限于篇幅，仅比较Kobe波作用下结构采用RBF和BP神经网络分散控制的位移与加速度反应峰值。由表2可知，结构在Kobe波作用下，通过分散RBF神经网络振动控制的各工况位移和加速度峰值响应均比分散BP神经网络小，说明前者在控制效果上比后者有一定优势。

表2 El Centro和Kobe作用下各工况结构的位移和加速度反应峰值及RBF和BP在Kode作用下的控制效果对比Tab.2 Peak displacement & acceleration under El Centro and Kobe and comparison of the control effect of RBF and BP under the Kode

5.2 计算成本

神经网络计算成本可由控制系统训练次数进行判断，由表1可知，RBF神经网络下结构分散控制的三种划分情形中case 2各子系统训练量比case 1少，虽然case 3个别子系统训练次数比case 2多，但相差不大。

为进一步说明RBF神经网络分散控制在计算成本问题上的优势，本文将各子系统平均训练次数与BP神经网络分散控制[12]进行对比，列入表3。

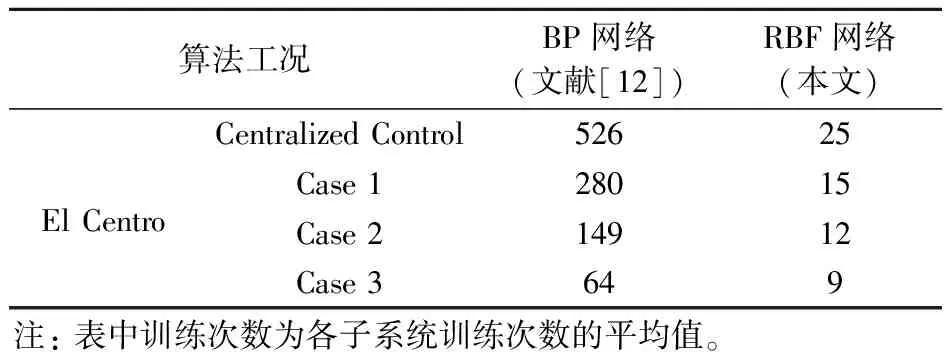
表3 El Centro作用下结构各工况神经网络平均训练次数

由表3可知，本文采用的RBF神经网络在训练次数上显著低于BP网络，计算成本大幅度降低；同时，表3各子系统平均训练次数随子系统划分数量的增多而减少，RBF网络与分散控制相结合具有更大优势。

6 结 论

本文研究了RBF神经网络在建筑结构振动分散控制中的应用，考虑子系统控制耦合问题以及神经网络训练成本问题，在神经网络辨识器和控制器均采用RBF神经网络的情况下，将选取的20层Benchmark模型分别划分为2个、4个和5个子系统进行研究，并将数值仿真结果与同样采用RBF神经网络的集中控制进行对比分析。结果表明，RBF神经网络算法用于结构振动分散控制具有良好的控制效果，而且RBF网络较BP网络学习能力更强，与分散控制结合时控制效果更优且计算成本大幅降低，说明RBF神经网络分散控制更适用于实际工程。同时，本文将神经网络与分散控制相结合，局部控制器损坏不会导致整个控制系统失效，提高了控制系统在实际工程中应用的可靠性。