基于改进樽海鞘群算法的磁流变减摆控制优化

王 博，王璐琦，祝世兴

(1.中国民航大学 工程技术训练中心，天津 300300； 2.中国民航大学 航空工程学院，天津 300300)

引言

摆振是存在于飞机起落架的有害振动现象[1]。磁流变(Magnetorheological,MR)阻尼器通过改变外加电场调整输出阻尼，具有能耗低、响应快、阻尼连续可控等优点，在起落架减摆领域具有较大应用前景[2-3]。决定MR阻尼器减摆性能的关键是根据机轮摆振状态设置合适的控制电流。PID控制器由于结构简单、可靠性高，被广泛应用于磁流变阻尼器的控制，科学合理的设定控制器参数对于MR阻尼器的减摆效果尤为重要[4-5]。

控制参数工程整定方法繁琐且准确性低，近年来随着智能算法的兴起，众多学者利用智能算法优化调整磁流变阻尼器的控制参数[6]。GAD S等[7]利用遗传算法(Genetic Algorithm，GA)整定汽车座椅磁流变减振系统的PID参数，系统设计过程中利用GA实现控制参数寻优，简化整定过程，减小人为因素对参数准确性影响，提高了控制精度。METERED H等[8]为提高汽车磁流变半主动悬架的舒适性和稳定性，通过粒子群算法(Particle Swarm Optimization，PSO)搜索控制器的最优参数，并验证了方法的可行性。TALIB M H等[9]提出一种高级萤火虫算法(Advanced Firefly Algorithm，AFA)，用以优化磁流变悬架系统的控制参数，改善了系统的减振性能。但GA，PSO，AFA等经典算法存在复杂度高、收敛速度慢、全局搜索能力差、参数多且调整过程主观性强等问题，会增加整定过程耗时，降低参数精度和优化效率，并最终影响系统控制效果。

樽海鞘群算法(Salp Swarm Algorithm，SSA)是MIRJALILI S等[10]提出的一种新型智能优化算法，采用链式寻优结构，群体链前部和后部的个体采取不同进化方式。SSA由于复杂度低，灵活性强，且基本无需参数设置，最大程度减少了主观因素干扰，在控制参数优化领域具有较好的应用前景[11-12]。丁力等[13]、HASANEN H 等[14]分别应用SSA优化四旋翼飞行器的姿态控制参数及电力系统负荷频率控制参数，实验表明，优化后的控制器具有更好的控制精度。但在SSA种群更新过程中，由于群体链前部的领导者主要依靠精英个体引导，种群进化多样性不足，容易陷入局部最优；而群体链后部的跟随者缺少优质个体指引，进化过于盲目，易导致算法优化效率降低，直接影响SSA的参数优化效果。

因此，本研究对SSA采取两项改进措施：通过精英个体杂交变异策略实现领导者位置更新，增强全局搜索能力；跟随个体更新过程中加入自适应差分变异操作，提高优化效率。进而，提出改进樽海鞘群算法(Modified Salp Swarm Algorithm，MSSA)，并以起落架摆振绝对误差时间乘积积分和摆振第3周期最大位移与时间积作为适应度函数，将MSSA应用于磁流变减摆系统控制参数优化问题。通过与SSA，AFA，PSO，GA 4种算法对比实验，表明MSSA算法的优化效率及精度更高，鲁棒性更强，经MSSA优化后的MR减摆系统摆振控制效果更好。

1 樽海鞘群算法

SSA通过模拟樽海鞘在海洋中群体链式运动行为搜索问题的最优解[15]，算法将种群个体分为领导者和跟随者，两类个体采取不同运动更新方式：领导者位于群体链前部，根据精英个体位置引导种群移动；跟随者位于群体链后部，相互跟随运动[16]。SSA实现过程如下：

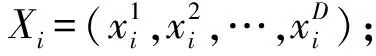
(2) 计算所有个体适应度值，根据适应度进行个体排序，选取当前最优个体作为精英个体G(t)；

(3) 选择种群前N/2个体作为领导者，即i≤N/2时根据式(1)更新领导个体位置：

(1)

c1=2e-(4t/tmax)2

(2)

(4) 选择种群后N/2个体作为跟随者，即i>N/2时根据式(3)更新跟随个体位置：

(3)

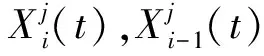
(5) 更新迭代次数t，判断是否达到最大迭代次数，若未达到跳转至步骤(2)，否则输出精英个体位置G(t)，即为全局最优解。

2 樽海鞘群算法改进

针对SSA的局部最优和优化效率低问题，本研究在SSA的领导者和跟随者更新过程中分别采取精英个体杂交变异、自适应差分变异两项策略改进算法性能，以增强全局搜索能力，改善优化效率。

2.1 精英个体杂交变异策略

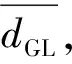
(4)

K=e-(fLr-fT/fG-fT)

(5)

式中，fLr为XLr(t)的适应度；fG，fT分别为当前种群个体适应度的最优及最差值；fLr与fG数值越接近表明XLr(t)的质量越高，此时K数值较大，进化信息中XLr(t)所占比例较高，有利于增加优质进化信息引导个体向更优位置移动。

为直观说明精英个体杂交变异策略对局部最优问题的改善效果，本研究以文献[19]中多峰函数Alpine为例，分别应用SSA和基于精英个体杂交变异策略的SSA对其连续优化50次，绘制平均收敛曲线，同时选取收敛精度最高的优化过程记录精英个体运动轨迹。测试过程中，算法参数设置一致，tmax=100，N=100，D=3。图1所示为两种算法平均收敛曲线，为便于观察，纵坐标对适应度均值favr取10为底的对数。可以看出，SSA的优化初期、末期由于陷入局部极值，优化趋于停滞状态，经过约20次迭代才跳出局部最优；而基于EHM的SSA优化过程中能够快速跳出局部极值区域并保持较高的收敛速度，收敛精度明显优于SSA。通过图2所示精英个体运动轨迹对比，进一步可知2种算法初始精英个体位置基本一致的情况下，基于EHM的SSA种群个体搜索范围更广，基本不会陷入局部极值区域，能够快速收敛到理想目标个体邻域且与理想值更接近。上述实验对比表明，精英个体杂交变异能够避免单一精英个体对种群进化的误导，提高进化多样性，增强全局搜索能力。

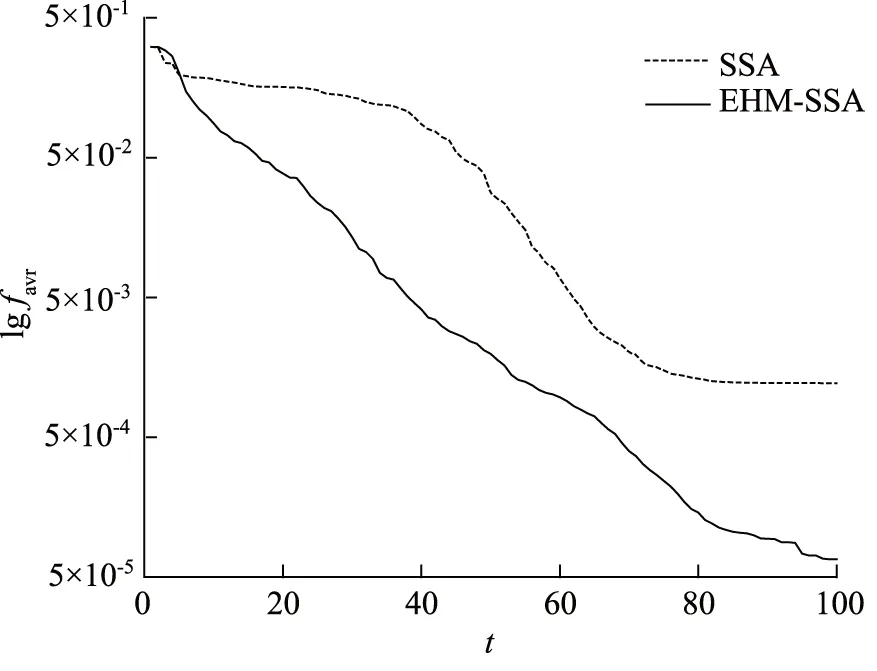
图1 Alpine函数平均收敛曲线Fig.1 Average convergence curve of Alpine function

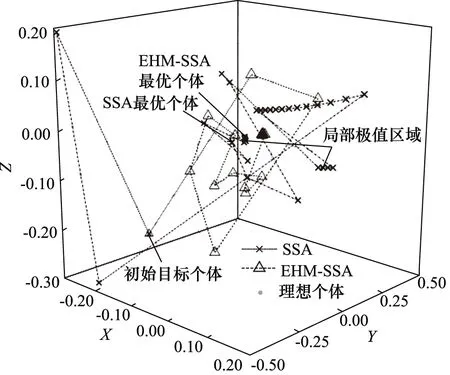
图2 精英个体进化轨迹Fig.2 Evolutionary trajectories of elite individuals

2.2 自适应差分变异策略

SSA算法只是机械的将位于樽海鞘链后部的个体作为跟随个体，其更新只依赖于当前位置以及与之相邻的樽海鞘位置。采用此更新方式，适应度较好的跟随者由于缺少目标位置信息，无法及时收敛到全局最优解，而适应度差的跟随者缺少与其他个体的信息交换，不能充分地进行全局搜索，最终易导致算法收敛速度减小，优化效率下降。针对此问题，本研究提出跟随者的自适应差分变异策略，将适应度优于当前均值的跟随者作为优质个体，其余跟随者为非优质个体，对于优质个体利用最优个体与跟随者进行差分变异完成更新操作；非优质个体则随机选取种群个体与跟随者进行差分变异实现个体更新。改进后的跟随者(i>N/2)更新公式如下：

(6)

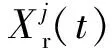
3 MSSA的MR减摆控制参数优化

3.1 起落架MR减摆控制数学模型

摆振是飞机滑跑过程中，受起落架扭转力、轮胎弹性变形和轮胎-跑道道面耦合作用影响，前起落架机轮偏离中心位置的周期性往复运动[20]。图3所示为安装磁流变减摆器的某型无人机前起落架结构模型。

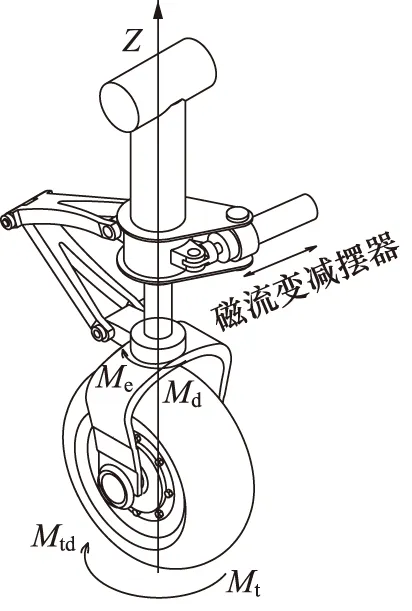
图3 飞机前起落架结构模型Fig.3 Structural model of aircraft nose landing gear

通过受力分析，可建立轮胎动力学方程和起落架扭转力学方程，分别如式(7)、式(8)所示，二者共同构成起落架磁流变减摆数学模型[21]：

(7)

(8)

式中，s为机轮触地点侧向位移；l为机轮触地长度；σ为轮胎侧向松弛长度；V为飞机滑跑速度；φ为机轮的摆动角度；θ为轮胎侧滑角；Iz为支柱的惯性矩；Me为扭转刚度引起的线性弹性力矩；Md为支柱扭转阻尼力矩；Mt，Mtd分别为轮胎的侧向变形力矩和阻尼力矩；Mmd为磁流变减摆阻尼力矩，如式(9)～式(13)所示:

Me(φ)=Cφ

(9)

(10)

Mt(θ)=Mz(θ)-eFs(θ)

(11)

(12)

Mmd=fmr*d

(13)

式中，C为起落架支柱扭转刚度；ks为支柱扭转阻尼系数；kt为机轮胎面阻尼系数；e为机轮的有效稳定距；d为减摆力臂长度；fmr为MR减摆器的输出阻尼力，主要与外加电流相关，采用文献[22]中基于正弦拟合建立的磁流变阻尼器力学模型表示；Fs(θ)代表机轮的侧偏力，Mz代表机轮回正力矩，分别表示如下：

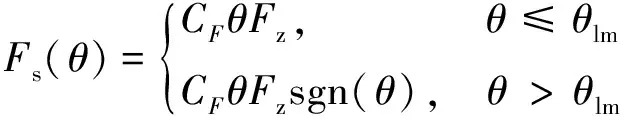
(14)

(15)

式中，CM，CF分别表示机轮的回正力矩系数和侧偏力系数；θam，θlm分别表示机轮的自回正临界侧滑角和侧偏力的临界角；Fz为垂直载荷。

由起落架磁流变减摆模型可知，MR减摆器可通过调节减摆器线圈回路电流改变减摆阻尼以控制摆振。为使MR减摆器有效减小摆振，本研究采用PID控制策略。将T时刻机轮触地点侧向位移s(T)作为系统反馈，以此时减摆器线圈回路电流I(T)为被控对象，根据系统控制模型调节线圈回路电流，进而调整MR减摆器的输出阻尼，使机轮的摆动幅度最小，实现减摆控制。系统控制模型可表示为：

(16)

式中，Kp—— 比例调节系数

Ki—— 积分调节系数

Kd—— 微分调节系数

合理设定这3个参数是系统获得良好控制性能的关键。

3.2 优化目标

为提高磁流变减摆控制参数的准确性，改善控制效果，简化控制参数的调整过程，本研究利用改进后的樽海鞘群算法优化控制器的3个参数Kp，Ki，Kd。将一组控制参数作为一个种群个体，利用适应度评估不同参数组合下控制器的减摆效果，通过算法的反复迭代搜索适应度值最优的参数，以期达到最优减摆控制。

根据《飞机前起落架防摆设计要求》，飞机前起落架摆振应在3个周期内进入临界稳定状态，摆幅至少衰减到最大初始振动幅度的1/4。磁流变减摆控制的最终目标是尽可能减小起落架摆振幅度，并在规定时间内将摆幅收敛到摆振临界稳定域，使起落架逐渐趋于稳定。因此本研究综合考虑起落架的稳态误差、摆振第3周期振幅衰减情况和系统调节时间，计算时间侧向位移乘积的积分(即ITAE指标)以及摆动发生第3周期最大位移与时间积，将二者之和作为适应度函数，其公式如下：

(17)

3.3 MSSA的控制参数优化步骤

MSSA的磁流变减摆控制参数优化流程如图4所示，具体步骤如下：

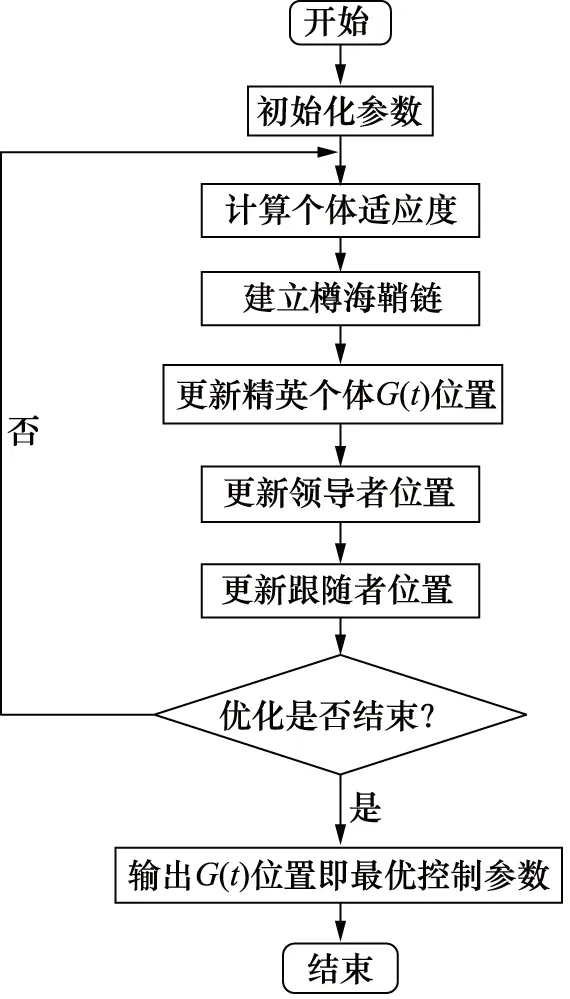
图4 基于MSSA的MR减摆控制参数优化流程图Fig.4 Flow chart for optimization of MR shimmy control parameters based on MSSA

(1) 初始化参数，樽海鞘个体的初始位置，最大迭代次数tmax，种群规模N，个体维度D=3；

(2) 计算个体适应度，分别将樽海鞘个体位置赋值控制器，运行磁流变减摆控制模型，依式(17)计算所有个体的适应度；

(3) 建立樽海鞘链，按照适应度值优劣，降序排序种群个体建立樽海鞘链，前半部分个体为领导者，后半部分为跟随者；

(4) 更新精英个体位置，选取当前适应度最优个体为精英个体G(t)；

(5) 更新领导者位置，随机选取领导个体XLr(t)，依式(4)杂交变异更新领导者位置；

(6) 更新跟随者位置，随机选取种群个体Xr(t)，根据式(6)更新跟随者；

(7) 判定优化结束条件，若迭代次数已达到tmax，输出精英个体位置即最优控制参数，否则返回步骤(2)。

4 仿真实验及分析

4.1 基本优化性能测试

本研究为测试MSSA的有效性及稳定性，选取6个标准函数，以MATLAB 2016b为仿真环境进行实验测试，并与SSA，AFA，PSO，GA对比实验，所选测试函数如式(18)～式(23)所示，理论最优值均为0，其中F1～F3为单峰值函数，F4～F5为多峰值函数。实验中5种算法的最大迭代次数tmax、种群规模N、个体维度D设置一致，分别为100, 100, 3；AFA算法的最大吸引度β0=1, 光吸收系数γ=2，步长因子α=0.2；PSO算法的个体学习因子c1=2，社会学习因子c2=2；GA算法的交叉概率pc=0.8，变异概率pm=0.15。5种算法针对每个函数分别独立运行500次，统计实验的均值、方差及最优值，如表1所示。

表1 测试函数优化结果Tab.1 Optimization results of test functions

(18)

(19)

(20)

-5.12≤xi≤5.12

(21)

(22)

-600≤xi≤600

(23)

通过分析表1数据可知，对于全部测试函数，MSSA的收敛精度和稳定性相较SSA有显著提升，且明显优于AFA,PSO，GA算法。特别是对于单峰值函数F1和多峰值函数F4，F6，MSSA的收敛精度比SSA分别提高了55，52，6×107倍以上，同时其在求解F4时取得了理论最优值，MSSA的收敛性能明显优于4种对比算法。

为更直观分析算法的优化过程，图5显示了实验中5种算法针对每个测试函数的平均收敛曲线。可以看出，MSSA的收敛速度明显快于4种对比算法，其可以利用每一次迭代寻找优质解，基本不会出现其他算法存在的收敛停滞情况，即使在迭代后期仍能够不断发现新的更优解。由此说明，MSSA通过自适应差分变异促进了种群个体根据自身特点进行充分的全局搜索和局部寻优，加快了收敛速度，使算法具有较高的优化效率，同时精英个体杂交变异策略也提高了全局搜索能力，避免了全局最优。综上表明，MSSA采取的两项改进措施有效，算法具有较高的收敛精度、优化效率和稳定性。

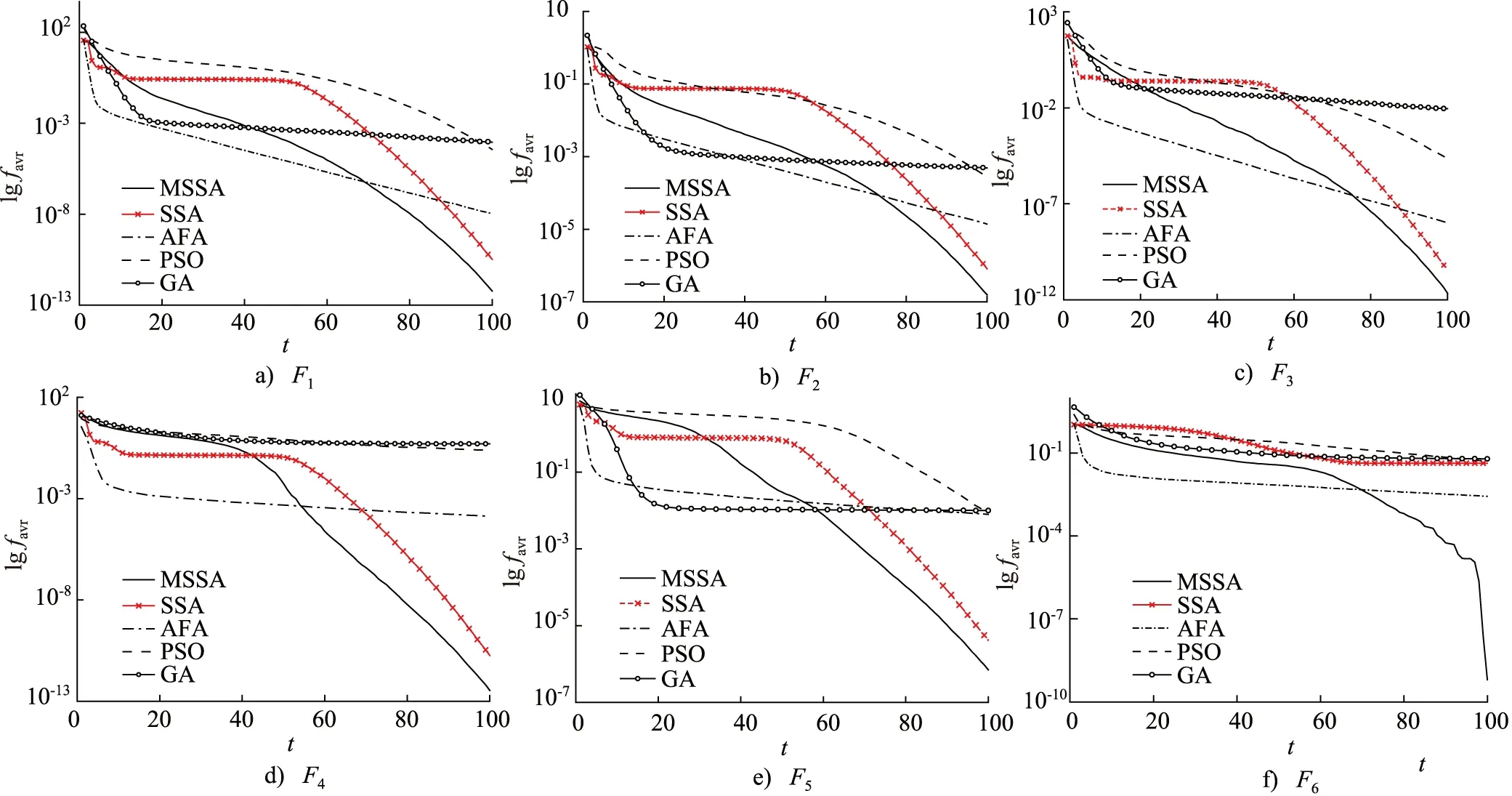
图5 测试函数平均收敛曲线Fig.5 Average convergence curve of test functions

4.2 MR减摆控制优化仿真实验

本研究为进一步验证MSSA对于起落架MR减摆控制参数的优化效果，利用MATLAB 2016b/Simulink搭建减摆控制模型，分别应用MSSA，SSA，AFA，PSO，GA优化仿真，并在飞机滑跑速度为30, 50, 70 m/s 状态下对比分析不同方法优化后的摆振控制性能。实验中模型参数如表2所示，种群规模、个体维度、最大迭代次数分别为30，3，100，控制参数Kp，Ki，Kd取值范围为[0, 100]，其他参数与4.1节中一致。实验计算机配置：CPU为Intel Xeon W-10885M(2.4 GHz)；内存为32 GB；操作系统为Win10(X64)。5种优化方法分别独立运行5次，对于每种算法分别选取1组适应度值最优的控制参数。

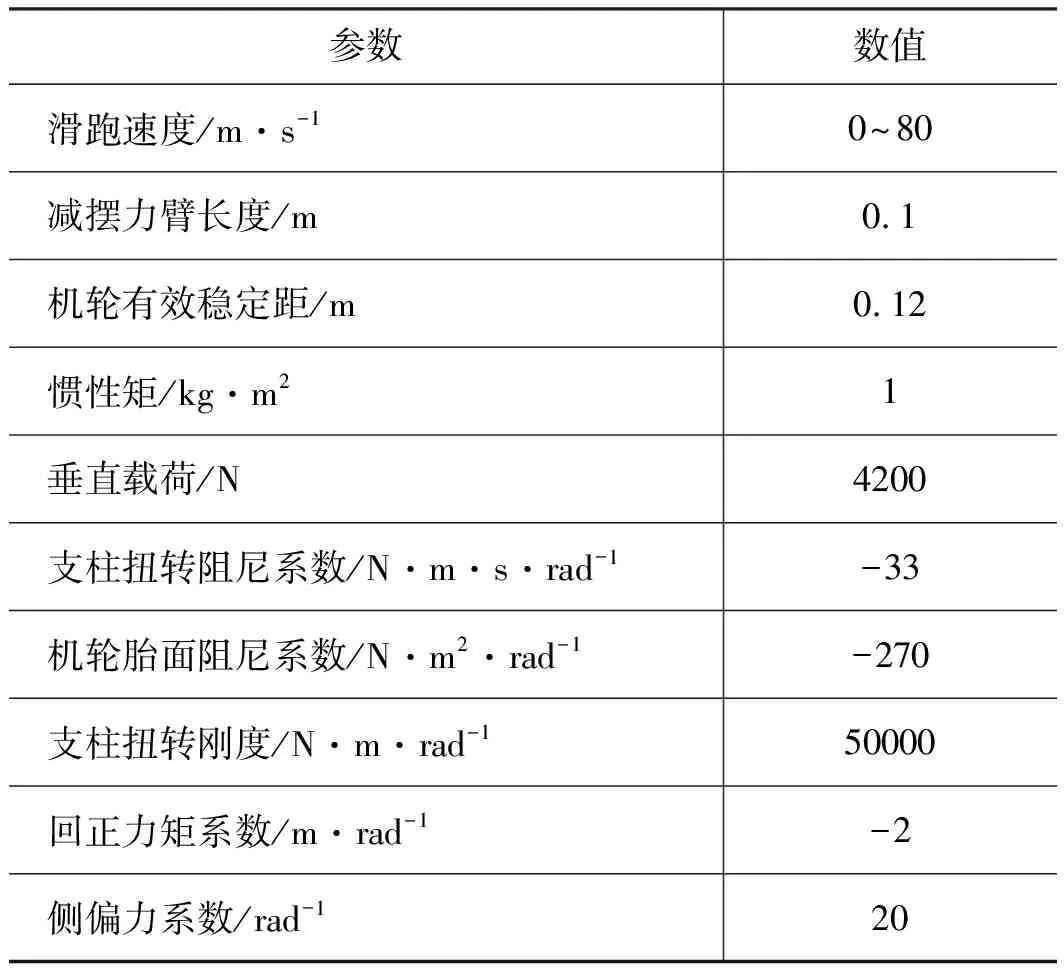
表2 模型参数Tab.2 Model parameters

表3为不同优化方法取得的最优适应度值及对应控制参数，5种方法迭代1次的平均运行时间如表4所示。可以看出，基于MSSA的优化方法获得的适应度值最佳，运行时间与SSA基本一致，且比AFA，PSO，GA缩短了5%以上，说明MSSA采取的改进措施提高了优化性能，基本没有增加SSA的时间复杂度，能够以较低的时间成本高质量完成优化任务。

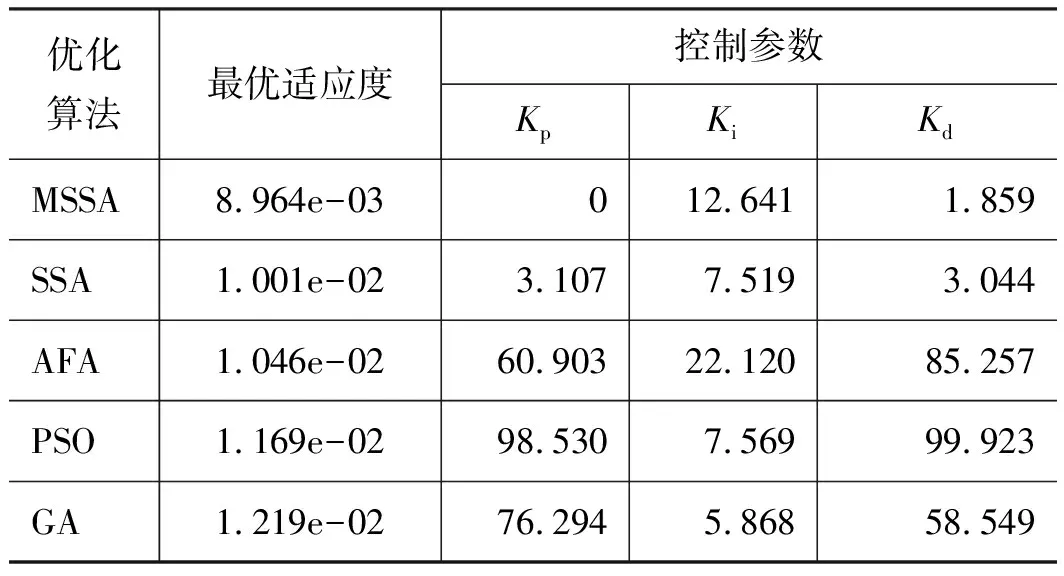
表3 最优适应度及优化后控制参数Tab.3 Optimal fitness and optimized control parameters

表4 算法平均运行时间Tab.4 Average running time of algorithms

机轮的平均侧向位移及摆振收敛时间如表5所示，侧向位移动态响应曲线如图6所示。通过表5可知，在飞机3种不同滑跑工况下，MSSA优化的MR减摆控制系统相较其余4种算法优化的控制系统，机轮平均侧向位移减小了4.24%～9.94%，摆振收敛时间缩短幅度可达33.19%，尤其是滑跑速度为50，70 m/s时，摆振收敛时间的改善幅度均达到30%以上。由图6可以看出，MSSA优化的MR减摆控制系统全部滑跑工况下，侧向位移都能够在摆振第3个周期收敛到最大初始值的1/4并快速衰减趋于稳定，且在整个摆振控制周期内侧向位移的幅度更小，而其他4种算法优化的减摆控制系统，滑跑速度为50，70 m/s时摆振无法在规定时间内收敛。由此表明，利用MSSA优化的MR减摆控制系统，减小了起落架摆振幅度，提高了摆振收敛速度，具有更好的摆振控制效果。

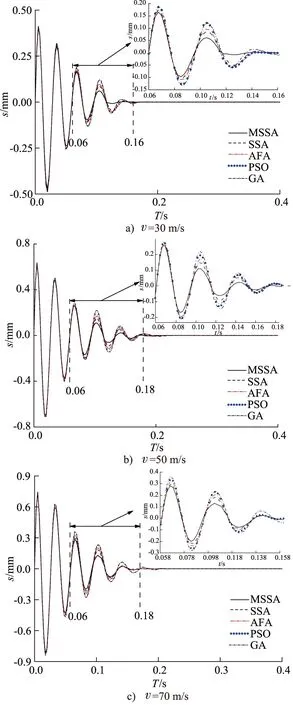
图6 机轮侧向位移动态响应曲线Fig.6 Dynamic response of lateral displacement

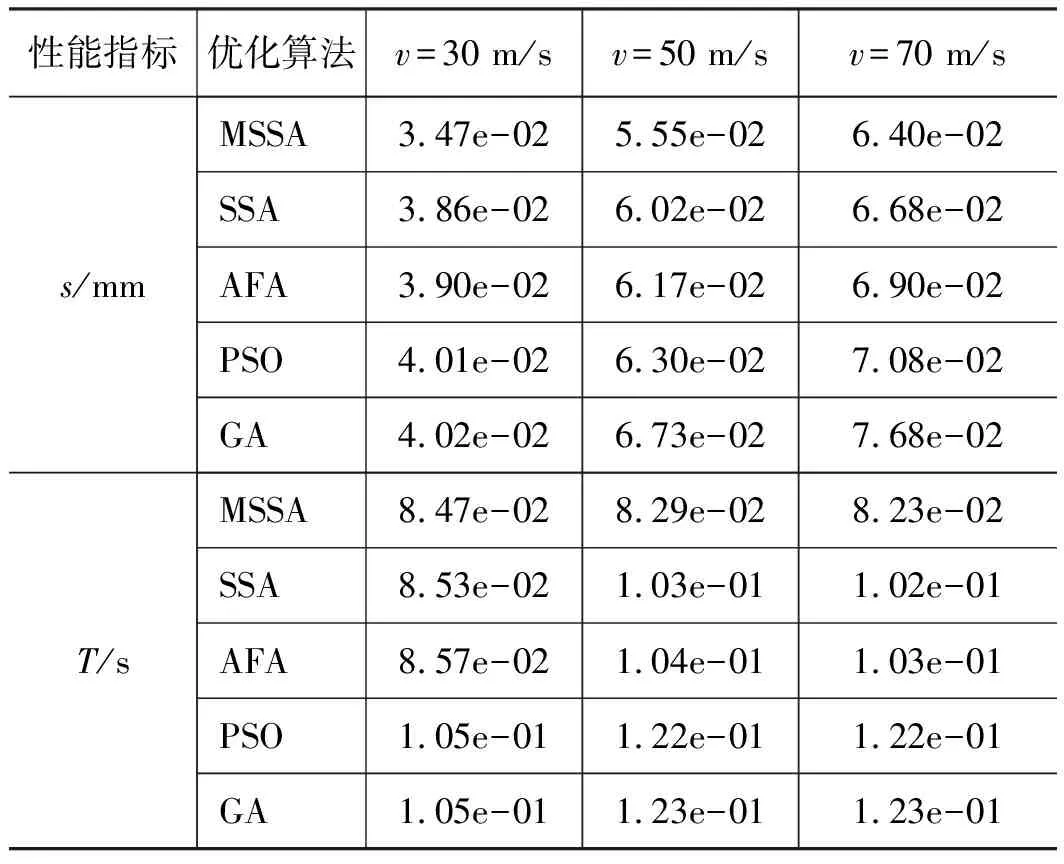
表5 减摆仿真实验数据Tab.5 Simulation data of shimmy control

5 结论

本研究为解决磁流变减摆控制参数整定方法存在的问题，提出一种基于改进樽海鞘群算法以优化MR减摆控制参数。针对SSA算法，在领导者位置更新过程中加入精英个体杂交变异策略，扩大种群进化范围，增强算法全局搜索能力；在跟随者更新过程中引入两种形式差分变异算子，根据个体适应度自适应选择差分操作，加快收敛速度，提高算法优化效率。在此基础上，按照摆振幅度最小、摆振稳定用时最短原则构建适应度函数，利用MSSA算法获取MR减摆系统的最优控制参数。最后，将MSSA与SSA, AFA,PSO,GA对比测试，选取6个标准函数测试算法基本性能，实验表明，MSSA的收敛精度和优化效率显著提升，优化性能在所有测试算法中表现最佳。进一步的控制优化仿真实验表明，基于MSSA的整定方法耗时较短，优化的MR减摆控制系统，相比其他4种方法摆幅更小，摆振收敛时间更短，减摆效果得到较大改善。