基于改进PSO算法的电液位置伺服系统MRAC跟踪控制

蔡改贫，曾常熙，周小云，刘 鑫

(江西理工大学 机电工程学院，江西 赣州 341000)

引言

作为一个典型的非线性系统，电液位置伺服系统有如下特征： ① 位置跟踪，表现为输出位移随输入的位移一同变化； ② 功率放大，表现为系统的输入功率小，而输出功率大并能带动较大的负载； ③ 是一个负反馈系统。由此，电液位置伺服系统得到了广泛应用，研究也显得尤为重要[1-3]。

近年来，为提高电液位置伺服系统的控制精度，国内外学者做了诸多研究。司昌练等[4]提出一种改进的模糊自适应控制算法，并通过仿真证明了该算法能提高电液位置伺服系统的响应速度和鲁棒性；何文清等[5]针对电液位置伺服系统，提出一种基于单神经元网络PID整定方法，发现单神经元PID整定控制精度高，整定时间短；刘希等[6]选取六自由度并联平台，设计自适应反演滑模控制器，再通过在阶跃信号和正弦信号下的仿真分析，证明了所设计控制器的有效性。

为进一步提升电液位置伺服系统的控制性能，DING Xingya 等[7]针对具有反馈信号传输延迟的电液位置伺服系统，提出一种混合控制器，并利用单自由度电液振动台论证了该控制器比比例积分导数和反推控制器有更好的控制效果。李文顶等[8]针对电液位置伺服系统中阀控液压缸位置伺服参数不确定的问题，设计出一种基于RBF神经网络的滑模控制器，并通过仿真证明了其具有较强的鲁棒性。母东杰等[9]将模型参考自适应控制器与阀控非对称缸电液位置伺服系统相结合，并通过仿真证明了所提方法能提高系统的响应精度。刘昌龙等[10]针对气动伺服系统，设计带有PD增益的模型参考模糊自适应控制器，并用仿真结果证明了该方法的有效性。

以上研究主要集中在电液位置伺服系统伺服控制器的设计上，未进一步考虑伺服控制器的参数优化问题。而在电液位置伺服系统中，控制性能的优劣与参数的选择息息相关。因此，为进一步优化其参数，在分析传统PSO算法、APSO算法不足的基础上，本研究提出一种改进的PSO算法，并将改进的PSO算法应用到模型参考自适应控制器中，进一步提升电液位置伺服系统的控制性能。最后，通过仿真分析论证了所提方法的可行性。

1 电液位置伺服系统数学模型的建立

电液位置伺服系统结构如图1所示。计算机给定一个输入R，将R与伺服液压缸位移Y对比，产生误差信号并将其反馈给控制器；误差信号经伺服放大器和电液伺服阀处理后控制伺服液压缸的位移Y。电液位置伺服系统的闭环控制可以通过这种循环来实现[11]。

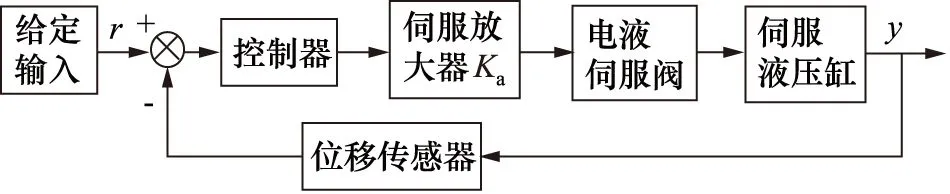
图1 电液位置伺服系统结构图

电液位置伺服系统的微分方程组为：

(1)

(2)

xv=KvKSu

(3)

式中，KQ,KS,Kv—— 流量、伺服阀和控制器的增益

KC,Ct,cp—— 控制窗口流量-压力系数、总泄漏系数和黏性阻尼系数

xv,xp—— 阀芯位移和活塞位移

p1—— 负载压差

Ap,Vt—— 活塞面积和总压缩容积

mt—— 活塞上总质量

βe—— 弹性模量

u—— 控制电压信号

FL—— 负载力

k—— 弹簧刚度

(4)

式中，r—— 输入信号

y—— 输出信号

由式(1)～式(4)，可推导出误差状态空间方程，即：

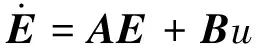
(5)

B—— 控制矩阵

2 模型参考自适应控制

2.1 模型参考自适应控制器的设计

给定控制器和参考模型(理想性能指标)一个信号r，系统通过对比参考模型和被控对象的输出来获得误差信息。当所产生的误差较大时，系统通过自适应机构改变控制器的参数，使被控对象的输出和参考模型的输出大体一致。因此，模型参考自适应控制具有跟踪迅速的优点，其结构框图如图2所示[12]。

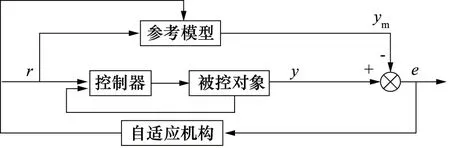
图2 模型参考自适应控制结构框图

设被控对象的状态空间模型为：

(6)

式中，xp(t),u(t) —— 分别为被控对象状态和控制输入

Ap，Bp—— 未知矩阵

参考模型的状态空间模型为：

(7)

式中，xm(t) —— 参考模型状态

Am—— Hurwitz矩阵

Bm—— 已知矩阵

r(t) —— 参考模型激励信号

为了便于分析，作如下两个假设：

(8)

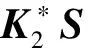
(9)

定义误差信号：

e(t)=xp(t)-xm(t)

(10)

自适应控制律为：

(11)

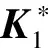
(12)

根据式(7)、式(11)、式(12)，可以推导得出误差系统方程，即：

(13)

2.2 稳定性分析

为了分析控制器的稳定性，可构造的Lyqpunov函数，即：

(14)

式中，Γ1，Γ2均为正定阵。

对式(14)求导，即：

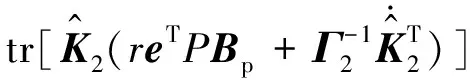
(15)

当式(15)的第二项和第三项均为0时，可得模型参考自适应律，即：

(16)

(17)

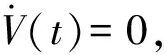
3 基于改进PSO算法的模型参考自适应控制器设计

3.1 改进权重粒子群算法

粒子群算法的基本原理如下：

设D维空间中待优化粒子的总数为m，其可解空间为A={A1,A2,…,AD}，其中的解之一为Ai={A1i,A2i,…,ADi}，每个粒子的速度为Vi={vi1,vi2,…,vid}，根据目标函数来更新解。以下给出待优化粒子的速度和位置更新公式：

(18)

(19)

由式(18)可知，权重系数w和学习因子c1，c2决定着粒子的移动方向。其中，惯性权重w是尤为重要的参数，当w值增大时，算法的全局搜索能力随之提升；若w值减小，则算法的局部搜索能力增强。而传统的粒子群算法虽然容易实现且收敛速度较快，但如果对惯性权重w的值选取不恰当，就很容易导致算法陷入局部最优、收敛速度降低甚至寻优结果不准确等问题。

针对粒子群算法在寻优时出现的上述问题，本研究引进随机权重法改进传统的粒子群算法，以加快其收敛速度，提高其准确性。

惯性权重w的计算公式为：

(20)

式中，N(0,1) —— 标准正态分布的随机数

r—— 0～1之间的随机数

为显示本研究所述算法在参数寻优时的优越性，选取Griewank函数为测试函数，如图3所示，比较传统PSO算法、SAPSO(自适应权重)算法和本研究改进的PSO算法的寻优结果。其中，Griewank函数的表达式为：

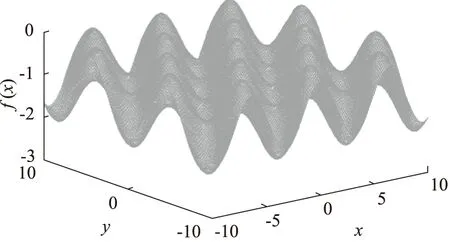
图3 Griewank函数图像

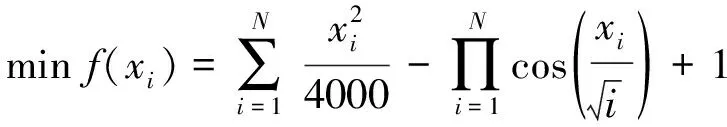
(21)

式中，xi∈[-600,600]。

仿真前，设定粒子数m=100，迭代次数k=40，随机权重平均值的最大值wmax=0.8，随机权重平均值的最小值wmin=0.5，学习因子c1=c2=2，适应度值f。分别对以上3种算法进行仿真分析后，所得的收敛情况如图4所示。

图4 各算法收敛情况对比

对比分析图4可知，SAPSO算法和本研究改进的PSO算法寻优速度和能力优于传统的PSO算法。本研究改进的PSO算法仅在迭代7次后便找到了最优解，寻优效果最好。

3.2 改进PSO算法对模型参考自适应控制器待调整参数的优化

为解决电液位置伺服系统动态性能不佳的问题，本研究将改进的PSO算法应用于模型参考自适应控制器中，并将式(11)中的参数k1，k2加以优化，以提高系统的精度和稳定性。改进PSO算法优化的模型参考自适应控制器流程如下(流程图见图5)：

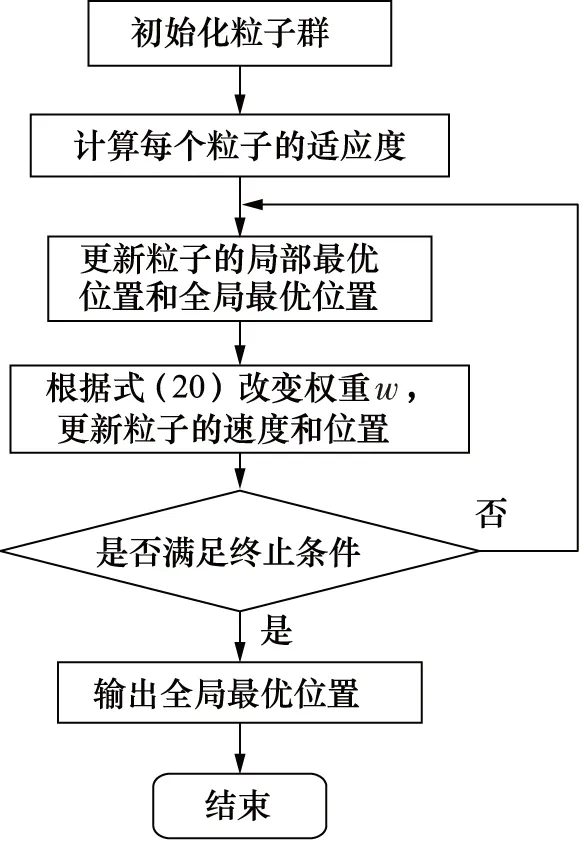
图5 改进PSO算法流程

(1) 初始化粒子群，将各粒子当前局部最优位置Zp设为初始位置，取全局最优位置Zg作为最优值；

(2) 计算每个粒子适应度值，取适应度值最佳的粒子作为新的种群；

(3) 计算当前粒子的速度和位置以更新其局部最优位置和全局最优位置；

(4) 根据式(20)随机选取惯性权重w改变粒子的属性以更新粒子的速度和位置；

(5) 取更新后适应度最佳粒子的最优位置来更新Zg的值；

(6) 当最优值Zg不再变化或迭代次数已达设定值时，终止迭代，程序结束；反之，则返回第(3)步，继续迭代。

4 建模与联合仿真研究

AMESim在液压系统上建模简单且精度高；MATLAB/Simulink能够快速、准确地进行仿真和设计，具有强大的数据处理能力。为使系统的开发更加可靠、实用和方便，本研究选择AMESim/MATLAB联合仿真。

4.1 建模分析

AMESim/MATLAB联合仿真之前，用AMESim软件建立电液位置伺服系统模型，如图6所示。

在AMESim建模仿真时，将电液位置伺服系统中各元器件参数设置为表1所示的数值。为使该系统的控制有较高精度，可通过添加联合仿真接口2与MATLAB/Simulink进行联合仿真。

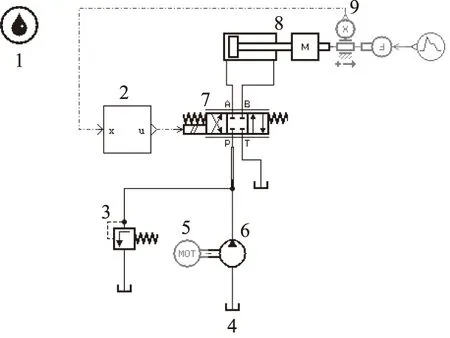
1.油液属性 2.联合仿真接口 3.溢流阀 4.油箱 5.电动机6.液压泵 7.三位四通电液伺服阀 8.液压油缸 9.位移传感器图6 电液位置伺服系统AMESim模型

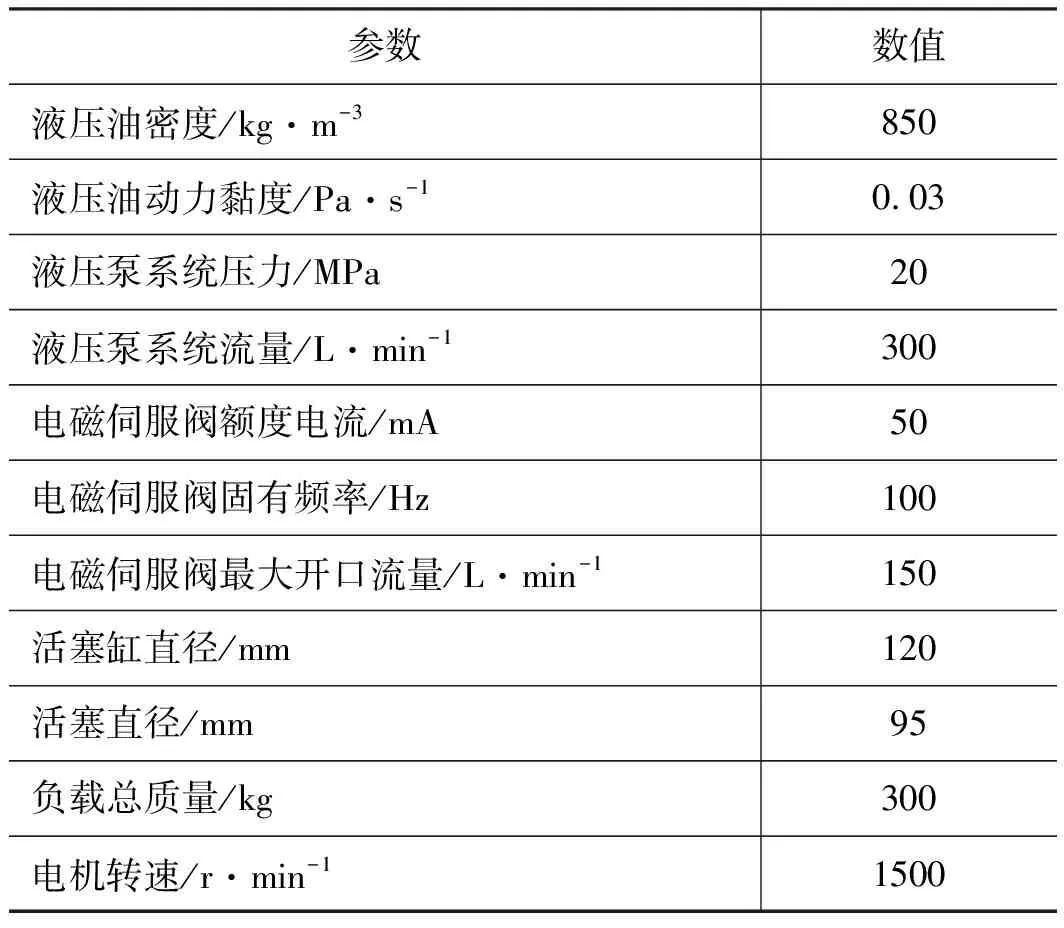
表1 电液位置伺服系统AMESim参数设置

AMESim建模完成后，打开MATLAB中的Simulink模块，并建立如图7所示的电液位置伺服系统Simulink控制模块。图7中，S-Function模块为电液位置伺服系统的AMESim模型；S-Function1模块为导入改进PSO算法后的模型参考自适应控制器；S-Function 2为参考模型的输入。

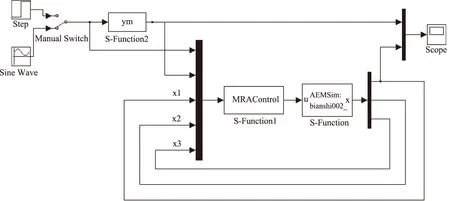
图7 电液位置伺服系统Simulink控制模块

4.2 仿真分析

为了证明本研究提出的改进PSO算法跟踪控制的正确性，向系统提供0.2 null的阶跃信号，仿真时间为30 s，步长为0.01 s，得到系统的位移x跟踪曲线和误差e曲线，其结果如图8所示。

从图8的跟踪曲线和误差曲线可以看出，将改进的PSO算法应用到模型参考自适应控制器中后，系统的跟踪速度较快，在4 s处跟踪到阶跃信号，且位置跟踪误差较小，大约为3%。

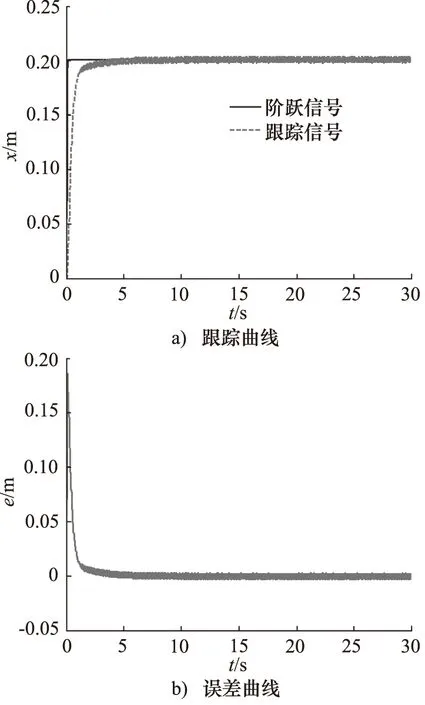
图8 改进PSO优化后的模型参考自适应控制对阶跃信号的跟踪

为了突出本研究提出的改进PSO算法跟踪控制的优越性，向系统提供0.2 null的阶跃信号，仿真的时间为30 s，步长为0.01 s，对比传统PID控制、常规模型参考自适应控制和本研究改进PSO算法优化的模型参考自适应控制的跟踪效果，结果如图9～图11所示。

对比分析图9～图11可知，传统PID控制跟踪精度低，存在滞后现象，误差范围大致在-35～+20 mm之间；常规的模型参考自适应控制跟踪精度高于传统PID控制，且不存在滞后现象，误差范围也有所缩小，大致在±20 mm之间；而相比于常规的模型参考自适应控制和传统的PID控制，本研究提出的改进PSO算法优化后的模型参考自适应控制，不仅解决了滞后延迟问题，而且极大地提高了跟踪精度，误差范围控制在±5 mm之间。

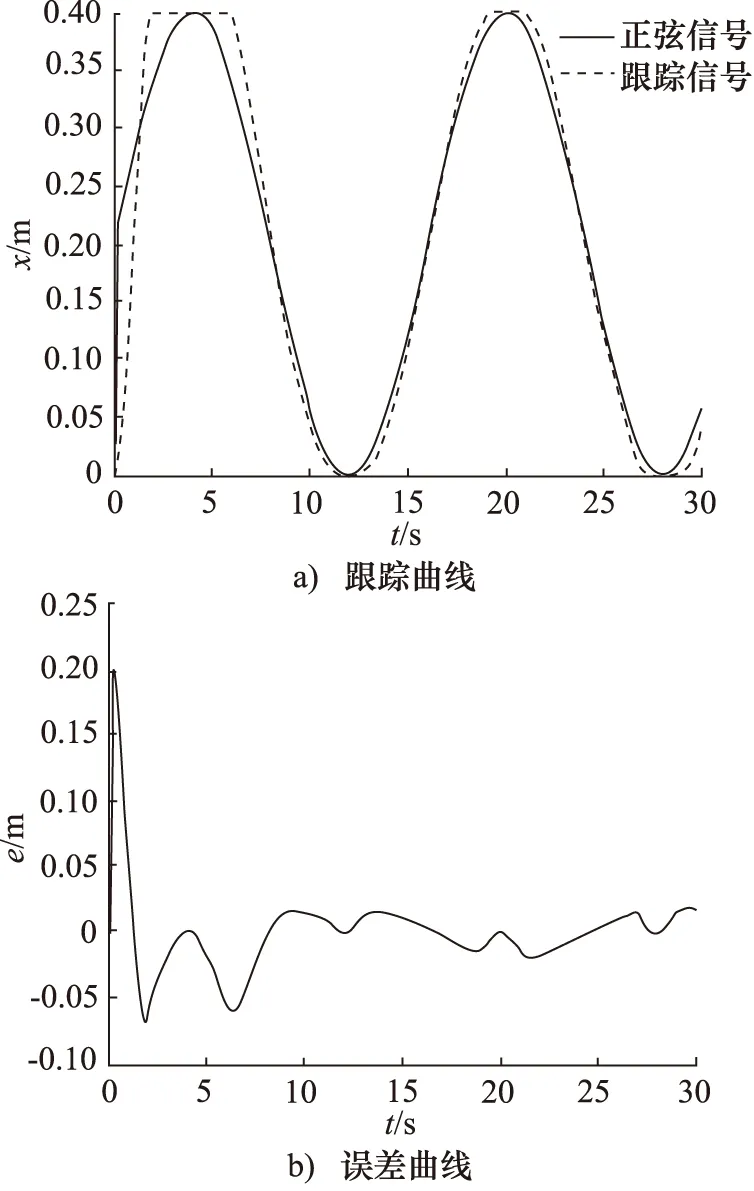
图9 传统PID控制

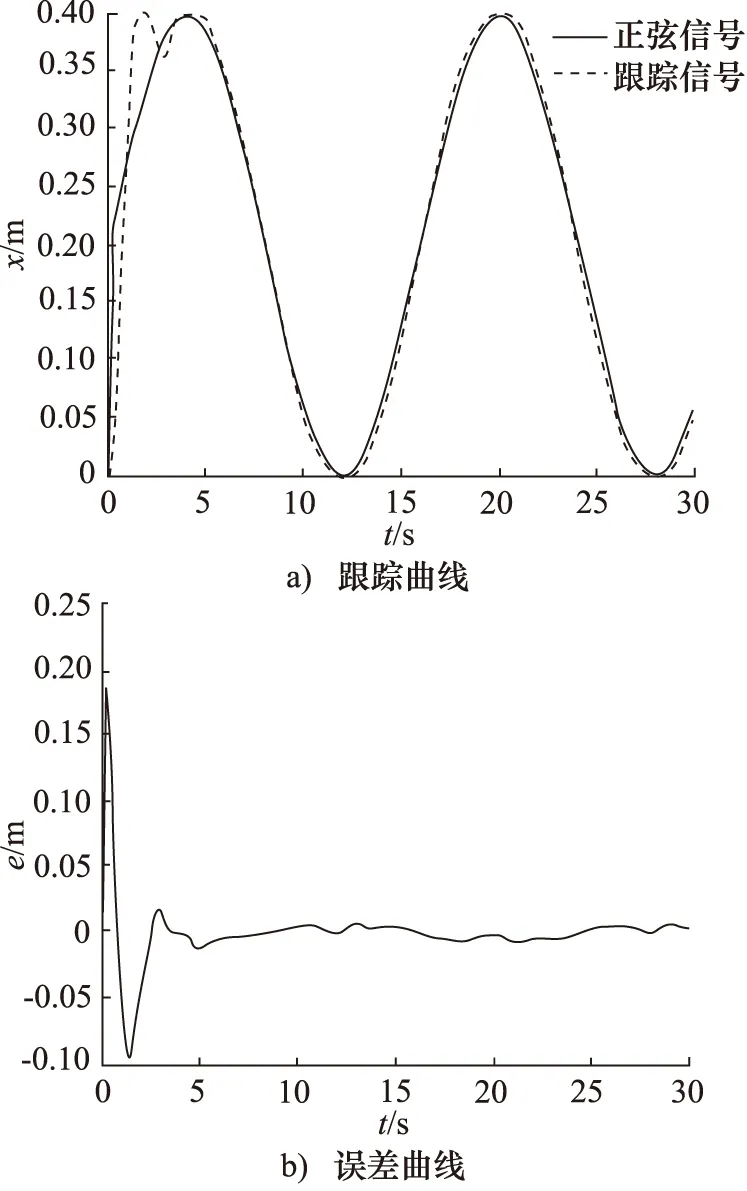
图10 常规模型参考自适应控制

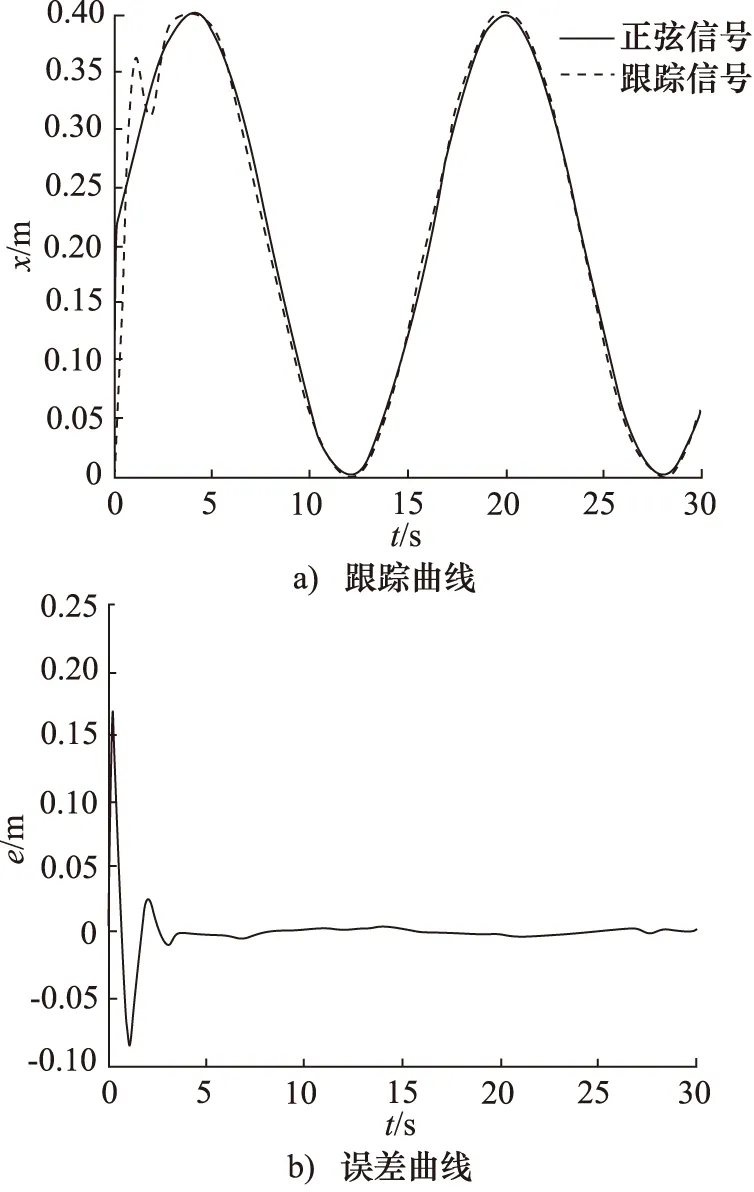
图11 改进PSO优化后的模型参考自适应控制对正弦信号的跟踪

5 结论

(1) 为提高模型参考自适应控制器性能，提出一种改进权重粒子群算法，通过Griewank函数对PSO算法、SAPSO算法和本研究改进PSO算法测试对比，从而验证了本研究所述算法的优越性;

(2) 通过AMESim/MATLAB联合仿真，对比传统PID控制、常规模型参考自适应控制和本研究改进PSO算法优化的模型参考自适应控制的跟踪效果，证明本研究所述方法能更大程度地改善电液位置伺服系统的性能。