放射源处置机器人电液行走控制系统仿真与实验

闫九祥，孙 洁，肖永飞，张艳芳，朱 琳

(齐鲁工业大学(山东省科学院)，山东省科学院自动化研究所，山东省机器人与制造自动化技术重点实验室，山东 济南 250014)

引言

放射源处置机器人适用于核电站事故时放射源装置的无人处置作业，也可用于放射源丢失时，在未知空间内对放射源部件的搜索与回收。通过机器人实现无人作业，提高搜索与处置效率，避免放射源对人员的辐射伤害。

国内外对放射源探测处置机器人运动控制及双马达电液控制技术进行了大量研究，姜明明等[1]设计了一种六轮悬挂移动机器人，该机器人使用三角定位法，对伽马放射源进行搜寻处置。魏晓朝等[2]针对车辆在复杂工作环境下系统负载干扰问题，提出了一种基于液压调速系统的遗传算法优化前馈-反馈+PID转速复合控制方法。张华等[3-4]针对农药喷雾剂液压四驱行走系统，提出直控式复合控制策略及自抗扰控制策略，改善了液压行走机构速度控制性能。丁海港等[5]设计了阀-泵并联变模式液压调速系统，提出了一种并联变模式控制策略，使阀控与泵控协调工作，提高了液压调速系统的灵活性和适应性，丰富了目前液压系统的调速方式。杨前明等[6]、鲁植雄等[7]、郝小星等[8]针对阀控双马达调速系统，分别提出了模糊变结构控制策略、主从式速度同步控制策略及滑膜自适应控制策略等。在研究了相关电液速度控制技术的基础上，结合具体应用需求，重点研究负载时变工况下，双通道电液速度控制问题，以放射源应急处置机器人电液比例阀控马达行走控制系统作为研究对象，建立阀控马达速度控制系统数学模型，提出双通道模糊PID阀控马达转速控制策略，对系统进行仿真与实验，分析验证所设计的电液比例阀控马达行走控制系统的正确性。

1 电液行走控制系统概述

图1为放射源处置机器人结构示意图，机器人由6部分组成。放射源探测器可探测一定空间范围内的放射源信号，同时输出放射源相对机器人的三维空间坐标信息，行走机构将放射源坐标位置信息作为寻源目标，进行自动或遥操寻源作业。放射源应急处置机器人设计有柔性机械臂、液压机械臂进行放射源的处置作业。液压机械臂可配置不同类型的执行机构进行障碍物破拆与重物搬移，柔性机械臂采用直流伺服电机驱动，可进行高精度微操作业。在放射源处置作业时，机器人通过监控系统为手动遥操作业回传实时现场画面。

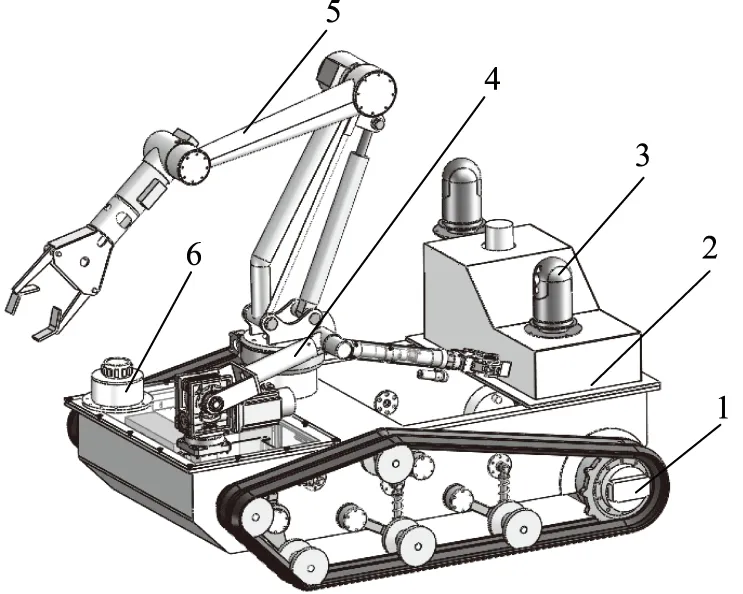
1.行走机构 2.机身本体 3.监控系统 4.柔性机械臂5.液压机械臂 6.放射源探测器图1 放射源处置机器人结构示意图

图2为放射源应急处置机器人电液行走控制系统原理图，电液行走控制系统主要由控制器、液压泵、比例换向阀、液压马达、转速传感器等组成。给定控制器初始电信号值，控制器对给定电信号进行计算处理并输出PWM电流信号驱动电液比例换向阀，电液比例换向阀阀芯位移根据驱动电流信号变化，从而改变进入液压马达的液压油流量，控制液压马达的转速。在液压马达处加装速度编码器，采集马达转速并与给定的电信号进行比较处理，所得的信号差值作为二次控制调节信号，对液压马达速度进行调节。

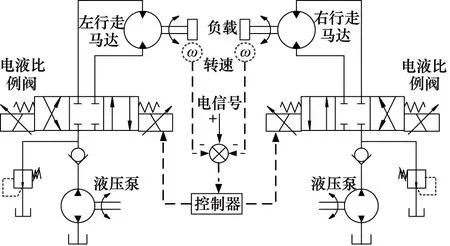
图2 机器人电液行走控制系统原理图

2 电液控制系统数学建模

2.1 系统模型数学方程

换向阀的线性化流量方程为[8]：

(1)

式中，QL1,QL2—— 左右滑阀负载流量

Kq1，Kq2—— 左右滑阀流量增益

Xv1，Xv2—— 左右滑阀位移

Kc1，Kc2—— 左右滑阀流量压力系数

pL1，pL2—— 左右液压负载压力

假定本系统中各阀与马达连接油管短而粗，忽略管路的内摩擦力，且系统无饱和及气穴现象，液压油温度及体积弹性模量恒定，则马达腔流量连续方程为[9]：

(2)

式中，Qm1，Qm2—— 左右马达负载流量

Dm1，Dm2—— 左右马达弧度排量

θ1，θ2—— 左右马达角位移

Cm1，Cm2—— 左右马达泄漏系数

Vm1，Vm2—— 左右马达有效容积

βe—— 马达体积弹性模量

在不考虑液压油质量的前提下，根据牛顿力学定律，液压马达的力矩平衡方程为[10]：

(3)

式中,J1，J2—— 左右马达负载等效转动惯量

Bm1，Bm2—— 左右马达负载阻尼系数

K1，K2—— 左右马达负载弹簧刚度

T1，T2—— 左右马达等效总力矩

2.2 系统传递函数

图3为机器人电液行走控制系统传递函数框图。G11(S),G12(S),G13(S),G14(S)分别为左行走机构控制器模块、PWM电流模块、比例换向阀、液压马达的传递函数，G21(S),G22(S),G23(S),G24(S)分别为右行走机构控制器模块、PWM电流模块、比例换向阀、液压马达的传递函数。滑阀固有频率与液压固有频率接近，行走机构外力负载为履带与地面摩擦力，对式(1)～式(3)进行拉氏变换，得到电液比例阀及液压马达与负载的传递函数，控制器、速度传感器的传递函数参数由元件出厂设定参数确定。

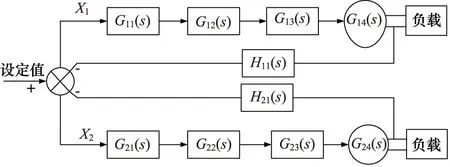
图3 机器人电液行走控制系统传递函数框图

系统中各元件所对应的传递函数串联组成机器人电液比例行走控制系统的传递函数，系统各环节传递函数为：

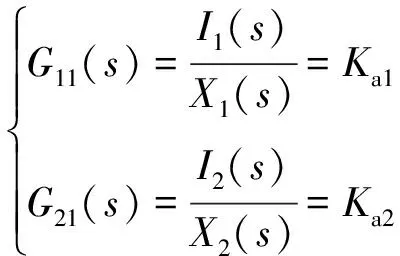
(4)

(5)

(6)

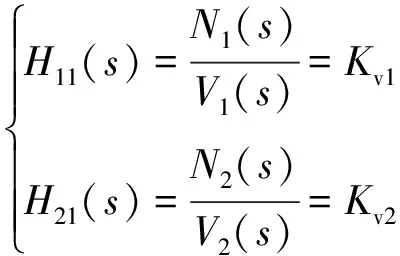
(7)

式中，I1(s)，I2(s) —— 左右通道输出电流

X1(s)，X2(s) —— 系统左右通道输入值

Ka1，Ka2—— 左右通道比例环节增益

Q1(s)，Q2(s) —— 左右通道比例阀空载流量

ωsv1，ωsv2—— 左右通道比例阀固有频率

ξ1，ξ2—— 比例阀阻尼比

ωh1，ωh2—— 左右通道液压马达固有频率

N1(s)，N2(s) —— 左右通道速度传感器脉冲数

V1(s)，V2(s) —— 左右通道马达输出轴转速

Kv1，Kv2—— 左右通道速度传感器增益[11]

2.3 控制策略及系统模型

放射源应急处置机器人寻源行走过程中，控制器根据接收到的放射源位置信息及空间位置导航信息计算双马达输出速度，同时监测双马达转速反馈值，对输出转速进行实时调整，实现机器人差速转向、直线行驶。由于作业空间及行驶环境复杂多变，系统须具备自适应调整功能，同时对输入信号具备高速、高精度响应。

在典型时域线性控制系统采用的经典PID控制器，通过对控制器比例、积分、微分参数的整定，使控制系统响应速度提高，动态性能改善，消除稳态误差[12-13]。放射源应急处置机器人电液行走控制系统在实际工作环境中，行驶负载存在时变性，负载的变化会产生功率损耗，经典PID控制策略无法满足系统的时变控制[14-15]。为实现系统控制目标，提出双通道模糊PID控制策略，机器人电液行走模糊PID控制系统模型如图4所示。在不同负载条件下测试液压马达的速度与加速度，对PID控制器参数进行整定，得到不同负载条件下最优参数集，模糊规律如表1所示，表中a，b，c分别代表参量ΔKp，ΔKi，ΔKd。

表1 ΔKp，ΔKi，ΔKd模糊规律

图4 机器人电液行走控制系统模型

3 系统仿真与实验

3.1 建立系统Simulink仿真模型

放射源应急处置机器人电液行走控制系统的电液比例换向阀及液压马达参数如表2所示。根据机器人电液行走控制系统闭环传递函数方框图，在MATLAB仿真软件中建立系统仿真模型，将表2所示液压系统参数带入控制系统闭环传递函数模型中，在控制模型中引入模糊PID控制器，在MATLAB仿真软件中对系统仿真模型输入幅值为1的阶跃信号，仿真运行4 s，仿真系统函数对阶跃信号的时域响应，将仿真结果输出到图形显示元件中。

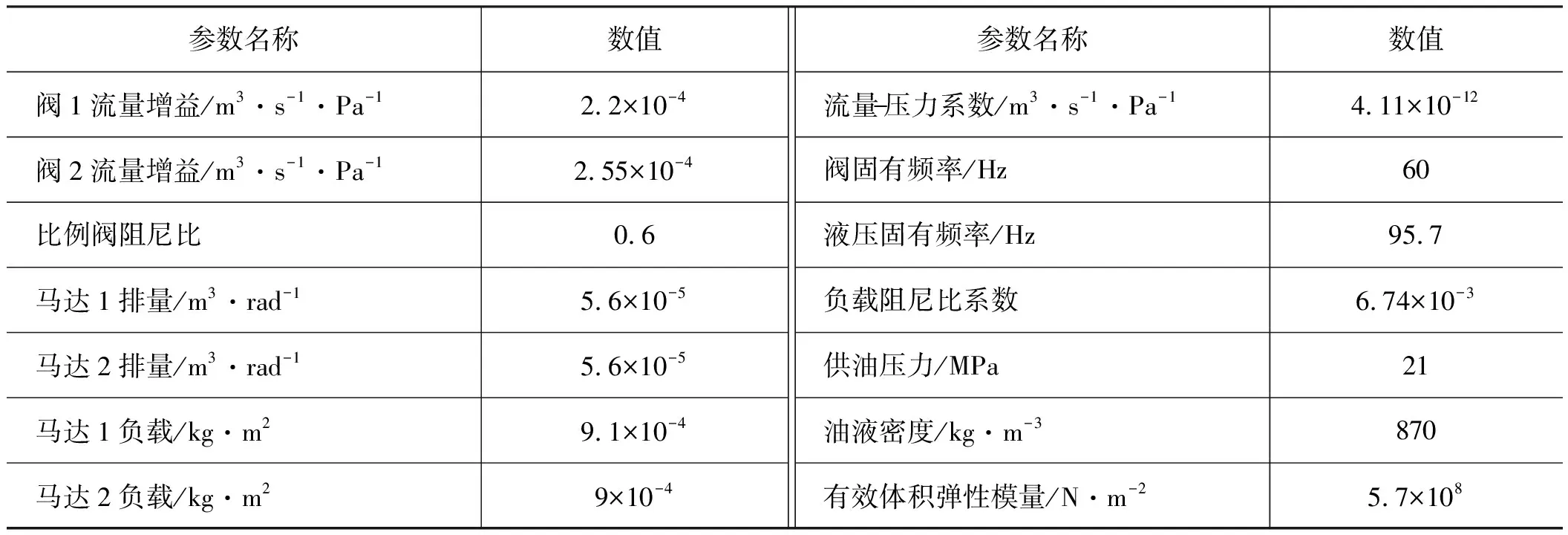
表2 液压系统参数

3.2 系统仿真分析

将元件参数带入放射源应急处置机器人双马达电液比例阀控马达行走控制系统数学模型中，对系统模型进行仿真，分析系统动态特性，验证所设计的行走驱动控制系统的正确性。

对无PID矫正系统输入幅值为1的阶跃响应信号ω，仿真时间4 s，在系统模型中引入模糊PID控制器，仿真结果如图5所示。系统要求机器人行走系统对行进与制动2个工况的行驶响应都具备优良的动态响应特性，对系统输入周期性脉冲跟随方波进行仿真，验证系统行进与制动运动时控制系统输出性能，系统响应输出如图6所示。

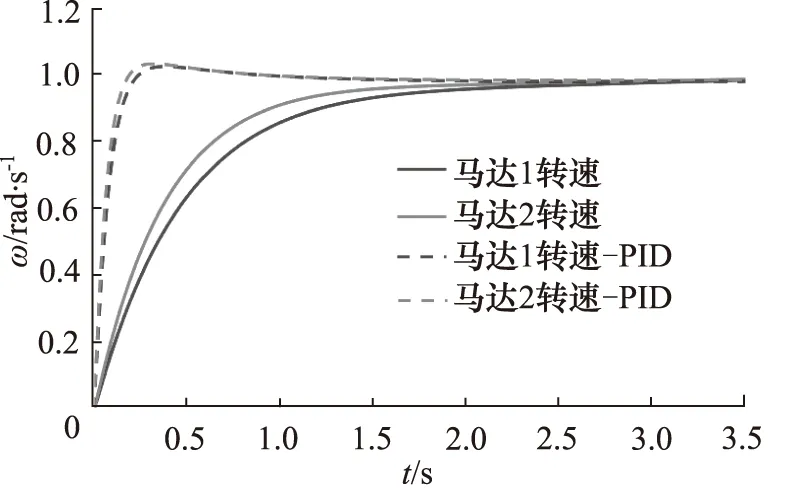
图5 系统阶跃响应时域曲线

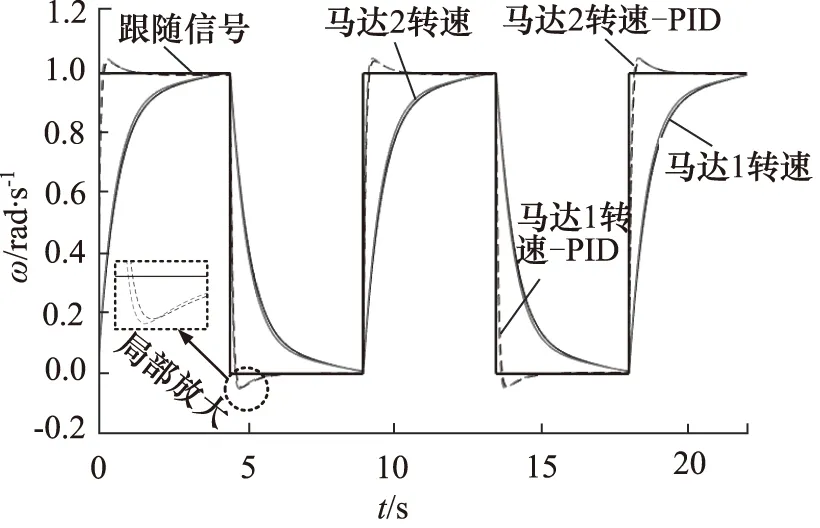
图6 系统阶跃响应跟随曲线

对比无矫正系统和模糊PID控制器矫正系统的仿真曲线图5及系统阶跃响应跟随曲线图6，可以看出：

(1) 无矫正系统在阶跃信号的触发下，时域输出曲线在3 s后达到稳态输出，无超调。双侧行走马达在1.5 s前最大速度响应差值为输入信号幅值的15%；

(2) 模糊PID矫正后系统响应速度提高，在1.3 s时达到稳态输出，双侧行走马达在0.3 s前最大速度响应差值为输入信号幅值的3%；

(3) PID矫正后系在周期阶跃信号的触发下，双侧行走马达加减速响应输出最大速度响应差值均低于输入信号幅值的3%。

仿真结果表明，无矫正系统时域输出曲线可达到稳态输出，稳态误差较小，无超调，证明了所推导的数学模型的正确性。

系统无矫正前双侧行走马达在1.5 s前最大速度响应差值为输入信号幅值的15%，无法满足高速直线行走及快速转向的要求。模糊PID矫正后系统稳态响应时间提高到1.3 s，双侧行走马达在0.3 s前最大速度响应最大差值降低为输入信号幅值的3%，改善了系统动态响应性能。

双侧行走马达加减速响应时间均明显提高，达到稳态输出前双侧马达速度差值均低于输入信号幅值的3%，PID矫正后系统做行进与制动运动时，均具有较好的动态输出特性。

3.3 系统实验分析

进行实验的机器人样机如图7所示，电液行走控制系统由液压泵、液压马达、电液比例换向阀、控制器等组成，液压马达输出轴安装有SICK编码器，液压泵由直流伺服电机驱动。液压泵采用A1V18定量泵，液压马达选用JT02VN，电液比例阀为4WRAE系列，所需输入电流范围为0～1 A；控制器采用EPEC3036，该控制器可编程输出PWM电流范围为0～1.03 A，分辨率为1 mA;控制器通过CAN总线接收速度传感器数据。

图7 实验机器人样机实物图

如图8所示，选用实验场地为不平整砂石路面，在这种路面条件下，机器人在行走时所克服的行走阻力随路面起伏变化。为验证电液行走控制系统动态性能，在控制器中对系统加载匀加速、匀速、匀减速三段式速度运动曲线，验证系统在不平整砂石路面条件下对不同运动条件的输出响应。

图8 实验现场

三段式速度运动曲线如图9所示，匀加速阶段加速度为1.5 rad/s2，匀速阶段速度为3 rad/s，匀减速阶段加速度为0.75 rad/s2。通过采集双侧编码器速度反馈值绘制双马达转速响应曲线，如图10所示。

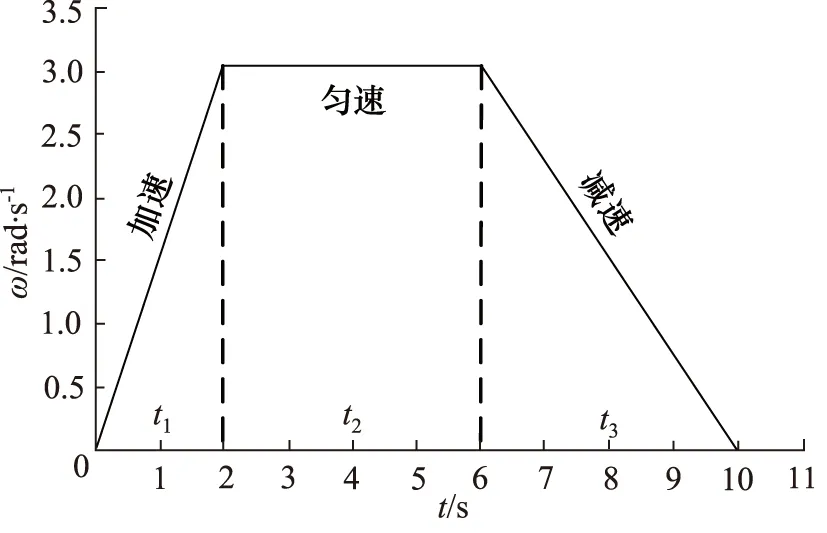
图9 三段式速度输入曲线

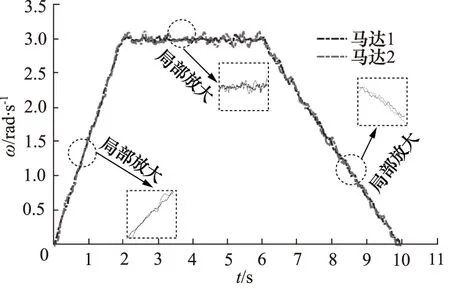
图10 马达转速实验结果拟合曲线

实验结果表明，在不平整砂石路面情况下，双侧马达转在加减速阶段最大转速稳态误差低于幅值2%，在匀速行走阶段，最大转速稳态误差低于幅值3%，试验结果与仿真结果吻合，验证了控制模型的正确性。所采集的马达速度响应值对输入曲线的拟合优度为0.96，试验结果证明了系统在加速、匀速及减速度阶段具有良好的响应特性。

4 结论

利用MATLAB仿真工具对所设计的模糊PID控制系统模型进行仿真验证，仿真结果表明，系统响应速度提高至1.3 s，速度差值低于输入幅值3%，稳定精度得到改善。通过样机在负载砂石路面的三段速度行走实验，证明了建立的阀控马达速度控制系统数学模型及双通道模糊PID电液比例速度控制策略的正确性及准确性。仿真及实验结果证明所设计的全液压履带式电液比例阀控双液压马达行走控制系统方案可以满足放射源处置机器人对电液行走机构的速度性能要求。