微型高速轴向柱塞泵动力学特性分析
2021-11-02叶绍干卜祥建赵守军刘会祥
叶绍干,李 旭,侯 亮,卜祥建,赵守军,刘会祥
(1.厦门大学 机电工程系,福建 厦门 361021;2.浙江大学 流体动力与机电系统国家重点实验室,浙江 杭州 310027;3.北京精密机电控制设备研究所,北京 100076)
引言
作为斜盘式的微型高速轴向柱塞泵具有结构紧凑和流量大等特点,是液压系统高功率密度动力源最广泛的选择对象[1]。高速下柱塞泵的主轴与缸体常伴随着振动、倾覆和质心轨迹不对中等问题,对柱塞泵的工作性能和使用寿命具有重大影响[2]。
针对柱塞泵转子系统动力学特性,CAO Hongrui等[3]建立了考虑轴承滚子等效弹簧阻尼单元的转子-轴承座系统的动力学模型,研究了转子系统动力学特性;CHEN G[4]建立了一种新的转子-球轴承-定子耦合系统动力学模型,用于模拟实际的航空发动机整机振动。针对柱塞泵多体系统动力学特性,MILIND T R等[5]提出了一种多体动力学和有限元相结合的方法来模拟轴向柱塞泵的动力学和振动特性;CHEN H X等[6]建立了具有3个质量和14个自由度斜盘式水压马达的理论动力学模型,在该模型中,主要部件通过与弹簧-阻尼单元连接的多个集中质量点进行简化,通过数值模拟研究了水压活塞马达的一系列动态振动特性;在此发展基础之上,YE Shaogan等[7-8]建立了具有4个质量和19个自由度轴向柱塞泵的理论动力学模型,实验并验证了动力学模型,分析了工况条件对柱塞泵振动特性的影响。
综上所述,本研究通过建立柱塞泵的动力学模型,分析不同工况下主轴与缸体的振动响应和质心轨迹,研究微型高速轴向柱塞泵的动力学特性。
1 柱塞泵动力学模型
本研究对象为微型高速斜盘式定量轴向柱塞泵,其结构如图1所示。柱塞泵主要组成部件包括壳体、端盖、斜盘、柱塞、回程盘、滑靴、缸体、配流盘、轴承和主轴。

图1 微型高速轴向柱塞泵模型Fig.1 Micro high-speed axial piston pump model
轴向柱塞泵各零部件约束类型包括固定类型和运动类型。其中固定类型的约束包括: 缸体与主轴、主轴与电机联轴器花键固定,壳体与端盖、壳体与固定位置螺栓固定,壳体与斜盘通过销钉固定,配流盘与端盖通过圆柱销固定。运动类型的约束包括:柱塞在缸体柱塞腔内的往复直线运动,滑靴在斜盘上的平面运动及与柱塞球头的旋转运动等。柱塞泵受力的主要组成:主轴缸体弹簧预压力,各个柱塞腔油液冲击压力。
柱塞泵运动部件之间会形成柱塞副、配流副和滑靴副。这3对重要的摩擦副之间形成油膜,油膜对部件有支撑和润滑作用,对微型高速轴向柱塞泵的动力学特性具有重要影响[9]。
1.1 动力学模型描述
首先,对柱塞泵部件复杂的约束和连接类型等进行简化。本研究对动力学模型做了如下简化[6]:
(1) 各部件被简化成集中质量模型,在平移和转动方向上具有相应的质量和转动惯量;
(2) 通过X,Y,Z方向的平动和转动刚度等效简化轴向柱塞泵各零部件约束[10];
(3) 通过创建无质量的弹簧-阻尼单元等效3对摩擦副之间油膜复杂的作用形式,轴承采用线性刚度模型进行建模,并用弹簧-阻尼单元等效轴承;
(4) 将螺栓简化为弹簧,在X,Y,Z3个方向刚度分别为5.2×108N/m,5.2×108N/m和1.1×108N/m。
动力学简化模型如图2所示,Kp和Cp为缸体与柱塞之间相互作用的油膜等效弹簧-阻尼单元;Kvp和Cvp为缸体与配流盘之间相互作用的油膜等效弹簧-阻尼单元;Rcv为作用在配流盘上的4个等效弹簧-阻尼单元圆周分布半径;Ks和Cs为滑靴与斜盘之间相互作用的油膜等效弹簧-阻尼单元;Ksh1和Csh1为端盖与主轴处支撑轴承的等效刚度-阻尼单元;Ksh2和Csh2分别表示为壳体与主轴处支撑轴承的等效刚度-阻尼单元;考虑柱塞存在绕其轴向的转动阻尼力,参考值为500 N·m·s/rad,系数取值如表1所示[6-8]。
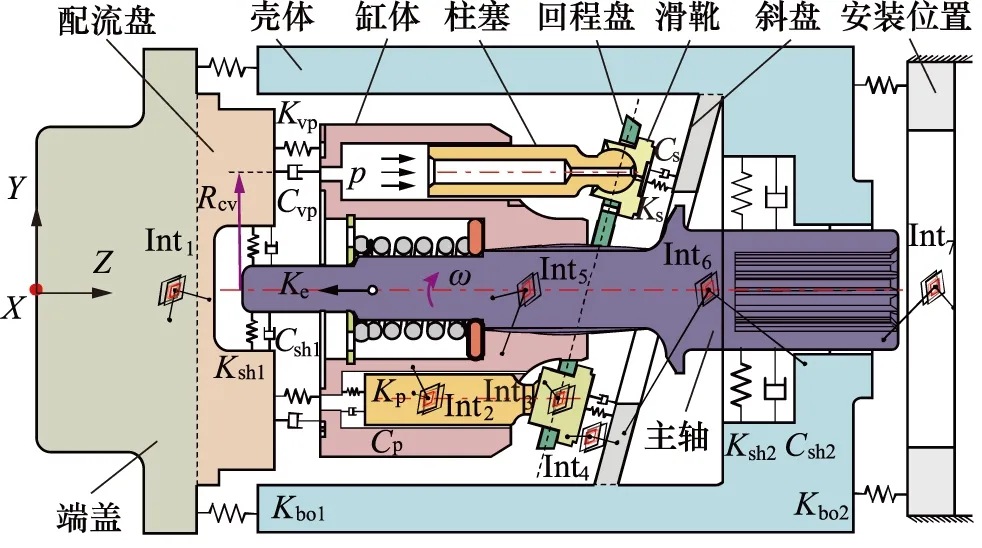
图2 微型高速轴向柱塞泵多体动力学示意图

表1 弹簧-阻尼单元系数Tab.1 Spring-damping element coefficient
Int1表示部件端盖和配流盘的约束关系;Int2表示部件柱塞和缸体往复直线运动约束关系;Int3表示滑靴和柱塞球头旋转运动约束关系;Int4表示滑靴和斜盘平面运动约束关系;Int5表示缸体和主轴固定约束关系;Int6表示壳体和斜盘固定约束关系;Int7表示主轴和电机联轴器固定约束关系,部件平动和转动方向的约束刚度值如表2所示。
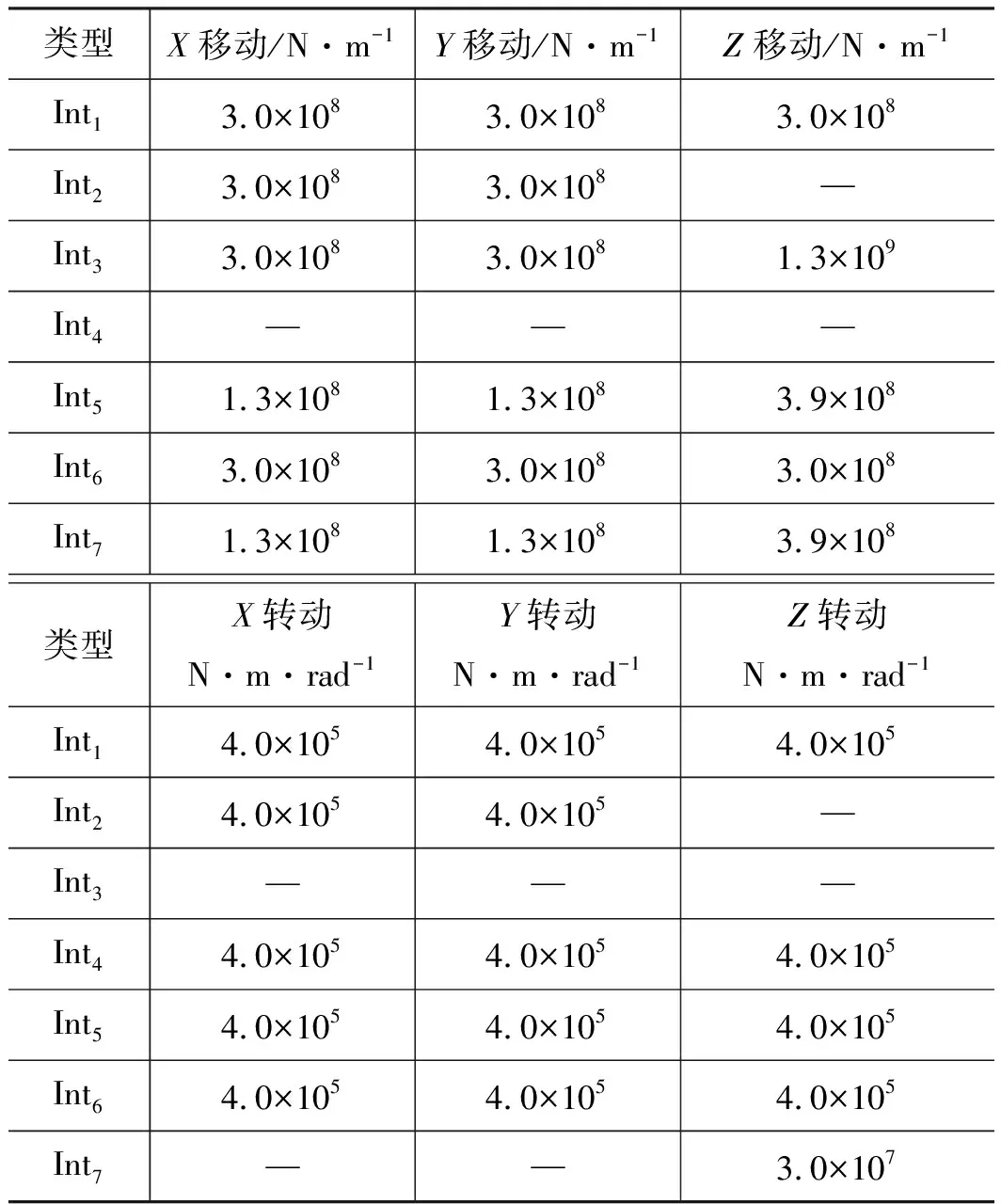
表2 部件约束刚度Tab.2 Restraint stiffness of components
Kbo1和Kbo2分别表示为连接壳体与端盖,壳体与安装位置的螺栓等效刚度,由螺栓尺寸和规格决定。Ke为主轴缸体弹簧刚度,可由经验式(1)计算:
(1)
式中,G—— 剪切模量
d—— 线径
n—— 弹簧有效圈数
D—— 弹簧中心直径
1.2 柱塞腔压力求解
柱塞腔压力作为主要的柱塞泵外力输入到动力学模型中,对分析柱塞泵动力学特性具有重要的影响,因此,柱塞腔压力的求解是柱塞泵动力学建模的关键。由于柱塞腔压力的测量需要耗费较高的成本,工程实践中通常使用集总参数法或三维计算流体动力学(CFD)法来实现柱塞腔压力的求解[11-13]。
首先,确定如表3所示的微型高速轴向柱塞泵的主要参数;其次,分别建立其柱塞副模型、配流副模型和滑靴副模型;然后,将各个模型联立求得柱塞腔压力;最后,将柱塞腔压力求解结果作为外力输入到柱塞泵多体系统动力学模型中,建立柱塞泵液固耦合动力学模型[14-16]。
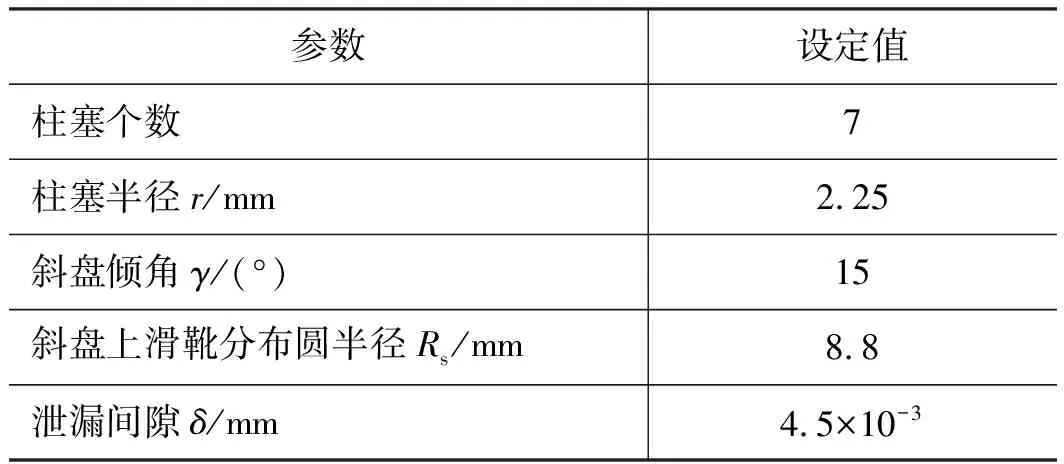
表3 主要参数Tab.3 Main parameters
图3a为柱塞副模型,由于半径为r的柱塞在缸体内往复直线运动会改变柱塞腔容积大小,柱塞腔容积变化导致其压力变化,考虑柱塞腔油液在柱塞缸体间隙和柱塞滑靴阻尼孔产生泄漏量Q,该模型用泄漏间隙δ模拟最终柱塞缸体和柱塞滑靴之间的泄漏量[17-19]。
图3b为滑靴副模型,其中,斜盘上滑靴分度圆半径为Rs,滑靴在固定斜盘表面做圆周运动,通过旋转变直线的方式求得柱塞滑靴位置的变化量dh随时间的变化函数关系和初始位置h0,求出柱塞滑靴位置关于时间的变化曲线。
图3c为配流副模型,由于油液由柱塞腔流经配流盘腰形槽进油口A1和排油口A2时过流面积的改变,柱塞腔压力p在缸体柱塞旋转运动过程中随时间变化。根据配流盘结构,可以测得柱塞腔宽度半径、配流盘腰形槽半径、柱塞腔线性长度和交互边界角度。然后,建立单个柱塞腔流经配流盘腰形槽的交互面积分段函数,求出过流面积关于时间的变化曲线[19-20]。

图3 液压模型示意图Fig.3 Schematic diagram of hydraulic model
2 振动响应分析
2.1 振动位移频谱分析
对柱塞泵动力学模型得到主轴与缸体时域下的振动位移和倾覆角度结果进行傅里叶变换,分析5000 Hz内的振动响应频谱结果。计算3种转速下主轴与缸体的基频分别为300,333,383 Hz。
图4为柱塞泵工作压力为21 MPa不同转速下主轴在X,Y,Z方向的振动位移频谱,图中1×表示为相应转速下基频,2×,3×,…表示其谐波。主轴X方向振动位移峰值在1×和2×处,且2×处峰值最大;主轴Y方向振动位移峰值在1×,2×,4×,6×,8×,10×,12×和14×处,且2×处峰值最大;主轴Z方向振动位移峰值在2×,7×,8×,10×,12×和14×处,且2×处峰值较大,但是转速为23000 r/min时12×处振动位移峰值最大。

图4 21 MPa时主轴振动位移频谱Fig.4 Vibration displacement spectrum of shaft at 21 MPa
图5为柱塞泵转速为20000 r/min不同压力下主轴在X,Y,Z方向的振动位移频谱。随着柱塞泵压力升高,主轴X和Y方向上振动位移幅值在2×处均增大;同时,主轴Z方向上振动位移幅值在2×和7×处均增大。但是,12×和14×处主轴Y和Z方向上振动位移幅值最大时对应的压力分别为21 MPa和14 MPa。

图5 20000 r/min时主轴振动位移频谱Fig.5 Vibration displacement spectrum of shaft at 20000 r/min
图6为柱塞泵工作压力为21 MPa不同转速下缸体在X,Y,Z方向的振动位移频谱。缸体X方向振动位移峰值在1×,2×和4×处,且2×处峰值最大;缸体Y方向振动位移峰值在1×,2×,4×,6×,8×,10×,12×和14×处,且2×处峰值最大;缸体Z方向振动位移峰值在2×,7×,8×,10×,12×和14×处,且2×处峰值较大,但是转速为23000 r/min时12×处振动位移峰值最大。

图6 21 MPa时缸体振动位移频谱Fig.6 Vibration displacement spectrum of cylinder at 21 MPa
图7为柱塞泵转速为20000 r/min不同压力下缸体在X,Y,Z方向的振动位移频谱。随着柱塞泵压力升高,缸体X和Y方向上振动位移幅值在2×处均增大,缸体Z方向上振动位移幅值在2×和7×处均增大。但是,12×和14×处缸体Y和Z方向上振动位移幅值最大时对应的压力分别为21 MPa和14 MPa。
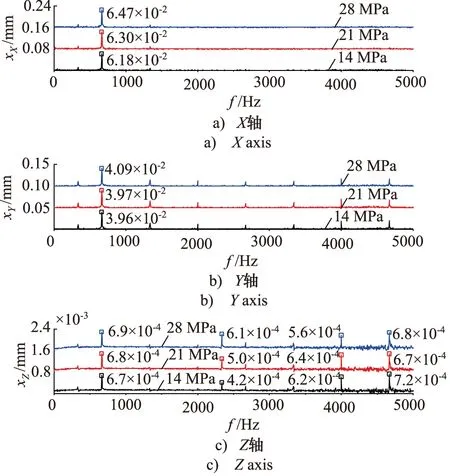
图7 20000 r/min时缸体振动位移频谱Fig.7 Vibration displacement spectrum of cylinder at 20000 r/min
主轴与缸体的振动位移峰值在其偶倍频处较大,部分谐波振动位移幅值会随着压力的增大而增大;相同工况下的缸体振动位移幅值大于主轴振动位移幅值。
2.2 倾覆角度频谱分析
高速工况下旋转部件的倾覆加剧,造成泄漏流量增大和部件磨损,影响柱塞泵的性能[2]。图8为柱塞泵工作压力为21 MPa不同转速下主轴绕X轴和Y轴的倾覆角度频谱。主轴绕X轴的倾覆角度θX峰值在1×,2×,3×,5×,7×,9×,11×和13×处,且1×处峰值最大;主轴绕Y轴的倾覆角度θY峰值在1×,2×和3×处,且1×处峰值最大。

图8 21 MPa时主轴倾覆角度频谱Fig.8 Overturning angle spectrum of shaft at 21 MPa
图9为柱塞泵转速为20000 r/min不同压力下主轴绕X轴和Y轴的倾覆角度频谱。随着柱塞泵压力升高,主轴绕X轴的倾覆角度幅值在3×处增大,在1×处减小;主轴绕Y轴的倾覆角度幅值在1×处增大。

图9 20000 r/min时主轴倾覆角度频谱Fig.9 Overturning angle spectrum of shaft at 20000 r/min
图10为柱塞泵工作压力为21 MPa不同转速下缸体绕X轴和Y轴的倾覆角度频谱。缸体绕X轴的倾覆角度峰值在1×,2×,3×,5×,7×,9×,11×和13×处,且1×处峰值最大;缸体绕Y轴的倾覆角度峰值在1×,2×和3×处,且1×处峰值最大。
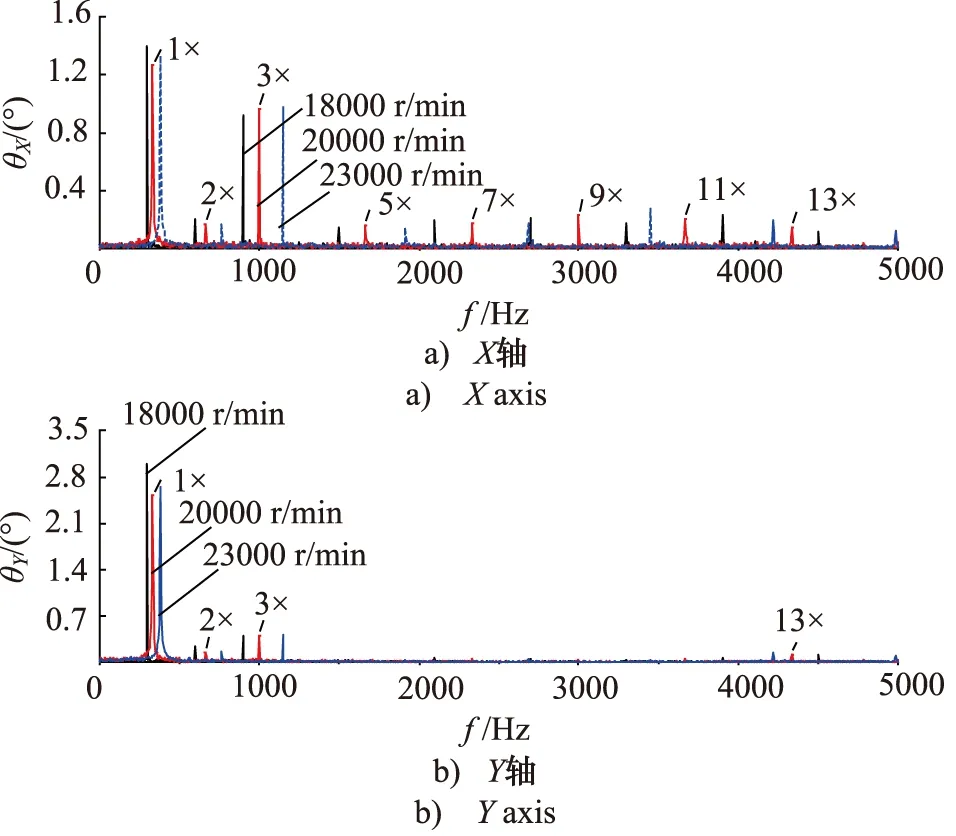
图10 21 MPa时缸体倾覆角度频谱Fig.10 Overturning angle spectrum of cylinder at 21 MPa
图11为柱塞泵转速为20000 r/min不同压力下缸体绕X轴和Y轴的倾覆角度频谱。随着柱塞泵压力升高,缸体绕X轴的倾覆角度幅值在3×处增大,在1× 处减小;缸体绕Y轴的倾覆角度幅值在1×处增大。

图11 20000 r/min时缸体倾覆角度频谱Fig.11 Overturning angle spectrum of cylinder at 20000 r/min
主轴与缸体的倾覆角度幅值峰值在其奇倍频处,部分谐波倾覆角度幅值会随着压力的增大而增大。
3 质心轨迹分析
3.1 主轴
柱塞泵旋转组件的质心运动轨迹影响着柱塞泵的性能,对开展柱塞泵动力学特性分析有着十分重要的影响。
图12为21 MPa不同转速下主轴的质心轨迹曲线。主轴质心始终在X和Y的负半轴形成扇叶形的运动轨迹;同时,随着转速的升高,主轴质心运动轨迹形成不规整的3片扇叶,且整体向Y负半轴移动;当转速为23000 r/min时,右下扇叶小范围出现突起。

图12 21 MPa时主轴质心轨迹Fig.12 Centroid trajectory of shaft at 21 MPa
图13为20000 r/min不同压力下主轴的质心轨迹曲线。随着柱塞泵压力升高,主轴质心运动轨迹保持扇叶形状,扇叶的每个叶片的面积减小。

图13 20000 r/min时主轴质心轨迹Fig.13 Centroid trajectory of shaft at 20000 r/min
3.2 缸体
图14为21 MPa不同转速下缸体的质心轨迹曲线。缸体质心始终在X和Y的负半轴形成扇叶形的运动轨迹;同时,随着转速的升高,缸体质心运动轨迹形成类似主轴质心轨迹定义的扇叶形,且整体向Y负半轴移动;当转速为23000 r/min时,右下扇叶小范围出现突起。
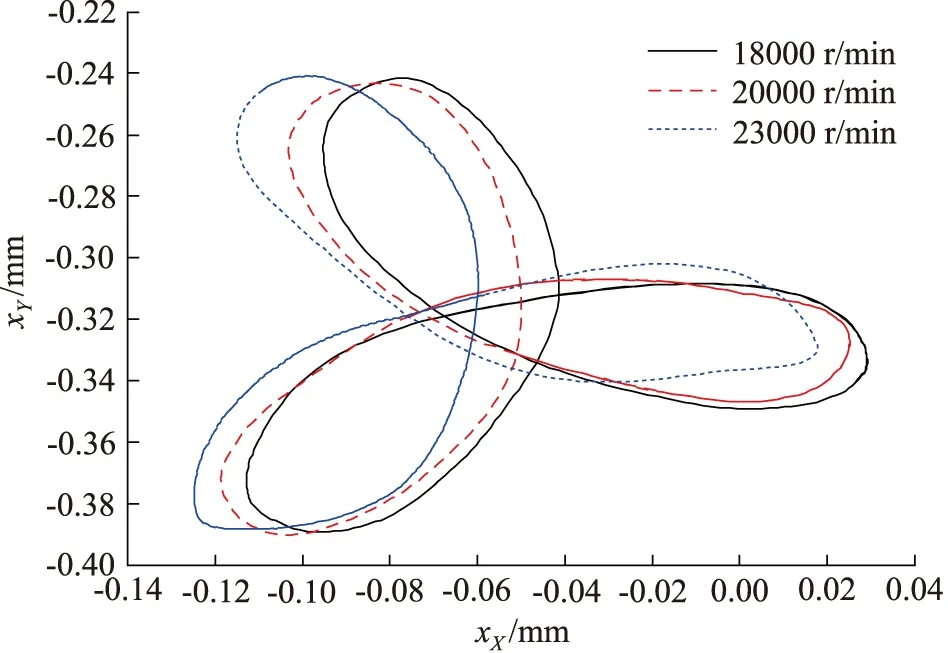
图14 21 MPa时缸体质心轨迹Fig.14 Centroid trajectory of cylinder at 21 MPa
图15为20000 r/min不同压力下缸体的质心轨迹曲线。随着柱塞泵压力升高,缸体质心运动轨迹保持扇叶形状,扇叶的每个叶片的面积减小。对比图13与图15可知,缸体与主轴质心轨迹为3片扇叶形状,其不规则的程度会随着转速的增大而增大,且整体向Y负半轴移动;同时,扇叶的面积会随着压力的增大而减小。
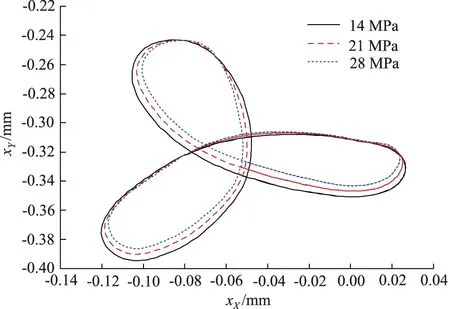
图15 20000 r/min时缸体质心轨迹Fig.15 Centroid trajectory of cylinder at 20000 r/min
4 结论
本研究建立了微型高速轴向柱塞泵的动力学模型,分析了不同工况下主轴与缸体的振动响应和质心轨迹的特性。得出以下结论:
(1) 主轴与缸体的X方向振动位移峰值在1×和2×处,且2×处峰值最大;Y方向振动位移峰值在1×及其偶倍频处,且2×处峰值最大;Z方向振动位移峰值在2×,7×,8×,10×,12×和14×倍频处,且2×处峰值较大,但是转速为23000 r/min时12×处峰值最大。主轴与缸体绕X轴的倾覆角度峰值在2×及其奇倍频处;绕Y轴的倾覆角度峰值在1×,2×和3×倍频处,均在1×处峰值最大。部分谐波振动位移和倾覆角度幅值会随着压力的增大而增大;
(2) 主轴与缸体的质心轨迹呈扇叶形状,质心轨迹形状不规则程度会随着转速的增大而增大,且整体向Y负半轴移动;扇叶的面积会随着压力的增大而减小。
