轨道板张拉力模糊PID同步控制联合仿真分析

张旭飞，刘欣超，李 凯，权 龙

(1.太原理工大学 机械与运载工程学院，山西 太原 030024；2.太原理工大学 新型传感器与智能控制教育部和山西省重点实验室，山西 太原 030024)

引言

CRTSⅢ型无砟轨道板是我国高铁基建领域的新发展成果，已在全国广泛推广应用[1]。预紧力筋张拉是该轨道板生产中的关键工序，直接影响产品成形质量及效率[2]。传统台座法张拉成形过程通过同一张拉活动梁对多根钢筋施加预紧力，需由专人控制并设置大吨位的张拉系统，整个过程工序复杂，效率低，设备投资大，控制精度低，多路钢筋受力不均匀导致的轨道板翘曲变形还会降低成形精度[1,3]。

为此，ZENG Zhiping等[4]基于列车荷载疲劳试验，分析了张拉成形CRTSⅢ轨道板的运动及应变特性；CAI Xiaopei等[5]研究了不同路基冻胀条件下，CRTSⅢ型轨道板不平顺非线性损伤有限元模型；罗昂昂等[6]基于偏差耦合模糊PID同步控制策略，提升了混凝土预制件张拉施工变频泵控液压系统的动态性能及鲁棒性；张长春[2]设计了双向自抗扰同步张拉控制系统，实现了CRTSⅢ型轨道板张拉结构和参数的自动调整及补偿；此外，还有部分学者仿真分析了轨道板其他相关成形工艺，优化设计了相应的液压系统[7-11]。可见，前期针对CRTSⅢ型轨道板张拉工艺的研究仅局限于传统成形设备设计及参数控制系统仿真等方面。

为进一步改善CRTSⅢ型轨道板张拉工艺效率及控制精度，王朝林等[12]设计了各预紧力筋独立设置张拉杆的多通道同步张拉设备，可实现每根预紧力筋张拉力的自动控制。然而，该设备张拉时预紧力筋与张拉杆的螺纹连接滑移，锁紧时插板与张拉杆间的空隙以及液压系统黏性摩擦系数与泄漏系数不一致等问题，均会产生不同程度的张拉力波动及回弹，使各位置预紧力筋内应力分布不均匀，严重影响产品张拉成形质量。

为此，本研究在张拉设备多通道同步液压系统工作原理分析基础上，进行AMESim/Simulink联合仿真，提出基于模糊PID的多通道张拉力波动及回弹控制方法，通过与传统PID控制策略对比仿真分析，验证提出的控制方法对多通道张拉力波动的同步控制性能。

1 张拉设备液压系统运行原理

为研究提出的多通道同步张拉设备控制性能，需首先分析其液压系统结构原理及简化模型。

1.1 张拉设备液压系统结构原理

根据高铁轨道预制标准要求，轨道板内须放置纵向与横向预紧力筋，并采用双向布置的张拉设备在轨道板成形前对预紧力筋进行张拉使，之产生内应力并固定。基于此设计的纵向8组、横向4组多通道张拉设备结构原理如图1所示，预紧力筋一端固定于固定板上，并保证另一端伸出长度相同且具有相同初始预紧力。张拉装置上固定有与模具平行的横梁，每根预紧力筋由一组张拉液压缸进行张拉。每组张拉液压缸由位于预紧力筋两侧对称布置的2个张拉缸组成，各张拉液压缸后端均匀固连于横梁上，前端固定于后导板上。此外，预紧力筋前端与张拉杆均采用螺纹连接，在张拉时，张拉杆固定于后导板。相应的张拉工作原理为：首先，将轨道板成形模具运送至张拉工位；其次，使端向张拉装置与侧向张拉装置进入工作状态；再次，各组张拉液压缸同步运行完成预紧力筋预应力的产生与固定；最后，液压马达驱动锁紧机构对张拉杆进行锁紧(为简化分析，图中省略相应结构)。

1.后导板 2.张拉杆 3.张拉液压缸 4.横梁5.预紧力筋 6.轨道板模具 7.固定板图1 张拉设备液压系统结构原理Fig.1 Structure principle of hydraulic system of stretch-draw equipment

1.2 液压系统数学模型

考虑到各纵向及横向张拉系统具有相同结构，为简化分析，选取其中1个通道为研究对象，相应的集总参数液压伺服张拉力控制原理如图2所示。其中，mt为预紧力筋与后导板等效质量；K和C为预紧力筋等效弹簧刚度及阻尼。

图2 液压伺服张拉力控制原理Fig.2 Principle of hydraulic servo stretch-draw control

力传感器检测张拉力后通过控制装置与指令信号比较，可得控制装置内偏差电压信号为：

Ue=Ur-KfFFg

(1)

式中，Ur为指令电压信号；KfF为力传感器增益；Fg为传感器检测到的液压缸输出力。假设控制装置的传递函数为G2(s)，偏差电压信号经控制装置处理后送入增益为Ka的伺服放大器，产生控制电流ΔI=KaUeG2(s)，驱动伺服阀产生阀芯位移xv，基于阀控液压缸状态方程可得xv至Fg的传递函数为：

(2)

式中，Kce=Kc+Ctp，Ctp为液压缸总泄漏系数，Kc为流量-压力系数；Kq为阀的流量系数；Ap为活塞有效作用面积；ωm为预紧力筋固有频率；ωr为液压弹簧与预紧力筋弹簧串联耦合刚度与阻尼系数之比；ω0及ξ0为液压弹簧与预紧力筋弹簧并联耦合固有频率及阻尼比。

伺服阀控制液压缸产生输出位移，进而对预紧力筋施加张拉力作用，完成整个伺服控制过程，相应的控制系统闭环传递函数为：

(3)

式中，Gsv(s)=xv/ΔI为伺服阀的传递函数，K0=KaApKq/Kce。由于螺纹连接滑移、锁紧结构空隙等因素影响，张拉设备液压系统在进行同步张拉过程中会产生不同程度的张拉力波动及回弹[13]，使各通道预紧力筋内应力分布不均匀，产生各通道张拉力的同步控制误差。为此，基于式(3)可得对应的偏差电压传递函数为：

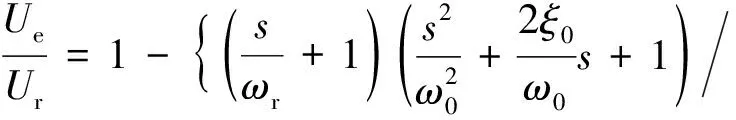
(4)

由式(4)可见，当伺服阀、伺服放大器及力传感器增益选定后，通过合理设置控制装置传递函数G2(s)即可实现液压张拉力偏差的有效控制。

2 多通道张拉力同步控制方法

为保证向多通道预应力筋施加相同内应力，进而提高轨道板成形质量，本节采用PID控制策略实现多路阀控液压缸输出力的同步精确控制。

2.1 模糊PID控制策略

传统PID控制策略以经典控制理论为基础，是工程实际中应用最普遍的控制方法之一。但是，考虑到液压张拉力控制系统在工作时伴随着各种扰动因素影响，PID参数调整困难，采用模糊PID控制策略，根据模糊控制规则表进行模糊推理，实现最优PID控制参数的自动高效调整。图3为模糊PID控制原理，以指令偏差电压Ue及其变化率Uec为输入，经过模糊推理后可得目标输出Kp，Ki，Kd等参数。

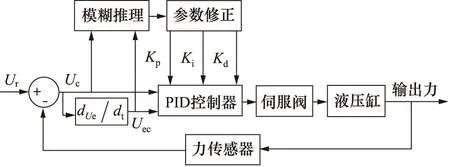
图3 模糊PID控制原理Fig.3 Principle of fuzzy PID control

根据模糊PID控制规律，将Ue，Uec，Kp，Ki，Kd分为7个模糊集：NB(负大)，NM(负中)，NS(负小)，ZO(零)，PS(正小)，PM(正中)及PB(正大)，即模糊子集为{NB，NM，NS，ZO，PS，PM，PB}。根据张拉力同步控制要求，取相应的论域为{-6，-5，-4，-3，-2，-1，0，1，2，3，4，5，6}。假设所有变化参数的隶属度函数均为三角分布，根据PID参数对系统输出特性的影响情况，可总结出系统在被控过程中，对应于不同的偏差Ue和偏差变化率Uec参数时，PID参数的自整定原则，并基于此建立合适的Kp，Ki，Kd参数的模糊规则，如表1～表3所示。

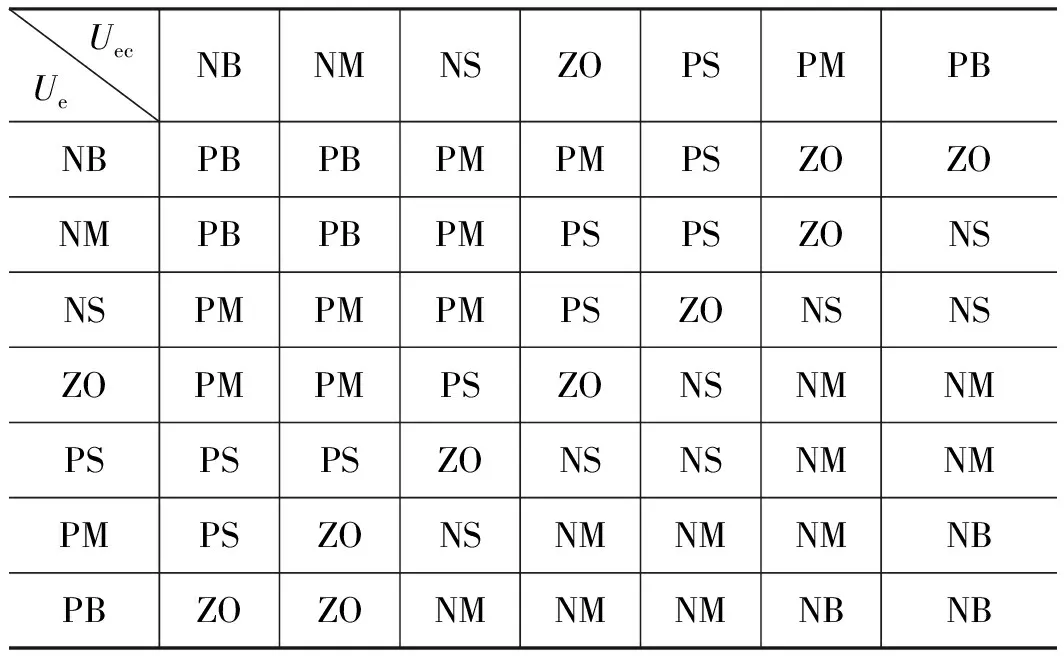
表1 Kp模糊规则Tab.1 Kp fuzzy rule

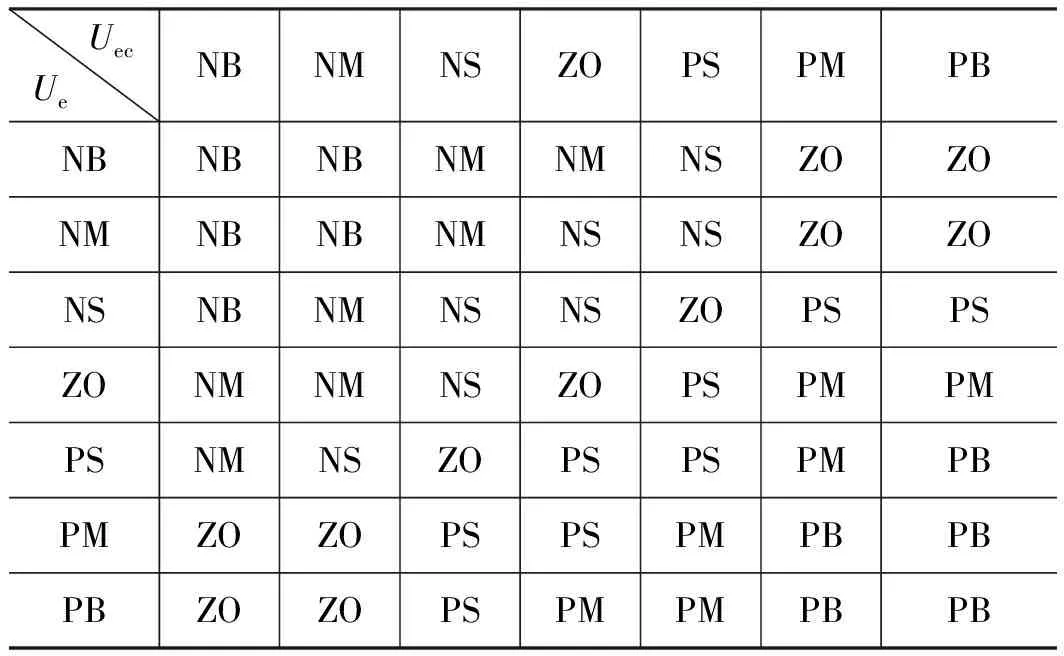
表2 Ki模糊规则Tab.2 Ki fuzzy rule

表3 Kd模糊规则Tab.3 Kd fuzzy rule

为实现自适应模糊PID控制，查表得到修正系数，计算PID参数为：

(5)

式中，系统默认的Kp，Ki，Kd初始取值Kp0=4，Ki0=2

及Kd0=1；|Ue，Uec|p，|Ue，Uec|i及|Ue，Uec|d为在模糊规则表中根据Ue和Uec的取值，将采样数据进行模糊化、模糊推理参数校正、去模糊化等步骤后得到的PID参数变化值与原值相加，即可得到新的Kp，Ki，Kd值，进而实现控制参数自动寻优。

2.2 多通道同步控制

基于上节得到的优化PID参数及离散控制算法，对多通道力传感器反馈信号与指令电压信号比较得到的偏差信号进行调整，减小负载干扰引起的系统误差，即可驱动阀控缸产生准确跟随指令信号的输出力，实现多通道张拉设备输出张拉力的同步精确控制，保证对预紧力筋施加相同的张拉力，满足轨道板产品成形质量的要求。

3 联合仿真分析

为进一步验证提出的多通道张拉力同步控制方法的有效性，本节基于AMESim和Simulink软件分别进行液压系统和传统PID与模糊PID控制系统的联合仿真，对比分析多通道阀控缸在负载干扰力作用下的张拉力同步控制效果。

3.1 液压系统的AMESim仿真模型

建立的张拉设备AMESim液压系统仿真模型如图4所示。电机驱动油泵产生压力油，伺服阀阀芯位移控制液压缸流量，进而控制输出力；在液压缸杆顶部放置位移传感器与力传感器分别采集位移与力信号，送入连接Simulink的联合仿真模块。仿真分析过程设定预紧力筋弹性刚度为1×105N/m，液压缸的无杆腔面积与有杆腔面积分别为4.9×10-4m2和3.77×10-4m2，伺服阀压降为2 MPa，其他参数设置如表4所示。

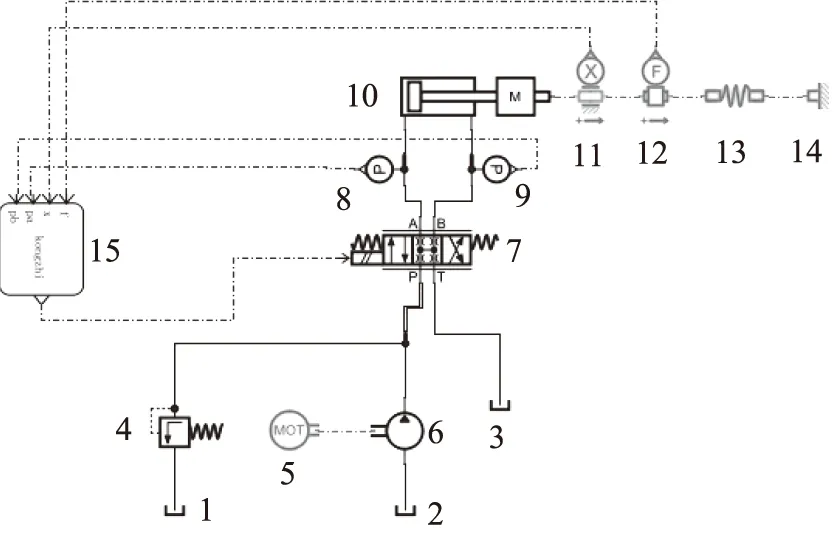
1～3.油箱 4.溢流阀 5.电机 6.油泵 7.电液伺服阀8、9.压力传感器 10.液压缸 11.位移传感器 12.力传感器13.弹簧 14.固定端 15.联合仿真接口图4 AMESim仿真分析模型Fig.4 AMESim simulation analysis model

表4 AMESim仿真参数Tab.4 AMESim simulation parameters

3.2 基于Simulink的联合仿真模型

为实现多通道阀控缸在负载力干扰作用下张拉力同步控制效果的仿真分析，基于图4所示联合仿真接口及表4设定参数，在AMESim仿真模式下调用工具栏中的Simulink模块，即可通过S-函数模块分别实现基于传统PID控制和模糊PID控制算法的预紧力筋张拉力联合仿真分析。

图5为基于传统PID控制算法建立的张拉力液压控制系统Simulink仿真模型，信号源发出指令信号与输出力反馈信号求差，经PID控制器处理后输入用 S-函数模块引入的AMESim仿真模块，控制液压缸产生稳定跟随指令信号的输出张拉力。图6为模糊PID控制液压系统Simulink仿真模型[14]，信号源与指令信号的偏差信号及其微分后的信号同步输入模糊PID控制器，经模糊PID算法计算得到参数最优值后，输入用S-函数模块引入的AMESim仿真模块中，控制液压缸产生稳定跟随指令信号的输出张拉力。

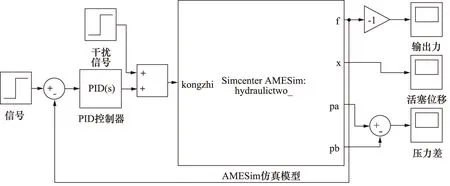
图5 PID控制液压系统Simulink模型Fig.5 PID control hydraulic system Simulink model

3.3 仿真结果分析

基于图4～图6模型，可实现张拉力控制性能的联合仿真分析。首先，设置张拉力控制系统的指令输入为8500 N的阶跃力信号，经图6所示的模糊PID控制模型仿真分析后，得到液压缸两腔压力差Δp如图7所示。可见，在启动后0.5 s内，压力差存在大幅波动，表明液压缸在开始阶段存在死区，0.5 s后压力差逐渐趋于稳定值15 MPa。

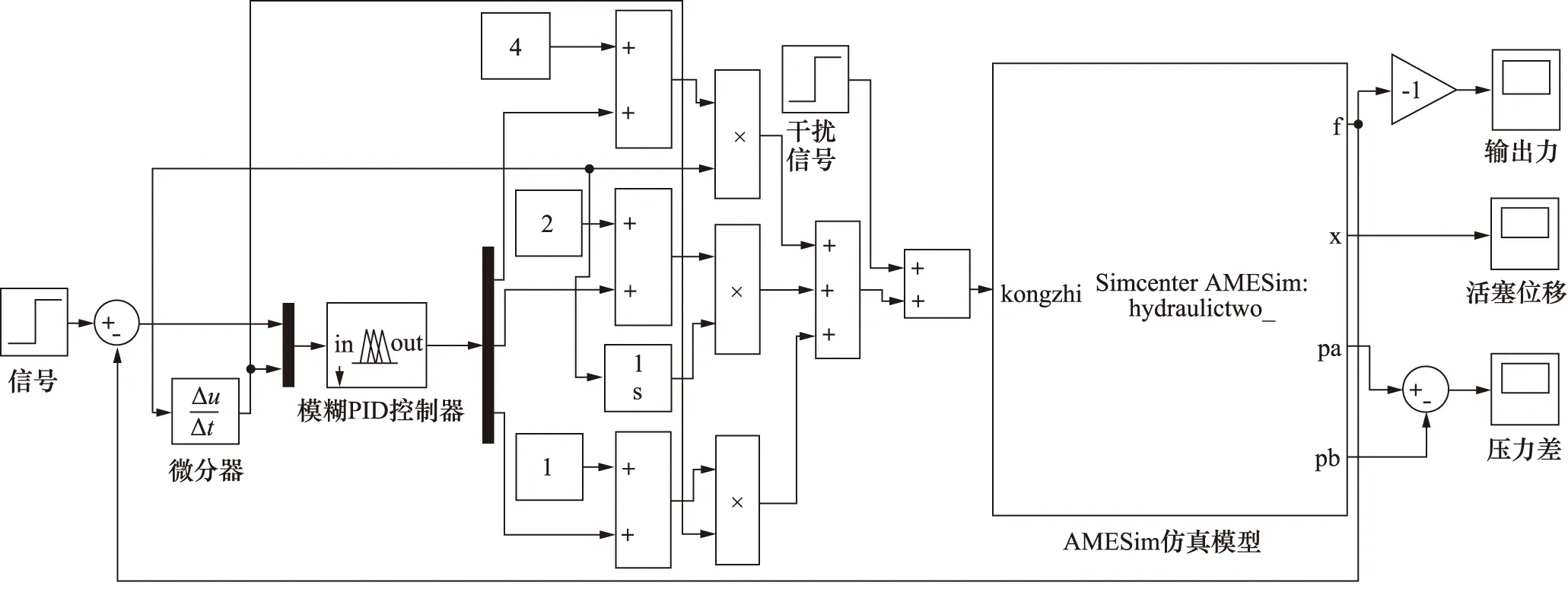
图6 模糊PID控制液压系统Simulink模型Fig.6 Fuzzy PID control hydraulic system Simulink model

图7 液压缸两腔压力差Fig.7 Pressure difference of hydraulic cylinder cavities

为验证提出的控制方法的有效性，在第6秒时，设置液压系统Simulink仿真模型中加入幅值为指令力信号一半的负载干扰输入，经PID及模糊PID算法控制后，得到输出张拉力Fg控制结果如图8所示。可见，两种控制算法均能有效抑制外界干扰对张拉力波动的影响，实现预紧力筋张拉力的精确控制，而且相较于常规PID算法，模糊PID控制超调量更小，响应速度更快，能够使张拉力快速达到稳定状态，具有更好的控制效果。

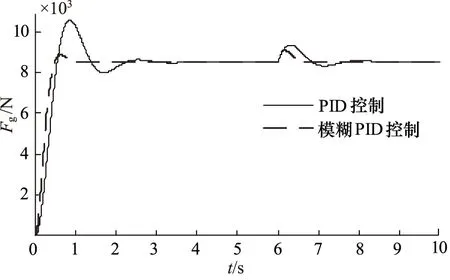
图8 PID与模糊PID张拉力控制结果Fig.8 Control results of PID and fuzzy PID stretch-draw

为进一步分析提出的控制算法对多通道预紧力筋张拉力的同步控制效果，在图1中选取4根预紧力筋与其液压控制系统进行仿真分析。设置各系统的指令输入均为8500 N阶跃力；将液压缸分别编号为1～4，并在第6秒时对其中的液压缸3和4施加幅值为指令力信号一半的负载干扰输入；此外，考虑到液压系统各结构参数存在差异，设置选定的液压缸1～4的泄漏系数分别在0.001～0.004 L/min范围内均匀选取不同值。图9为各液压缸输出张拉力控制结果，可见，对于不同负载干扰力和液压缸泄漏系数，模糊PID控制算法均使各液压缸稳定输出8480 N左右的张拉力，与指令输入的误差未超过1%，表明提出的控制方法可实现多通道张拉力的精确同步控制。

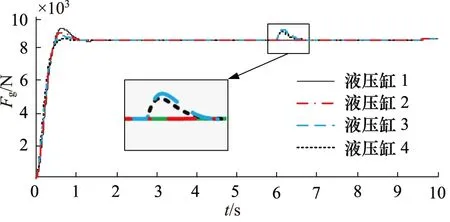
图9 多液压缸张拉力控制结果Fig.9 Stretch-draw control results of multi hydraulic cylinders

4 结论

针对多通道张拉设备张拉力波动影响轨道板成形质量问题，首先结合张拉设备简化结构分析了液压系统运行原理及相应的数学模型；在此基础上建立了张拉液压系统的AMESim仿真模型，并结合Simulink分别实现了基于传统PID和模糊PID算法的张拉力同步控制联合仿真；分析了不同负载干扰力和液压缸泄漏系数作用下，多通道张拉设备的输出特性。结果表明，提出的模糊PID张拉力同步控制算法相较传统PID算法具有更好的响应速度，可将张拉力波动误差控制在1%以内，实现了对多路预紧力筋同步施加一致内应力，可有效提高轨道板产品张拉成形质量。