透视幂函数的常见题型
2021-11-01武兴亮张启兆
■武兴亮 张启兆
幂函数是基本初等函数之一,是在学习了函数的概念与性质之后研究的一种特殊函数。下面举例说明幂函数的常见题型。
一、幂函数的图像
例1图1 中C1,C2,C3为三个幂函数y=xα在第一象限内的图像,则解析式中指数α的值依次可以是()。
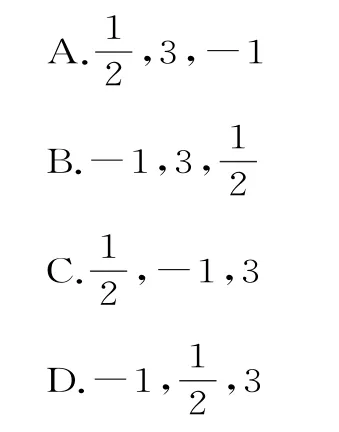
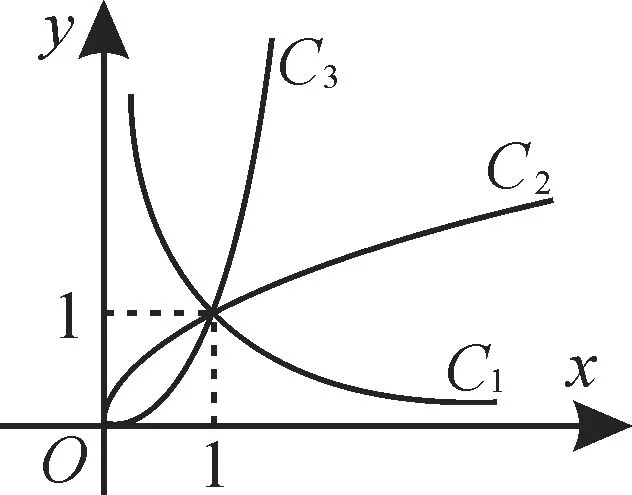
图1
解:由幂函数y=xα在第一象限的图像知,图中C1对应的α<0,C2对应的0<α<1,C3对应的α>1。故指数α的值依次可以是-1,。应选D。
评注:认识幂函数的图像的关键是抓住第一象限的特征。①当α>1时,过点(0,0),(1,1)的抛物线型,且下凸递增;②当α=1时,过点(0,0),(1,1)的射线;③当0<α<1时,过点(0,0),(1,1)的抛物线型,且上凸递增;④当α=0时,即y=1(x≠0),平行于x轴的射线;⑤当α<0时,过点(1,1)的反比例函数,在第一象限内递减,与两个坐标轴的正半轴无限接近。
二、幂函数的性质
例2(多选题)在数学学习与研究中,常用函数的图像来研究函数的性质。下列函数中,在(0,+∞)上单调递增且图像关于y轴对称的是()。
A.f(x)=x3B.f(x)=x2
C.y=x-2D.f(x)=|x|
解:f(x)=x3的定义域为R,在(0,+∞)上单调递增,但f(-x)=-x3≠f(x),即f(x)=x3不是偶函数,其图像不关于y轴对称,A排除。f(x)=x2的定义域为R,在(0,+∞)上单调递增,且f(-x)=(-x)2=x2=f(x),即f(x)=x2是偶函数,图像关于y轴对称,B正确。y=x-2的定义域为(-∞,0)∪(0,+∞),在(0,+∞)上单调递减,C排除。f(x)=|x|的定义域为R,在(0,+∞)上单调递增,且f(-x)=|-x|=|x|=f(x),即f(x)=|x|是偶函数,图像关于y轴对称,D正确。应选B,D。
评注:理解y=x,y=x2,y=x3,y=,y=x-1这五个幂函数的图像与性质是解题的关键。
三、求参数的取值范围
例3已知幂函数f(x)=(m-1)2xm2-4m+2在(0,+∞)上是增函数,函数g(x)=2kx+2。
(1)求m的值。
(2)对任意x1∈[-1,2],总存在x2∈[1,2],使g(x1)=f(x2),求k的取值范围。
解:(1)由题意可得解得m=0。
(2)由(1)知f(x)=x2。记A={y|y=f(x),x∈[1,2]},B={y=g(x),x∈[-1,2]}。容易求得A=[1,4]。由题意得B⊆A,所以即k∈。
评注:第(1)问是利用幂函数的概念及单调性求解的,第(2)问是将问题转化为值域的包含关系求解的。
