函数的概念及其表示重点、难点突破
2021-11-01乔书会
中学生数理化·高一版 2021年10期
■乔书会
函数是高中数学的重要内容,也是高考的常考内容。下面就函数的概念及其表示的重点、难点进行举例分析。
一、重点:函数的三种表示方法
函数有三种表示方法:列表法、图像法和解析法。列表法、图像法和解析法是从三个不同的角度刻画自变量与函数值的对应关系,同一个函数可以用不同的方法表示。应用解析法时,必须注明函数的定义域;应用列表法时,选取的自变量要有代表性,应能反映定义域的特征;应用图像法时,要明确图像是否连线。
例1某商场新进了10台彩电,每台售价3000 元,试求售出台数x与收款数y之间的函数关系,分别用列表法,图像法,解析法表示出来。
解:由题意列表,如表1所示。
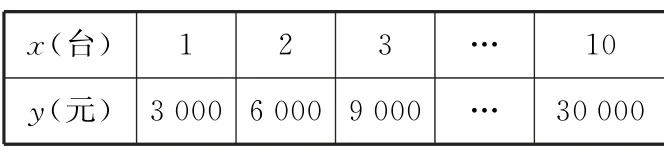
表1
由题意画出图像,如图1所示。
图1
由题意可得函数的解析式为y=3000x,x∈{1,2,3,…,10}。
点评
题中函数的定义域是不连续的,作图时应注意函数图像是一些点,而不是一条直线。求函数的解析式时,应标明函数的定义域。
二、难点:分段函数
分段函数是指在定义域的不同部分,有不同的对应关系的函数。分段函数是一个函数,不要把它误认为是几个函数。分段函数的定义域是各段定义域的并集,值域是各段值域的并集。

(2)若f(a)=3,求实数a的值。
(3)若f(m)>m(m≤-2或m≥2),求实数m的取值范围。
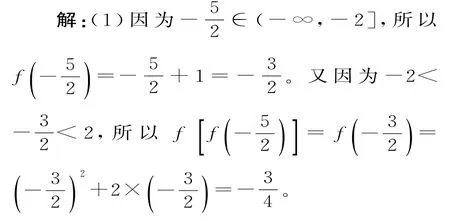
(2)当a≤-2时,由a+1=3,可得a=2>-2,不合题意;当-2 故当f(a)=3时,a=1或a=2。 (3)由f(m)>m,可得或,由此解得m≤-2或m≥2。故实数m的取值范围是(-∞,-2]∪[2,+∞)。
