函数的奇偶性题型直击

■韦 莉

函数的奇偶性是函数的重要性质,也是高考常考的知识点。下面对函数的奇偶性有关的常见题型进行归纳总结,以期对大家的学习有所帮助。

题型1:函数奇偶性的判断

例1已知定义在R 上的函数f(x)和g(x),满足f(0)=1,且对任意的x,y∈R,f(x-y)=f(x)f(y)-g(x)g(y)。试判断函数f(x)的奇偶性。

解:对任意的x,y∈R,f(x-y)=f(x)f(y)-g(x)g(y),令y=x,则f(0)=f(x-x)=f(x)f(x)-g(x)g(x)=f2(x)-g2(x)。

因为f(0)=1,所以f2(0)-g2(0)=1,所以g2(0)=0,即g(0)=0,所以f(-x)=f(0-x)=f(0)f(x)-g(0)g(x)=f(x)。

又因为f(x)的定义域为R,所以函数f(x)为偶函数。

点评

要判断函数f(x)的奇偶性,就需要判断f (x)与f(-x)的关系,故需要对f (x-y)=f(x)f(y)-g(x)g(y)中的x,y进行适当的赋值。赋值法是求解抽象函数问题的常用方法。

题型2:利用函数的奇偶性求函数的值

例2已知函数y=f(x)是定义在R 上的奇函数,当x<0时,f(x)=x2+mx+2,且f(1)=-2,则f(2)的值为____。

成年人平均每天需要8个小时的睡眠，而正处于生长发育期的青少年每天则至少需要9个小时的睡眠。但是由于繁重的课业负担，很多青少年的睡眠时间根本达不到要求，这会严重影响其身心的健康发展。

解:由f(x)是R 上的奇函数,可得f(-1)=-f(1)=2,所以1-m+2=2,解得m=1,所以当x<0 时,f(x)=x2+x+2。所以f(-2)=(-2)2+(-2)+2=4,可得f(2)=-f(-2)=-4。

点评

本题是利用奇偶性求函数的值,解题时,只要抓住自变量与函数值的关系,灵活处理即可。

题型3:利用函数的奇偶性求解析式

例3已知函数f(x)是定义在R 上的奇函数,当x≥0 时,f(x)=x(1+x),则函数f(x)的解析式为_____。

解:设x<0,则-x>0,所以f(-x)=-x(1-x)=-x+x2。因为f(x)是定义在R 上的奇函数,所以f(-x)=-f(x)=-x+x2,可得f(x)=-x2+x=x(1-x)。

故函数f(x)的解析式为f(x)=

点评

解答本题的关键是要求出函数f(x)在各个分区间上的解析式。

题型4:利用函数的奇偶性求参数的值

解:由f(x)在[a2-2,a]上是偶函数,可得解得a=1。因为f(x)是偶函数,所以图像关于x=0 对称,则=0,即b=3。故a+b=4。

点评

函数的定义域关于原点对称是函数具有奇偶性的前提,偶函数的图像关于y轴对称,奇函数的图像关于原点对称。

题型5:利用函数的奇偶性与单调性解不等式

例5已知函数f(x)=-3x3-2x,若f(m-3)+f(-2m)<0,则实数m的取值范围为()。

A.(-∞,3) B.(3,+∞)

C.(-∞,-3) D.(-3,+∞)

解:易知f(x)为R 上的奇函数,且在R上单调递减。由f(m-3)+f(-2m)<0,可得f(m-3)<-f(-2m)=f(2m),所以m-3>2m,解得m<-3。应选C。

点评

利用奇偶性与单调性解不等式时,先利用奇偶性把不等式转化为f[g(x)]>f[h(x)]的形式,再根据单调性把不等式中的函数符号“f”脱掉,即可得到具体的不等式(组)。

题型6:利用奇偶性求解函数的图像

例6函数y=的图像大致为()。

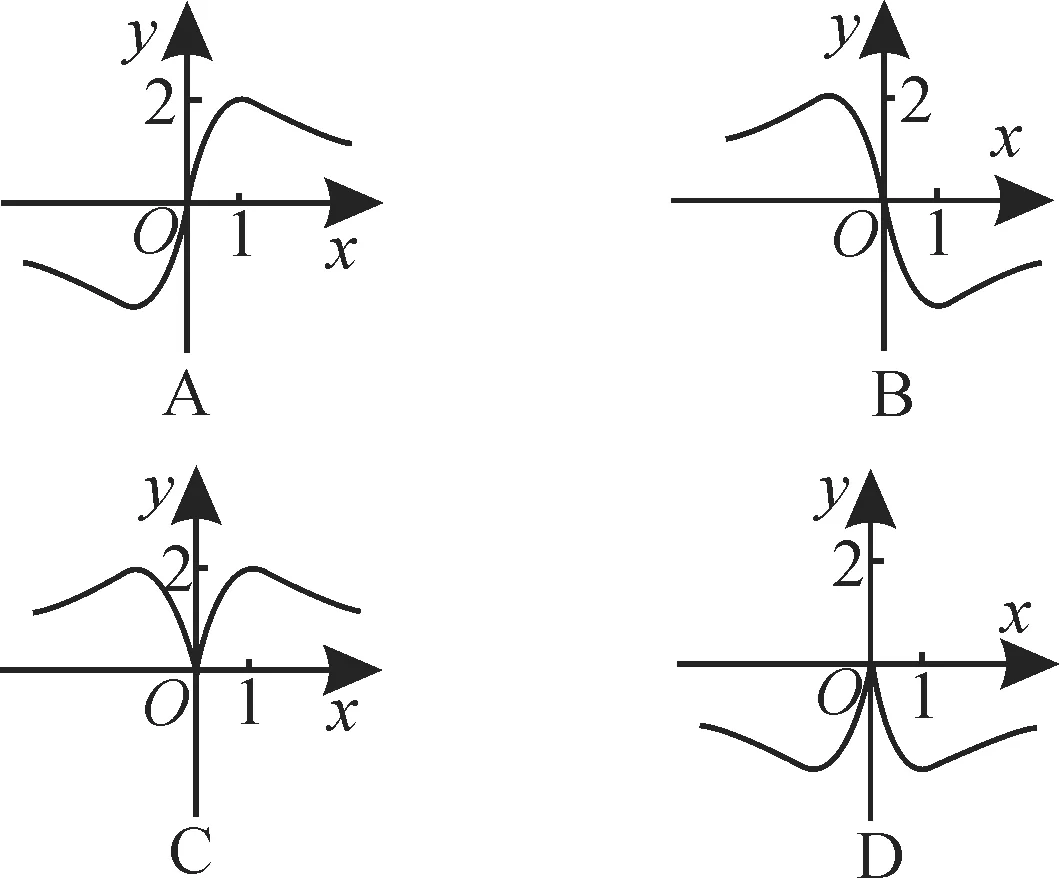
解:易得函数的定义域为R。由函数y=f(-x)==f(x),可知y=f(x)为偶函数,其图像关于y轴对称,所以A,B错误。当x=1 时,y==-2<0,所以C错误。应选D。

点评

判断函数图像可以从以下四个方面入手:根据函数的定义域,判断图像的左右位置;根据函数的值域,判断图像的上下位置;根据函数的单调性,判断图像的变化趋势;根据函数的奇偶性,判断图像的对称性。

感悟与提高

1.若对任意的x,y∈R,都有f(x+y)=f(x)+f(y),则函数g(x)=+f(x)+3 在 [-2021,2021]上的最大值M与最小值m的和M+m=_____。

提示:在f(x+y)=f(x)+f(y)中,令x=y=0得f(0)=2f(0),即f(0)=0。令y=-x得f(x)+f(-x)=f(0)=0,即f(-x)=-f(x),所以f(x)是奇函数。令函数h(x)=+f(x),则h(-x)=+f(-x)=--f(x)=-h(x),可知h(x)是奇函数,所以在对称区间上满足h(x)max+h(x)min=0。当x∈[-2021,2021]时,g(x)max=M=h(x)max+3,g(x)min=m=h(x)min+3,所以M+m=h(x)max+h(x)min+6=6。

2.若函数f(x)=为奇函数,则a=()。

提示:因为f(x)是定义在R 上的偶函数,所以f(2)=f(-2)。因为对任意的x1,x2∈[0,+∞)(x1≠x2),都有>0,所以f(x)在[0,+∞)上是增函数。又1<2<3,所以f(1)