基于微段组合的干气密封端面型槽结构模型及其参数影响
2021-10-31于辰江锦波赵文静李纪云彭旭东王玉明
于辰,江锦波,赵文静,李纪云,彭旭东,王玉明
(浙江工业大学机械工程学院,浙江杭州310014)
引 言
干气密封自20世纪60年代被提出以来,就因其低泄漏、低磨损和长寿命等显著优势而成为中高速旋转机械轴端密封的首选型式[1],并逐渐在低速搅拌器、离心泵上得到应用。密封端面开设的各种流体动静压型槽是干气密封形成具有一定承载和刚度气膜的关键所在,如何通过端面型槽的结构改型优化以实现高气膜刚度和低泄漏是其研究热点之一。John Crane公司最早提出的干气密封专利为密封端面开设对数螺旋槽的结构[2],该结构一直沿用至今。Gabriel在论述干气密封工作原理的经典文献[3]中也指出对数螺旋槽是一种流体动压效应强、气膜稳定性好的干气密封端面结构。不过目前并没有证据证明,在任意压力和速度工况条件下,对数螺旋槽始终是干气密封或气体推力轴承端面结构的最佳选择。
由于自然环境通常难以满足PRB的使用要求,科研人员开始尝试进行人工干预,目前使用最多的是在PRB的外围添加电场,使得地下水中的污染羽在PRB中流速加快,不仅提高PRB的修复效率,同时确保污染的地下水尽可能全部得到修复[13-14].
为改善干气密封在不同工况条件下的密封性能,国内外学者从型线表征函数[4]、型槽结构形状[5]、几何参数优化[6]和三维槽底形状[7-8]等不同角度出发提出了优化策略。很多学者探讨了采用其他经典型线代替对数螺旋线作为端面型槽边界型线的可行性,如斜直线[9-10]、圆弧线[11]和超椭圆曲线[12],并探讨不同型线型槽的适用范围。江锦波等[13]对比了不同经典型线型槽干气密封的稳动态性能,指出在特定工况下,部分经典型线型槽有望获得比对数螺旋槽更大的气膜承载力和刚度。为克服经典型线特征方程表征能力对型槽形状优化的限制,Hashimoto等[14-15]、丁雪兴等[16]、Shen等[17]、魏超等[18]提出了采用样条曲线、多项式曲线等拟合曲线来描述型槽边界,并通过多个几何参数变化来调控曲线形状,从而将形状优化问题转化为多参数优化问题。这为端面型槽型线设计提供了新的思路,并使型线的几何表征能力得到显著提高,不过仍存在着描述型线形状的特征参数几何意义不明确、优化结果难推广等问题。
经典对数螺旋槽边界型线是光滑曲线,也即从型槽入口至出口,型线不会出现周向偏转而形成非连续型线。通过型槽迎风侧或背风侧型线的周向偏转以构造不同的型槽结构,进而改变流体在密封间隙内的流动方向,这也是目前国内外密封公司和学者研究的重要方向。黄莉等[19]、刘坤等[20]对比研究了雁型槽和螺旋槽干气密封的开启和刚度特性,指出雁型槽干气密封具有更佳的动压开启特性;Flowserve公司提出的带内环槽的螺旋槽则是将雁型槽下游侧的环槽进一步周向延伸形成贯通结构,其相较于经典螺旋槽在低速或静压条件下具有更大的气膜承载力和刚度[21-22]。呼延晨龙等[23]和陶丹萍[24]提出一种双叶翼型组合槽结构,其通过将经典螺旋槽迎风侧或背风侧侧壁进行一定角度的周向偏转而形成收敛状结构。上述的型槽结构改型带有一定的随机性,且不同结构型槽的参数定义体系各不相同,这不利于干气密封性能的充分优化。
综上所述,现有端面型槽边界型线描述方程几何表征能力不强、参数几何意义不明确,以及不同结构型槽的参数定义体系不统一的问题在一定程度上限制了端面型槽结构的充分优化,而提出一种几何表征能力更强的端面型槽边界型线表征模型,并使其能覆盖描述不同几何型线和周向偏转结构的端面型槽则有望解决该问题。
pa——环境压力,MPa
本文基于型线径向等分微段并组合的思想,提出了一种型槽边界型线几何表征能力更强的广义对数螺旋槽结构模型,给出了广义螺旋槽的参数定义体系及该模型对不同结构形状型槽的表征示例,对比研究了不同压力和速度下广义螺旋槽和经典螺旋槽干气密封的稳态性能,重点探讨了广义螺旋角分布和周向偏转角等两个特征量对广义螺旋槽干气密封性能的影响,基于不同目标函数获得了广义螺旋槽的最优结构形状,为气体密封与轴承端面型槽设计提供了新的思路。
1 分析模型
1.1 型线表征函数推导
干气密封端面型槽轮廓由上游入口边界、下游出口边界和两侧壁边界形状共同决定。图1所示为一类典型的端面型槽结构,其特点是型槽入口边界和出口边界都为连续圆弧线,侧壁边界型线可为对数螺旋线、圆弧线或直线等不同型线,且可为周向无错位的光滑连续型线或周向有错位的非连续型线。因不同型线的表征方程各不相同,且不同结构型槽的参数定义也不相同,这种因型槽型线方程和参数体系不同而造成的不同型槽之间的离散分布现象在一定程度上限制了干气密封端面型槽的结构优化水平及密封性能发挥。提出一类新的端面型槽侧壁边界型线表征函数,使其可统一表征包括图1所示所有结构在内的型槽结构,有望解决因型线表征方程和参数定义体系不统一所带来结构优化不充分的难题。
专利信息传播利用的体系化建构与创新............................................................................................王 肃 11.75
广义螺旋角β(r)的径向分布规律决定了侧壁型线形状,其可以是沿直线、圆弧线或椭圆线等不同规律分布。引入几何表征能力很强的超椭圆曲线分布以表征广义螺旋角沿径向分布规律,使其表征结果更具有一般性。图3所示为基于超椭圆曲线的广义螺旋角径向分布,其表达式为:
经典对数螺旋线的极坐标表达式为:
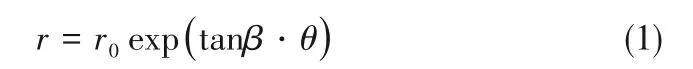
式中,r0为起始半径;r和θ分别为极径和极角;β为螺旋角。定义任一型线在半径r处圆周切线与型线切线之间的夹角为广义螺旋角β(r),其沿径向呈一定规律分布,其中对数螺旋线属于广义螺旋角沿径向恒为定值的特例。
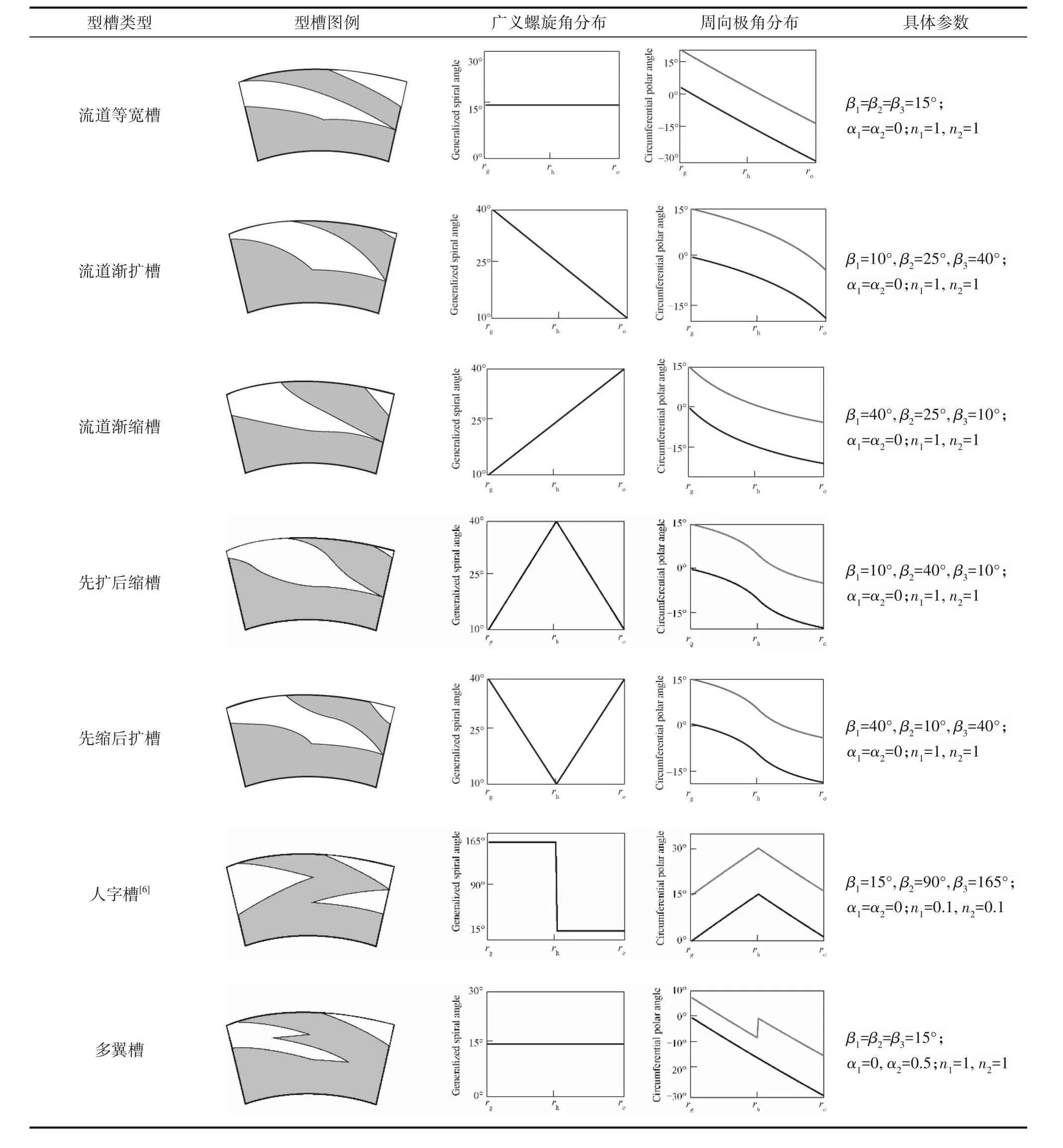
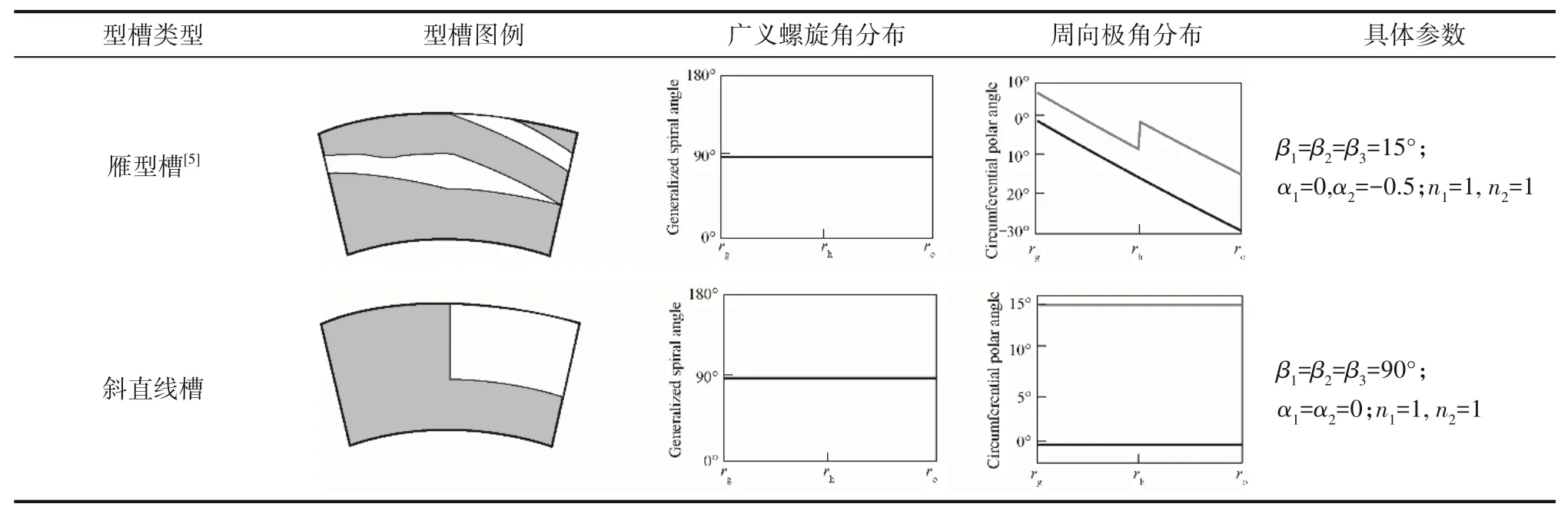
图2所示为一种典型的广义螺旋槽端面干气密封结构及其参数定义示意图。在靠近密封端面外径ro至槽根半径rg处开设有数量为Ng、深度为hg的周向均布广义螺旋槽,在密封端面内径ri至槽根半径rg之间设有不开槽的密封坝,密封坝处的气膜厚度为h0。为方便起见,规定一个型槽中顺着转动方向的两侧壁依次被称为迎风侧和背风侧侧壁,如图2(d)所示。考虑到有些端面型槽的侧壁型线会出现周向错位的非连续特征(如图1(g)所示的雁型槽),设背风侧和迎风侧侧壁型线在转折半径rh处有周向偏转角θ1和θ2,位于rh和ro之间且靠近高压侧的型槽称为上游槽,位于rh和rg之间且靠近低压侧的型槽称为下游槽,规定从下游槽至上游槽逆着转速方向偏转时周向偏转角为正,反之为负。侧壁型线在入口半径ro、转折半径rh和出口半径rg(也即槽根半径)处的广义螺旋角分别为β1、β2和β3。显而易见的是,型槽周向最宽处始终位于转折半径rh处,该半径处一个周期内的周向开槽角度和对应密封堰角度分别为θh和θ0。定义周向槽宽比δ为转折半径rh处开槽区周向夹角θh与一个周期周向夹角(θh+θ0)之比,分别定义迎风侧偏角系数α2、背风侧偏角系数α1为迎风侧周向偏转角θ2、背风侧周向偏转角θ1与开槽区周向夹角θh之比。定义径向槽长比γ1和上游槽长比γ2以分别表征端面型槽整体和上游槽的开槽比例:
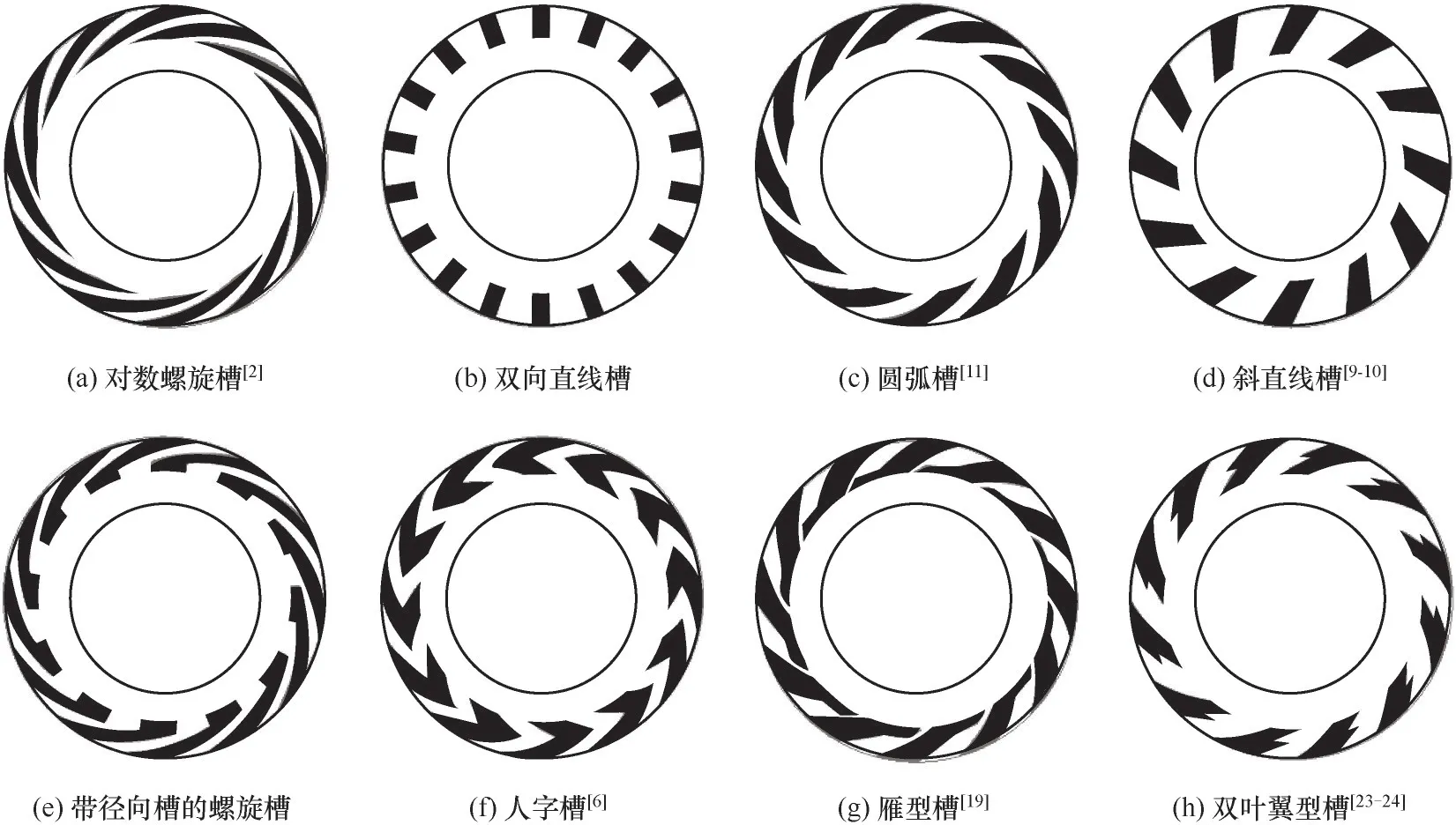
图1 一类典型的干气密封端面型槽结构示意图Fig.1 Schematic diagram of some typical dry gas seal surface groove structure
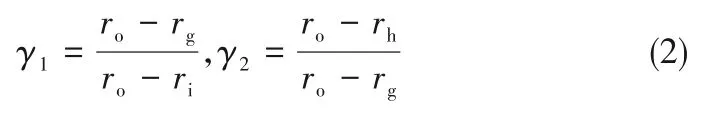

图2 广义对数螺旋槽干气密封及型线参数定义图Fig.2 Generalized logarithmic spiral groove dry gas seal and profile parameter definition diagram
对于单向广义螺旋槽,当迎风侧和背风侧型线发生非连续周向偏转时,呈现的型槽结构和槽根周向夹角θg表达式如表1所示。根据给定的槽数Ng和周向槽宽比δ可计算出rh处的周向角度θh,进而根据表1所示的公式计算出槽根半径rg处的周向夹角θg。进一步,可用式(3)统一表征迎风侧和背风侧不同偏转角时的槽根周向夹角θg:

表1 单向广义螺旋槽型线非连续偏转及开槽角度Table 1 Discontinuous deflection and slotting angle of unidirectional generalized spiral groove

密封端面型槽侧壁型线形状由广义螺旋角β(r)分布和转折半径处的周向偏转两者共同决定。将型线沿径向等分为m段,每个微段型线用对数螺旋线表征,第j段对数螺旋线对应的半径rj为:
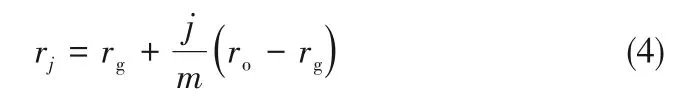
实际上,将端面型槽沿径向等分成若干段,当径向分段数足够多时,每一微段边界型线都近似可看成是直线、圆弧线或对数螺旋线。鉴于对数螺旋线在干气密封端面型槽设计中的应用广泛性和其表征函数的使用便捷性,不妨将任意边界型线看成是由无限多段螺旋角沿径向呈一定规律分布的对数螺旋线径向首尾相接而成,可称为广义对数螺旋线,由广义对数螺旋线作为侧壁边界型线的端面型槽可称为广义螺旋槽。

图3 基于超椭圆曲线的广义螺旋角径向分布Fig.3 Radial distribution of generalized spiral angle based on hyperelliptic curve

式中,n为超椭圆系数,当n=1和2时,广义螺旋角沿径向分别呈直线和椭圆线分布;a和b分别为径向半径范围和广义螺旋角变化范围;Δr和Δβ(r)分别为半径差值和广义螺旋角差值。
上游槽和下游槽的侧壁型线广义螺旋角分布可相同也可不同,其对应的超椭圆系数分别为n1和n2,则其任意半径rj处的上游槽广义螺旋角β1j和下游槽广义螺旋角β2j满足如下关系:
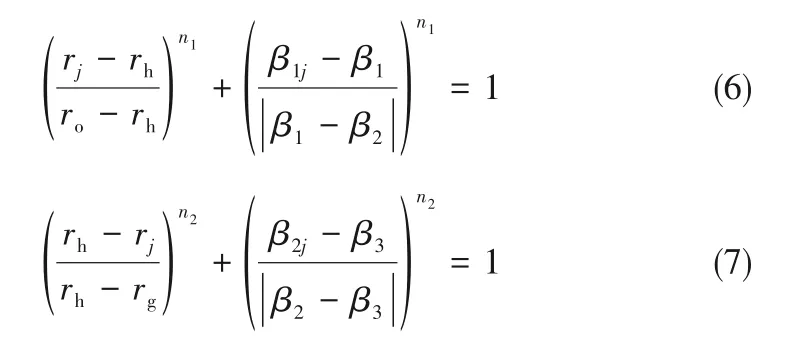
进一步,广义螺旋角β1j和β2j可分别表示为:


不同半径rj处的广义螺旋角βj可统一表示为:
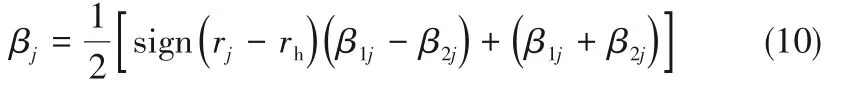
根据式(1),对于任意由对数螺旋线表示的型线微段,其对应的周向夹角为:
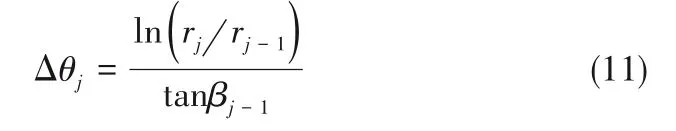
因广义对数螺旋线是由若干微段对数螺旋线首尾相接形成,则广义螺旋线的极坐标方程可表示为:
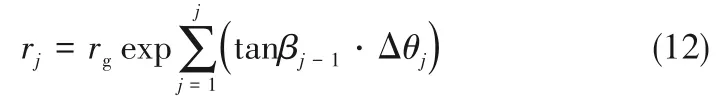
考虑到型线在转折半径rh处发生周向非连续偏转的可能性,则背风侧和迎风侧型线在任意半径rj处的极角θ1,j和θ2,j可分别表示为:
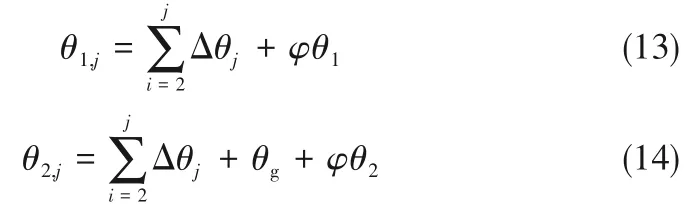
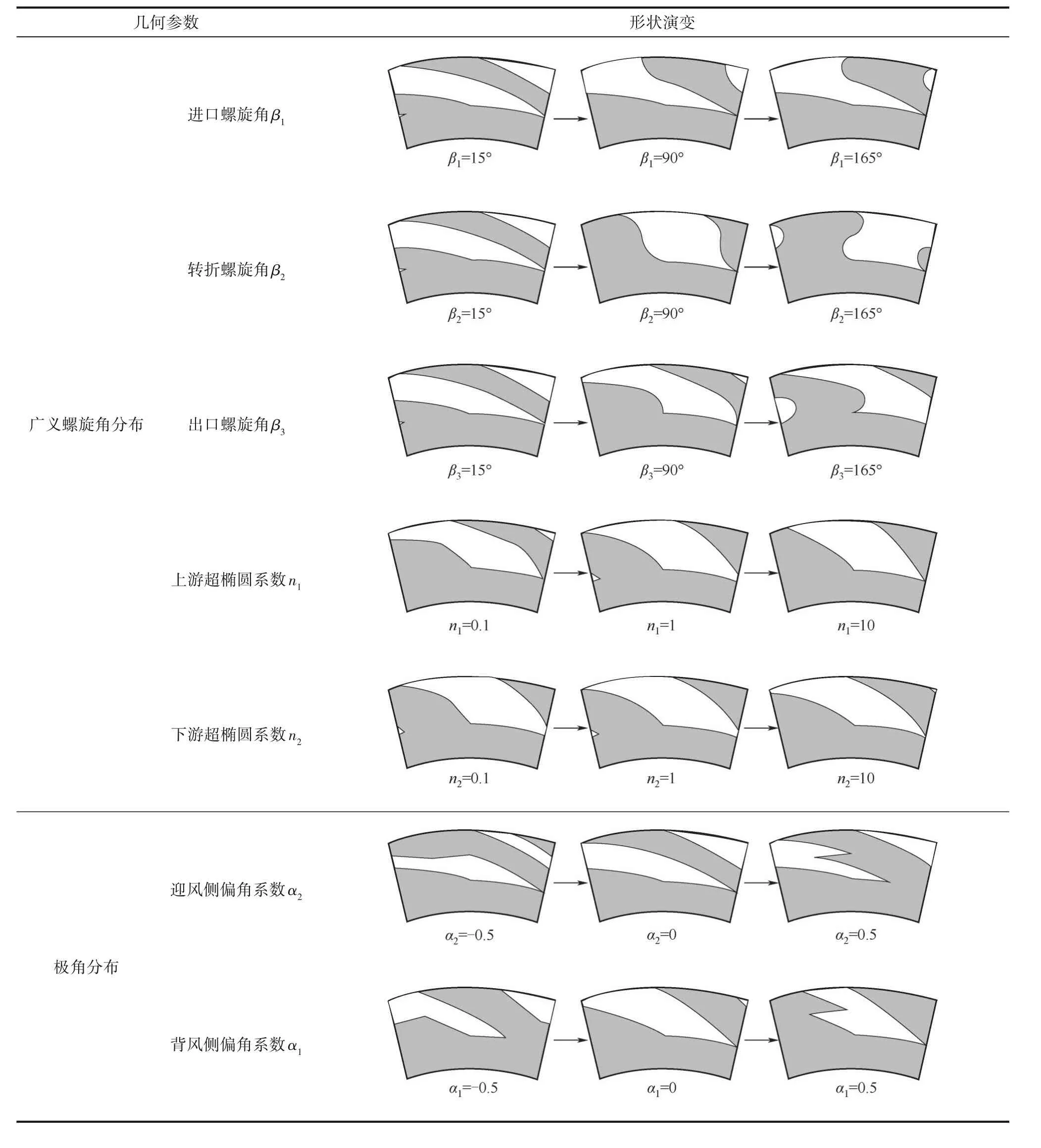
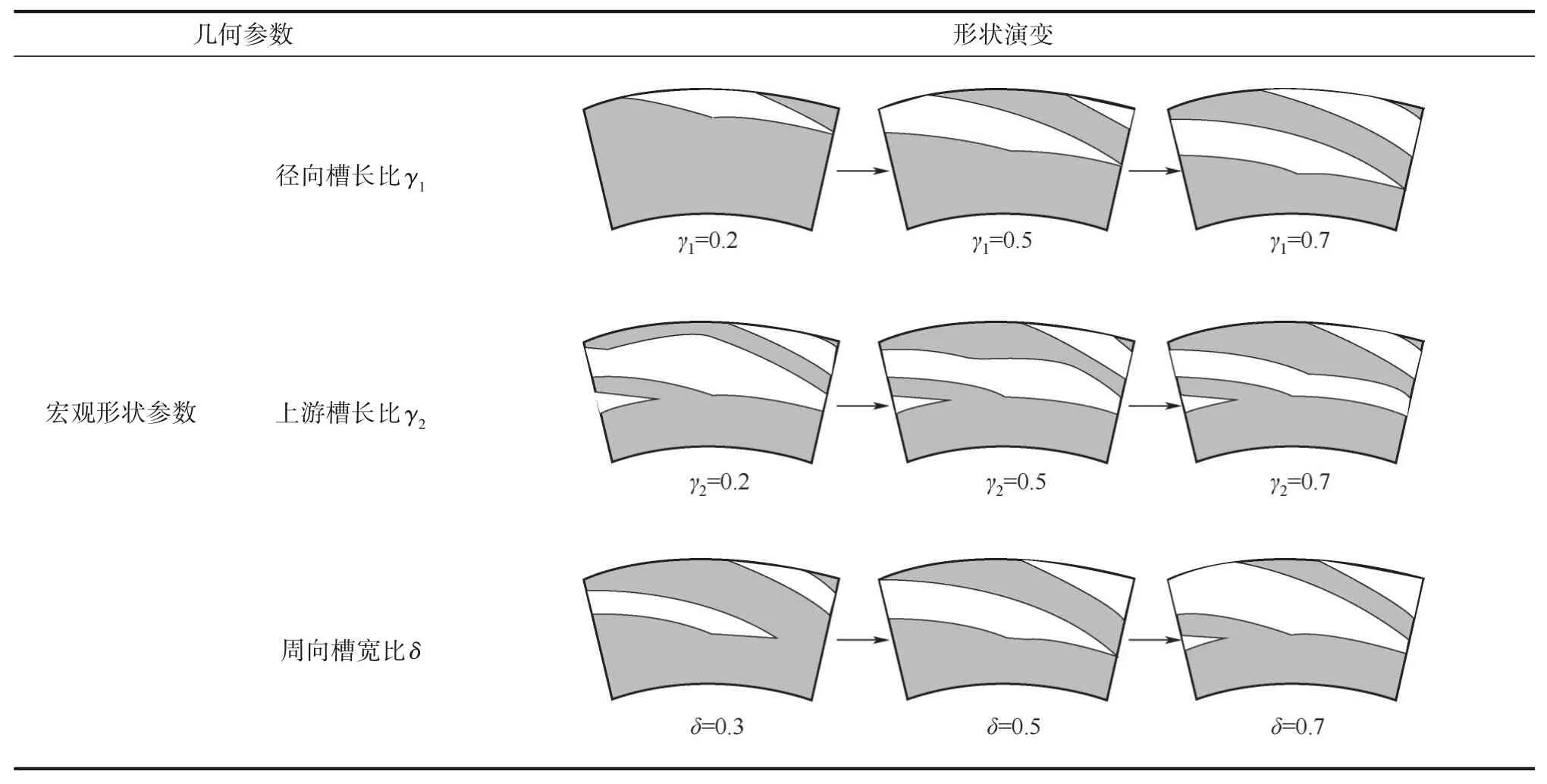
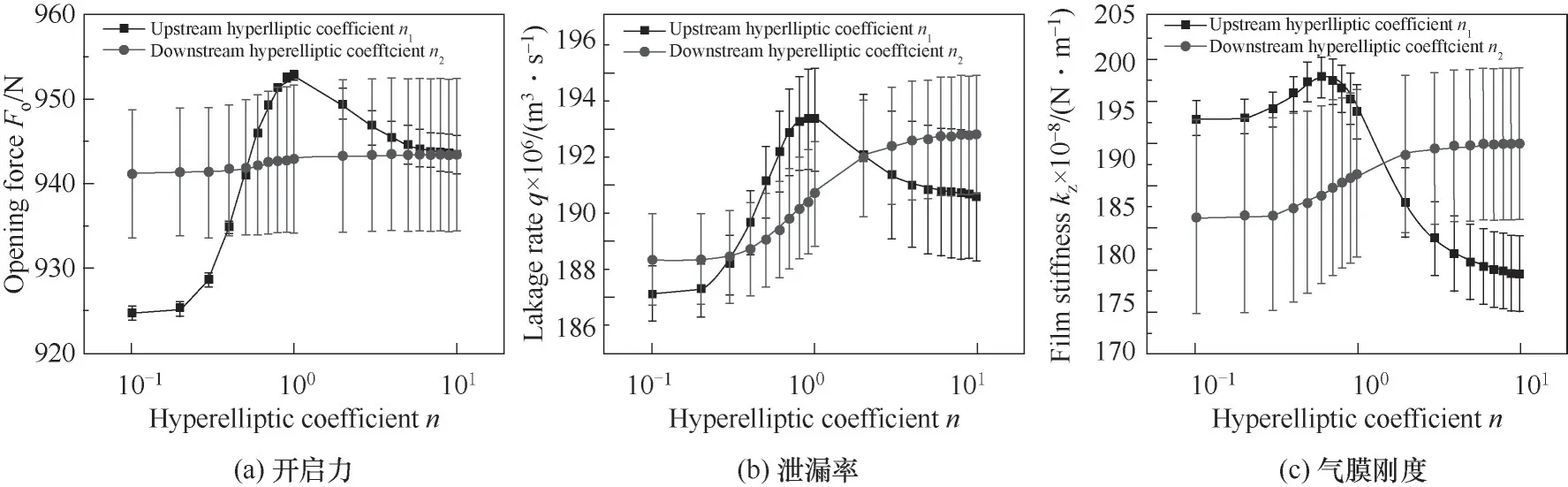
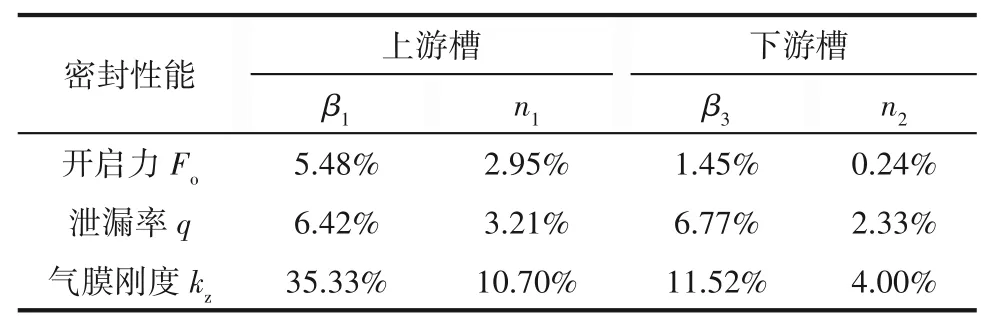
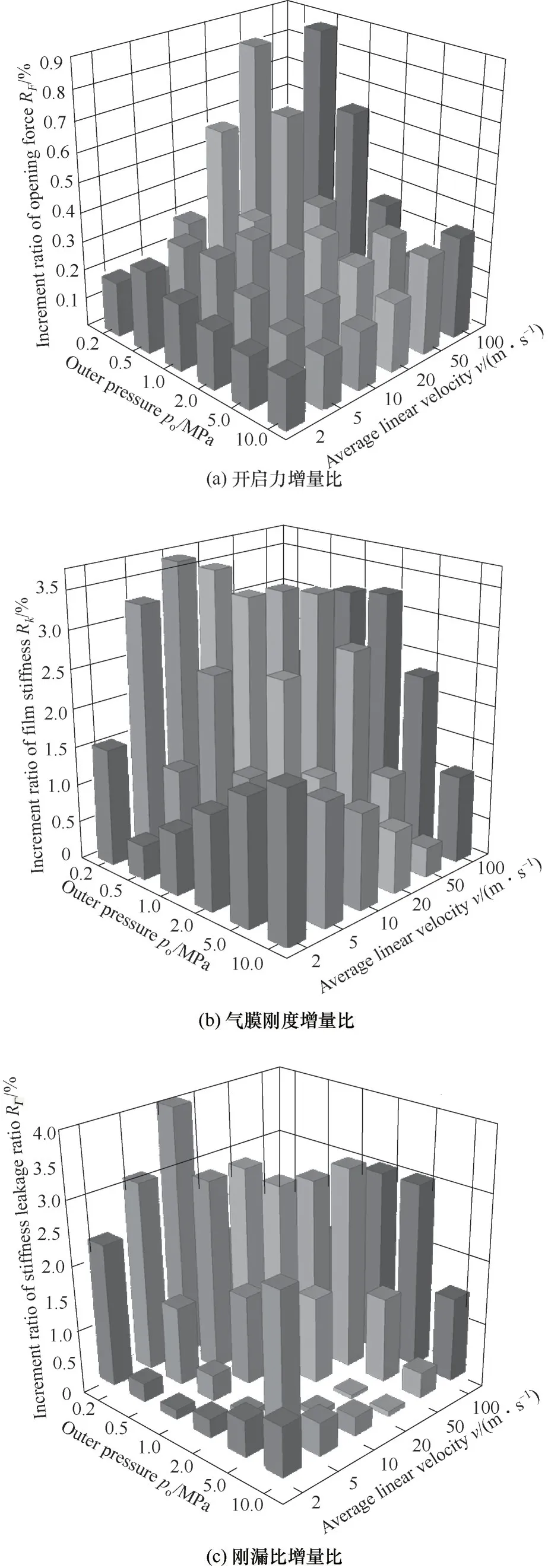
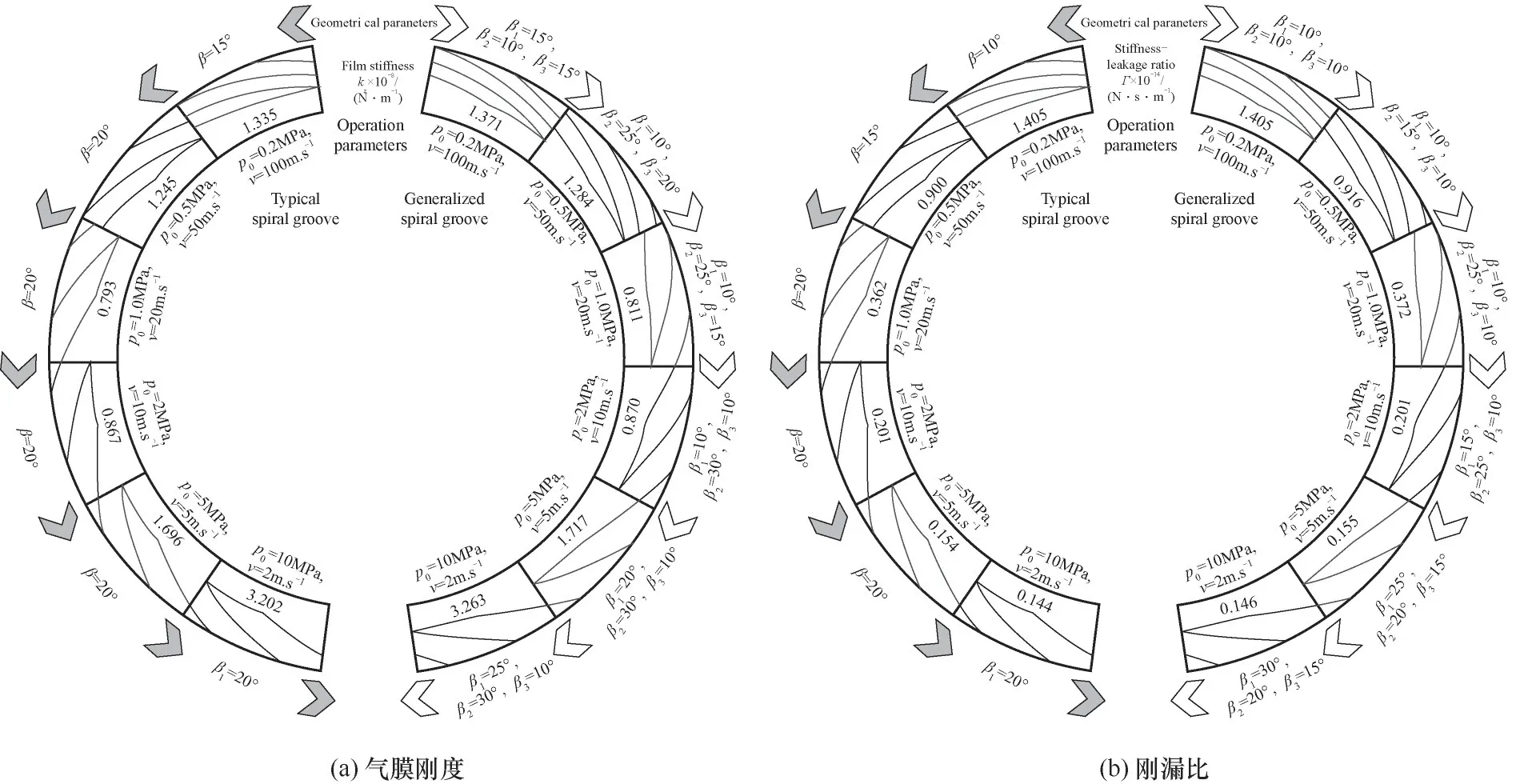
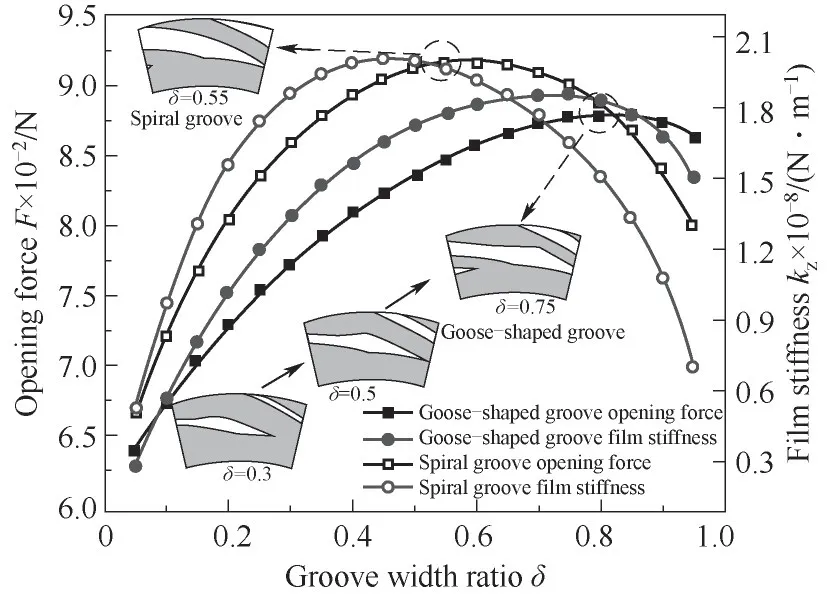
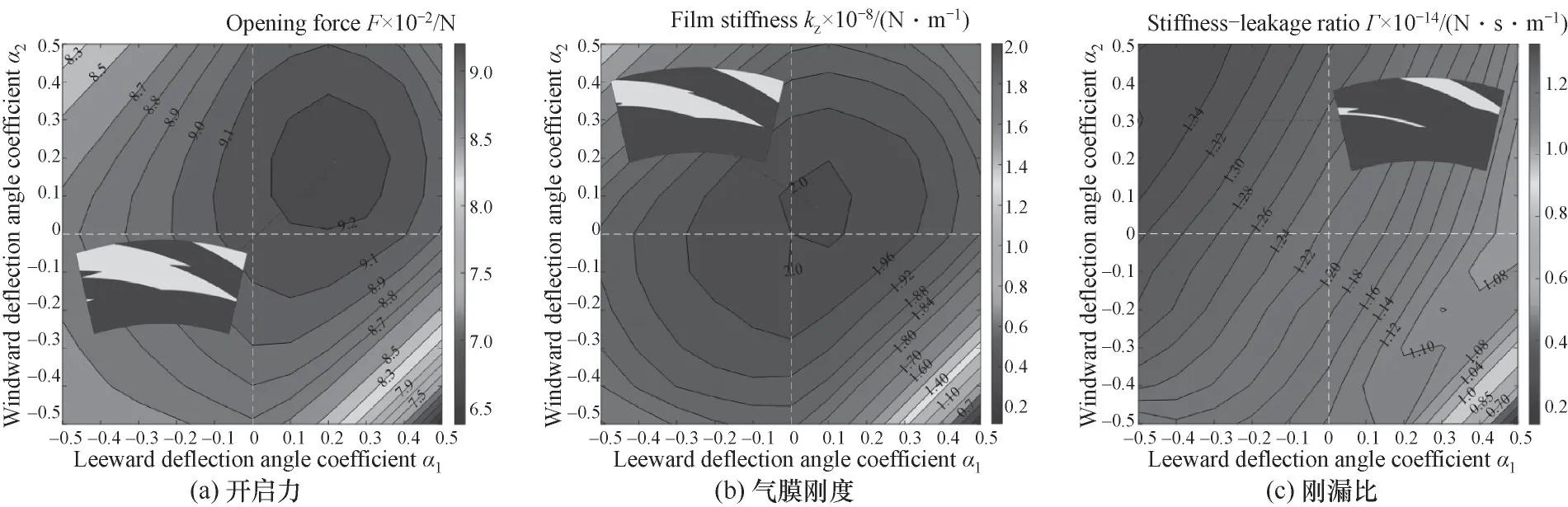
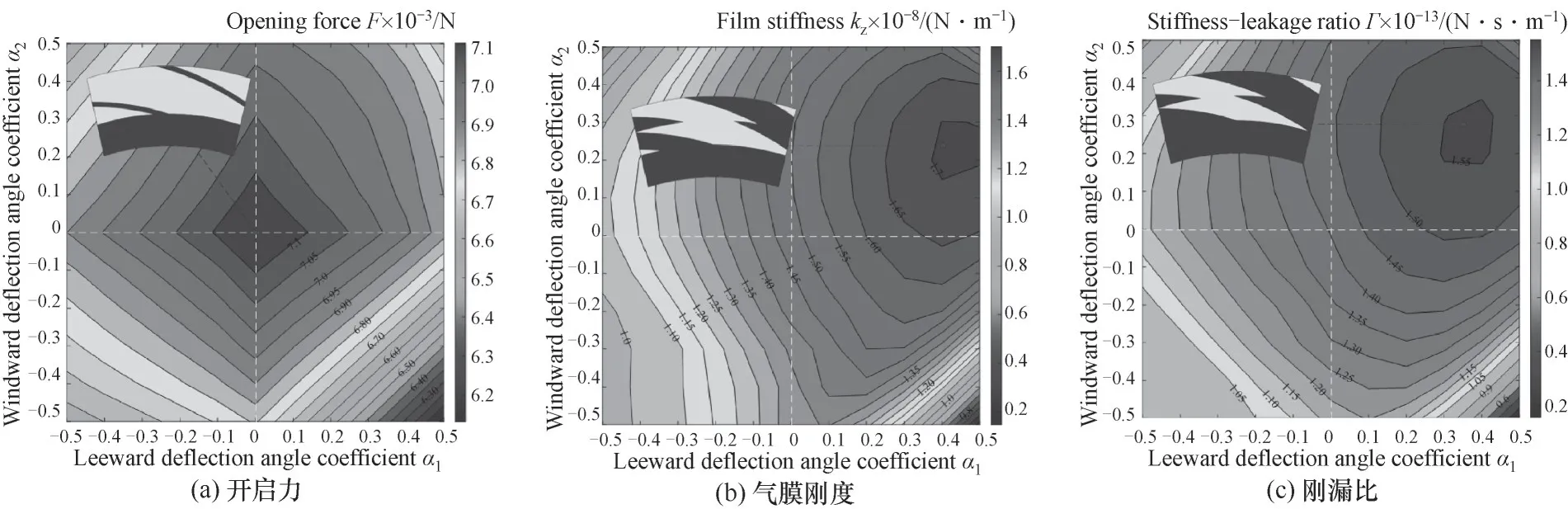
式中,φ为逻辑判断准数,当rj≤rh时,φ=0;当rh 在已知型线上任意半径rj处的周向角度θj基础上,获得背风侧和迎风侧的广义螺旋线直角坐标方程为: 在此基础上,结合槽根半径rg处的型槽出口圆弧线和外径ro处的型槽入口圆弧线边界,则可确定出广义对数螺旋槽的形状。 对于经典对数螺旋槽,其几何轮廓由周向槽宽比δ、径向槽长比γ和螺旋角β这三个几何参数即可描述;而对于广义对数螺旋槽,除了描述其宏观形状的3个几何参数(周向槽宽比δ、径向槽长比γ1和上游槽长比γ2)之外,还有5个表征其广义螺旋角分布规律的参数:进口螺旋角β1、转折螺旋角β2、出口螺旋角β3、上游槽超椭圆系数n1和下游槽超椭圆系数n2,以及2个表征其极角分布的参数:背风侧偏转角系数α1和迎风侧偏转角系数α2。 表2所示为不同几何参数对广义螺旋槽形状的影响。从表中可看出,广义螺旋槽中各几何参数具有很强的几何意义:周向槽宽比δ和径向槽长比γ1决定了型槽周向和径向的开槽比例;上游槽长比γ2决定了上游槽在整槽中的径向开槽比例;进口螺旋角β1、出口螺旋角β3和转折螺旋角β2分别决定了型槽入口、出口和两者之间某转折点处的侧壁角度,对其型槽形状影响显著;上游槽超椭圆系数n1和下游槽超椭圆系数n2则分别影响上游槽和下游槽型线角度变化规律;迎风侧偏转角系数α2和背风侧偏转角系数α1则影响型槽迎风侧和背风侧的周向偏转角度,进而影响型槽的整体结构。 表2 广义螺旋槽结构参数取值对型槽形状的影响Table 2 The influence of generalized spiral groove structure parameters on the shape of groove 相较于常规的型槽结构表征模型,广义螺旋槽模型的优势在于可通过采用一些具有实际几何意义的特征参数描述型槽结构,再结合一些多参数优化算法,可实现将型槽结构优化问题转变为更易求解的多参数优化问题。表3所示为不同几何特征参数取值对应的广义螺旋槽结构形状、广义螺旋角分布和周向极角分布。从表中可看出,基于广义螺旋槽结构模型和参数定义体系,通过几何特征参数的不同取值,可实现广义螺旋槽向不同形状和结构型槽的演变。如仅通过改变β1、β2和β3,可实现广义螺旋槽向流道等宽槽(如经典对数螺旋槽[2]和双向直线槽)、流道渐扩槽(如圆弧槽[11])、流道渐缩槽(如斜直线槽[9-10])、先扩后缩槽和先缩后扩槽的转变;当入口螺旋角为锐角、出口螺旋角为钝角,且超椭圆系数较小时,型槽演变为带反向泵送槽的人字槽[6];当迎风侧或背风侧型线的偏转角系数不为零时,型槽演变为雁型槽[19]、多翼槽[23-24]等结构。 续表2 表3 不同特征参数取值对应的广义螺旋槽形状Table 3 Corresponding characteristic parameters of generalized spiral groove shape 干气密封端面间的密封流体可以假设为层流、等温的等黏度气体,则计算密封端面气膜压力的无量纲稳态雷诺方程为: 式中,无量纲参数分别定义为: 式中,p和h分别为密封端面任意点的气膜压力和气膜厚度;pi为内径处压力;Λ为密封压缩数;μ为气体黏度;ω为角速度。 rj——第j段对数螺旋线对应半径,mm 经过个性化调整,医院把分时段预约进一步精细化,预约时间具体到分钟。同时,医院还为患者提供动态等候讯息,推出“排队等候提醒”服务,患者通过手机即可查询排队情况,等候更加灵活,不再局限于候诊区。 周期性压力边界条件为: 全局Moran's I取值范围为[-1,1],I>0表明各样本点互为正相关,且值越大,正相关程度越大;I<0表明各样本点互为负相关;I=0表明没有相关性。 图4所示为干气密封气膜压力和稳态性能求解流程图。首先给定工况条件、几何参数和压力边界条件,基于有限差分法划分计算域网格,其中周向网格数和径向网格数分别为280和150;采用超松弛迭代法求解雷诺方程以获得密封端面压力分布,以密封端面膜压之和的相对误差作为收敛判据,收敛残差为10-5,当达到收敛精度后输出气膜压力分布,进而求解开启力、气膜刚度、泄漏率和刚漏比等稳态性能参数。 对学生的德育教育,应该在具体的情境中去强化训练,让学生在丰富的活动中接受教育。因此学校要定期设计、组织丰富多彩的德育活动,把对小学生的习惯培养融入到教育教学的每一个环节。如,可以以信念、责任、合作、感恩、诚信等专题教育为内容,定期开展主题班会、征文比赛、专题演讲等系列活动,开展小学生课堂行为习惯达标、养成教育签名以及“好习惯伴我行”等系列活动,组织每月一次的学生才艺展示,每学期一次的田径运动会,每学年一次的感恩教育等活动,举行课间舞、拔河比赛、校园十佳歌手评选等活动。这样把养成教育贯穿于教育教学工作的全过程,渗透到学生学习、生活的每个环节,真正做到“真实情景中的德育教育”。 图4 干气密封气膜压力和稳态密封性能求解流程图Fig.4 Flow chart for solving gas film pressure and steady-state sealing performance of dry gas seal 基于本文所提出的广义对数螺旋槽干气密封,研究了不同压力和速度条件下广义螺旋角分布和周向偏转结构对干气密封稳态性能参数的影响,探讨了不同工况下广义螺旋槽的最佳形状及关键几何参数的优选值范围。在研究某一个或多个结构参数的影响规律时,其他结构参数固定不变。除特别说明外,下文计算所基于的干气密封运行工况参数和结构参数缺省值如表4所示。 续表3 表4 干气密封运行工况及结构参数缺省值Table 4 Operating conditions and structural parameter default values of dry gas seal 对于由若干段首尾相接的对数螺旋线所组成的广义螺旋线,其径向分数段对最终成型的型线形状影响显著,只有当分段数足够多时,所形成的广义螺旋线才接近光滑曲线。研究了径向分数段对广义螺旋槽干气密封稳态性能的影响,以确定后续研究中径向分数段的选取值。图5所示为径向分段数对广义螺旋槽干气密封开启力和泄漏率的影响,其中所选取的广义螺旋槽包括广义螺旋角为β1=15°、β2=30°、β3=45°的流道渐扩槽和β1=15°、β2=90°、β3=165°的反向泵送槽。随着径向分段数的增加,两种广义螺旋槽的侧壁型线都逐渐趋于平滑,开启力和泄漏率都呈现减速递增的变化趋势,也即当径向分段数超过一定值时,其开启力和泄漏率基本不再变化。对于流道渐扩槽干气密封,当径向分段数超过18和55时,其开启力和泄漏率的相对误差都控制在0.1%以内;而对于反向泵送槽干气密封,当径向分段数分别超过75和85时,其开启力和泄漏率相对误差控制在0.1%以内。为使广义螺旋线尽量平滑,后续研究时径向分段数都取为100。 3.注重生态环境保护建设,促进绿色低碳循环发展。产城融合的基本原则之一是集约高效、生态环保、绿色低碳。新疆位于西北内陆,生态环境保护和低碳绿色发展极为重要,不能因噎废食,只顾产城融合发展。因此,一方面要合理利用土地,对城镇开发边界要合理控制,实行严格的耕地保护制度和节约用地制度,切实保护好基本农田,不要逾越耕地红线。新疆经济社会的各项建设必须符合土地利用总体规划,提高土地使用效率。另一方面,要大力倡导绿色低碳和循环产业的发展,加大科技研发投入的力度,培育和创新符合新疆自身特色的节能环保绿色产业,重构产业生态安全格局。 图5 径向分段数对广义螺旋槽干气密封性能的影响Fig.5 The influence of the number of radial segments on the performance of generalized spiral groove seal 广义螺旋槽与经典螺旋槽的本质区别在于广义螺旋角分布,前者沿径向可为任意函数分布,而后者沿径向恒为定值。根据表2可知,广义螺旋角分布由三个螺旋角β1、β2、β3和上下游槽超椭圆系数n1、n2共同决定,其中上游槽侧壁型线形状主要取决于β1、β2和n1,下游槽侧壁型线形状取决于β2、β3和n2。通过研究三个螺旋角及超椭圆系数对干气密封稳态性能参数的影响,探讨给定工况条件下型槽侧壁最佳型线形状及其关键影响因素。 (PS: The term dispositions refers to belief, attitude and value in NCATE Glossary.) 如图1所示,理论上四旋翼飞行器实现垂直运动是通过控制四个电机同时增加输出功率,使四个旋翼的转速都增加来增大总升力,当总升力足以克服飞行器总重力时,四旋翼飞行器便会离开地面做垂直上升动作;反之,同时减少四个电机的输出功率,当总升力不足以克服飞行器总重力时,四旋翼飞行器便会做垂直下降动作;当外界扰动量[17]为零,且旋翼所产生升力等于飞行器总重力时,飞行器便保持悬停状态。 鉴于锐角螺旋角的螺旋槽干气密封较钝角螺旋角的反向泵送槽干气密封能获得更大的气膜承载力和气膜刚度已成为共识,下文研究时选取的三个螺旋角取值都为10°~90°范围内的锐角。图6所示为不同螺旋角参数组合条件下对应的广义螺旋槽干气密封开启力、气膜刚度和泄漏率。由图可知,三个螺旋角对干气密封最优性能存在交互影响,也即当某一螺旋角变化时,最大开启力和最大气膜刚度对应的其他两个螺旋角的优选值也随之变化。当转折螺旋角为10°时,最大开启力、泄漏率和气膜刚度对应的出口螺旋角分别为90°、50°和10°,对应的入口螺旋角分别为50°、50°和10°;随着转折螺旋角的增大,各项密封性能参数最大值对应的出口螺旋角和入口螺旋角都单调递减,且转折螺旋角为30°时对应有最大的开启力和气膜刚度。当转折螺旋角一定时,开启力和气膜刚度随进口螺旋角的变化梯度较大,而随出口螺旋角的变化梯度较小;泄漏率随进口螺旋角和出口螺旋角的变化梯度都较大。 若节点在每个时隙过程中均以独立概率P接入信道,那么可以在退避过程中建立以时隙为单位的离散条件下的二进制退避阶数s(t)和碰撞窗口b(t)的马尔科夫过程[13],如图4所示. 图6 广义螺旋角对广义螺旋槽干气密封性能的影响Fig.6 The influence of generalized spiral angle on the performance of generalized spiral groove seal 为定量探讨上游槽和下游槽侧壁型线形状的影响,分别研究了进口螺旋角、出口螺旋角和超椭圆系数对广义螺旋槽干气密封稳态性能的影响程度。以进口螺旋角和出口螺旋角的影响为例,在给定转折螺旋角和超椭圆系数时,获得进口螺旋角为定值和出口螺旋角在10°~90°范围内变化时干气密封开启力、泄漏率和气膜刚度的平均值及标准差,定义性能参数的均值变化率为给定进口螺旋角范围内性能参数均值最大值与最小值之差与其平均值的比值,其反映了该性能参数对进口螺旋角取值变化的敏感程度,性能参数均值变化率越大,则进口螺旋角影响越显著;标准差可间接反映出口螺旋角对该性能参数的影响程度,标准差越大,则出口螺旋角影响越显著。 图7所示为β2=30°时,进口螺旋角和出口螺旋角对广义螺旋槽干气密封稳态性能的影响。由图可知,随着β1和β3的增大,开启力和泄漏率都先增后减,而气膜刚度则单调递减。入口螺旋角对开启力和气膜刚度影响显著,而出口螺旋角影响则较弱,如β1从10°增至90°时,开启力和气膜刚度的均值变化率分别达到5.5%和35.3%,而当β3从10°增至90°时,对应的均值变化率只有1.5%和11.5%;入口螺旋角和出口螺旋角对泄漏率的影响程度相当,入口螺旋角和出口螺旋角对应的泄漏率均值变化率分别达到6.4%和6.8%。同时,各性能参数随螺旋角变化的标准差也进一步印证了上述结论。 图7 进口螺旋角和出口螺旋角对干气密封稳态性能的影响(β2=30°)Fig.7 The influence of inlet spiral angle and outlet sprial angle on the steady-state performance of dry gas seals(β2=30°) 图8所示为β1=15°、β2=30°、β3=45°,n1和n2在0.1~10取值范围内,上游槽和下游槽超椭圆系数对广义螺旋槽干气密封稳态性能的影响。各性能参数随上游槽超椭圆系数n1的增大都先增后减,近似在n1=1时获得最大值,随下游槽超椭圆系数n2的增大而单调递增。n1对三个密封性能参数影响都较显著,而n2仅对泄漏率的影响较大,而对开启力和气膜刚度影响较小。 11月21日,德州市十八届人大常委会第十六次会议举行联组会议,对德州市获得地方立法权后出台的首部实体性法规——《德州市城乡容貌和环境卫生管理条例》实施情况进行专题询问。联组会上,常委会委员和列席会议的省、市人大代表组成“考官团”,直击民生热点,向城管、交警、规划、交通等部门主要负责人提出了一系列群众普遍关注的问题。 图8 上游槽和下游槽超椭圆系数对干气密封稳态性能的影响(β1=15°、β2=30°、β3=45°)Fig.8 The influence of the hyperelliptic coefficient of upstream and downstream grooves on the steady-state performance of gas seals(β1=15°,β2=30°,β3=45°) 在上述分析的基础上,结合表5所示的不同上游槽和下游槽型线表征参数对应的性能参数均值变化率可看出,上游槽型线形状对各密封性能参数影响都很显著,而下游槽型线形状仅对泄漏率和气膜刚度影响显著,而对密封开启力影响较弱。已有螺旋槽干气密封的设计经验表明,通过螺旋角改变引起开启力增大的同时往往伴随着泄漏率的增大。本文提出的广义螺旋线则为解决该矛盾提供了新的思路,也即通过上游槽型线设计以获得较大密封开启力和气膜刚度,通过下游槽型线设计以重点控制密封泄漏,进而有望在实现高气膜承载力、高气膜刚度的同时获得较低的泄漏率。 表5 不同上游槽和下游槽型线特征参数对应的性能参数均值变化率Table 5 The sealing performance change rate corresponding to the characteristic parameters of the upstream and downstream grooves 进一步探讨不同压力和速度工况下广义螺旋槽与经典对数螺旋槽干气密封的稳态性能优劣,进而探讨不同工况下端面型槽的最佳侧壁型线。在任一压力和速度工况下,广义螺旋槽的三个广义螺旋角β1、β2和β3为10°~50°范围内,每个广义螺旋角等间隔5°取值而获得9个数值,基于完全析因设计方法共计获得729组广义螺旋角数值组合,并从中获得最大开启力、气膜刚度和刚漏比及其对应的广义螺旋角优选值;同理,可获得各压力和速度工况下经典对数螺旋槽干气密封的稳态性能最大值及对应的螺旋角优选值。定义稳态性能增量比为广义螺旋槽干气密封性能参数最大值与经典螺旋槽干气密封性能参数最大值的相对增量。 图9所示为压力0.2~10 MPa、线速度2~100 m·s-1条件下广义螺旋槽干气密封的开启力增量比、气膜刚度增量比和刚漏比增量比。由图可知,在低压高速条件下,广义螺旋槽干气密封的稳态性能增量比较大,而在高压低速条件下较小;进一步,在低压高速条件下,开启力增量比始终小于1%,则气膜刚度增量比和刚漏比增量比有望超过3%,这说明以流体静压为主导的高压低速条件下经典对数螺旋线表现优异,而在以流体动压效应占主导的高速低压条件下则有望通过型线形状的优化获得比经典对数螺旋槽更佳的气膜稳定性和综合密封性能。 图9 不同工况下广义螺旋槽干气密封的性能参数增量比Fig.9 Performance parameter increment ratio of generalized spiral groove dry gas seal under different working conditions 图10为不同优化目标和工况条件下广义螺旋槽和经典螺旋槽干气密封的优选结构。对于经典螺旋槽,随着介质压力增大和速度减小,也即流体静压效应逐渐增强,最大气膜刚度和最大刚漏比对应的最优螺旋角都略有增大,螺旋槽形状逐渐由细长型变为宽短型。对于广义对数螺旋槽,最大气膜刚度对应的最佳进口螺旋角和转折螺旋角都逐渐增大,而出口螺旋角逐渐减小,型槽形状总体呈现出先扩后缩状,如表3“先扩后缩槽”所示;最大刚漏比对应的广义螺旋槽在低压高速时与经典螺旋槽差异不大,而在高压低速时表现为流道逐渐变窄的“流道渐缩槽”,类似于斜直线槽。 图10 不同目标函数和工况条件下两种螺旋槽的优选结构Fig.10 Optimal structure of two spiral grooves under different objective functions and working conditions 总体而言,经典对数螺旋槽干气密封在各压力和速度工况下表现优异,单纯通过型线形状的优化难以获得密封性能的显著提高。不过转折螺旋角较进口螺旋角、出口螺旋角更大的流道先扩后缩槽干气密封有望获得更大的气膜刚度。 端面型槽侧壁结构是由广义螺旋角分布和型线周向偏转角度共同决定,如图1所示的雁型槽和双叶翼型槽都是通过上、下游槽之间迎风侧或背风侧型线的周向偏转以实现对气流通道形状的调控。探究型槽型线周向偏转对广义螺旋槽干气密封稳态性能参数的影响,并获得最大开启力、气膜刚度和刚漏比对应的最佳型槽结构。 显而易见的是,因型线周向偏转改变了型槽的周向结构,相同优化目标下不同型槽结构对应的最佳周向槽宽比也各不相同,而只有将不同结构型槽的最佳性能相比较才更有意义。为分析方便,下文的广义螺旋槽中侧壁型线仍为经典对数螺旋线。图11所示为周向槽宽比对经典螺旋槽和一种典型广义螺旋槽(雁型槽)干气密封开启力和气膜刚度的影响。由图可知,不同性能参数和型槽结构对应的最佳周向槽宽比各不相同,如最大开启力和气膜刚度对应的经典螺旋槽最佳槽宽比分别为0.60和0.45,而对应的广义螺旋槽最佳槽宽比则分别为0.85和0.80。进一步,将雁型槽和螺旋槽的最大开启力和气膜刚度比较发现,前者的最大开启力和气膜刚度均有所减小。 因超声波具有强的指向性、缓慢的能量消耗速度、在媒介传播距离远的特性,因而测距系统常采用超声波技术。测量距离利用超声波技术,具有设计简便、计算方法简单、测量精度达标的特点。超声波测距系统结构简单,安装方便,相对于其他测距方式更适用于煤矿原煤仓的工作环境。 图11 周向槽宽比对雁型槽和螺旋槽干气密封性能的影响Fig.11 Optimal structure of two spiral grooves under different objective functions and working conditions RF——开启力增量比,% 干气密封的开启力、气膜刚度和泄漏率是其设计时需重点关注的三个参数:密封开启力和闭合力的平衡决定了密封平衡膜厚值,在相同的膜厚下期望有更大的密封开启力以实现更好的动压开启特性及气膜承载能力;气膜刚度和泄漏率反映了干气密封抵抗轴向扰动和控制介质泄漏的能力,更大的气膜刚度和更小的泄漏率意味着更好的气膜稳定性和密封性,故往往采用刚漏比(气膜刚度与泄漏率之比)这一参数作为表征干气密封稳定性和密封性的综合参数。干气密封开启力Fo、气膜刚度kz、泄漏率q和刚漏比Γ可用以下公式计算: 图12 高速低压下型线周向偏转对干气密封性能的影响Fig.12 The influence of circumferential deflection on the performance of dry gas seal at high speed and low pressure 图13 高压低速下型线周向偏转对干气密封性能的影响Fig.13 The influence of circumferential deflection on the performance of dry gas seal at high pressure and low speed (1)基于将型槽边界型线沿径向若干等分且每一微段型线可视为对数螺旋线的思想,推导了一种描述型槽边界的广义对数螺旋线几何方程,其对型线几何形状表征能力显著增强;通过设置迎风侧和背风侧型线周向偏转角参数,使其可统一表征不同几何型线和结构形状的端面型槽。 (2)端面型槽上游侧壁型线形状对干气密封开启力、气膜刚度和泄漏率均有显著影响,而下游侧壁型线形状仅对泄漏率和气膜刚度影响显著。 (3)经典光滑对数螺旋槽是一种流体动静压效应强的端面结构,单纯通过改变型线形状或型线周向偏转难以有效提高对数螺旋干气密封的气膜承载力。 (4)为实现干气密封气膜刚度和刚漏比的提高,在低压高速条件下可通过将型槽设计成转折螺旋角较进口和出口螺旋角更大的先扩后缩槽结构,而在高压低速条件下可将迎风侧和背风侧型线都逆向偏转形成折线槽结构。 符号说明 Fo——开启力,N hg——螺旋槽槽深,μm h0——气膜厚度,μm kz——气膜刚度,N·m-1 Ng——螺旋槽开槽数 n1,n2——分别为上、下游型线超椭圆系数 青岛市市北区登州路可以称作“青岛啤酒一条街”,这条街两侧有多家悬挂着各式各样“青啤原浆”霓虹灯箱、“青岛啤酒”广告招牌的饭店酒吧,它们或许都因为毗邻着已有115年历史的青岛啤酒厂而生意兴隆。旺季时,青岛啤酒博物馆的品酒区一天就能接待7000人尝鲜青啤原浆。 pi——内径侧压力,MPa po——外径侧压力,MPa q——泄漏率,m3·s-1 在迎风侧和背风侧偏转角系数取值范围为-0.5~0.5时,取不同数值的α1和α2组合以获得不同结构的广义螺旋槽结构,取各结构型槽干气密封的开启力、气膜刚度和刚漏比最大值进行对比以探讨不同工况参数和优化目标条件下的最佳型槽结构。图12和图13所示分别为高速低压(po=0.5 MPa,v=100 m·s-1)和高压低速(po=5 MPa,v=5 m·s-1)条件下迎风侧偏转角系数α2和背风侧偏转角系数α1对干气密封稳态性能参数最大值的影响,其中α1=α2=0时为经典光滑对数螺旋槽结构。在高速低压条件下,通过型线周向偏转获得的开启力和气膜刚度较经典光滑螺旋槽干气密封相比增量很小。在高压低速条件下,经典光滑螺旋槽干气密封具有最大的开启力,说明光滑对数螺旋槽是一种流体动静压效应强的结构;然而,α1>0且α2>0的干气密封能获得显著更大的气膜刚度和刚漏比,相较于光滑螺旋槽干气密封的增幅分别为15.6%和10.6%,且优选值为α1=0.4和α2=0.3。 Rk——气膜刚度增量比,% 3)春季低空切变和地面倒槽是引发暴雨最重要的影响系统。夏季各月的主要影响系统存在较大的差别,6月份最常见的天气系统配置是高空槽东移,中低层有切变或急流配合,地面有倒槽或低压存在,另外6月时东北冷涡与地面倒槽或低压的配合也是典型的系统配置,此时低空急流的强度在一定程度上影响着降水量的大小。7月的暴雨过程主要受到副高和台风的影响。8月份台风引起的暴雨天气过程频数明显增多。秋季的暴雨主要是秋台风导致。 RΓ——刚漏比增量比,% rg——密封端面槽根半径,mm rh——密封端面转折半径,mm ri——密封端面内径,mm 求解式(16)的强制性压力边界条件为: ro——密封端面外径,mm v——密封端面平均线速度,m·s-1 α1,α2——分别为背风侧、迎风侧偏角系数 β——螺旋角,(°) β1,β2,β3——分别为入口、转折和出口螺旋角,(°) β1j,β2j——分别为上游槽和下游槽广义螺旋角,(°) Γ——刚漏比,N·s·m-1 γ1——径向槽长比 γ2——上游槽长比 δ——周向槽宽比 μ——气体黏度,mPa·s θg——槽根周向夹角,(°) θh——开槽区周向夹角,(°) θ1——背风侧偏转角,(°) θ2——迎风侧偏转角,(°) θ1,j,θ2,j——分别为背风侧和迎风侧在任意半径rj处的极角,(°) Δθj——任意微段型线对应周向夹角,(°) ε——收敛残差 κ——收敛因子
1.2 广义螺旋槽的几何表征能力
1.3 密封性能求解数学模型

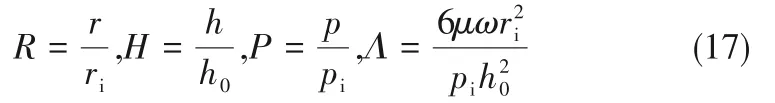

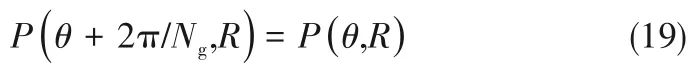
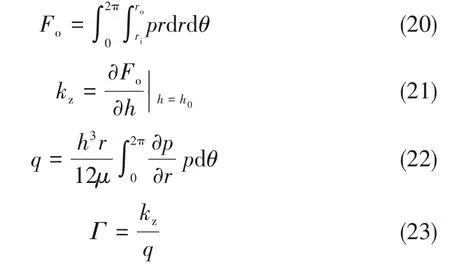
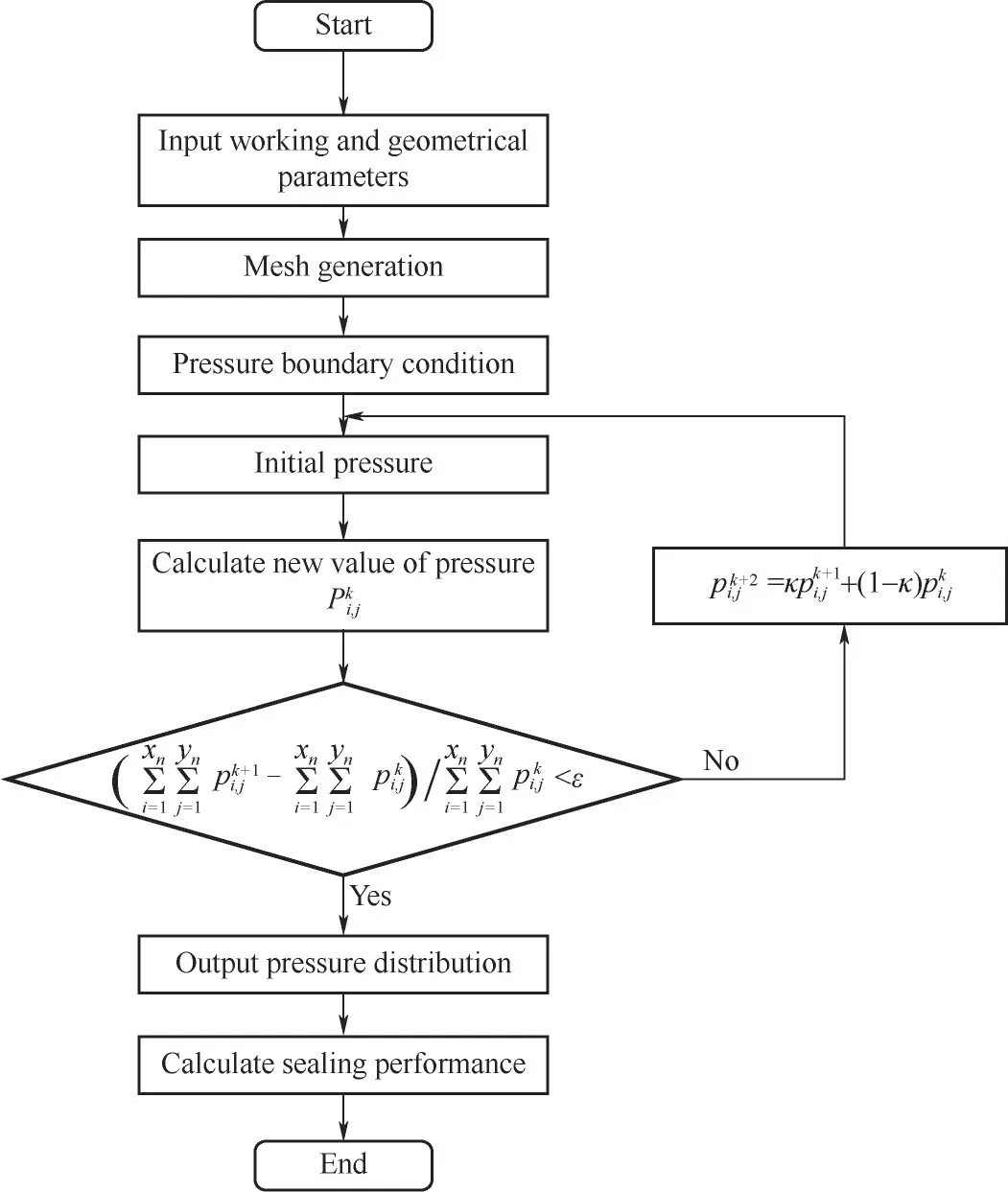
2 结果讨论与分析

2.1 径向分段数影响

2.2 给定工况下广义螺旋角影响


2.3 不同工况下广义螺旋角分布影响
2.4 型线周向偏转对干气密封性能影响
3 结 论
