Control of firing activities in thermosensitive neuron by activating excitatory autapse∗
2021-10-28YingXu徐莹andJunMa马军
Ying Xu(徐莹) and Jun Ma(马军)
1School of Mathematics and Statistics,Shandong Normal University,Ji’nan 250014,China
2Department of Physics,Lanzhou University of Technology,Lanzhou 730050,China
3School of Science,Chongqing University of Posts and Telecommunications,Chongqing 430065,China
Keywords: thermosensitive neuron,autapse,firing pattern,bifurcation
1. Introduction
The brain contains many function regions due to the diversity in function of neurons and connections to astrocytes.The reveal of the mystery of cognitive neural principles in the brain can provide a good insight into the potential mechanism for information transmission, encoding and processing by exploring the dynamics of neural activities in the brain.Therefore,it is critical to obtain a reliable biophysical neuron model,[1–3]and thus the effect of anatomic structure,biophysical activities can be considered completely. Besides the conventional physiological experiments,the brain function imaging, reliable theoretical analysis and numerical approach are effective to judge the information transmission and processing in nervous systems. Neurons are the basic unit for information processing in brain and different biophysical functions are trained and enhanced in different neurons. Most of the neurons have the intrinsic properties such as excitement and conduction,and thus external stimulus can be encoded and propagated between neurons. Within most of the generic neuron models, bifurcation parameters, and external forcing current can be adjusted to trigger different firing patterns and mode selection in the neural activities.[4–8]Also, external stimuli can be used to detect possible occurrence of nonlinear resonance(stochastic resonance and coherence resonance).[9–13]Furthermore, these neuron oscillators are often used to build neural network with different topologies,and the collective behaviors such as wave propagation and stability,pattern formation,synchronization stability can be further investigated.[14–17]The network can present regular spatial distribution under selforganization by taming the local kinetics and coupling channels in the network. On the other hand, many nonlinear circuits can be tamed to reproduce similar firing patterns generated from biological neurons,and thus neural circuits[18–21]are obtained. When more functional electronic components such as memristor, Josephson junction, thermistor, phototube are incorporated into the neural circuits, they can be tamed to percept the effect of field memory, magnetic field, temperature, and external optical illumination by generating equivalent channel current across these functional components.[22–25]As a result, the involvement of more functional components in the artificial network composed of micro neural circuits throws light on the realization and application of intelligence and treatment in nervous disease by repairing neural pathways with auxiliary neural network.
Synapse can receive,encode and propagate electric signal effectively. Electric synapse can be activated to establish the connection between neurons and gap junction coupling,[26,27]and the synaptic current is changed rapidly to balance the membrane potential. Chemical synapse changes its synaptic current when the neurotransmitter is released, and biologists claimed that chemical synapses[28–31]play main roles in signal exchange and propagation between neurons. From physical viewpoint,electric synapse coupling is similar to the voltage coupling via resistor connection,the gap junction between synapses can generate equivalent resistance as resistor. While chemical synapse coupling can induce field coupling[32–34]during the release and propagation of extracellular and intracellular ions of the cell. When more neurons are connected to build networks, electric synapse, chemical synapse and even hybrid synapse can be activated to couple neurons for estimating the synchronization stability,wave propagation and pattern selection. Autapse is a specific synapse,[35]which reconnects its body or muscle,and it is claimed that the formation of autapse results from self-healing in injured neurons by building an auxiliary loop.[36]Such as the firing frequency of spiking behaviors near sub-critical Hopf bifurcation can be reduced by a short-term delayed excitatory autapse. Meanwhile,the study found an abnormal phenomenon, that is, inhibitory autapse can induce the resting state to change into a stable spiking pattern.[37,38]It often takes a certain response period when external stimulus is encoded to change the dynamical behavior of nonlinear oscillators. The involvement of autapse in neurons can introduce time delay,and this additive bifurcation parameter has a distinct effect on the dynamics of neurons connected to autapse.[39]Indeed, the activation of autapse can generate time-delayed feedback and its self-adaption of neurons can be enhanced. Furthermore,local pacing and heterogeneity can be induced to generate continuous pulse, wave fronts and even defects when local area of the neural network is driven by autapses.[40,41]That is, local distribution of autapses can regulate the collective behaviors of neural network by generating stable pulse or wave fronts.
It is interesting to understand the communication mechanism between finite neurons in order to study the information transmission and information processing in neural networks. The neural firing activities and the chemical activities of synapses between neurons are involved in information processing.[28,29]The neural activities can be identified by resting state subthreshold oscillation,spiking,bursting,and chaotic firing.[42–44]In 1952, Hodgkin and Huxley proposed the famous Hodgkin–Huxley neuron model based on physiological experiments,[1]and then more improved neuron models were further proposed.[45–47]For example, based on the Morris–Lecar neuron model, the half activation potential parameters of the potassium activation curve are determined,and the properties of the membrane can be controlled by changing the value of a single parameter.[2]Recently, the subthreshold vibrational resonance and the superthreshold vibrational resonance in the FitzHugh–Nagumo (FHN) neuron model were investigated.[3]The nervous system makes local heterogeneity in the network due to complex connection graph and diversity in parameters. Therefore, it is a challenge to obtain reliable neuron models so that specific biophysical effects can be estimated and considered. For example, the fractional order model,[48]the electromagnetic radiation driven model,[49]and the light-dependent neural model[50]have been suggested to estimate the memory effect,electromagnetic induction and encoding in visual system under illumination. In particular,the involvement of memristor into the neural circuit can explain the activation of memristive synapse and physical mechanism of field coupling between neurons.[51–53]In fact, the feedback coupling,[4]non-local coupling,[54]time delay,[5–7]and external stimuli[8]can affect the dynamic behaviors of the nonlinear systems. The bifurcation direction and the stability of oscillation state are changed by reducing noise intensity or increasing natural frequency heterogeneity.[55]In the case of synchronization between nonlinear circuits and neurons, the optimization of coupling channels can enhance the synchronization stability. For example, a hybrid synapse is activated to synchronize two Fitzhugh–Nagumo neurons driven by two voltage sources.Moreover,induction coil coupling can benefit the realization of synchronization between two chaotic Chua systems[56]by balancing the energy pumping along the coupling channels.
The inherent time delay should be considered in the process of information transmission. The response time delay accounts for the delay in encoding external stimuli, while the propagation time delay is generated by the signal transmission between neurons. In fact,some experiments on inter-neurons have proved that time delay can enhance the adaptability of neurons to external stimuli.[57,58]In the neural networks, local dynamics and connection types are important for regulating synchronization stability,and the release of collective behaviors. However, neural energy may be an effective tool for studying the overall behavior of brain activities,[59]and also for using a finite amount of neural energy to obtain the most efficient spatial information representation of the spike positions organized in the available environment.[60]In addition,neural coding and impulsive effects are attractive questions in the field of neurodynamics.[61]For instance, the couplingpair number density is used as the distributed coding mode for neuronal network to study the effects of external stimuli and noise on the dynamics of neuronal oscillator networks.[62]Furthermore,neurons can form various functional connection loops and perform computational functions through synaptic connections.[63]As mentioned above, the autapse is widely found in cerebral cortex, visual cortex, cerebellum, striatum,and hippocampus,[39]and it has a certain effect on the ability of neurons to detect weak signals.In addition,the autaptic current plays a wide role in regulating the discharge rhythm of a single neuron and the nonlinear behavior of the network. The involvement of autapse connection provides some evidences to confirm the bifurcation role of time delay on dynamics of nonlinear systems.[64,65]
In previous researches the neuronal dynamics was studied at constant temperature. However, membrane potential is not only regulated by external stimuli, but also sensitive to the temperature because of its changes in the activation of ion channels and excitability. The reaction rate of biochemical reaction is affected by temperature,including the activation and inactivation of membrane ion channels, the activation and release of synapses,the release and conduction velocity of nerve impulses.[66]Some evidences have confirmed that the duration of the pulse decreases with the diaphragm temperature increasing.[11]Previous experiments have shown that temperature affects the conversion rate between opening and closing of ion channels,so temperature factor is introduced into the kinetic constants of ion channels.[67]Braunet al.[68]proposed a thermosensitive neuron model that mimics all spike train patterns observed in electroreceptors from dogfish catfish,and facial cold receptors.Zhaoet al.[69]investigated the BZ reaction oscillation wave from the time-lapse imaging data,embedded the reaction temperature which influences the diffusion coefficient into a pure mathematical model,and finally constructed the temperature dependent FitzHugh–Nagumo model. Furthermore, the authors of this paper ever suggested that thermistor can be incorporated into neural circuits for estimating the temperature effect on mode selection in neural activities. The typical characteristic of thermistor is that the resistance value is sensitive to temperature changes.[70]Coupling the thermistors into a simple FHN neural network circuit enhances the physical function of the circuit. The channel current across the thermistor is changed by the temperature, and it reproduces the main dynamic characteristics of biological neurons by generating different firing patterns.[12]Thermistors can be connected to the appropriate branch in nonlinear circuits and thus its dependence on temperature change[13]can be enhanced Here,both autapse and thermistor are introduced into a simple neural circuit,and the mode selection is explored to know the biophysical processing in neural activities.
2. Model and scheme
In 1926, Van der Pol[71]proposed the simplest model,which was derived from the nonlinear relaxation oscillator.Furthermore,Fitzhugh[46]and Nagumoet al.[47]presented its mathematical form of excitable neurons, and its dynamical equations are given as follows:

wherexandydenote the fast variable and slow variable of the nervous system, respectively, and the dynamics is dependent on the membrane potentialxand recovery variabley;a,b,c,andµare the normalized parameters;Iusis the external forcing current. By adjusting these parameters, the neuron oscillator can be triggered to display quiescent, spiking, bursting, and chaotic firing patterns. This neuron oscillator can be implemented in nonlinear circuit composed of capacitor,inductance coil,constant voltage source,and nonlinear resistor.As is well known,negative temperature coefficient(NTC)thermistor has been found wide applications in temperature measurement,temperature compensation of electronic components, current,and voltage limiters. It is suggested[70]that the NTC thermistor can be used for the synchronization and control of chaotic circuits, and its physical property of temperature dependence is estimated by
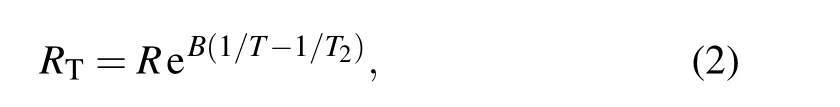
whereRTrepresents the resistance of the thermistor at temperatureT,andRdenotes the nominal resistance of the thermistor at the rated temperatureT2. TheRis considered as a constant at an infinitely high temperatureT2→∞(i.e.,when 1/T2→0).TheBis the thermal index,indicating the material constant of the thermistor, which depends on the ratio of the activation energyqto the Boltzmann constantk. The neural circuit is dependent on the temperature when a linear resistor is replaced by a thermistor. By applying the scaling transformation to the physical variables and parameters for the nonlinear circuit,the temperature-dependent neuron oscillator driven by autapse is obtained by
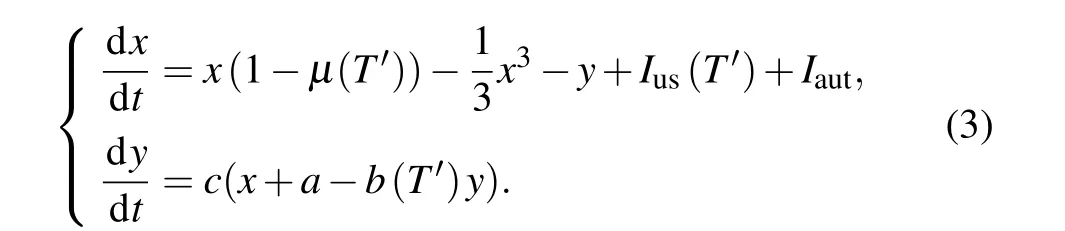
The normalized parameterT′=T/T0is a dimensionless temperature variable,whereTis the physical temperature andT0is the room temperature. Based on Eq. (2), the dimensionless parameters can be expressed asµ(T′)=µ0exp(−1/T′),Ius(T′)=Iusexp(−1/T′),andb(T′)=b0exp(1/T′). Furthermore,the chemical autapse is connected to the neural circuit,and the autapstic currentIaut, which is described by the fast threshold modulation scheme,[30]is defined by

whereHrepresents the coupling strength of chemical autapse;τis the time lag,which denotes the finite time required for the signal to travel along the axon and return to the neuron itself;VposandVprerefer to the post-synaptic and pre-synaptic membrane potentials, respectively;Vsynis the reversible potential,which the excitatory autapse and inhibitory autapse depends on. IfVsynis greater than the resting potential of a single neuron, the autapse is excitatory, otherwise, it is inhibitory autapse. The parameterθrepresents the synaptic threshold,andσis ratio constant.
3. Results and discussion
In this section,the fourth order Runge–Kutta algorithm is adopted to find numerical solution for the functional neuron in time steps of 0.01. The initial values of the two variables in Eq. (3) are selected to be 0.1 and 0.3. The parameter values for the system area=0.8,c=0.1,Vsyn=2,θ=−0.25,σ=10.[18]In order to study the influence of autapse on the action potentials of thermosensitive neurons,it is necessary to ensure that the system is in an oscillatory state. That is,to determine the external forcing current that can cause the system to appear in a limit cycle, the spiking dynamics of the FHN neuron model without autapse connection is calculated, and the results are shown in Fig.1.

Fig. 1. (a) Time evolution of membrane potential x at Ius =0.5, (b) phase portrait Ius =0.5, and (c) bifurcation curve for the maximum (black solid square)and minimum(red solid square)values of x versus Ius,with parameters selected to be a=0.8,c=0.1,b=0.7,andµ=0.175,and no autapse driving considered in calculations.
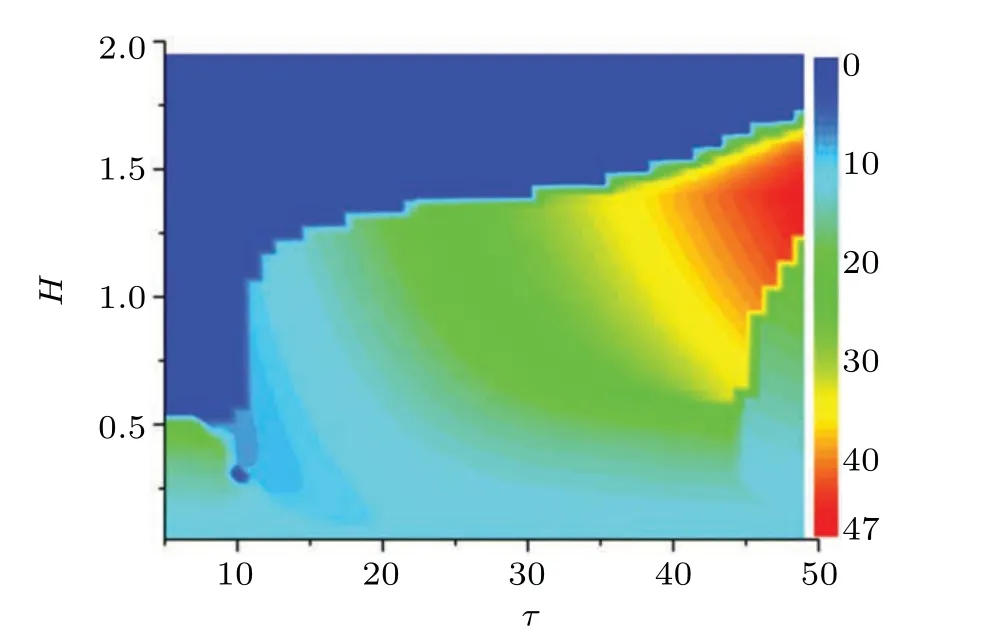
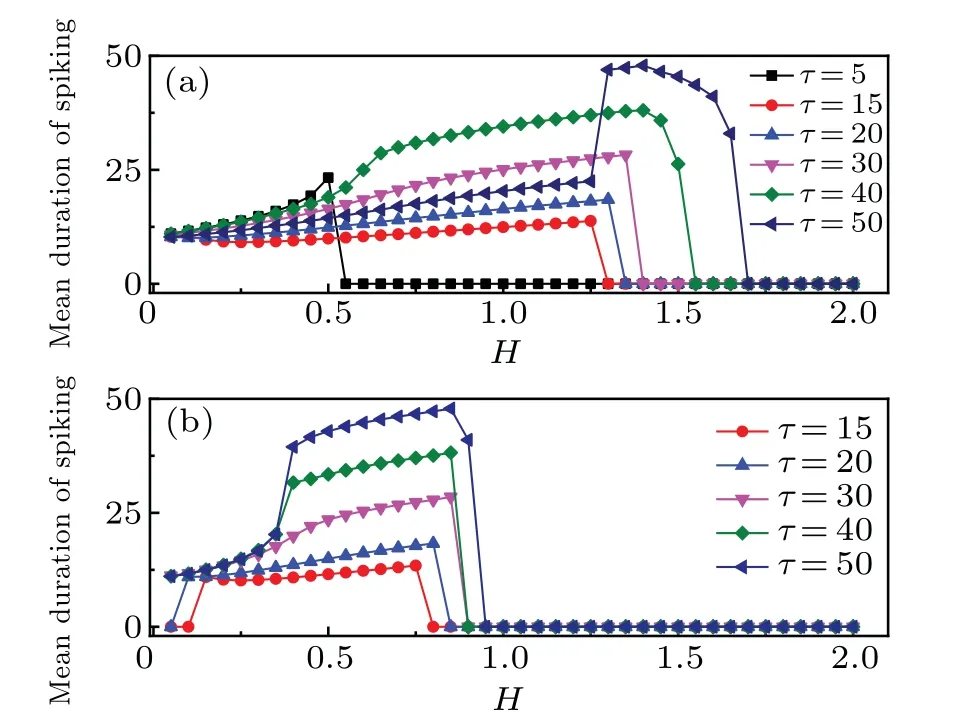
The membrane potential is affected by the external stimuli,and the firing mode can be adjusted for generating periodical oscillation without autapse driving. Obviously,for larger or smaller external forcing currentIus,the system is in a resting state, and only in the range of 0.4 Confirmed in Fig.2(a)are that the temperature has a great influence on the dynamics of thermosensitive neurons, and that the firing pattern is controlled by temperature completely when other parameters are fixed. The neural activity changes from resting state to periodic oscillation as the temperature increases. When the temperature is less than 5.49, there is a stable solution in this system,and the resting potential is measured with the external forcing currentIus=0.5. That is,neurons are more excitable at moderate temperatures. However,whenT′is greater than 5.49,the amplitudes of membrane potential keeps invariant with the increase of temperature while the ISIs decreases with temperature increasing. The average firing frequency increases with the temperature increasing,and this occurrence becomes distinct when the temperatureT′is lower. After a sharp decrease in ISIs, the curve becomes flat because the sensitivity of firing mode to temperature is weakened. Under high temperature, the amplitude of the firing is reduced, and the number of firings seems to be big, but the duration and height of the firing pattern are very low,and the firing pattern is no longer a spiking pattern. Therefore,only at the optimal temperature can the firing mode carry the neuron information well. The results in Ref.[26]show that the duration of the pulse decreases with temperature increasing. The simulation results are consistent with the experimental results,that is,the average duration of the membrane voltage pulse decreases when the temperature is further increased as shown in Fig.2(b). Autapse is a self-synapse,in which there exists a connection between a neuron and itself. With the increase of autaptic time lagτof the autapse, the ISIs of firing patterns increase periodically. When the temperature is considered in the improved FHN model,asτis increased to 62,the firing regularity is destroyed. Surprisingly, whenτis further increased to 75,the spiking behavior once again becomes more regular and dense as indicated in Fig.3. Fig. 2. (a) Curve of maximum value (black solid square) and minimum value (red solid circle) of x versus T′, and (b) bifurcation diagram of ISIs varying with temperature T′,with parameters selected to be a=0.8,c=0.1,b=0.7, µ =0.175,and Ius =0.5 in the improved FHN model without autapse driving. Fig. 3. (a) Improved FHN model without temperature and (b) improved FHN model with temperature T′=10 versus τ with parameters selected to be with b=0.7,µ =0.175,Ius=0.5,and autaptic intensity H=0.3. Furthermore,the autapse connection is activated,and the chemical autaptic current is released to excite the thermosensitive neuron. The changes of ISIs are calculated by adjusting the intensity of autaptic current with constant time delay,then the dependence of time delay in the autapse is presented for possible contrast,and the results are depicted in Fig.4.Technically,the thermosensitive neuron generates spikes under a certain external forcing current, and then it injects a small pulse to postpone or hasten the spiking. Indeed, both of intensity and time delay in the autapse have distinct effect on the firing patterns and oscillation mode in the neural activities. The results in Fig.4 demonstrate that forT′=10,asHchanges from 0 to 0.6,the ISIs fluctuate significantly. When no delay in autapse is considered,the autaptic intensity and temperature have the same effect on neuronal discharge,that is,both of them reduce the interspike intervals of membrane potential. At a specific autaptic intensity,the ISI reaches the lowest value and the firing frequency of neurons reaches the highest point as indicated in Fig. 4(a). However,the increase in time lag breaks this occurrence. The ISI of the neuron presents a certain increase and then decreases with autaptic intensity increasing. WhileHis in the range from 0.3 to 0.335,the membrane potential is below zero,and it is classified as a resting state. Whenτis increased to 50 andHis less than 0.07, the firing regularity is destroyed. With the increase of autaptic intensity, the ISI curve changes smoothly.This means that the selection of firing mode is more sensitive to smaller synaptic strength under the longer delay time. Extensive numerical results are presented to identify the firing modes by taming the parameters for the chemical autapse,and the results are shown in Fig.5. Fig.4. Bifurcation diagram of ISIs varying with autaptic intensity H under different time lags τ at Ius=0.5,T′=10,and τ =0(a),10(b),50(c),and 100(d). Fig.5. Spike trains of improved FHN model with autapse,calculated under Ius=0.5 and T′=10,at(a)τ =0 and H=0.3;(b)τ =10 and H=0.25;(c)τ =10 and H=0.3;(d)τ =50 and H=0.05;(e)τ =50 and H=0.08;(f)τ =100 and H=0.6. It is found that the firing patterns of neurons depend on autaptic current,which has different time lags and autaptic intensities. At the same time, in order to observe the influence of temperature on the statistical properties of the membrane potential,the maximum values and minimum values of pulses increase with temperature rising under a certain autaptic current are calculated as shown in Fig.6. Forτ=10 andH=0.3,whenT′changes from 0 to 40,the bifurcations are different from those in Fig.2,as shown in Fig.6.The improved FHN model without autapse exhibits one bifurcation point as the temperature changes forIus=0.5. For the improved FHN model with autapse,excitatory autapse can also induce system bifurcation. Interestingly, when the temperature is less than 5.49,the system has a limit cycle withT′changing. At the beginning,there is only a stable equilibrium point in the system, and the membrane potential of neurons converges to a fixed value after time evolution. As the temperature increases to the bifurcation pointT′=1.5,the membrane potential of neurons presents a periodic discharge. WhenT′rises to 2.5,the limit cycle disappears and the system has only one stable state as shown in Figs.6(c1)and 6(c2). In the range of 7 to 11.5, the neurons show small amplitude periodic oscillations, which are illustrated in Figs.6(d1)and 6(d2). Stable periodic oscillations are observed when the temperature is greater than 11.5. The amplitude of membrane potential does not change when the temperature increases to a certain extent.Note that this result is similar to that of the system without autapse in Fig.2. That is to say, excitatory autaptic can change the firing pattern of neurons. At an appropriate temperature,neurons are promoted to produce action potential by excitatory autaptic stimulation. In order to observe the effect of temperature on the statistical properties of membrane potential, the variations of mean duration of spiking with temperature at different autaptic intensities are shown in Fig.7. Fig.6. (a)Bifurcation diagrams of xmax and xmin for improved FHN neuronal model versus temperatures,(b1)x–t and(b2)y–x at T′=2,(c1)x–t and(c2)y–x at T′=5,(d1)x–t and(d2)y–x at T′=10,and(e1)x–t and(e2)y–x at T′=20,with other parameters being τ =10,H=0.3,and Ius=0.5. Figure 7 shows the variations of average duration of the membrane potential with temperature, where different colors indicate different autaptic intensities. The duration of a spiking can be defined as the time required for the action potential to drop from greater than 0 mV to−0.5 mV, for the differences among thresholds have no qualitative influence on the results. It can be seen from the figure that the simulation results are consistent with the experimental results, that is, the average duration of the membrane potential decreases as the temperature increases.[67]The increase of temperature leads the channel opening time to decrease,which is consistent with the experimental result in the recent literature,[12]that is, the channel opening time is increased by reducing the temperature. The results show that the firing duration of neurons can be affected by the autaptic intensity. The injected autaptic current is positively correlated with the duration of the action potential.However,when the temperature is in a lower range,the autapses can well regulate the firing patterns of neurons. The average duration of pulses is sensitive to autapse connection,so the autapse plays an important role in regulating the neuronal signal processing as described in Ref. [39]. The magnitude of the autaptic current injected into the neuronal system depends not only on the autaptic intensity,but also on the time lag. The mean inter-spike intervalversustemperature is calculated to investigate the effect of time lag on membrane potential. Fig.7. Variations of mean duration of spiking with temperatures under different autaptic intensities when τ =30. Figure 8 shows the variations mean inter-spike interval of membrane potential with temperatures at different time lags,which are used to elucidate the effect of autapse in the improved FHN model.The mean inter-spike interval of the membrane voltage pulse is positively correlated with temperatures,and the trend of the curve is opposite to that of Fig.7.It is suggested that the increase of temperature promotes the increase of firing frequency of neurons. The firing frequency of neurons can be promoted by increasing the time lag.However,the mean inter-spike interval first decreases and then increases in a certain temperature range atτ=40. To study the regulation mechanism of autapse on membrane potential of thermosensitive neuron, the mean duration of spiking under different autaptic intensities and time lags is calculated in Fig.9. Fig.8. Variations of mean inter-spike interval with temperatures for different time lags at autaptic intensity H=0.4. At a certain temperature, the mean duration of spiking value is longer,indicating that the discharge frequency of neurons is higher. As can be seen from Fig.9,the time lag starts from 15,and the autaptic intensity and time lag are positively correlated with the frequency of neurons. It is worth noting that for the temperature fixed at 10,the influence of the autaptic intensity on the mean duration of spiking is nonlinear when theτis equal to 1.That is,the mean duration of spiking is sensitive to autapse,but it depends on the temperature. Figure 10 plots the mean durations of spiking varying with autaptic intensity at different temperatures. Fig.9. Variation of mean duration of spiking with τ at temperature T′=10 under different autaptic intensities and time lags,with color-scaled autaptic intensity shown on right side. Figure 10 shows all curves of mean duration of spiking first rise and then decrease with the increase of autaptic intensity. The results show that the generation of action potential is promoted under an appropriate autaptic intensity.The increase of temperature is conducive to the mean duration of spiking to peak at a smaller autaptic intensityH. And the peak value of the curve mainly depends on the time lag, and the effect of temperature can be ignored. However, temperature can promote the neurons to reach the peak at lowerH. The results show that the autapse regulates the firing of thermosensitive neurons,and the firing of thermosensitive neurons can be promoted by autaptic imtensity and time lag in a certain range.Meanwhile, with the increase of temperature, the system can be changed from a resting state to an oscillation state when the time lag is equal to 5. Fig. 10. Variations of mean duration of spiking with autaptic intensity for different time lags at T′=10(a)and 2(b). In summary, the involvement of autapse connection can enrich the mode selection and transition in the neural activities, and it indicates that the temperature-induced firing pattern can be balanced and controlled by autaptic current. As is well known, the astrocyte plays an important role in regulating the neural activity,[71–73]therefore,this study can extended by building astrocyte-coupled functional neurons and network,the occurrence of multiple mode and switch between different firing modes can be more attractive. In this paper, an improved thermosensitive FHN neuron model is used to investigate the effect of autapse driving on neural firing activities. Firstly,the bifurcation diagram of isolated FHN neuron with external stimulus is calculated to detect the parameter region for periodic oscillations. By adjusting the external forcing currentIus, the membrane potential can be changed from the resting state to the periodic discharge state, whenIusis increased continuously, and the resting potential of neurons will be restored. In general,the ion channel or membrane is studied under a constant temperature. However, the dynamics of neurons is not only regulated by membrane voltage,but also dependent on membrane temperatures.The effect of temperature on the membrane potential of neurons without autapse is checked. Temperature change affects the rate of biochemical reactions,including the activation and inactivation of membrane ion channels, the activation and release of synapses, and the conduction velocity of action potential. The spontaneous action potentials can be generated in the improved neuron model at an appropriate temperature,and the average duration of the membrane voltage pulse decreases with temperature increasing as indicated in Fig.2.The previous results show that the duration of the pulse decreases with temperature increasing,and it is confirmed in Fig.2,that is,lowering the temperature can increase the channel opening time. Autapse is a special kind of synapse,which has the ability to regulate the firing pattern of neurons and participates in the information coding process in the nervous system. The existence of excitatory autapse is confirmed, and its function and characteristics are detected in the recent researches. In addition, the autaptic time delay plays an important role in regulating neuronal firing. Therefore, we investigate the potential mechanism of synaptic changes in firing patterns,especially in thermosensitive neurons. By calculating the mean inter-spike interval and the mean duration of spiking,we find that the electrical activity of thermosensitive neurons can be regulated by autapse,and the firing of thermosensitive neurons can be promoted by autaptic intensities and time lags in a certain domain.With the longer delay time, the choice of discharge mode is more sensitive to the smaller synaptic strength. Temperature can promote the neurons to reach the maximum mean duration of spiking under small autaptic intensities. The results of this study provide a new approach to the potential function of excitatory synapses and the regulation of neuronal firing frequency,and can also arouse the interest in further investigating the effects of time delay and temperature on the dynamics and controlling high-dimensional small-world networks.[74–76]






4. Conclusions and discussion
猜你喜欢
杂志排行
Chinese Physics B的其它文章
- Physical properties of relativistic electron beam during long-range propagation in space plasma environment∗
- Heterogeneous traffic flow modeling with drivers’timid and aggressive characteristics∗
- Optimized monogamy and polygamy inequalities for multipartite qubit entanglement∗
- CO2 emission control in new CM car-following model with feedback control of the optimal estimation of velocity difference under V2X environment∗
- Non-peripherally octaalkyl-substituted nickel phthalocyanines used as non-dopant hole transport materials in perovskite solar cells∗
- Dual mechanisms of Bcl-2 regulation in IP3-receptor-mediated Ca2+release: A computational study∗
