Dual mechanisms of Bcl-2 regulation in IP3-receptor-mediated Ca2+release: A computational study∗

Hong Qi(祁宏) Zhi-Qiang Shi(史志强) Zhi-Chao Li(李智超) Chang-Jun Sun(孙长君)Shi-Miao Wang(王世苗) Xiang Li(李翔) and Jian-Wei Shuai(帅建伟)

1Complex Systems Research Center,Shanxi University,Taiyuan 030006,China

2Shanxi Key Laboratory of Mathematical Techniques and Big Data Analysis on Disease Control and Prevention,Shanxi University,Taiyuan 030006,China

3School of Mathematical Sciences,Shanxi University,Taiyuan 030006,China

4Department of Physics and Fujian Provincial Key Laboratory for Soft Functional Materials Research,Xiamen University,Xiamen 361005,China

5State Key Laboratory of Cellular Stress Biology,Innovation Center for Cell Signaling Network,and National Institute for Data Science in Health and Medicine,Xiamen University,Xiamen 361005,China

Keywords: Ca2+,Bcl-2,bifurcation analysis,oscillations

1. Introduction

Calcium ion (Ca2+) is a highly versatile signaling molecule in the cell. It can control many important physiological processes and so is necessary for cell survival.[1,2]Under resting conditions,most of the Ca2+in the cell is stored in the endoplasmic reticulum (ER), and cytosolic Ca2+concentration ([Ca2+]) is maintained at low levels. The homeostasis of[Ca2+]is dynamically regulated by active Ca2+uptake through sarco/endoplasmic reticulum Ca2+-ATPase(SERCA)and passive Ca2+leak from the ER.Upon stimuli,IP3(inositol 1,4,5-trisphosphate)forms and binds to IP3receptor(IP3R)to release Ca2+from the ER,generating the upstroke of a Ca2+oscillation. The SERCA then pumps the released Ca2+back into the ER, completing the Ca2+oscillation.[3]The resulting Ca2+oscillations display different amplitudes and periods,thereby regulating different cellular functions.[3]However,excessive elevations of [Ca2+] always trigger a series of catastrophic events,leading to cytosolic Ca2+overload-driven cell death.[2–4]

Because of the delicate role of Ca2+in both cell survival and death, IP3R-mediated Ca2+release must be carefully balanced.[5]This release is exquisitely modulated by Ca2+itself,[6]or by an expanding group of messengers, such as IP3,[7]cytochrome c,[8]and Bcl-2 (B-cell lymphoma-2).In addition to its well-known pro-survival role by counteracting mitochondrial outer membrane permeabilization at the mitochondria,[9]Bcl-2 also prevents cell death by preventing excessive IP3R-mediated Ca2+elevation at the ER.[10,11]Recent experimental studies revealed that Bcl-2 can suppress IP3R-mediated Ca2+release from the ER via two distinct mechanisms. On the one hand, Bcl-2 via its BH4 domain directly binds to the regulatory and coupling region of IP3R,preventing IP3R-mediated Ca2+release,thereby inhibiting Ca2+induced cell death.[12–15]On the other hand, Bcl-2 serves as a docking platform for both calcineurin(CaN)and dopamineand cAMP-regulated phosphoprotein of 32 kDa(DARPP-32),createing a negative feedback loop that regulates IP3R phosphorylation and thus indirectly prevents Ca2+elevation that induces cell death.[16]We term the first one “direct mechanism”,and the second one“indirect mechanism”.

Despite these experimental results, the global dynamic behaviors of Bcl-2 inhibition in IP3R-mediated Ca2+signaling are not completely understood due to the complex interactions among the components that involved in the direct or indirect mechanism. In particular,it remains unexplored how they jointly affect Ca2+signal and which mechanism is more potent in the suppression of Ca2+release.

Although the dynamic mechanisms underlying cellular signaling seem overwhelmingly complex, they can be clearly understood by the mathematical modeling using ordinary differential equations (ODEs) based on biochemical kinetics.[3,17–20]Recently,we have constructed a model to systematically study the signaling pathway of Ca2+release regulated by Bcl-2 indirectly,[21]which can be called the indirect mechanism model. In the current study, we develop a direct mechanism model and integrate it into the indirect mechanism model. We employ these two mechanism models, separately and in combination, to further dissect the inhibitory effect of Bcl-2 on Ca2+signal theoretically. In particular, we demonstrate that the indirect mechanism is more potent than the direct mechanism in preventing Ca2+release from the ER and that the two mechanisms dampen Ca2+signal synergistically.Since Bcl-2 suppression in Ca2+release is exploited by cancer cells to escape cell death,the present study may shed light on future therapeutic approaches for the treatment of cancer.

2. Model

As the model is complex, we shall describe it in the following steps:

(1)A general Ca2+oscillation model.

(2)The details of the direct mechanism model(Fig.1(a)).

(3) The details of the indirect mechanism model(Fig.1(b)).

(4)How the two models are incorporated together into a dualmechanism model(Fig.1(c)).

(5)How to determine the model parameters.

Fig.1. (a)Kinetic schemes of the direct mechanism model. For simplify,it is assumed that all IP3Rs are phosphorylated(pIP3R).Left: Each subunit of pIP3R has one IP3 binding site,two Ca2+ binding sites,and one Bcl-2 binding site. These sites can be occupied(represented by 1)or empty(represented by 0),and thus there are sixteen possible states(see from the top view). Right:The kinetics on the top and bottom faces of the inner and outer cubes as well as the kinetics between the two cubes. (b)Schematic diagram of the indirect mechanism model. The reversible conversion between phosphorylated and non-phosphorylated forms of IP3R is catalyzed by PKA and PP1. IP3 binds to IP3R/pIP3R and modulates Ca2+ release. The release of Ca2+ from pIP3R is stronger than that from IP3R.An increase in Ca2+ level leads to activation of CaN,which dephosphorylates pDARPP-32 into DARPP-32. During this process,Bcl-2 serves as a platform docking CaN and pDARPP-32. PKA catalyzes DARPP-32 into pDARPP-32, which is an inhibitor of PP1. (c)Mechanism of the coupled model.The direct and indirect mechanisms are linked by Bcl-2 regulation of flux through Ca2+ channel, i.e., IP3R and pIP3R.The direct mechanism influences the channel open probability by determining the fraction of channel subunits in state S1100,while the indirect mechanism influences the maximal channel flux by determining the IP3R-to-pIP3R ratio.

2.1. Ca2+oscillation model

For a closed cell, Ca2+oscillations mainly derive from three types of fluxes between the ER and the cytosol: IP3R channel-mediated Ca2+release from the ER into the cytosol(JChan),Ca2+leakage from the ER into the cytosol(JLeak),and SERCA-dependent Ca2+uptake from the cytosol into the ER(JSERCA).

The driving force for Ca2+flow from the ER to the cytoplasm is the concentration difference between them. We get

Here,Pois the open probability of the IP3R channel,u1is the maximal Ca2+channel flux, andu2is the Ca2+leak flux constant. ER Ca2+concentration([Ca2+]ER)is determined by conservation conditionc0=c1[Ca2+]ER+[Ca2+].

The SERCA-dependent Ca2+pump is described by a Hill equation,with a Hill coefficient of 2,

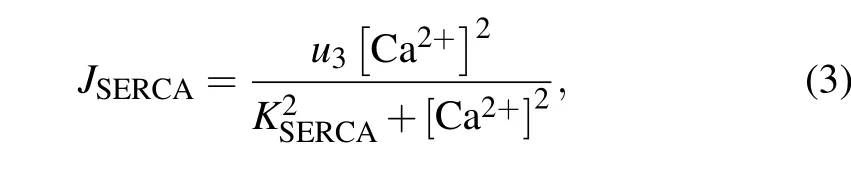
whereu3is the maximal uptake flux of Ca2+, andKSERCAis the activation constant for SERCA.

2.2. Direct mechanism model

In construction, the direct mechanism model is based on De Young–Keizer model. De Young and Keizer assumed that three equivalent and independent subunits are involved in the opening of an IP3R,each subunit of which has one IP3binding site,one activating Ca2+binding site,and one inhibiting Ca2+binding site.[22]According to the experimental results,[12–15]Bcl-2 directly binds to the IP3R, so we can assume that each subunit has one Bcl-2 binding site. Thus,each subunit of IP3R may exist in sixteen states with transitions governed by binding rates(ai)and unbinding rates(bi). The state of each subunit is denoted asSijkn, where the indexirepresents the IP3binding site,jthe activating Ca2+binding site,kthe inhibiting Ca2+binding site,andnthe Bcl-2 binding site. An occupied site is represented by 1, and an empty site by 0. The fraction of subunits in stateSi jknis denoted byxi jkn.

According to the law of mass action, the ODEs describing the dynamics of a subunit can be written down. Due to the space limitation,only the ODE forx1100is presented in the main text,

and the other fifteen ODEs are given in the supplementary material.

Similar to the consideration of De Young–Keizer model,[22]we further assume that a subunit is active only when IP3and activating Ca2+sites are occupied but inhibiting Ca2+and Bcl-2 sites are unoccupied (S1100) and that all three subunits must be in this state for the IP3R channel to be open.With these assumptions,Pois written as

2.3. Indirect mechanism model

The IP3R(herein refers to type-1 IP3R,whose amino acid at position 1755 is serine) has two forms: phosphorylated(pIP3R)and non-phosphorylated(IP3R),and phosphorylation results in enhanced Ca2+release.[23]If we letkdenote the maximal Ca2+release rate per micromole of IP3R, and letαdenote the release rate ratio of pIP3R to IP3R(1<α ≤9),u1mentioned above can be modified as

As done in our previous work,we setα=6,because we have demonstrated that the value ofαwill not significantly affect our result.[21]

The transition between the two forms of IP3R is catalyzed by two enzymes: protein kinase A (PKA) which phosphorylates IP3R at Ser1755 into pIP3R and protein phosphatase 1 (PP1) which dephosphorylates pIP3R into IP3R.[24]Phosphorylation and dephosphorylation rates are often modeled by Michaelis–Menten equation,[25]thus,

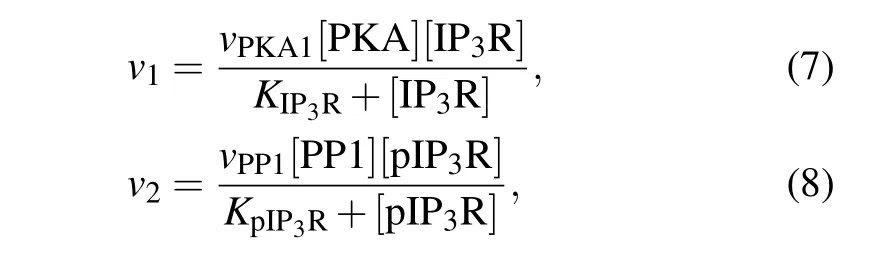
wherevPKA1andvPP1are the maximal reaction rate,andKIP3RandKpIP3Rare the Michaelis constants.

CaN is a Ca2+-activated protein phosphatase that has four Ca2+binding sites. Ca2+binding sites 1 and 2 are of lower affinity withKds (dissociation constants) in the micromolar range,whereas Ca2+binding sites 3 and 4 are of higher affinity withKds in the nanomolar range.[26]So we only consider the first two binding sites, and the evolution for active CaN(CaN∗)is assumed to be given by mass-action kinetics

Bcl-2 serves as a platform, in which CaN∗dephosphorylates the phosphorylated DARPP-32(pDARPP-32)into DARPP-32.[16]The corresponding reaction rate is

2.4. Dual-mechanism model

The nexus between the direct mechanism and the indirect mechanism primarily lies in the Bcl-2 regulation of IP3R channel, i.e., the termJchanin Eq.(1). The direct mechanism influencesPoby determiningx1100, while the indirect mechanism influencesu1by determining the ratio between IP3R and pIP3R. In addition, we assume that for a certain Bcl-2 molecule,it can only participate in either one of the two mechanisms. If we let the proportion of Bcl-2 involved in the direct mechanism beβ,then the one involved in the indirect mechanism is 1−β.

The ODEs which describe the dynamical process of all species (except the sixteen states of IP3R/pIP3R) involved in the Bcl-2 regulation of Ca2+signaling are

2.5. Model parameters

The specific meaning of each parameter in the De Young–Keizer model can be found in Ref. [22]. Under its default parameters, the peak value of Ca2+oscillations is 0.16–0.47 µM, and the period is 11.4–15.6 s. Due to the need to fit the peak value and period of the Ca2+oscillations in the experiments,[12,16]the values of some relevant parameters in the original model must be rescaled. The parameters in the De Young–Keizer model,together with the binding and unbinding rates of Bcl-2 and IP3R,constitute the parameters of the direct model(see Table S1).Table S2 lists the parameters of the indirect model,among which the protein concentrations are drawn from Refs.[27–30],reaction ratesk1andk2are obtained from Ref.[29],and the remaining reaction rates are adjusted by fitting the experimental results in Ref.[16].[IP3]and[Bcl-2]are the two independent input variables,and[Ca2+]is the output variable.

3. Results

Although both the direct mechanism and indirect mechanism of the Bcl-2 regulation of Ca2+signaling can be present simultaneously, it is better to first capture their respective roles. After separately evaluating the respective roles of the direct mechanism and indirect mechanism, we then examine the comprehensive effects of the dual mechanisms.

3.1. Time course of Ca2+signaling

As for the direct mechanism model, all IP3Rs are postulated to be in the phosphorylated form. We do not consider the dephosphorylated form based on the following two considerations. On the one hand, to our best knowledge, there is no reference available for measuring the ratio of phosphorylated to dephosphorylated IP3R.Nonetheless,it is clearly that the pIP3R is the dominant form for releasing Ca2+.[23]On the other hand,the concurrent consideration of the two forms will make each IP3R subunit have a phosphorylation binding site,and there will be five binding sites in total, which will make the modelling very complex.Moreover,the results obtained by the opposite postulate (Fig. S1) reveal that it only has a limited impact on the conclusion.The time-course plots show that when[Bcl-2]=0.15µM the peak value of Ca2+oscillations is more than 0.28µM(Fig.2(a)),while when[Bcl-2]=0.3µM the peak value is about 0.17µM(Fig.2(b)).

As for the indirect mechanism model,an IP3R exists in either phosphorylated or unphosphorylated form, the transition of which is regulated by PKA and PP1. The time-course plots show that when[Bcl-2]=0.15µM the peak value of Ca2+oscillations is more than 0.34µM(Fig.2(c)),while when[Bcl-2]=0.3µM the peak value is about 0.12µM(Fig.2(d)).

Although the results of Fig. 2 indicate that Bcl-2 seems to have an effect on the frequency of Ca2+oscillations, the two core references[12,16]underlying our modeling work do not mention the impact of Bcl-2 on the frequency. Furthermore, we have recently demonstrated that it is the amplitude,but not the frequency of Ca2+oscillations that regulates apoptosis induction.[3]Hence,we hereafter only focus on the effect of Bcl-2 on the amplitude of Ca2+oscillations.

Taken together,both the direct mechanism model and the indirect mechanism model indicate that Bcl-2 has an inhibitory effect on Ca2+oscillations,and the simulation results are qualitatively consistent with the observations.[12,16]

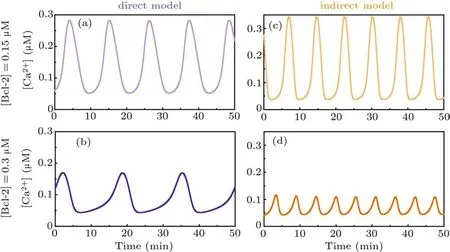
Fig. 2. Time course of Ca2+ signal for direct mechanism model when [Bcl-2] is 0.15 µM (a) and 0.3 µM (b), respectively. Time course of Ca2+ signal for indirect mechanism model when[Bcl-2]is 0.15µM(c)and 0.3µM(d),respectively.

3.2. One-parameter bifurcation analysis

Next we use one-parameter bifurcation diagram to character the influence of Bcl-2 on Ca2+signal from a global point of view. The Hopf bifurcation diagrams in Fig.3 illustrate that when [Bcl-2] is used as a control parameter, a stable steady state loses stability and gives birth to limit-cycle oscillations,which are born at the Hopf bifurcation point (abbreviated as BP).

The similarities between the direct mechanism model and the indirect mechanism model are: (1) for [Bcl-2]< BP1,there is one stable steady state corresponding to higher[Ca2+];(2) for [Bcl-2]> BP2, there is one stable steady state corresponding to lower [Ca2+]; (3) for BP1< [Bcl-2]< BP2,the amplitude of Ca2+oscillations first increases and then decreases when[Bcl-2]increases,but in a broad parameter range it decreases with increasing[Bcl-2]. The major distinction between them is that the BP1 of the direct mechanism model is a supercritical Hopf bifurcation point(Fig.3(a)),while the BP1 of the indirect mechanism model is a subcritical Hopf bifurcation point(Fig.3(b)). The difference between the supercritical and subcritical Hopf bifurcation points is that a stable limit cycle with small amplitude appears at the former,whereas at the latter an unstable limit cycle occurs, the amplitude of which grows quickly until it connects with the large amplitude, stable limit cycle.[31]

Collectively, the one-parameter bifurcation analysis for the direct mechanism model and the indirect mechanism model suggests that Bcl-2 can inhibit Ca2+release from the ER.

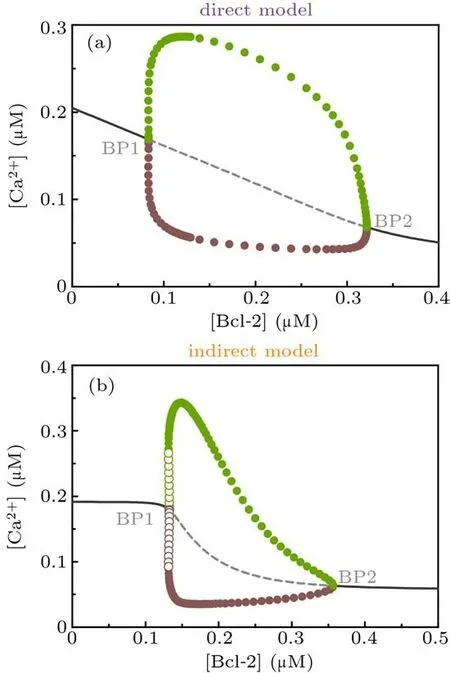
Fig. 3. One-parameter bifurcation diagrams of [Ca2+] against [Bcl-2] for direct mechanism model (a) and indirect mechanism model(b). Solid/dashed line: stable/unstable steady state; filled/empty circle: maximal (green) and minimal (brown) values attained by a stable/unstable limit cycle oscillation. BP,bifurcation point.

3.3. Two-parameter bifurcation analysis

The above results are obtained under the condition of a fixed [IP3]. We next employ two-parameter bifurcation analysis to further assess the effects of simultaneous inputs,i.e.,a varied combination of[IP3]and[Bcl-2],on Ca2+oscillations.

In the two-parameter bifurcation diagrams (Fig. 4), stable limit-cycle oscillations only occur within the color regions,which correspond to the appropriate parameter combinations of [IP3] and [Bcl-2]. Here, we focus on the peak value of Ca2+oscillations because excessive Ca2+elevation triggers cell death.[3,16]Figure 4(a) displays that for the direct mechanism model, although Bcl-2 may elevate the peak value in a narrow parameter interval at the left border, it represses the peak value in a broad parameter space. For the indirect mechanism model (Fig. 4(b)), the peak value of Ca2+oscillations caused by a fixed [IP3] for a higher [Bcl-2] is always significantly smaller than the one for a lower[Bcl-2],suggesting that Bcl-2 suppresses the peak value.

In both the direct mechanism model and the indirect mechanism model, as[Bcl-2]increases, it first passes a Hopf bifurcation point (e.g., BP1 in Fig. 3), where Ca2+oscillations appear with small amplitude and grow larger as[Bcl-2]is increased further. In the indirect mechanism model,the bifurcation point is a supercritical Hopf bifurcation point,where stable Ca2+oscillations with large amplitude appear abruptly.These are the mathematical foundations underlying the appearance at the left boundary of the oscillation region.

In summary, the two-parameter bifurcation analysis for the direct mechanism model and the indirect mechanism model demonstrates that Bcl-2 can restrain exaggerated Ca2+release.

3.4. Mathematical analysis

All the above findings indicate that the indirect mechanism seems to be more effective in suppressing Ca2+signal than the direct mechanism. Specifically, the indirect mechanism not only suppresses the oscillation amplitude(especially the peak value)in a larger range,but also suppresses the peak value more potently. In the following, we use mathematical analysis to quantify their efficiency in repressing Ca2+flux from Ca2+channel,i.e.,IP3R and pIP3R.

In the direct mechanism,the Ca2+channel is occupied by Bcl-2, which pulls it away from the open state. The channel open probability can be calculated by the deterministic matrix transition method.[32,33]When the system is in equilibrium,xi jkncan be expressed byx0000,for example,

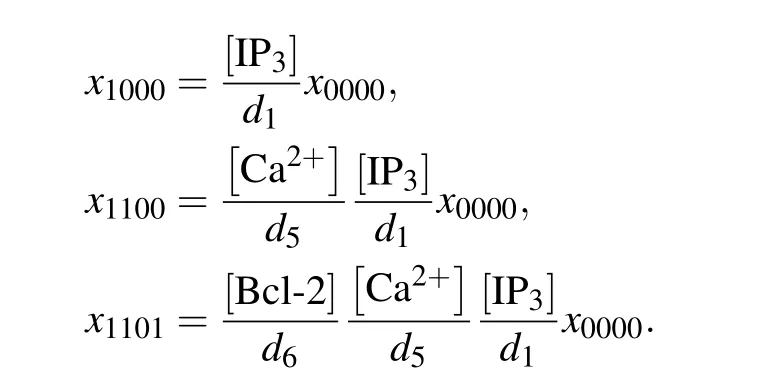
Then the normalized equilibrium probability for state(ijkn)is

Therefore,the normalized equilibrium probability for the open state is

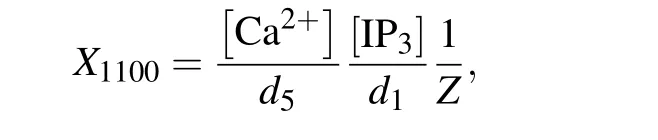
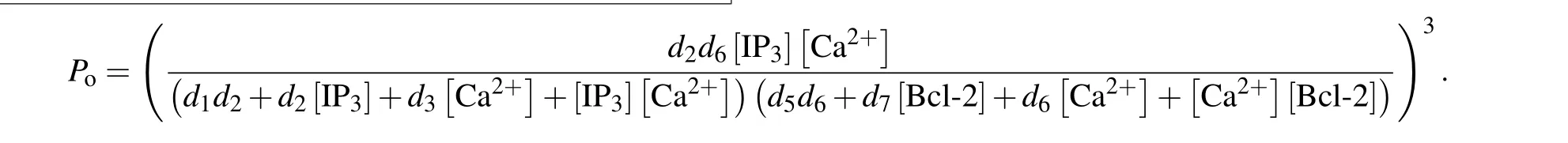
and thus the channel open probability is Here,diis the dissociation constant for each binding site.And according to the detailed balance principle,d7=d5d6/d8.Consequently,Pois a function of [IP3], [Ca2+], and [Bcl-2].From Fig.5(a)we can see that with fixed[IP3]and[Ca2+],Popresents a progressive decreasing trend with increasing [Bcl-2].

In the indirect mechanism,Bcl-2 regulates the conversion of pDARPP-32 to DARPP-32, which indirectly controls the ratio between IP3R and pIP3R,and thereby the maximal Ca2+channel flux.Considering that system(16)is in steady state for[Ca2+]=0.2 µM, we obtain the expression of [pDARPP-32]by solving the equationv3−v4=0,and then insert it intov2.Then we derive the expression of IP3R by solvingv1−v2=0.By substituting IP3R into formula(6),we can give the expression of the maximal Ca2+channel flux with respect to[Bcl-2]([Bcl-2]is denoted asBfor convenience),

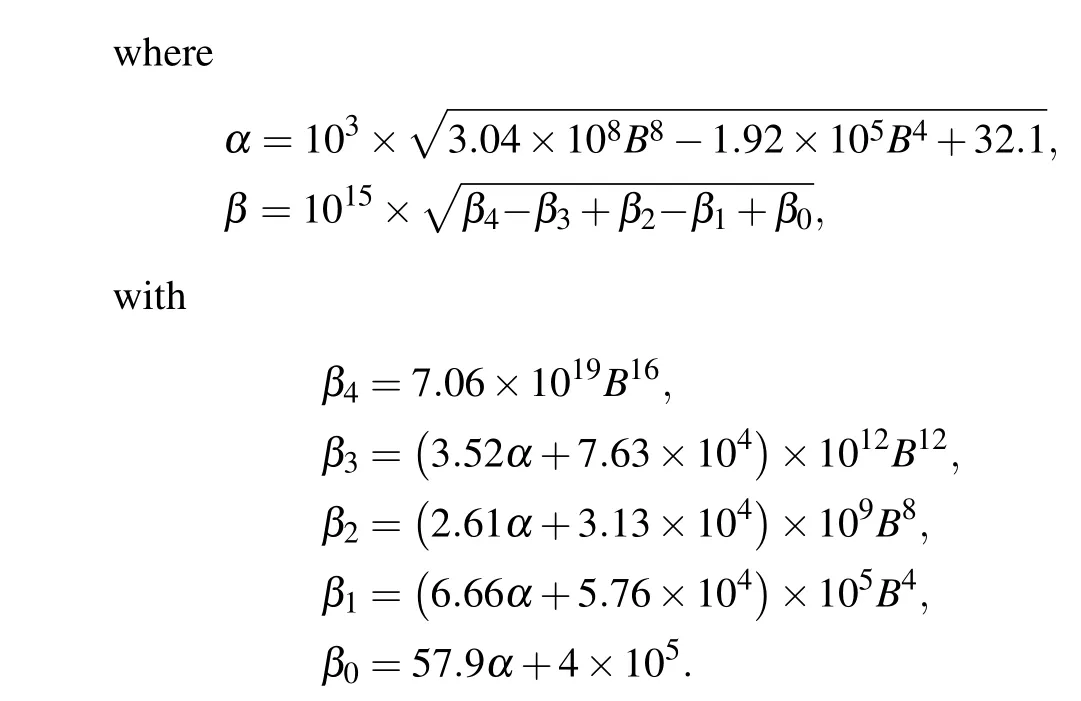
As shown in Fig.5(b),u1shows an ultrasensitive response to[Bcl-2],i.e.,small increases in the level of Bcl-2 lead to large decreases in the maximal Ca2+channel flux within the physiological range of Bcl-2(0.05µM to 0.65µM,[34]highlighted in green).

One may think that the sharp relationship between the maximal Ca2+channel flux and [Bcl-2] is ascribed to that the Hill coefficient in Eq. (13), which reflects the regulation strength of Bcl-2 on the conversion of pDARPP-32 into DARPP-32, is equal to 4. In fact, the lower Hill coefficient,such as 1,yields the same qualitative result(Fig.S2).

Using mathematical analysis, we confirm the inhibitory effect of Bcl-2 on Ca2+release,and further prove that the indirect mechanism is more efficient than the direct mechanism,especially in the physiological concentration range of Bcl-2.

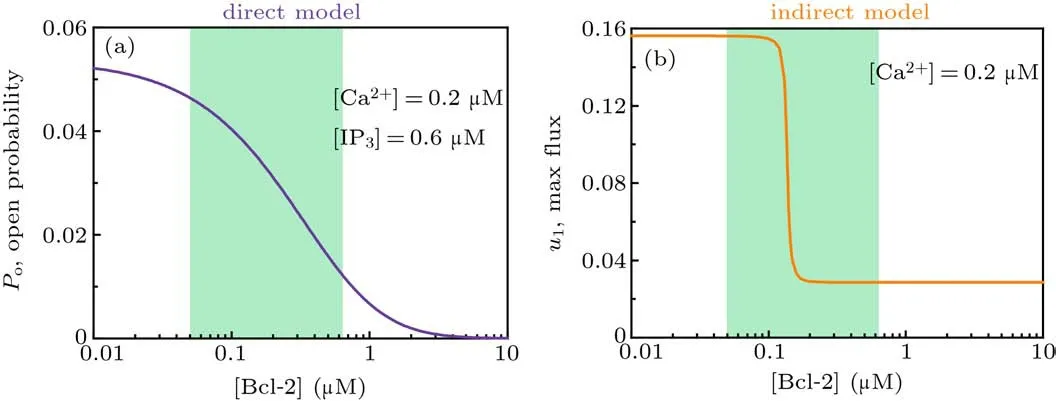
Fig. 5. Mathematical analysis results. (a) For the direct mechanism model, the channel open probability is plotted versus [Bcl-2] when[IP3]=0.6µM and[Ca2+]=0.2µM. (b) For the indirect mechanism model, the maximal Ca2+ channel flux is plotted versus[Bcl-2] when[Ca2+]=0.2µM.The physiological range of Bcl-2 is highlighted in green.

3.5. Dual-mechanism model analysis

Given the different efficiency of the direct and indirect mechanisms on Ca2+release,we lastly examine their combination effect on Ca2+signal. For a fixed amount of Bcl-2,it is unclear how many Bcl-2 are involved in the direct or indirect mechanism. As mentioned above, we useβ(1−β) to represent the percentage of Bcl-2 involved in the direct(indirect)mechanism

Figure 6 shows the one-parameter bifurcation diagrams of [Ca2+] against [Bcl-2] for different combinations of the direct and indirect mechanisms. Compared with Fig. 3, we can see that whenβ=0.5,the one-parameter bifurcation diagram looks like a hybrid of the direct and indirect mechanisms(Fig.6(b));whenβ=0.8,it looks more like the one of the direct mechanism(Fig.6(a)); whenβ=0.2, it looks more like the one of the indirect mechanism(Fig.6(c)). In addition,the parameter range of[Bcl-2]that causes Ca2+oscillations in the dual-mechanism model seems to be wider than the one in either single mechanism.

Fig. 6. One-parameter bifurcation diagrams of [Ca2+] against [Bcl-2] for dual-mechanism model under different combination of direct and indirect mechanisms,i.e.,β =0.8(a),β =0.5(b),and β =0.2(c). The graphical notations are similar to those in Fig.3.

Generally, when two factors act together, their combination effect can be classified into three main types: additive,if the combination effect is equal to the sum of the effect of individual factors; synergistic, if the combination effect is higher than additive; and antagonistic, if the combination effect is lower than additive.[35]

As the dual-mechanism expands the range of Bcl-2 that triggers Ca2+oscillations,the direct and indirect mechanisms act synergistically.

4. Discussion

As a critical modulator of IP3R,[36]Bcl-2 prevents Ca2+release from the ER either by directly binding the IP3R[12]or by indirectly decreasing IP3R phosphorylation through a negative feedback loop.[16]The apparent complexity of the two mechanisms is further increased by their intertwined relationship with each other.Furthermore,a research connecting these two mechanisms is still lacking. By developing mathematical models for the direct and indirect mechanisms and then combining them into a dual-mechanism model, we provide a holistic view of how Bcl-2 represses Ca2+release from the ER theoretically.

The major findings of the present study are that (1) although Bcl-2 acts differentially in the direct and indirect mechanisms, its inhibitory effect on Ca2+signal is similar in both mechanisms; (2) the indirect mechanism is more potent than the direct mechanism in inhibiting Ca2+signal;and(3)the direct and indirect mechanisms suppress Ca2+signal in a synergistic manner,which may expand the richness in the message conveyed by Bcl-2.

Since it is still challenging to determine how much the inhibitory effect of Bcl-2 on Ca2+signal results from purely the direct mechanism and how much from the indirect mechanism, the second and third findings ought to be assessedin vivoand the full complexity of the relationship between the two mechanisms ought to be further characterized in more detail. Nevertheless,our work can be viewed as a starting point to uncover their complex relationship.

An appropriate elevation of Ca2+is critical for cell survival,while high amplitude Ca2+elevation triggers cell death including apoptosis. Bcl-2, directly or indirectly, regulates IP3R,thereby dampening its proapoptotic Ca2+-release properties and promoting the survival of cancer cells.[37,38]This may allow for exquisite control of Bcl-2’s inhibitory property on Ca2+signal and thus be important for cancer treatment by modulating the direct and indirect mechanisms together.Given that some Bcl-2 inhibitors have progressed into clinical studies,[39,40]the two complementing mechanisms need to be quantitatively considered in order to develop precision medicines that target cancers.

Overall, this study provides a theoretical understanding for the direct and indirect mechanisms of Bcl-2 suppression in Ca2+release,which might be important in terms of efforts to target Bcl-2 for cancer treatment to achieve optimal effect. In addition, our findings may be useful to understand how other members of the Bcl-2 protein family,including Bcl-xL[41]and BOK,[42]modulate Ca2+release from the ER.