基于马尔可夫链理论的埋地钢管内腐蚀状态预测分析

陈 伟 王友义 严俊伟 陈 长

（1.浙江省特种设备科学研究院；2.浙江省特种设备安全检测技术研究重点实验室）

管道输送是油气工程和市政工程中流体介质最主要的运输方式。 城市市政管道和油气管道可在地下延伸数百公里， 由于地质条件复杂，地下管网易受外部环境的损伤，其中管道腐蚀是最常见、最重要的损伤模式。 我国华东地区经济发达，频繁的市政建设工程可能使地下管道受到严重的第三方破坏，如外保护层破损、阴保失效等。公开发表的文献中研究管道腐蚀的方法主要包括模糊逻辑理论、阿伦尼乌斯外推法、灰度理论及蒙特卡洛-马尔可夫理论等。Mohsin K M等基于模糊逻辑理论建立了一种预测保温层下管道腐蚀状态的模型，该模型考虑了影响管道腐蚀状态最关键的5种因素（保温层状态、保温层类型、环境因素、管道复杂程度和运行温度），预测结果显示，保温层类型对管道腐蚀状态影响最显著［1］。胡松青等基于BP神经网络理论分析得知影响输油管道内腐蚀速率的主要因素为介质硫含量和酸值［2］。 Wang H等基于隐藏马尔可夫理论建立了一种群论方法来预测埋地管道外腐蚀状态的变化规律，通过对某110 km管道的分析可知，结合该理论与土壤分析、管道内检测等手段可更精确分析管道整体腐蚀状态的变化［3，4］。 Ossai C I等通过蒙特卡洛-马尔可夫理论分析了内腐蚀管道的可靠性并将该理论用于分析某X52钢管［5，6］。

笔者基于离散马尔可夫链理论建立了管道内腐蚀状态预测模型，通过漏磁内检测器和超声测厚手段获取了浙江省内某管道的3个检验周期内壁厚数据并代入预测模型。

1 管道内腐蚀的离散马尔可夫模型

检验周期中管道的腐蚀时间和腐蚀量皆可当成离散空间变量，即管道的腐蚀过程具有马尔可夫性。 笔者假设马尔可夫过程（{Xn，n∈T}）中的参数T（T=1，2，3，…，n）属于离散时间变量且Xn属于离散空间集S={i0，i1，i2，i3，…，in}，如果参数n和状态集合（i0，i1，i2，i3∈S）满足如下条件［7］：

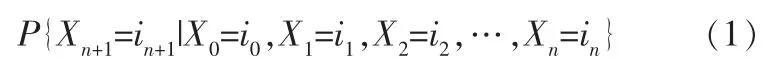
则该马尔可夫过程{Xn，n∈T}可当成马尔可夫链，且条件概率方程pn（i，j）=P｛Xn+1=j｜Xn=i｝称为从状态i到状态j的一步转移概率。 其一步转移概率矩阵为［8］：

对于马尔可夫链，其一步转移概率矩阵具有如下性质：

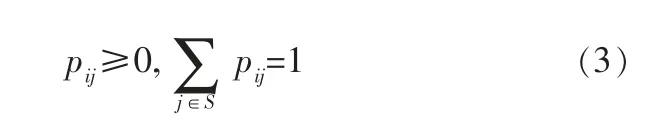
其中，pij=P{Xm+n=j│Xm=i}是条件转移概率，P（n）=是马尔可夫链的n步转移概率矩阵，具有如下性质：

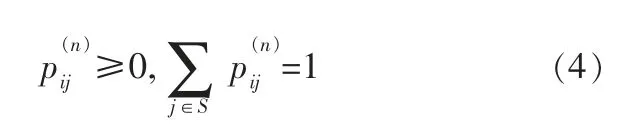
当n≥0且0≤l≤n时，该矩阵具有如下性质：

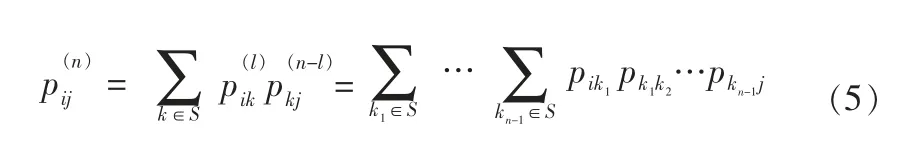
式（5）揭示了n步转移概率矩阵可由一步转移概率矩阵定义，将埋地管道腐蚀过程定义为马尔可夫过程，则转移概率仅与检验时的腐蚀状态有关而与检验时间无关，其初始状态空间为［9］：

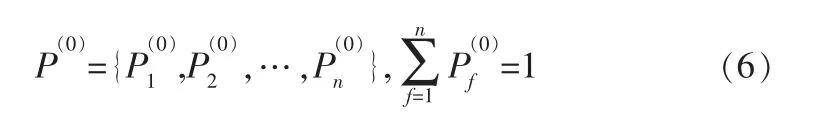
结合实际情形，如果管道的初始状态p（0）是已知的，则其第n步状态为：

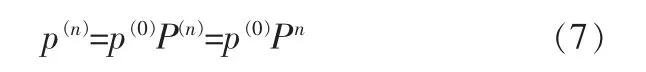
2 管道腐蚀状态评估流程

通过马尔可夫链评价管道的腐蚀状态主要包括3个步骤［10］：确定管道腐蚀状态的壁厚标准；确定管道腐蚀初始状态并建立腐蚀状态转移概率矩阵；确定管道腐蚀过程属于马尔可夫过程并预测其腐蚀状态变化。

2.1 管道腐蚀状态的壁厚标准

CJJ95—2013《城镇燃气埋地钢质管道腐蚀控制技术规程》依据管道剩余壁厚要求或剩余强度要求将管道腐蚀状态划分为7个等级［11］（表1）。 其中Tmin（最小安全壁厚）可通过ASME B31G 获得［12］。 为了方便评价管道腐蚀状态，将表1中7种腐蚀状态等级简化为5种等级（Ⅰ——轻微腐蚀，Ⅱ——中度腐蚀，Ⅲ——严重腐蚀，Ⅳ——非常严重腐蚀，Ⅴ——失效），对应的，在马尔可夫链中其状态向量可表述为K=［1，2，3，4，5］。

表1 管道腐蚀损伤评价指标

2.2 状态转移概率矩阵

当管道腐蚀状态已确定，可建立相应的状态转移概率矩阵。 该矩阵中每个元素皆代表管道状态处于从“轻微腐蚀”到“失效”的5种状态中的某一种状态，典型的状态转移概率矩阵如下［13］:

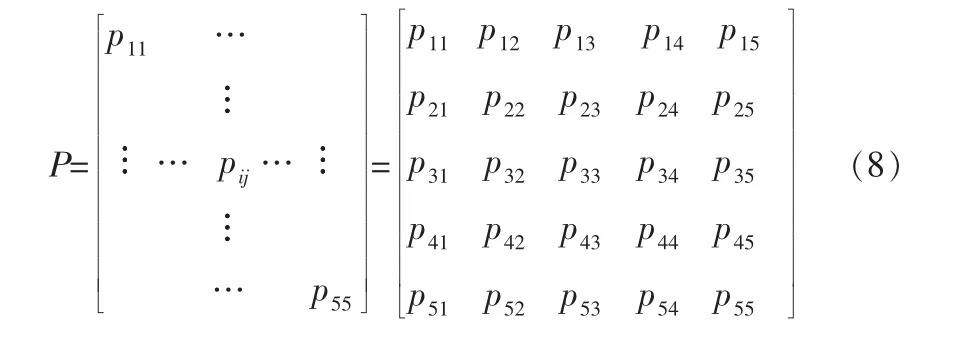
式（8）中的矩阵元素pij代表管道腐蚀状态从状态i一步转移到状态j的概率，实际情形中由于管壁的腐蚀状态是不可逆转的， 不采取补救措施的情形下管道的腐蚀状态只能更加恶化而不可能逆转［14］，即当i＞j时，pij=0，因此可将式（8）简化为：

3 实例分析

选取宁波市至衢州市的管网中某段管道作为分析对象，该段管道长167 km，管道尺寸规格φ406 mm×8 mm。 管道腐蚀状态具有随机性，此处选取蚀坑深度最大的位置作为评价对象。 管道服役后第15年进行了第1次基于漏磁技术的内检测，检测器示意图如图1所示。

图1 基于漏磁技术的管道内检测器

检测器性能参数如下：

净长度 4 542 mm

净重 515 kg

最大运行速度 5.5 m/s

最小运行速度 0.3 m/s

检测里程 167 km

运行时间 34 h

运行压力 1.5 MPa

运行温度 0～40 ℃

为了方便内检测时的收球和发球操作，对管道结构进行改造，增加了收球筒和发球筒的长度并加大端盖打开角度。 此次检测发现管道最大腐蚀深度为4 mm。 由于最大腐蚀深度已大于50%管道原始壁厚，因此下次检验周期缩短为3年（管道服役后第18年）。

第2次检验基于超声测厚原理， 重点关注前一次检验中发现的壁厚最薄的位置。 此次检验中测得管道最大腐蚀深度为4.8 mm。

第3次检验为管道服役后第20年， 基于超声测厚原理本次检验测得同一位置管壁最大腐蚀深度为5.0 mm，测试现场如图2所示。

图2 剥离防腐层后管道本体

简化后管道腐蚀状态评价标准见表2。

表2 简化后管道腐蚀状态评价标准

最后一次检验时测得的管道最大腐蚀深度为5.0 mm，管道剩余壁厚3.0 mm，由表2可知此时管道腐蚀状态为4（非常严重腐蚀），对应腐蚀状态向量K=［0，0，0，1，0］。一般而言，都认为在外界环境保持基本不变的情形下，管道剩余壁厚随时间的变化规律符合指数规律，其经验公式为［15，16］：

式中 a、h——非量纲因子；

t——使用年限，a；

δ——管道剩余壁厚，mm。

将4组检验数据（包括t=0，δ=8）代入式（10）并采用最小二乘法进行曲线拟合，可确定式（10）中未知参数：

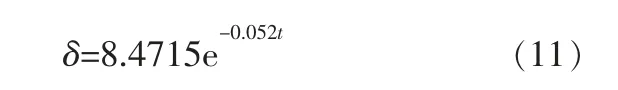
对式（11）中t分别赋值1，2，3，4，5…可确定对应年限的剩余壁厚δ。 结合管道腐蚀状态评价标准，可获得不同时期管道腐蚀等级（表3）。

表3显示了管道腐蚀等级随使用年限的变化规律，为了使腐蚀等级变化趋势更明显，可分别求出不同时期管道最大概率状态。 文中管道腐蚀状态为离散时间序列，不同时期管道腐蚀等级的转移概率矩阵可通过如下所述统计方法获得。

定义gi为状态i出现的次数，gij为从状态i一步转移到状态j的次数，pij为从状态i到状态j的一步转移概率，则可得：

根据表3中所列的腐蚀等级可获得管道腐蚀状态的一步转移概率矩阵：

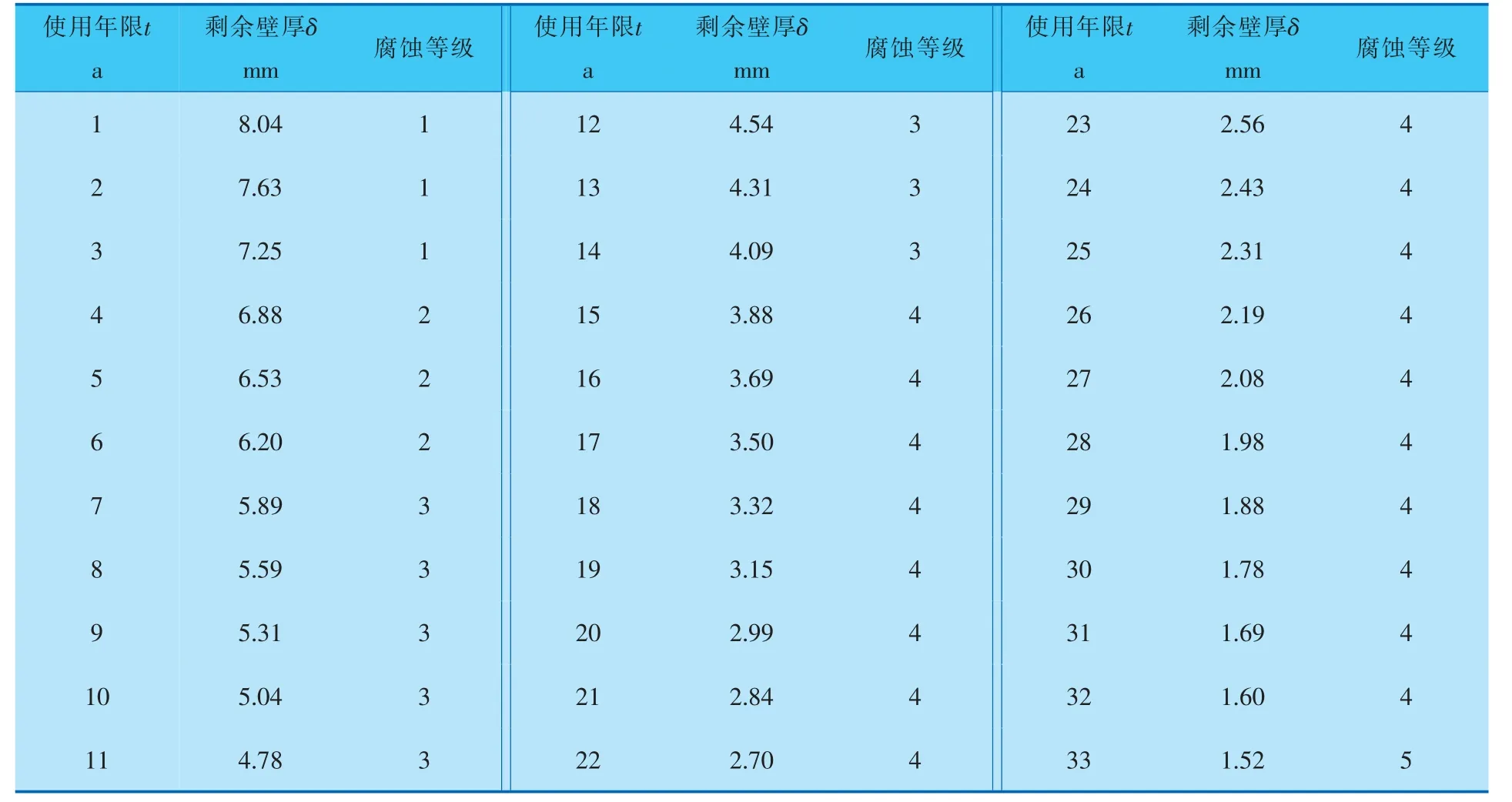
表3 不同时期管道腐蚀等级

此处选取最后一次（第20年）检验数据作为初始条件，代入到马尔可夫链中预测管道腐蚀状态的变化规律。 结合式（4）、（13），可得管道腐蚀状态预测结果见表4。

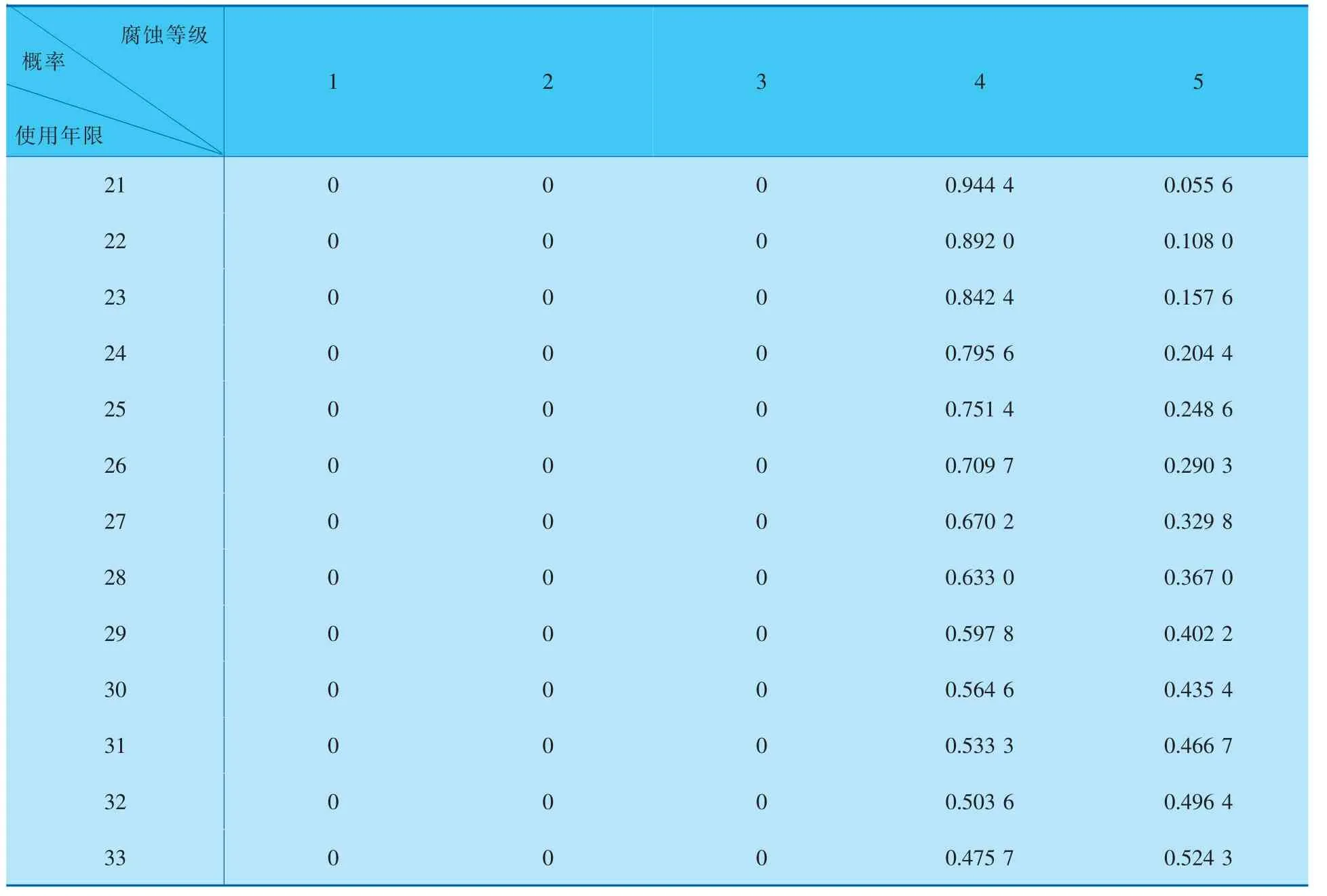
表4 管壁腐蚀等级预测结果

由表4中预测结果可知， 该段管道将在服役33年后失效，该结果与表3中的预测结果相吻合，说明数据量有限的情形下，仍可通过马尔可夫链理论预测管道的腐蚀状态变化趋势。 但是该预测结果与“初始状态”的选取有关，通过计算可知当选取第18年的检验数据作为“初始状态”时，通过马尔可夫理论预测的管道失效时间为服役后第31年。 若忽略二者之间微小的差距，则采用马尔可夫链理论预测管道腐蚀状态变化趋势的优势仍不可忽略。

由于相邻两次检验周期之间时间间隔长达数年且现场的工作环境恶劣，同时不同检验周期中的检验工作可能由不同检验单位承担，导致获得同一缺陷的连续多次检验数据的可操作性较低。 因此目前已公开发表的文献中涉及到的管道检验数据大都为3个或3个以下检验周期内获得的数据。 对于非连续时间周期内的检验数据，一种可行的方法是将灰度理论引入马尔可夫链［17］。总体而言，灰度理论是对原始数列进行重新生成操作以使新数列满足某种已知的分布模型。 例如对于广泛应用的灰度理论模型GM（1，1），重新生成操作是对原始数列进行一次累加操作（1-AGO）［18］，即：

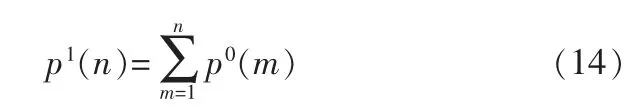
其中，p0（m）为原始数列，p1（n）是新生成的1-AGO数列，此步操作可将任何非负、非摆动数列转化为递增数列［19］。 有关灰度理论在非连续检验数据中的应用在接下来的研究重点之一。

4 结束语

笔者基于马尔可夫链理论分析了埋地腐蚀状态的变化趋势， 结合CJJ95—2013 与ASME B31G确定了以管壁剩余厚度为依据来划分管道腐蚀状态。 以某段管道中3组腐蚀数据为例，采用本模型分析了该段管道的腐蚀状态变化规律。 分析结果显示，该段管道将在服役33年后因腐蚀失效，尽管该预测结果受预测模型中管道“初始状态”选取的影响，但仍能反映出该管道的腐蚀状态随时间的变化趋势。 对于非连续的检验数据，亦初步探讨了引进灰度理论对数据进行处理的可行性，所提出的预测方法和管道腐蚀状态划分标准对埋地管道的检验工作具有一定指导意义。