快速启闭阀阻尼腔特性分析与结构优化
2021-10-28陈修高夏志明张希恒
赵 佳 陈修高 周 义 夏志明 张希恒
(1.兰州理工大学石油化工学院;2.国家电投集团科学技术研究院有限公司;3.博雷控制系统有限公司)
冲击是在工程领域中经常遇到的力学现象[1],在阀门的开启过程中也不可避免。 快速启闭阀由于工作环境特殊[2],公称通径大,阻尼腔空间小、行程短,阀芯重且动作速度快,在快速运动至行程终端时,往往会发生剧烈的冲击和振动,使系统工作不稳定, 甚至出现密封件失效的情况,影响阀门使用寿命, 因此在其行程终端设置阻尼腔, 以防止和减少活塞在运动时对阀体的冲击,在一定程度上能起到阻尼的作用[3]。 但在实际工作过程中,由于阻尼腔泄压孔孔径尺寸设置不合理,没有达到预期的效果,阻尼腔内压力过大,超过工况要求,因此需要对快速启闭阀阻尼腔流场进行分析,并对泄压孔孔径进行优化设计,在达到阻尼目的的同时,降低峰值压力。
目前, 对于阻尼结构已经有大量的研究成果,多数关于阻尼机构的研究侧重于液压阻尼器和油缸结构的分析与优化[4~7]。王幼民以节流调速回路为设计工况,针对阀芯质量、阀芯工作面积及泄压孔液阻等变量, 应用复合形直接寻优算法,对P-B10B直动滑阀式溢流阀进行了参数优化设计[8]。 Ping Y设计制造了一种新型微流体耦合阻尼减振器,在试验的基础上,通过对减振器内部流体动力学现象的分析,建立了减振器的非线性动力学模型[9]。 杜恒和魏建华建立ADAMS/Simulink/AMESim联合仿真模型和多目标优化函数,并应用遗传算法进行联合仿真优化[10]。 王毅翔以轴向柱塞泵配流盘阻尼槽结构对配流过程的影响为研究对象,对多种不同的阻尼槽结构进行了精细的过流面积分析,并对阻尼槽结构参数进行优化[11]。 姚琳等推导出四轴连通油气悬架数学模型,建立了联合仿真模型,并应用遗传算法进行了优化设计[12]。 Zhang J H等使用带节流孔的阻尼套筒来改变阀门的内部几何形状,对作用在阻尼套筒阀芯上的流动力进行了实验和数值研究,以确定流场的差异对最小化力的影响[13]。 关于快速启闭阀内部阻尼结构性能和参数优化技术的研究却很少,笔者根据快速启闭阀内部结构和阻尼腔内部流体动力学现象,基于能量方程建立该阀的阻尼结构动力学模型,采用遗传算法对阻尼腔泄压孔孔径参数进行优化,优化结果不仅满足了阻尼速度和阻尼行程要求,而且降低了峰值压力。
1 阻尼腔的工作原理
快速启闭阀结构复杂,阀体内设计不同介质腔,笔者综合快速启闭阀工作情况,针对阻尼腔进行研究。 图1为阻尼腔部分结构示意图,当阀门开启时,活塞端部高速运动至行程末端,腔内的油液升压并经泄压孔流出,使活塞减速以抵抗活塞的惯性力及其他外力的作用而实现阻尼。
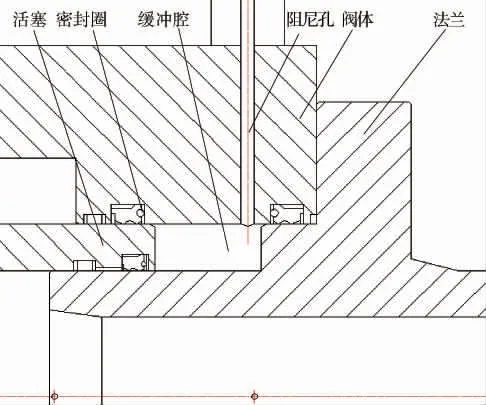
图1 快速启闭阀阻尼腔结构示意图
2 阻尼腔的动力学优化模型
为分析快速启闭阀阻尼过程动态特性,推导方程时做如下假设:阻尼过程是绝热过程[14];不考虑液油重力势能;整个阀体密封性良好,活塞与阀体之间无泄漏;不考虑由于油压升高而引起的液压油压缩量。
2.1 活塞受力平衡方程
阀瓣开启时受介质力向右运动,同时受阻尼腔油液阻尼压力和阀体内壁摩擦力作用,这里活塞所受的合力为F,此时活塞受力平衡方程为:

式中 A——活塞截面积,m2;
a——活塞加速度,m/s2;
F——活塞所受合力,N;
m——活塞惯性质量,kg;
P——阻尼腔油液压力,MPa。
2.2 流量方程
阻尼腔流量方程为:

式中 q——阻尼腔、节流口流量,m3/s;
v——活塞运动速度,m/s。
文中阀体阻尼腔符合厚壁泄压孔流量特性[15],泄压孔流量方程为:
式中 d——泄压孔孔径,m;
f——泄压孔面积,m2;
l——泄压孔孔长,m。
其中,ζ取1.49;λ为与Re有关的系数。
2.3 运动方程
阻尼过程中泄压孔孔径不变,活塞运动加速度为[16]:

式中 L——阻尼行程,m。
联立式(1)~(3)得活塞运动速度方程:
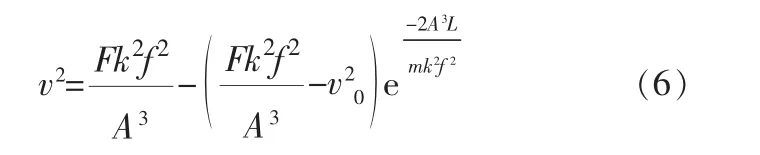
式中 v0——活塞初速度,m/s。
同时得到加速度方程:
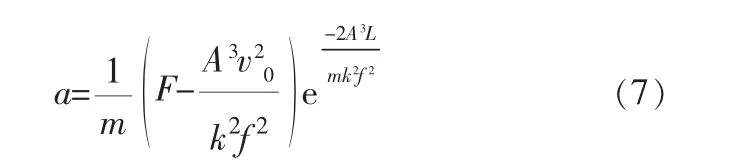
2.4 泄压孔结构及压力
由式(6)、(7)可知,活塞运动速度越大,加速度越大,所以最大加速度amax为:
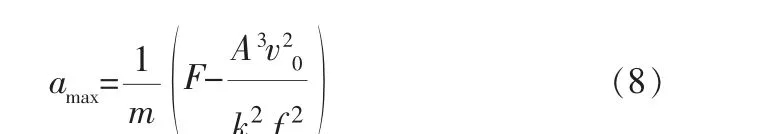
则阻尼腔泄压孔面积为:
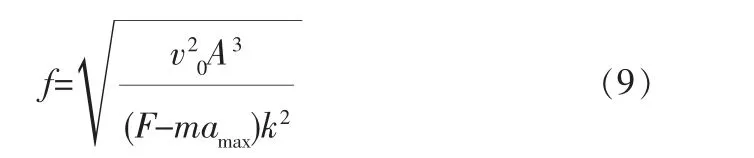
假设活塞在行程无穷大处加速度为零,但实际情况行程末端活塞加速度不为零[3],根据式(6)、(8)得到一个残余速度v∞为:
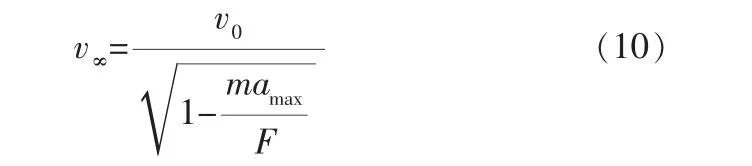
由此得到阻尼腔压力方程为:
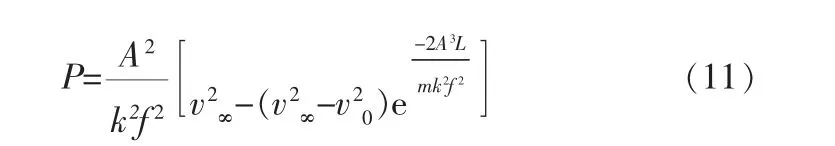
3 试验验证
3.1 试验过程
在整个控制系统中, 快速启闭阀气源来源于气体柱罐,如图2所示,在运行快速启闭阀之前,先对上游泵进行调试,在系统全压差达到上游泵开启压力时,其控制面打开上游泵,快速启闭阀阀芯开始作用,这时压力传感器P1开始作用(图3中的a点),当快速启闭阀满足开度要求时,阻尼腔液压油开始被压缩,这时压力传感器P2作用(图3中的b点),此时试验段结束,读出a、b两点的时间即可得出快速启闭阀开启时间。
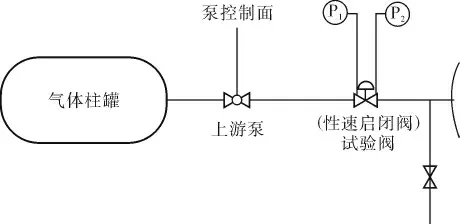
图2 试验流程简图
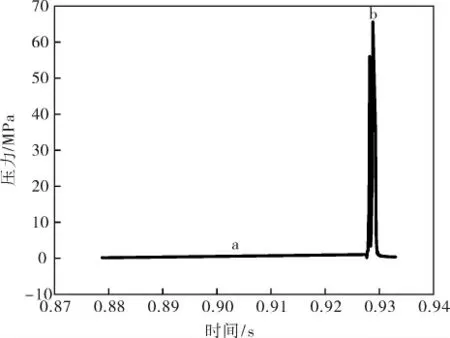
图3 阻尼腔试验压力曲线
3.2 试验验证
快速启闭阀的相关技术参数如下:
初速度v019.78 m/s
活塞所受合力F 766 383.3 N
活塞截面积A 0.10 m2
活塞惯性质量m 826.22 kg
泄压孔孔长l 0.21 m
油液密度ρ 856 kg/m3
试验泄压孔孔径d 0.050 m
测试峰值压力P 65 MPa
将参数带入理论模型中, 计算所得数据如下:
加速度a -927.57 m/s2
泄压孔面积f 0.001 8 m2
计算泄压孔孔径d 0.049 m
计算峰值压力P 65.56 MPa
由计算结果可以看出,计算的泄压孔孔径为0.049 m,试验泄压孔孔径为0.050 m,孔径近似相符。 理论计算阻尼腔压力曲线与试验油压曲线对比如图4所示。
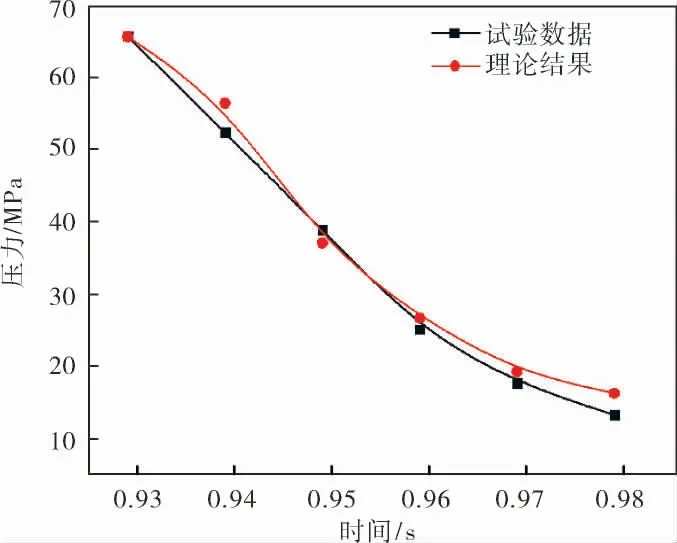
图4 阻尼腔压力曲线的理论结果与试验数据对比
从图4中看出, 理论模型计算得到的阻尼腔峰值压力与试验油液峰值压力相对误差小于5%,说明该理论模型准确。
4 阻尼腔参数优化中的遗传算法
遗传算法(Genetic Algorithms,简称GA或者GAs) 是由密歇根大学教授Holland J H和他的学生于20世纪60年代末到70年代初根据达尔文“自然选择,适者生存”的自然规律提出来的[17],是常用来解决多目标优化问题的一种优化方法,它是通过模拟自然界的生物进化过程,将遗传机制和生物进化论有机结合而形成的一种搜索最优解的算法[18]。
4.1 方法应用
由上述分析可知,快速启闭阀阻尼腔峰值压力约为65 MPa,为了降低峰值压力,缓解活塞端部对阀体的冲击,需要对泄压孔孔径进行优化设计。 笔者根据所建立的快速启闭阀优化模型和优化目标,采用遗传算法对泄压孔孔径进行优化。
基本遗传算法的操作步骤为:初始种群的产生;参数编码;适应度函数;遗传运算;控制参数设定。
每个个体被选中进行遗传运算的概率为该个体的适应值和群体中所有个体适应值总和的比例。 对于个体i,设其适应值为Fi,种群规模为NP,则该个体的选择概率表示为[17]:
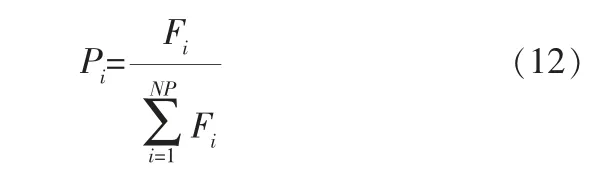
得到选择概率后,采用轮盘赌法来实现选择操作,得到每个个体的累积概率:

共轮转NP次,每次轮转时,随机产生ξk∈U(0,1),当PPi-1≤ξk<PPi时,选择个体i。
4.2 优化目标
运动惯性是产生压力冲击和机械结构振动的最主要原因,为避免机械冲击,又不产生过高的峰值压力,在其他条件不变时,利用遗传算法,以泄压孔孔径为优化参数来降低阻尼腔峰值压力,满足快速启闭阀阻尼腔设计要求。
4.3 约束条件
设置约束条件如下:
a. 依据文中的泄压孔流量方程和长径比定义可知[15]0.5<l/d<4.0;
b. 根据该阀的工况要求,阻尼腔压力允许值为P≤65 MPa;
c. 目标函数末速度应小于其初速度, 即v<19.78 m/s;
d. 受阀体空间限制, 阻尼行程L的约束条件为L<0.1 m。
4.4 结果分析
每代最优值对应的阻尼速度如图5所示,种群最优值在13代后趋于稳定,算法收敛,得到泄压孔孔径最优值,根据优化特征精度要求,笔者采用实数编码,初始种群由编码方法产生,对初始种群挑选出的染色体进行遗传运算时,交叉运算采用两点变交叉, 变异操作采用单点变异操作,用轮盘赌选择方法根据初始种群适应值计算得到概率。
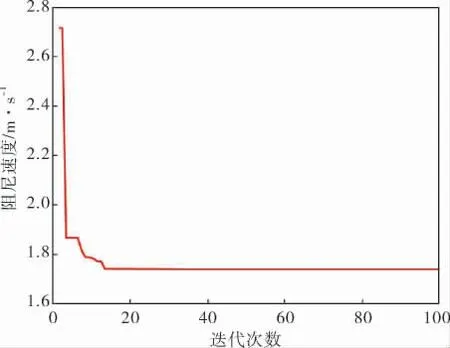
图5 每代最优值对应的阻尼速度曲线
遗传算法参数如下:
种群规模 200个
复制率 80%
最大代数 13代
变异率 10%
变异幅值 0.8
优化前后的参数列于表1。

表1 优化前后的参数
由表1看出优化后,泄压孔孔径增大,阻尼腔峰值压力降低,活塞速度增大,阻尼行程变长,优化前后压力与速度特性曲线随阻尼行程变化对比如图6、7所示。
由图6看出,优化前后,阻尼腔内的压力随着阻尼行程的增加而减小。 优化前腔内峰值压力高达65.56 MPa,优化后,泄压孔孔径增大,阻尼腔整体压力降低, 阻尼腔内峰值压力降为52.09 MPa,既可以满足结构强度要求,又确保了阀门的安全性。 由图7看出,随着阻尼行程的增加,快速启闭阀活塞运动速度逐渐减小。 优化前活塞的运动速度降低很快,优化后活塞运动速度降低缓慢,达到了缓冲的效果。
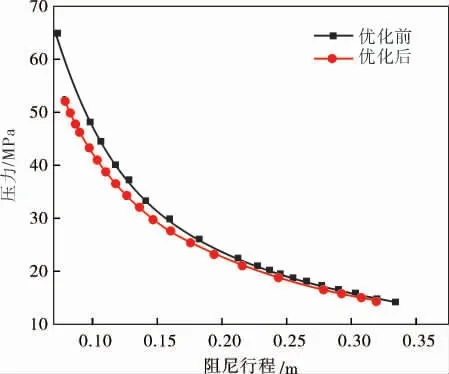
图6 阻尼行程-压力曲线
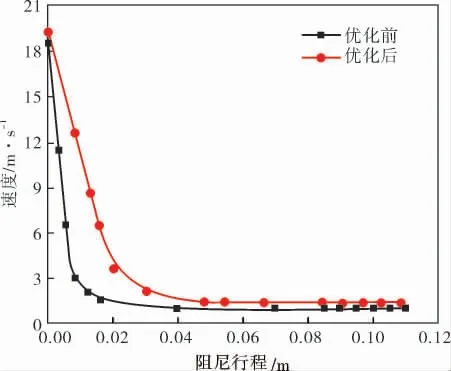
图7 阻尼行程-速度曲线
综上所述, 采用遗传算法优化阻尼孔径后,腔内峰值压力比原来降低了20%, 活塞运动速度由19.78 m/s减缓至1.74 m/s,快速启闭阀阻尼腔内特性曲线趋于平缓,整个系统运行稳定。
5 结论
5.1 基于能量方程建立了理论模型, 计算得到了阻尼腔泄压孔尺寸和压力峰值。与试验压力峰值的相对误差小于5%,证明理论模型的准确性。
5.2 通过采用遗传算法对泄压孔孔径进行了优化,得到阻尼腔孔径为0.053 m时,阻尼腔峰值压力降低了20%, 活塞运动速度减缓至1.74 m/s,达到了优化的目的。
5.3 通过结构优化,减小了快速启闭阀阻尼腔压力,即减缓活塞端部对阀体的冲击,从而有效提高阀门的可靠性和工作寿命。
