超轻量级所有权转移算法研究
2021-10-28谢海宝
谢海宝,吕 磊
(1.河南省市场监督管理局信息中心,河南 郑州 450008; 2.河南工业大学 信息科学与工程学院,河南 郑州 450008)
0 引 言
射频识别技术近些年伴随云计算、大数据、物联网等新技术的产生而得到进一步发展[1-2]。一个经典的RFID系统至少包含电子标签、读卡器、数据库三部分,电子标签在使用过程中,电子标签拥有者可能经常发生变化,拥有者发生变化之后,之前用户在电子标签里存放的隐私信息对当前用户来说应该是无权限访问之前用户存放的隐私信息[3-5]。为确保标签中隐私信息的安全,所有权转移协议是当前的热点研究方向。
文献[6]中STATIO等人首次提出标签所有权转移协议,并在该文献中设计一个所有权协议,协议引入可信第三方参与消息交换,具备一定安全性及一定价值意义。文献[7]中作者针对文献[6]的协议进行安全分析,指出该协议无法保证标签原所有者隐私信息的安全性,同时协议因缺少存放前后两次会话密钥,无法抗攻击者发起的去同步化攻击。文献[8]利用可信第三方设计一个协议,协议虽基于对称加密算法对隐私信息进行加密,但文献[9]指出文献[8]的协议存在攻击者可分析出下轮会话消息值可行性,即协议存在无法提供前向安全性的不足。文献[10]利用可信第三方,同时结合哈希函数给出一个协议,但文献[11]指出文献[10]的协议无法保障用户后向隐私安全性,同时加密算法的选择使得协议推广受到局限性。文献[12]给出一个改进的协议,并对协议进行分析,得出协议仍无法提供去同步化攻击安全性。文献[13]给出的协议,虽是采用优化后的RABIN算法对信息进行加密,对优化后的RABIN算法实则还是模运算,使得计算量较大,同时文献[13]的协议设计过程中步骤计算冗余,增加了标签端计算量。
鉴于较多协议存在计算量大或无法提供相对应的安全需求等不足,文中给出一个超轻量级的所有权协议。先自定义设计一个创新型的加密算法,即异或交叉运算,将在下一章节给出该加密算法详细设计过程。结合算法实现描述,可以知晓算法基于位运算实现,能够降低计算量,使得设计协议能够使用在计算受限制的标签中。协议中引入标志位STATUS信息,将根据该信息量得知标签归属者,具有唯一性。将文中算法与其他算法在相同环境下进行仿真实验,仿真数据表明文中算法能够弥补其他算法存在的安全不足之处,同时在大规模电子标签信息交互时,文中算法在计算时间开销角度具备较大的优势,计算时间复杂度要少于其他算法。
1 超轻量级算法
1.1 异或交叉运算定义
异或交叉运算(exclusive or cross operation,ECO(X,Y))按如下方式实现:
(1)X、Y、Z、T都表示二进制序列,长度都为L位;
(2)Wt(X)、Wt(Y)分别表示二进制序列X、Y的汉明重量;
(3)Px、Py分别表示指向二进制序列X、Y的指针;
(4)当Wt(X)≥Wt(Y)时,对二进制序列X、Y分别同时从第一位开始遍历,当指针Px指向二进制序列X的第i位Xi时,指针Py同时指向二进制序列Y的第i位Yi,将Xi和Yi数值进行加法运算,结果为偶数,则Xi和Yi进行异或运算,并将运算结果放置于二进制序列Z的第i位上,得到Zi;否则,将Xi放置于二进制序列Z的第i位上,得到Zi;
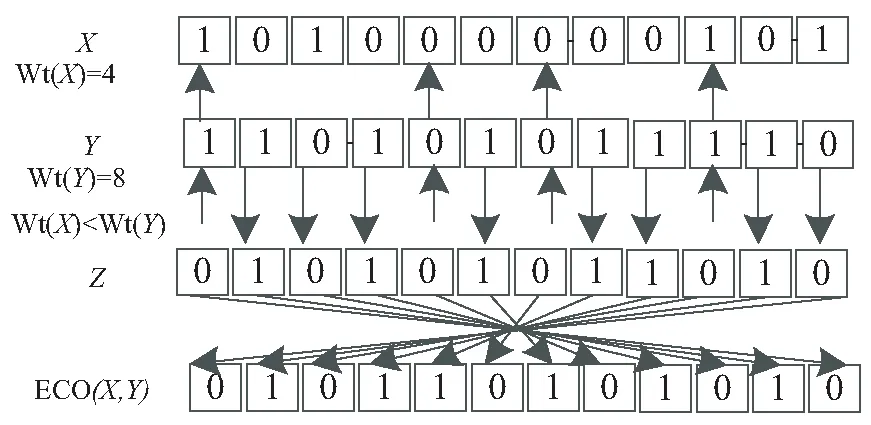
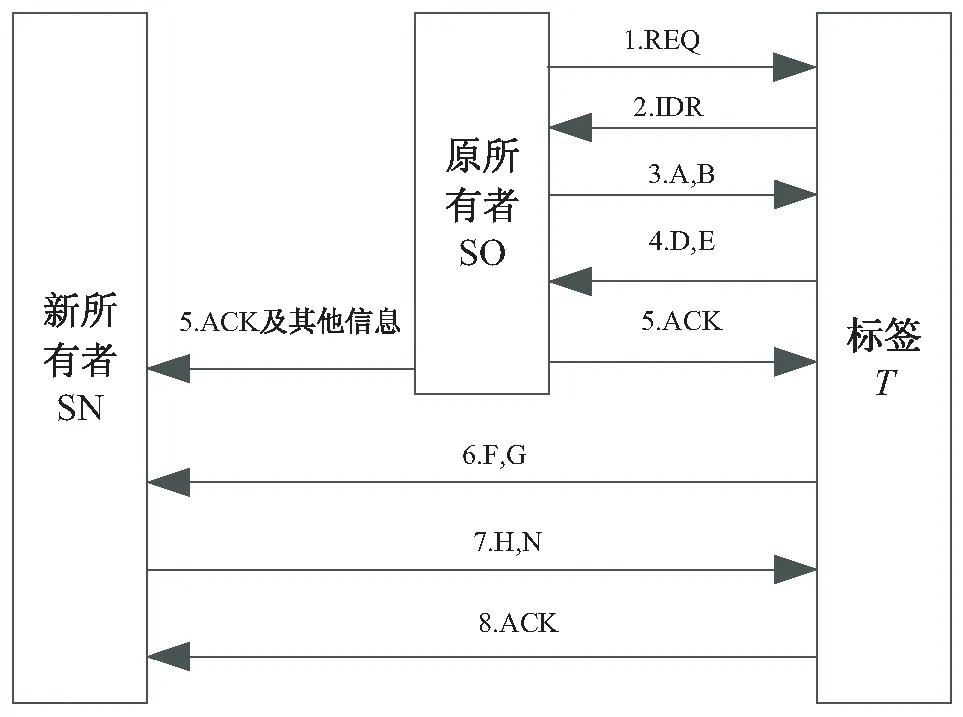
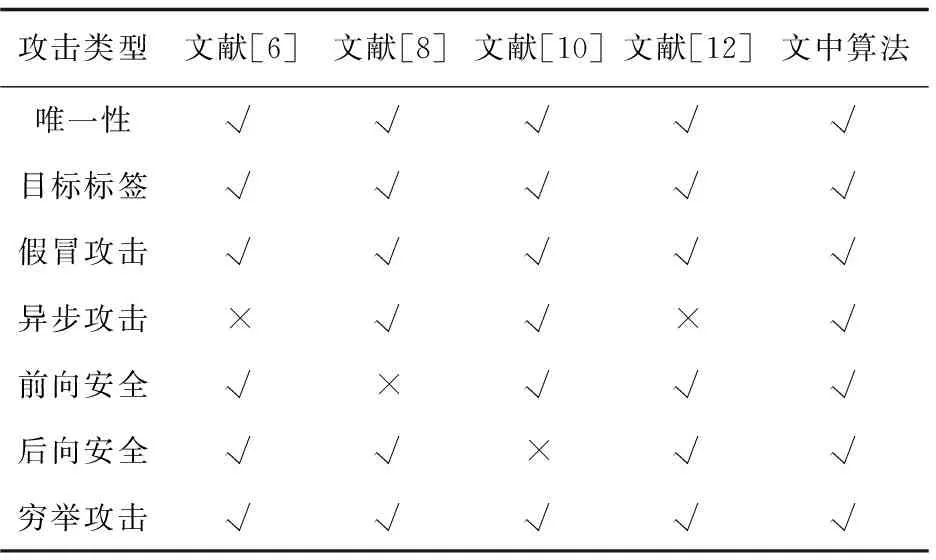
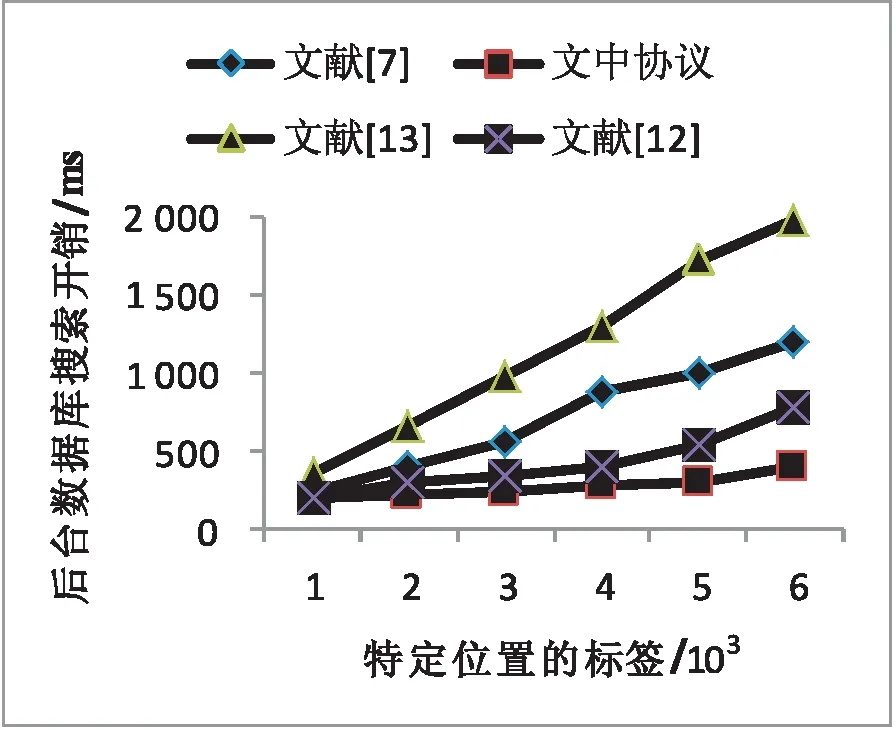
(5)当Wt(X) 通过两个例子对上述异或交叉运算进行解释。取值L=12位,X=001011100110,Y=010000100001,则可以得到Wt(X)=6、Wt(Y)=3,满足Wt(X)≥Wt(Y)条件,按照(4)中操作所得到异或交叉运算的结果为ECO(X,Y)=Z=001011000110。具体过程见图1。 图1 ECO(X,Y) Wt(X)≥Wt(Y) 再次取值L=12位,X=101000000101,Y=110101011110,则可以得到Wt(X)=4、Wt(Y)=8,满足Wt(X) 图2 ECO(X,Y) Wt(X) 异或交叉运算破解的难度在于:其一,参与加密运算的两个参数信息攻击者不知晓,则无法进行后续的破解操作;其二,即便是攻击者可以获取部分参与加密的参数信息,但攻击者仍无法具体获悉两个参数汉明重量具体数值为多少,则攻击者不会知晓按照哪种方式进行交叉异或运算。因此,基于上述分析,新设计的异或交叉运算可以提供较好的安全需求,确保加密参数信息的安全性。同时,异或交叉运算在按照上述定义实现过程中,是基于位运算实现的,可以使得加密算法的计算量得到大幅度降低,从而使得算法可以得到超轻量级的级别,能够适用于低成本的RFID系统标签中。 SN表示标签新所有者; SO表示标签原所有者; T表示电子标签; IDL表示T标识符左半边; IDR表示T标识符右半边; STATUS表示T所有权归属标志位,当STATUS=0时,表示所有权归属者为SO,当STATUS=1时,表示所有权归属者为SN; a表示SO产生的随机数; b表示T产生的随机数; c表示SN产生的随机数; K表示SO与T之间共享密钥; KO表示SO与T之间当前共享密钥; KO1表示SO与T之间上轮共享密钥; KT表示SN与T之间共享密钥; REQ表示请求命令; ACK表示确定命令; ⊕表示异或运算; &表示与运算; ECO(X,Y)表示异或交叉运算。 类似其他算法[14-16],做出如下假设规定:SN与SO之间通信安全,SN与T之间通信存在隐患,SO与T之间通信同样存在隐患。文中超轻量级协议示意图见图3。 图3 所有权转移算法实现过程 文中设计算法具体步骤如下: STEP 1 由SO向T发送REQ请求命令开启所有权转移算法。 STEP 2 T接到消息,查阅归属权标志位STATUS值,当前STATUS值为0,表示当前所有权归属于SO,因此T将IDR发送给SO以作为响应。 STEP 3 SO接到消息,在数据库中查询是否存在与IDR相等的值,未找到,SO对T验证失败,算法停止。找到,SO立刻生成随机数a,接着分别计算会话消息A、B,最后将A、B传送给T。 其中A=a⊕IDL、B=ECO(a,IDL)。 STEP 4 T接到消息,对A进行变形处理得到a'=A⊕IDL,将a'再结合IDL进行相同运算法则计算得到B',再对比B'与B。B'≠B,算法停止。B'=B,表明a'=a,且T验证SO通过,T马上生成随机数b,再分别计算D、E消息,最后将D、E发送给SO。 其中a'=A⊕IDL、B`=ECO(a',IDL)=ECO(A⊕IDL,IDL)、D=b⊕K、E=ECO(b,a)。 STEP 5 SO接到消息,对D进行变形处理得到b'=D⊕KO,将b'再结合KO进行相同运算法则计算得到E',再对比E'与E。 E'≠E,则SO将用KO1替换KO再次计算得到E'',并再次对比E''与E。仍不等,算法停止;若E''=E,表明SO对T验证通过,接着SO将向T发送ACK消息,告知T接下来可以与SN之间进行会话,同时SO向SN发送T相关信息及ACK消息,告知SN做好与T进行会话的准备。 E'=E,表明SO对T验证通过,接着SO将向T发送ACK消息,告知T接下来可以与SN之间进行会话,同时SO向SN发送T相关信息及ACK消息,告知SN做好与T进行会话的准备。 其中b'=D⊕KO、E'=ECO(b',a)=ECO(D⊕KO,a)、E''=ECO(b',a)=ECO(D⊕KO1,a)。 算法实现过程中,可能受到外界干扰或攻击者的蓄意破坏,使得算法中T与新旧所有者间短暂失去一致性,因此需要通过该步骤再次实现两者间的一致性。SO首先用KO验证,如果验证失败,此时有可能是会话实体两端短暂失去一致性,则SO将立刻用KO1替换KO再次发起验证,再次验证通过,则就可以恢复二者之间的一致性。 STEP 6 T接到消息,T开始计算F、G消息,并向SN发送F、G。 其中F=b⊕IDL、G=ECO(b,KT)。 STEP 7 SN接到消息,对F进行变形处理得到b'=F⊕IDL,将b'再结合KT根据相同运算法则计算得到G',再对比G'与G。G'≠G,算法停止。G'=G,表明b'=b,且SN验证T通过,SN马上生成随机数c,再分别计算H、N消息,最后将H、N发送给T。 其中b'=F⊕IDL、G'=ECO(b',KT)=ECO(F⊕IDL,KT)、H=c⊕(b&IDL)、N=ECO(KT,c)。 STEP 8 T接到消息,对H进行变形处理得到c'=H⊕(b&IDL),将c'再结合KT根据相同运算法则计算得到N',再对比N'与N。N'≠N,算法停止。N'=N,表明c'=c,且T验证SN通过,T将所有权归属标志位STATUS值由0置为1,表明T所有权发生变更,变更后T所有权归属者变为SN所有,最后T向SN发送ACK命令。 其中c'=H⊕(b&IDL)、N'=ECO(KT,c')=ECO(KT,(H⊕(b&IDL)))。 其中T一端的所有权归属标志位STATUS的值,攻击者是无法通过物理手段修改的。当且仅当,只有通过上述方式正确通过T的验证之后,T一端才会进行对所有权归属标志位STATUS的值的变动修改,从而可以保证T归属权的归属者唯一性。 STEP 9 SN接到消息,看到ACK命令,SN得知当前自己已获取T的所有权归属权限。 文中算法主要的创新点或优势在于:其一,给出一种新的信息加密方式,即异或交叉运算;其二,对于新的信息加密方式,不仅给出详细定义及实现步骤,同时结合具体实例进行分析;其三,所有信息全部采用密文方式发送,即信息先加密再发送,使得攻击者难以破解;其四,摒弃冗余的计算步骤,简化算法实现步骤,提高算法效率。 (1)所有权唯一性。 需确保不论何时标签所有权归属者必须具备唯一性,不能出现某个时刻存在有两个或两个以上所有权归属者。文中算法设计过程中引入归属权标志位STATUS,依据STATUS值来确定标签当前归属者。攻击者无法修改标签端STATUS值,标签端想修改STATUS值需通过若干轮会话验证,而攻击者无法通过验证,因此算法具备所有权唯一性要求。 (2)目标标签。 某用户可能某个时刻拥有多个标签的所有权限,当某标签所有权需进行转移时,要确保待转移的标签即为目标标签。文中协议前面几个步骤便是原所有者SO与标签T之间的相互认证过程,当且仅当两者相互认证都通过,才会进行T与SN之间的消息交换,从而可以确保待转移的标签即为目标标签。 (3)假冒攻击。 系统整个会话过程中,任何一个会话实体都可能被攻击者假冒,从而发起假冒攻击。文中算法在SN与T之间、SO与T之间进行消息交互时,先对消息来源方进行验证,验证失败,算法就停止,只有验证通过,才会进行后续操作,因此攻击者发起的假冒攻击肯定失败。 (4)去同步化攻击。 在SO与T交换消息的过程中,为抵抗攻击者发起的去同步化攻击,在SO端特地存放有当前以及上轮会话过程用到的共享密钥信息。SO首先用当前密钥发起对T的验证,验证通过,则进行后续操作;验证失败,SO在采用上轮会话密钥再次发起对T的验证,通过前后两次验证,可以抵抗攻击者发起的去同步化攻击。 (5)后向安全性。 攻击者通过某种手段获取整个会话消息,通过对获取的消息进行分析,获取之前某轮会话中的隐私信息,从而造成用户隐私信息泄露。文中算法为确保攻击者无法分析出之前会话隐私信息,加密过程中混入随机数,随机数前后两次值不同,攻击者在不知晓上轮及本轮随机数情况下,攻击者根本无法分析出之前加密隐私信息,因此算法具备后向安全性。 (6)前向安全性。 攻击者通过某些手段获取当前会话消息,企图对获取消息进行分析,从而预测下一次会话消息,并提前计算好下轮会话消息,通过一方认证。文中算法通过加密消息过程中混入随机数的方式来抵抗攻击者的攻击,因混入随机数,可以使得每轮会话过程中消息具备新鲜性,即每轮消息值不同,因随机数是随机产生,无规律性,因此攻击者无法提前预测下轮会话消息值,从而算法具备前向安全性。 (7)穷举攻击。 穷举攻击也可以称之为暴力破解攻击,即攻击者采用超级计算机对获取的密文进行穷举的方式穷举出所有可能的情况,从而破解出隐私信息。穷举攻击需要考虑成本开销,同时也需要考虑时间开销,不论是成本开销,还是时间开销,只要其中任意一个开销过大,则攻击者采用穷举攻击就代价过大,得不偿失。 文中算法一个完整通信过程被攻击者监听,则攻击者可以获取该通信过程中所有会话消息。这里选择消息A=a⊕IDL、B=ECO(a,IDL)为例进行穷举攻击分析。攻击者可以对消息A进行变形,然后带入消息B中,可得到B=ECO(A⊕IDL,IDL),在变形处理之后的B中,对于攻击者来说,看似好像只有IDL一个参量信息不知晓,攻击者以为可以穷举出IDL的值,但攻击者至少还有两个参量不知晓。其中一个是IDL参量自身携带的汉明重量值;另一个是A⊕IDL运算结果自身携带的汉明重量值。攻击者不知晓上述两个参数值,则无法在加密过程中涉及到如何进行异或运算或交叉运算,则攻击者穷举失败。 综上,攻击者无法穷举出有用隐私信息,故文中算法可抵抗攻击者发起的穷举攻击,确保信息的安全。 将文中算法与其他部分经典算法进行安全性对比,对比分析结果见表1。 表1 算法间安全性对比 说明:表1中,√符号表示可以抵抗该种类型的攻击方式,×符号表示无法抵抗该种类型的攻击方式。 从一轮完整会话通信量、标签端计算量对多个算法进行对比分析,见表2。 表2 算法间性能对比 针对表2中出现的符号给出下面的含义说明:Ha表示位运算(比如异或运算)的计算量大小,Hb表示异或交叉运算的计算量大小,Hc表示模运算的计算量大小,Hd表示哈希函数的计算量大小,He表示物理不可克隆函数的计算量大小,Hf表示产生随机数的计算量大小。L表示会话消息的长度,La表示会话过程中相关命令长度(比如REQ命令等)。 文中算法一轮完整会话消息包含IDR、A、B、D、E、F、G、H、N以及SO向SN发送的内容同10L;另外还包含一个REQ命令、三个ACK命令,共计4La,因此文中算法一个完整会话的通信量为10L+4La。 标签端计算量由来:计算a'过程中第一次用到Ha、计算消息D过程中第二次用到Ha、计算消息F过程中第三次用到Ha、计算c'过程中第四次、第五次用到Ha(其中一次是按位异或运算,另一次是按位与运算),共计用到五次Ha运算。计算B'过程中第一次用到Hb、计算消息E过程中第二次用到Hb、计算消息G过程中第三次用到Hb、计算N'过程中第四次用到Hb,因此共计用到四次Hb运算。算法在整个过程中T需要产生一个随机数b,因此需要用到一次Hf运算。基于上述,文中算法标签一端总计算量为5Ha+4Hb+Hf。 从表2中可以看出,从通信量角度出发,文中算法与其他算法大致相当;从标签端计算量角度出发,文中算法具有较大的改进,原因在于文中算法采用超轻量级自定义的加密算法,而没有采用传统的类似哈希函数、模运算等加密算法,同时文中算法可以弥补其他算法在安全性方面的不足。 文中选择后台数据库搜索特定标签成功所花费时间指标进行性能分析。好的加密算法,除了会话实体计算量减少之外,也会带来后台数据库对标签搜索时间的降低。 进行仿真实验相关的实验环境如下:电脑选择惠普笔记本、2013年9月购买、I 5处理器、内存2 GB、硬盘500 GB;以C语言作为仿真实验过程中部分算法编程实现的语言;选择小型数据库MySQL用来存放仿真实验过程中产生的相关数据;用MATLAB软件作为仿真实验用到的仿真平台。 系统在一个时间段内会对多个标签进行会话,单个标签与系统进行会话时,标签被搜索成功的时间长度会存在一定的差别。为减少误差,提升仿真实验的准确性,仿真实验时,假定系统中共有6 000个特定标签,依次对每组不同数量(1 000个、2 000个、3 000个、4 000个、5 000个、6 000个)的标签进行200次搜索,记录每一次搜索成功时间值,并求取平均值作为最终的仿真实验结果。 将文中算法与文献[7,12-13]中的算法在相同的仿真实验环境下进行仿真实验,绘制出如图4所示的仿真结果。 图4 特定位置标签数量与搜索时间开销对比 从图4中可以看出,最开始标签数量不多的时候,后台数据库搜索时间相差不大。但随着搜索标签数量的不断增加,不同算法中后台数据库搜索标签成功的时间都在增加,但各算法增加的趋势并不相同。可以看出,文献[7,13]中算法随着标签数量增多,搜索标签时间几乎成线性增长;而文献[12]中算法搜索时间相对于上述算法搜索时间有所降低,但与文中算法的搜索时间相比,文中算法的搜索时间仍优于文献[12]中算法的搜索时间。基于上述阐述,文中算法具备一定的推广使用价值及意义。 针对存放在电子标签中的隐私信息易泄露问题,文中设计一种超轻量级的算法。不同于其他算法,文中算法并未采用经典的哈希函数或PUF函数或伪随机函数对信息加密,而是采用一种自己设计的异或交叉运算算法实现信息加密;异或交叉运算将基于加密信息汉明重量不同进行不同方式的交叉操作,从而提升加密算法安全性,同时该运算设计思想基于位运算实现,使得文中算法整体计算时间开销得到一定程度的降低。通过理论及仿真实验将文中算法与其他算法进行对比分析,表明文中算法在安全性角度优于其他算法,能够弥补其他算法存在的安全缺陷,同时在性能上文中算法在对标签搜索时间开销上优于其他算法,降低了搜索时间开销。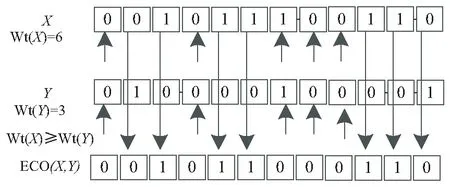
1.2 算法符号含义
1.3 算法具体设计
2 算法安全性分析
3 算法性能分析

4 算法仿真实验
5 结束语
