一种用于公共自行车调度的改进GA-SA算法

赵红梦，姜志侠，曾 坤

(长春理工大学 理学院，吉林 长春 130022)

0 引 言

随着中国经济的快速发展以及居民生活水平的不断提高，交通拥堵问题日益严重，为了更好地响应党中央绿色出行的号召，缓解城市交通压力，城市公共自行车应运而生。随着公共自行车的高效发展，一系列问题也逐渐显现，如由于调度不平衡导致租还车难的问题大大降低了用户对于公共自行车使用的满意度，对公共自行车进行调度优化的研究迫在眉睫；考虑到车辆的容量要求，如何设计节约成本的调度方案，最大程度地提高市民对公共自行车使用的满意度是亟待解决的问题。

目前学者对公共自行车单调度问题的研究主要分为调度模型和调度方法两大类。2005年任传祥等[1]提出混合遗传模拟退火算法解决公交车辆行车计划模型；2011年Mike Benchimo等[2]重点研究以调度运输费用最小为目标函数的车辆静态调度优化模型；2013年Daniel Chemla[3]用禁忌搜索算法解决静态公共自行车问题；2017年Fábio Cruz等[4]提出一种基于局部迭代的启发式算法解决单调度静态无时间窗优化模型；同年Aritra Pal[5]等提出了一种求解静态完全再平衡问题的混合整数线性规划模型，利用混合嵌套的大邻域搜索与可变邻域下降算法解决公共自行车调度问题；2017年栾英杰[6]提出一种GA-SA算法解决公共自行车调度问题。基于此，文中主要研究静态公共自行车调度问题，以成本最小化为目标建立调度模型，并利用改进的遗传模拟退火算法进行求解。

1 模型建立

文中要研究的单车场无时间窗调度问题可以描述为:在已知各租赁点之间的距离和调度需求的前提下，如何合理地安排调度车的调度路线，使行驶成本和车辆的固定成本最小。用有向图G=(N,E)表示公共自行车的调配网络，其中N={0,1,…,n}表示租赁点的集合，0表示调度中心，n为租赁点数目，E={(i,j)|i,j∈N,i≠j}表示相连租赁点的边集;V={1,2,…,K}表示调度车的集合，K为调度车辆总数目；用最大载重量Q的调度车,从调度中心出发，并且最终返回调度中心;其中租赁点i和租赁点j之间的距离dij和租赁点i的调度需求qi已知。

C0为调度车辆的固定成本，C1为单位距离配送费，调度车辆k被使用时记二进制变量ξk等于1，否则为0；xijk表示车辆路线安排，当车辆k在服务完i后再服务j时，xijk取1，否则xijk取0。

根据以上条件建立数学模型(PBVSP)：

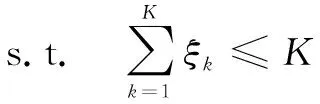
(1)

(2)

(3)

(4)

(5)

目标函数为成本最小化，成本包括行驶成本和车辆的固定成本，其中约束(1)表示从调度中心(车场)出来的车辆数量最大不超过K，约束(2)确保每个路线在调度中心开始或结束，约束(3)、(4)表示规定每个租赁点只能由一辆车进行访问，约束(5)表示每辆车上自行车的量不大于调度车辆的容量。

2 算法设计

遗传算法[7]具有强大的全局最优解搜索能力，并且收敛速度较快[8]，但是存在局部搜索能力差和早熟收敛等问题[9]；模拟退火算法具有摆脱局部最优解的能力，但算法运行效率不高，进化速度较慢；文中算法思想是基于这两种算法的特点，将其结合使用增强算法运行效率。针对公共自行车单调度问题(PBVSP)设计一种GA-SA算法，具体操作流程如下：

2.1 算法的变异操作

在进行染色体变异之前，首先对染色体进行编码，n个租赁点编码长度为n，染色体为1至n之间的随机整数排列，例如n为6，染色体可能为[1 3 4 5 6 2]。

变异的主要目的是保持群体的多样性，采用两两交换变异的方法，按变异概率pm选择需要变异的染色体，随机产生两个自然数n1和n2，交换第n1位和第n2位所对应的基因。例如n1等于2，n2等于5，初始染色体为[1 6 3 4 5 2]，经过变异后的染色体为[1 5 3 4 6 2]。

2.2 算法的交叉操作

文中提出基于经典两点交叉操作方法的三种改进方式，具体如下：

(1)基于关联度的两点交叉法。

在进行两点交叉操作之前对其基因间的关联进行判断，两个染色体X={x1,x2,…,xn}，Y={y1,y2,…,yn}，xi,yi∈{1,2,…,n}，n为租赁点数目，引入二进制变量δi。

判断X,Y之间关联度的公式如下：

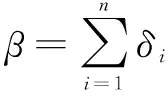
(6)

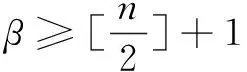
(2)修正重复元素的两点交叉法。

两点交叉首先随机产生两个父代染色体，如f1=[1 6 3 4 5 2]，f2=[4 3 2 6 5 1]，随机产生两个自然数n1和n2，对两个父代染色体n1至n2之间的基因片段进行交换，如n1等于2，n2等于4，得到两个子个体分别为[1 3 2 6 5 2]，[4 6 3 4 5 1]；对其进行修正：若交叉片段与非交叉片段中出现相同元素，则利用缺失元素去替换交叉部分重复元素，修正后的染色体为[1 3 4 6 5 2]，[4 6 3 2 5 1]。

(3)基于自适应的两点交叉法。

一般遗传算法两点交叉概率pc是设定好的，基于此，根据种群适应度的情况提出自适应交叉法。主要思想是对高适应度值的个体降低交叉概率，对较低适应度的个体提高交叉概率，以避免发散和陷入局部最优，并保持种群中较好的个体。文中提出自适应交叉的公式如下：

(7)

其中，α为自适应参数，fmax为个体最大适应度值，favg为个体平均适应度值；之后进行经典两点交叉。

2.3 算法的解码操作

在使用GA-SA算法解决PBVSP问题时，需要对一个编码F(染色体)进行解码，以便满足载重等约束条件，并得到多个子路径。具体方法见图1。

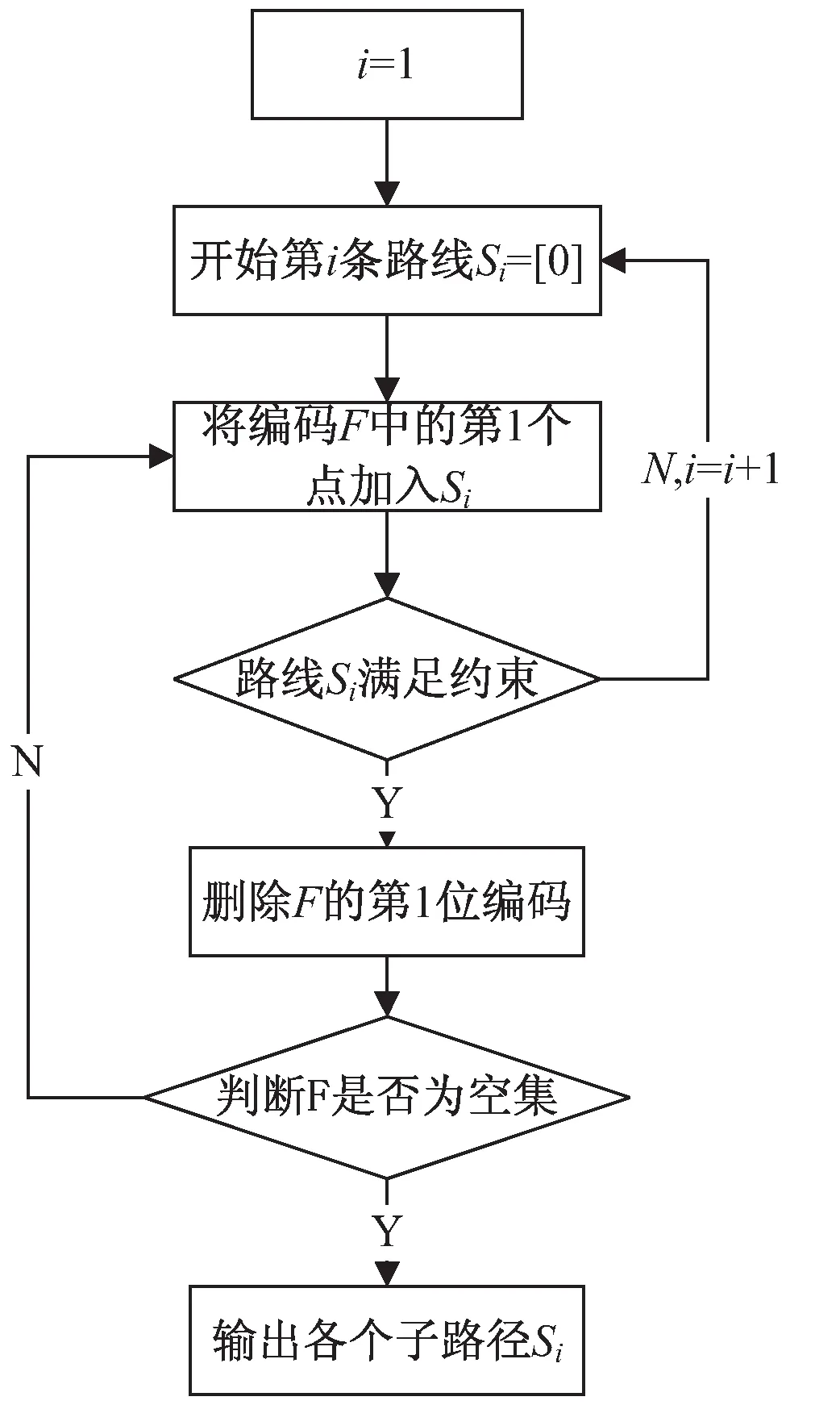
图1 染色体解码流程

举例分析，若公共自行车租赁点编码F为[1 3 4 5 6 2]，第一条路线，尝试将F中第一个点1加入路线S1，若加入后满足约束条件，S1变为S1=[0 1]，删除F中的1，将其第二个点3加入S1，若满足约束，S1=[0 1 3]，否则，开始第二条路线S2，依次类推直到F为空集时终止解码操作。

染色体进行解码后，计算适应度函数值，目标Z为求最小成本问题，染色体适应度函数设置为其倒数，如公式(8)所示。

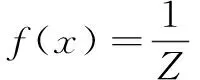
(8)

2.4 算法的选择操作

模拟退火算法[10]是一种基于概率的算法，该算法模拟了固体降温的过程[11]。它的出发点是结合物理退火与组合优化问题的相似性；基于此，文中将模拟退火算法引入到遗传算法的选择之中。

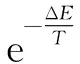
采用经典的轮盘赌选择方法，它是一种基于比例的选择方法，若某个个体i适应度为fi，种群大小为NP，则被选择的概率如公式(9)：

(9)

个体适应度越小，被选择的机会也就越小，反之亦然。

文中所提出的算法是以遗传算法为主体，融入模拟退火算法优化群体的选择，算法的具体流程如图2所示。

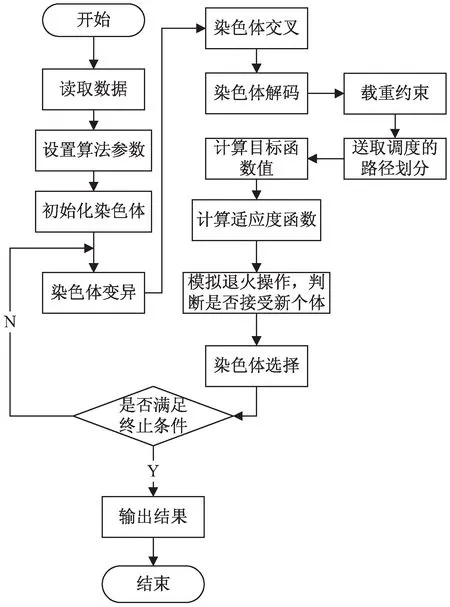
图2 算法流程

3 实例分析

研究的仿真数据[12]为纽约市公共自行车系统的运营公开数据，Citi Bike NYC网站上公布的纽约市公共自行车出行数据中的每个站点对应一个ID编号，选择400～423之间的21个ID号作为租赁点，其中400为调度中心0。各个租赁点调度需求与经纬度坐标见表1，其中正数表示本租赁点有多余的自行车数量，负值表示该租赁点需要供入自行车，调度车初始装载量为20。

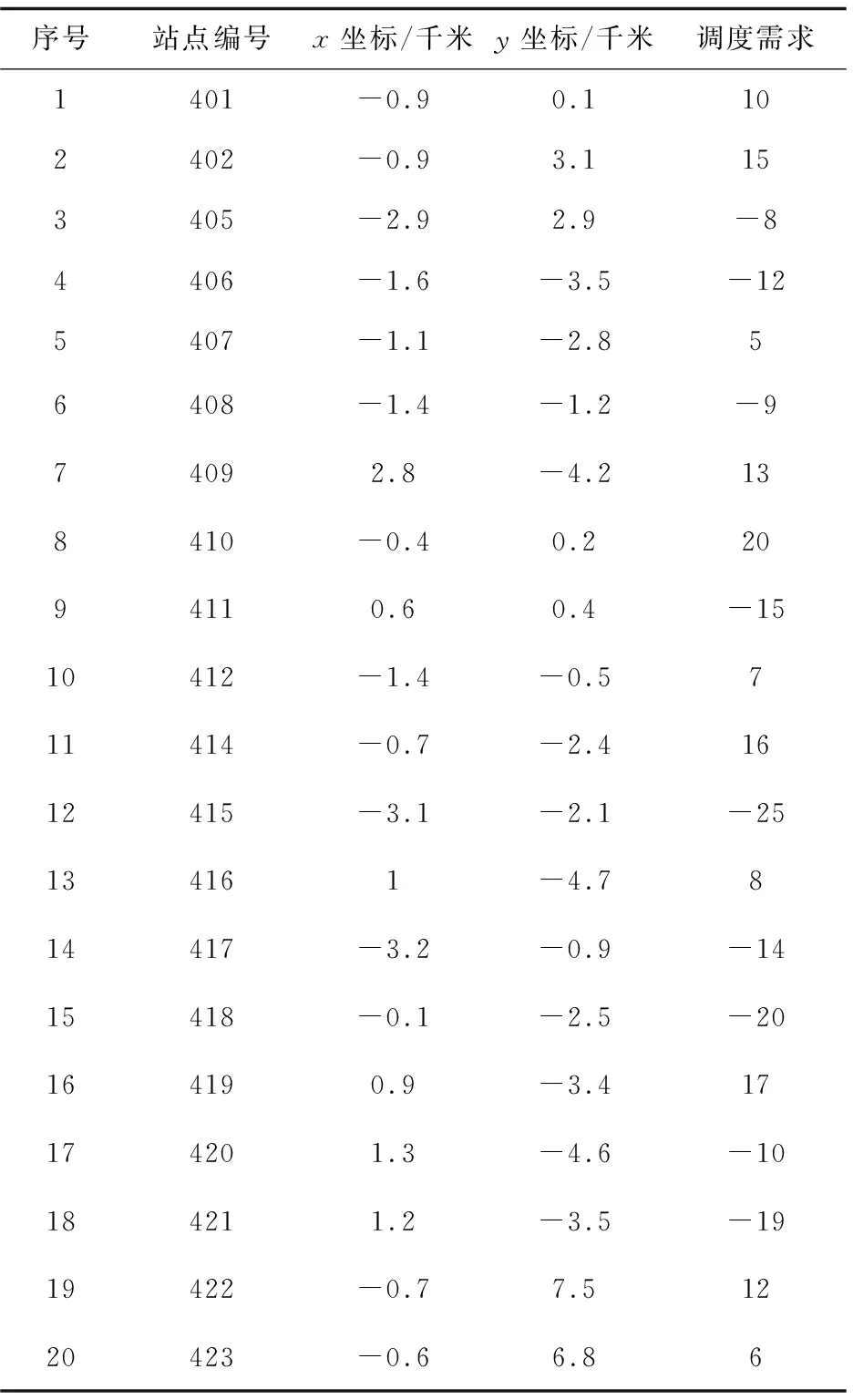
表1 原始数据

首先对参数进行设置，调度车固定成本C0为18，单位距离配送费C1为1，调度车容量Q为25，调度车总数目K为5，遗传算法种群数NP为100，遗传算法迭代次数maxgen为200，变异概率pm为0.1。

问题要求调度车从调度中心出发去租赁点取送公共自行车，并且最终返回调度中心。针对文中提出的GA-SA算法对PBVSP问题进行调度分析，其中交叉操作分别采用三种形式进行计算：基于关联度的两点交叉法、修正重复元素的两点交叉法、基于自适应的两点交叉法，具体三种调度结果如下：

基于文中算法，其中交叉操作选择基于关联度的两点交叉法，经MATLAB软件计算可得最小成本为131.649元(保留三个有效数字)，需要调度车辆4个，具体调度车路径为：第一个车辆调度的租赁点路径为：0-3-19-20-9-2-0，第二个车辆调度路径为0-8-12-5-11-0，第三个车辆调度路径为0-15-1-6-0，第四个车辆调度路径为0-4-16-18-7-17-13-14-10-0。算法的收敛曲线见图3。

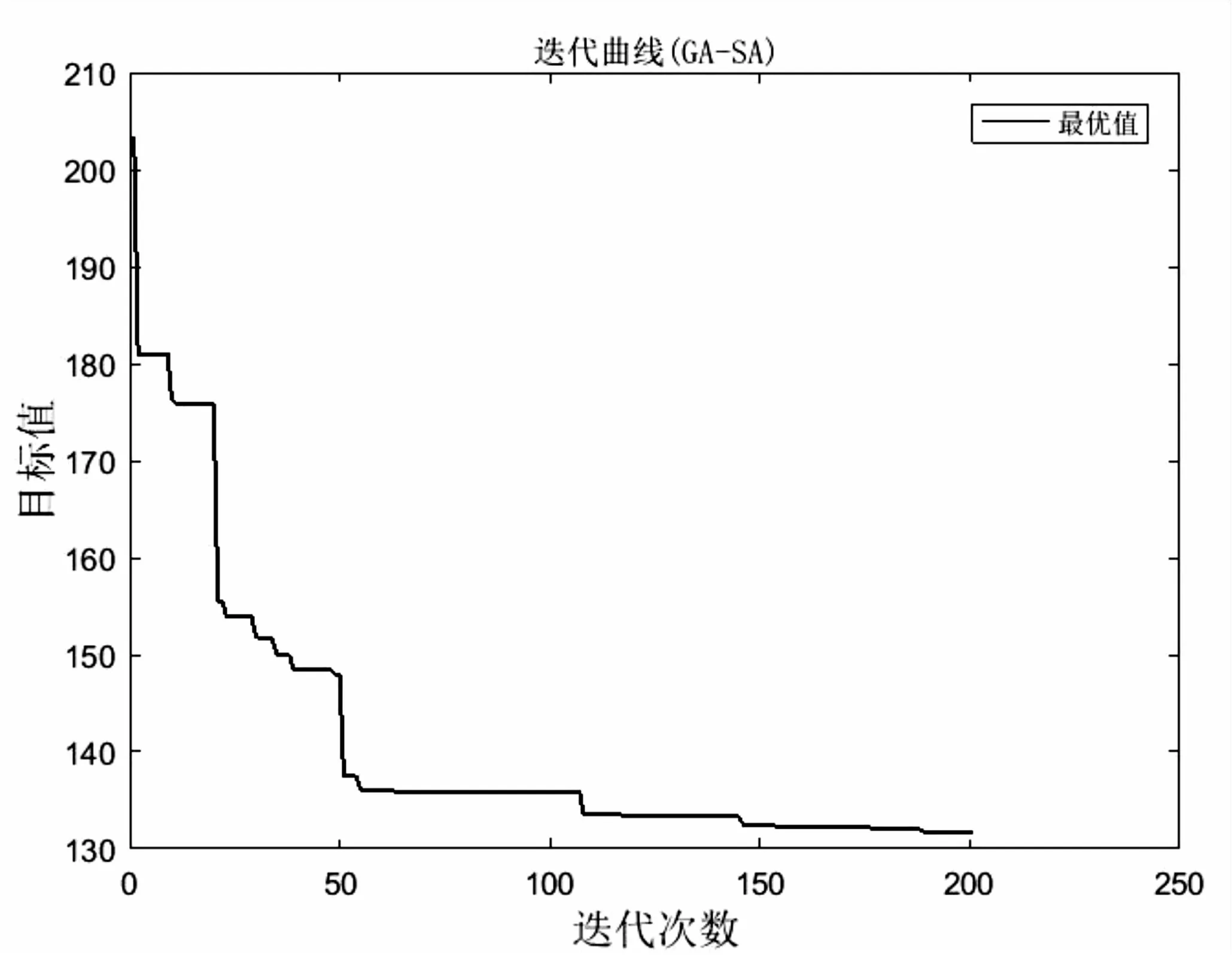
图3 第一种交叉方法迭代曲线

当算法交叉步骤选择第二种方法：修正重复元素的两点交叉法，经MATLAB软件计算可得最小成本为127.944元(保留三个有效数字)，需要4个调度车，具体调度车路径为：第一个车辆调度的租赁点路径为：0-8-9-2-3-14-10-0，第二个车辆调度路径为0-6-1-0，第三个车辆调度路径为0-5-12-20-19-0，第四个车辆调度路径为0-7-17-13-18-16-4-11-15-0。算法的收敛曲线见图4。

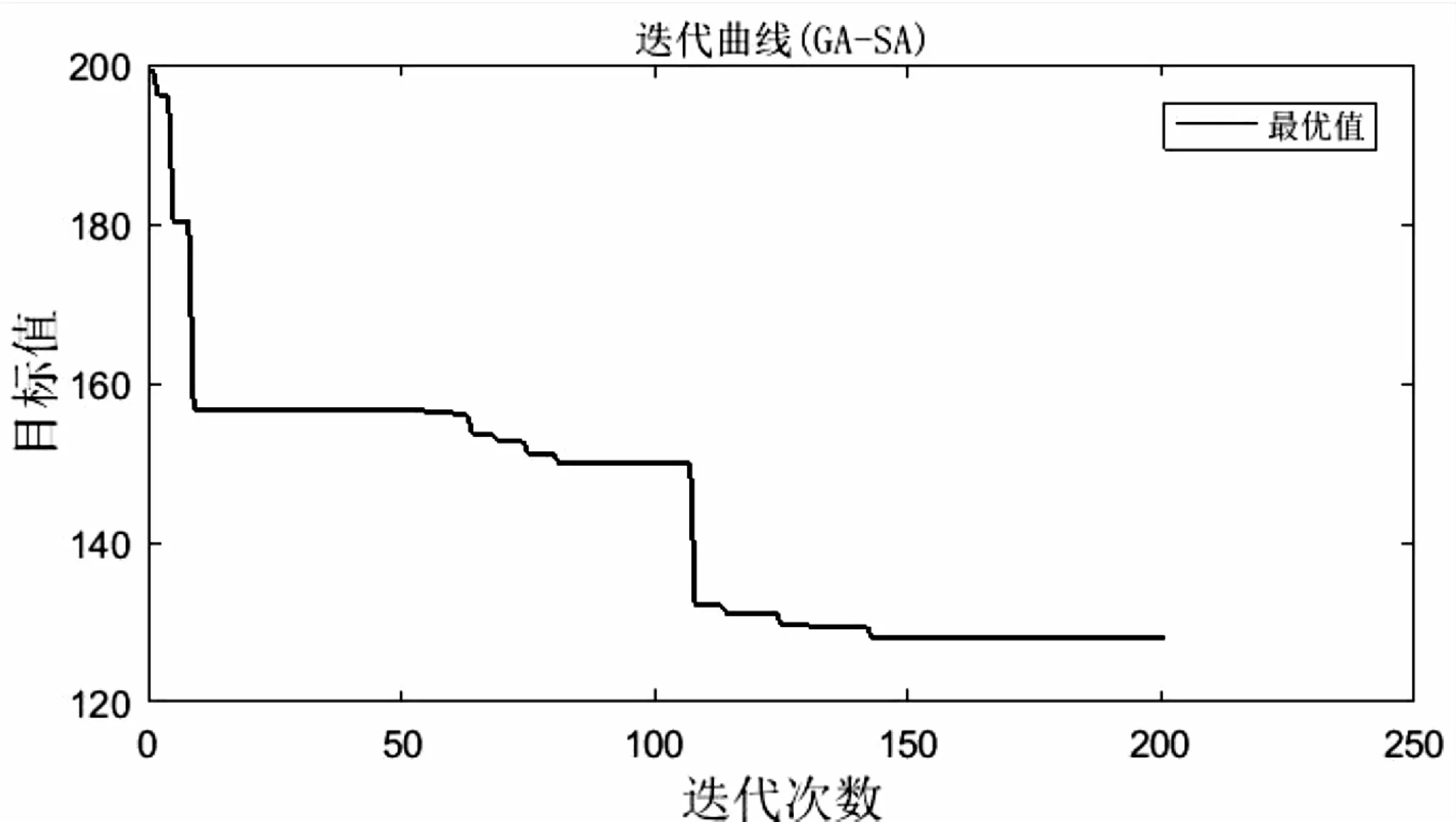
图4 第二种交叉方法迭代曲线

当算法交叉步骤选择基于自适应的两点交叉法，计算可得最小成本为135.093元(保留三个有效数字)，需要4个调度车，具体调度车路径为：第一个车辆调度的租赁点路径为0-2-12-1-6-8-0，第二个车辆调度路径为0-3-19-20-9-7-17-13-18-0，第三个车辆调度路径为0-15-11-14-10-0，第四个车辆调度路径为0-5-4-16-0。算法的收敛曲线见图5。

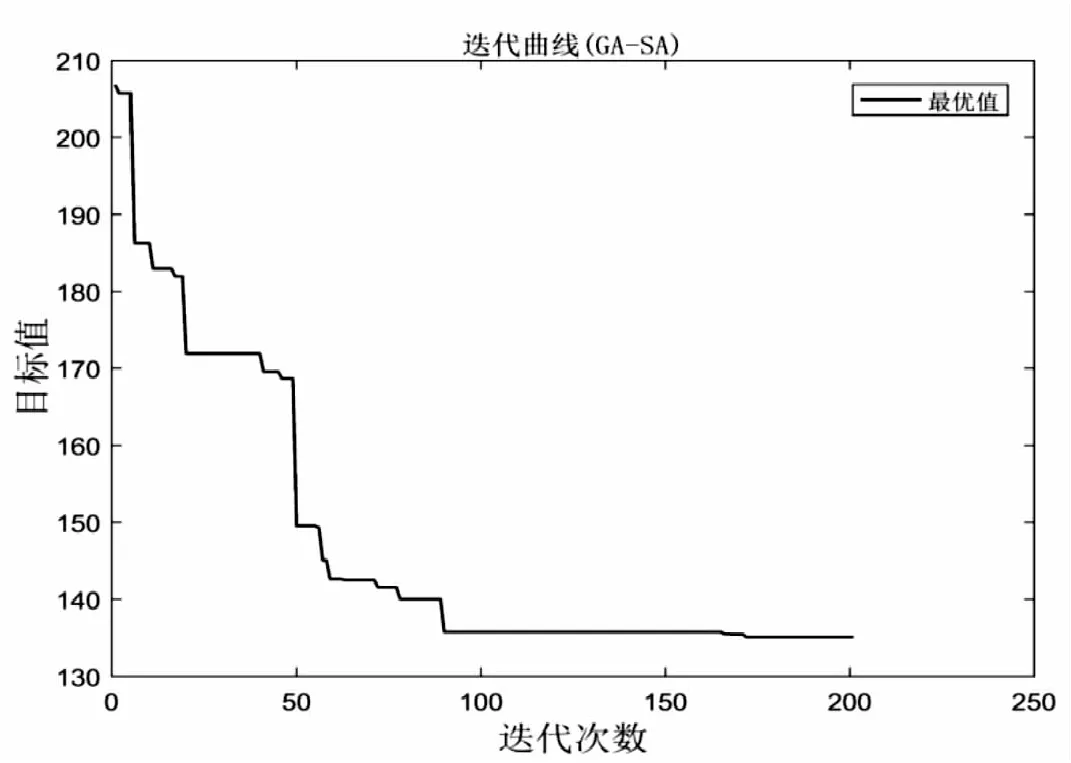
图5 第三种交叉方法迭代曲线

通过三种交叉方法对PBVSP进行计算，可知针对纽约市公共自行车数据，文中提出的GA-SA算法具有可行性并且效果良好。接下来对GA-SA算法(交叉选择修正重复元素的两点交叉法)和GA算法，以及文献[6]中的GA-SA算法进行对比分析。

利用三种算法分别对纽约市公共自行车出行数据进行10次计算，得出的结果见表2(结果保留三位有效数字)。

表2 算法结果对比

可以看出文中算法所得的平均成本为132.109 2，最优解为127.944，均小于其他两种算法的目标值，基于文中算法，GA算法和GA-SA算法的目标成本减少率见表3。

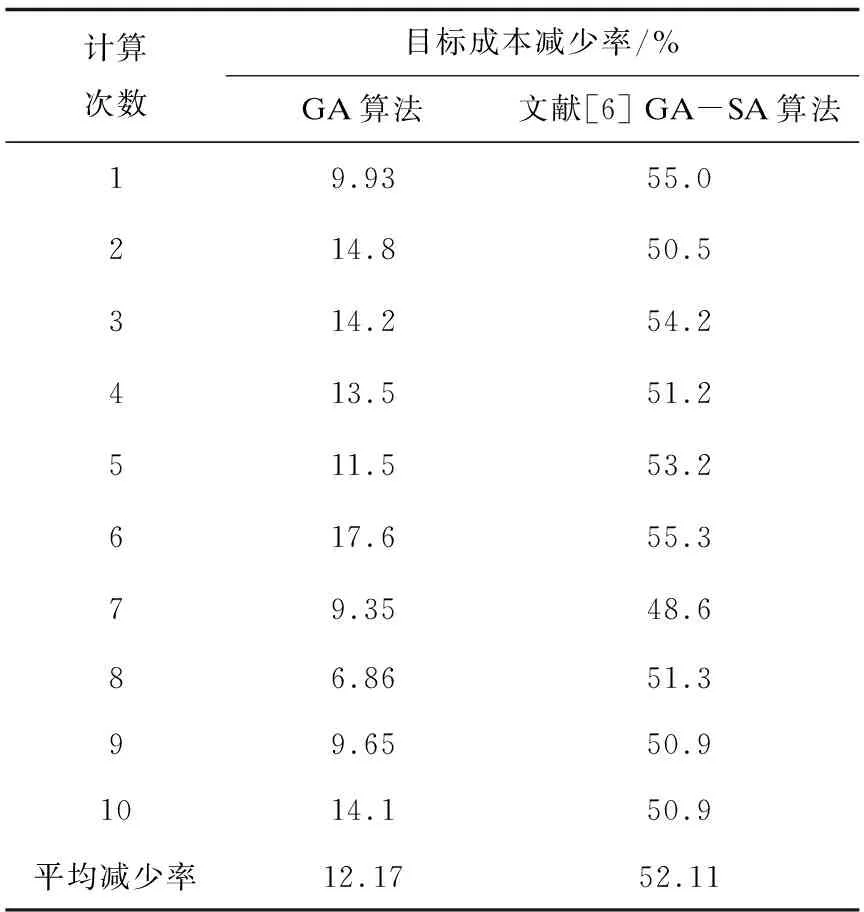
表3 算法的成本减少率

根据表3可看出基于文中算法，GA算法的目标值成本平均优化率达到了12.17%，文献[6]GA-SA算法平均优化率为52.11%，再一次验证文中算法适用于解决公共自行车调度问题。

另外利用t检验[13]来判断文中算法与GA算法、文献[6]算法之间是否存在统计上的显著差异，以文中算法和GA算法比较为例，采用t检验中的双总体检验法，给出原假设H0和备择假设H1分别为：

H0:μGA-SA-μGA=0

H1:μGA-SA-μGA≠0

其中，μGA-SA表示文中算法的均值，μGA为GA算法的均值。

计算检验统计量为：

(10)

表4 两样本检验

通过表4可以看出，显著性检验均为0<0.05,因此拒绝原假设，接受备择假设，文中提出的GA-SA算法和GA算法、文献[6]中算法在统计学上有显著差异。

通过以上分析研究，文中提出的算法在公共自行车调度问题上有较优的可行性。

4 结束语

建立了基于成本最小的公共自行车静态调度模型，采用改进的遗传混合模拟退火的GA-SA算法进行求解，通过实例分析表明：该算法的优化效果较好，有较强的可行性和有效性。伴随着路径优化问题的需求增大，在该研究的基础上综合考虑软时间窗[14]、多车场[15]等具体背景约束[16]，求解公共自行车调度问题是接下来的研究方向之一。