改进kmeans算法在学生消费画像中的应用

凌玉龙，张 晓，李 霞，张 勇

(1.西北工业大学 大数据存储与管理工信部重点实验室，陕西 西安 710129； 2.西北工业大学 学生资助服务中心，陕西 西安 710129)

0 引 言

学生群体肩负着祖国的未来，在社会中扮演着重要的角色，因此对学生的行为进行分析具有重大意义。数据挖掘作为一种从海量数据中获取潜在知识的技术，已经在各个领域取得广泛应用。采用数据挖掘技术挖掘学生消费数据中潜在的知识可以充分发挥现有消费数据的作用，为学校管理人员的决策提供数据支持。

作为最经典的数据挖掘算法之一，kmeans算法思想简单，易于实现，有着广泛的应用。随着社会的发展，出现了一系列使用传统kmeans算法难以解决的新问题和新场景，学术界针对传统kmeans算法不断进行改进以适应这些场景。例如，谢修娟[1]为了从微博数据中发现热点舆情，提出一种基于密度的初始聚类中心选择算法，改进算法在微博数据集上拥有更高的准确性和稳定性。马汉达[2]针对传统kmeans在Web日志挖掘中性能不高的缺点，提出了基于粒子群算法的改进kmeans算法,并在Hadoop上实现了并行化，实验证明改进算法不仅提高了聚类准确率，而且提升了运行效率。Lutz[3]为了解决kmeans算法在GPU上效能较低的问题，针对kmeans算法每次迭代计算质心的过程提出了一种新的算法来更新质心，改进后的kmeans算法提高了20%的吞吐量。

如何利用校园消费数据分析学生群体行为，实现贫困生精确资助，提高学生学习生活质量，保障学生安全，已经成为高校急需解决的问题。随着数据挖掘技术的发展，很多研究人员尝试将数据挖掘技术与学生行为分析相结合[4-13]，其中黄刚[14]和姜楠[15]的研究具有一定的代表性。这两位学者在学生校园消费数据集上采用kmeans算法对学生进行聚类，分析学生的消费习惯和群体特征，并进行了画像说明，为高校学生管理工作提供依据。但是他们的研究仅是将kmeans算法引入到学生行为分析领域，没有考虑学生消费数据集本身的特点和kmeans算法随机选择初始聚类中心的缺点。

文中根据学生消费数据集的特点和kmeans算法随机选择初始聚类中心的不足，提出一种基于马氏距离和密度的改进kmeans算法，并将其应用于西安某高校的校园一卡通消费数据集上，对学生群体行为进行分析并构建消费画像，从大数据的角度探究了学生行为，同时推动了贫困生精准资助领域的发展。

1 理论介绍

本节分析了学生消费数据集的特点和kmeans算法选择随机初始聚类中心的不足，针对kmeans算法提出两点改进以更好地适用于学生群体聚类场景。

1.1 欧氏距离和马氏距离

经典的kmeans算法采用欧氏距离计算样本之间的距离，欧氏距离单纯考虑数值上的距离，忽略了数据属性之间的依赖性，将数据各个属性之间的差别同等看待。但是大部分实际场景中的数据属性之间并不是独立的，各个属性起到的作用也各不相同。

马氏距离是欧氏距离的一种修正，其修正了欧氏距离中各个属性尺度不一致且相关的问题。马氏距离认为属性之间是存在联系的，所以在计算公式中引入了协方差。对于一个多变量向量x=(x1,x2,…,xp)T，设其均值为μ=(μ1,μ2,…,μp)T，协方差矩阵为Σ，则其马氏距离定义为：

(1)

其中，T表示矩阵的转置。如果数据之间独立同分布，那么对应的协方差矩阵就变成了单位阵，在这种情况下马氏距离就变成了欧氏距离。

马氏距离由于其设计思想会将某一微小变量的作用放大，这在某些应用场景中可能会导致结果的过拟合。但是不同于其他应用场景下的数据，学生群体是一个具有高度相似性的群体，由于课业的安排和学校的规章制度，大部分学生的生活作息规律极其相似，学生的就餐时间、就餐地点、消费情况相对固定且有规律，不同学生的行为相差较小。由于学生消费数据的特点和马氏距离的特点，该文认为采用马氏距离代替欧氏距离的kmeans算法更适合对学生消费数据进行聚类分析。

1.2 初始聚类中心的选择

kmeans算法是从样本集合中随机选择k个样本作为初始聚类中心，这种初始化聚类中心的思想没有考虑到数据的分布情况和离群样本点的影响，很可能会产生较差的聚类结果。虽然随机选择初始聚类中心的kmeans算法的聚类效果可能不好，但是无论初始聚类中心怎么选择，经过一系列迭代后得到的最终聚类中心的周边的点都是高密度点，即这些聚类中心周边的点都比较密集，不会存在离群样本点。

文中选择初始聚类中心的改进思想为：在高密度样本集上应用最小最大原则得到k个样本作为初始聚类中心。具体步骤如下：

(1)运行一次kmeans算法，得到k个聚类中心；

(2)选择与k个聚类中心距离最近的一定比例(记为percent)的样本作为高密度样本集；

(3)从高密度样本集中随机选择一个样本作为第一个初始聚类中心；

(4)从剩下的高密度样本集中选择距离已有的初始聚类中心最远的样本作为第2个初始聚类中心；

(5)重复执行步骤(4)直到初始聚类中心中包含k个样本。

上述步骤中percent的值过大会引入噪声样本点，过小又会使得高密度样本集中样本数据过少。经过综合考虑，文中设置percent为20%。这个参数并不是固定不变的，可以根据数据集的具体情况进行调整。

在高密度数据集上应用最小最大原则得到的k个初始聚类中心，既考虑到了数据的分布情况，又可以避免离群样本点的干扰。文中基于上述两点改进思想实现了改进的kmeans算法(记做Improve-Kmeans算法)，并将其应用于学生消费数据集，以更好地描述学生群体的共性与特性。

2 实验分析

2.1 实验环境与数据

文中以西安某高校2019年03月—2019年06月的17、18级硕士研究生的一卡通消费数据作为样本集，原始数据由学校信息中心提供，其格式如表1所示。

表1 一卡通消费数据集(部分)

原始的一卡通消费数据集中不仅包含所有学生的一卡通消费记录，还包含部分教职工及学校管理人员的数据，这些数据属于噪声数据，分析这些噪声数据会对挖掘结果产生一定程度的影响。因此，文中的首要工作就是从原始数据集中去除噪声数据(在校学生之外的所有其他人的消费数据)。

一卡通消费数据集中只记录着每一次消费的记录，对单一记录进行分析无法得出有用的结论，只有根据具体需求构建合适的特征后才能应用于聚类算法中，使数据挖掘更有针对性，从而提高算法性能。

为了全面刻画学生的特点，文中从多个角度分层提取了学生消费特征。表2展示了这些特征的基本信息。

表2 学生消费特征

2.2 实验方法

为了确定Improve-Kmeans算法中k的取值，通过对处理后的学生消费数据集进行k=1到8的聚类实验，得到k在不同取值下聚类结果的误差平方和(sum of the squared errors，SSE)，具体步骤如下：

(1)设k=1，运行Improve-Kmeans算法；

(2)记录k=1下得到的各个聚类中心及样本所属的类别；

(3)按照公式(2)计算组内方差SSE，并记录；

(4)设k=2到8，重复执行步骤(1)～步骤(3)。

(2)

式中，ci是聚类结果中的第i个类，p是ci中的样本点，mi是ci的聚类中心(即ci中所有样本的均值)。

实验结果如图1所示。

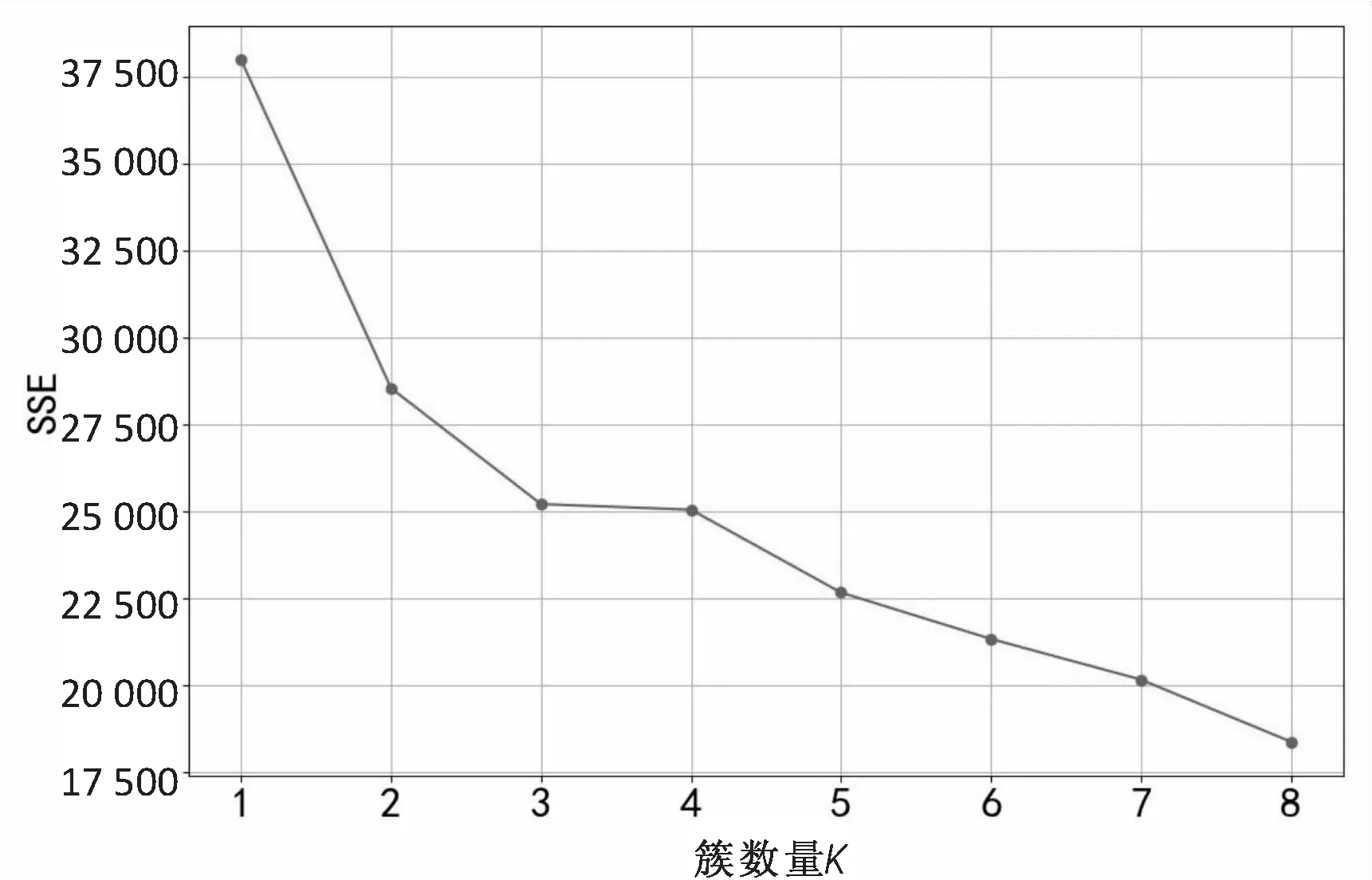
图1 不同k值下聚类结果的SSE

从图1中可以看到，随着k值的增大，SSE逐渐减小，且在k=3时SSE的减小幅度开始减缓，这表明最佳聚类数为3。

为了减少实验误差，文中运行Improve-Kmeans算法16次，每次聚类得到的SSE和轮廓系数见表3。从表中可以看出，在第11次实验时，SSE值最小且轮廓系数最大，因此文中选择该次实验结果得到的学生群体画像进行分析。

表3 16次实验的SSE和轮廓系数

文中设计了两个实验：

(1)使用Improve-Kmeans算法对学生刻画群体消费画像，并对画像进行解释分析，应用画像的结果为学校管理人员提供决策支持；

(2)将Improve-Kmeans算法得到的贫困生数据与学校线下认定的贫困生数据进行对比分析，以辅助高校精准资助活动。

2.3 学生群体消费画像

文中从三个角度：(1)3个类的聚类中心点；(2)3类学生对应的原始数据的平均值；(3)3类学生对应的原始数据的分布情况，分析学生群体的消费特征。

表4列出了第I、II、III类学生群体的聚类中心点，图2描述了3类学生群体对应的原始数据的平均值，图3描述了3类学生群体对应的原始数据的分布情况。

表4 学生群体聚类中心

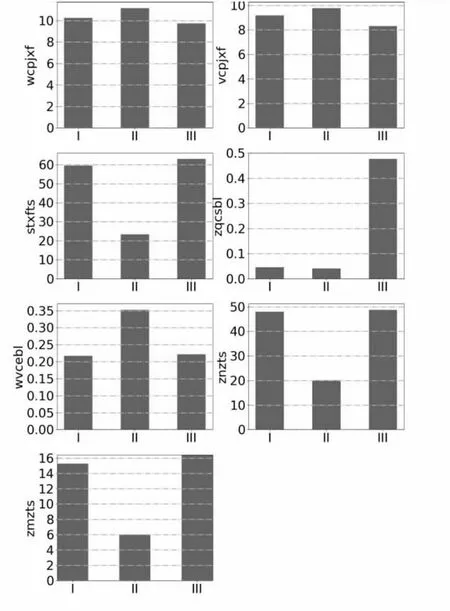
图2 3类学生的原始消费数据的平均值

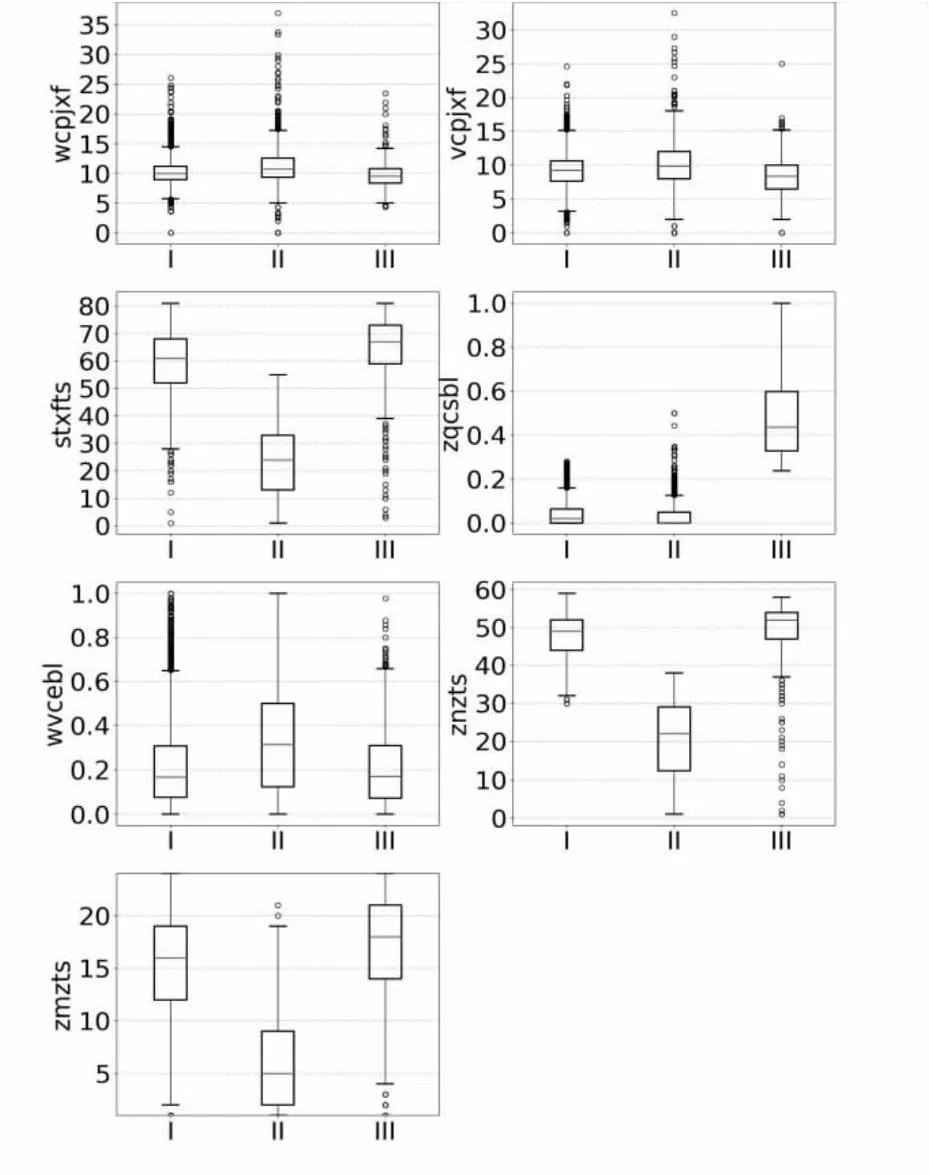
图3 3类学生的原始消费数据的分布

从图2中可以看出，对于第I类群体，其午餐平均消费、晚餐平均消费明显比第III类群体低，同时比第II类群体高，说明其消费水平在三类群体中居中。其食堂消费天数接近第III类群体且明显高于第II类群体，说明这类学生频繁在食堂就餐。其午晚餐差额比例明显低于第II类群体，说明这类学生的饮食比较规律。周内在校天数和周末在校天数接近第III类群体且明显高于第II类群体，说明这类学生经常在校。早起次数比例接近第II类群体且明显低于第II类群体，说明这类学生同样很少早起，属于懒癌患者。综上分析，第I类学生符合大部分正常学生的消费情况。

对于第II类群体，其午餐平均消费、晚餐平均消费明显比第I和III类群体高，说明其消费水平是三类群体中最高的。其食堂消费天数最低且明显低于其他两类群体，说明这类学生很少在食堂吃饭。其午晚餐差额比例最高且明显高于其他两类群体，说明这类学生经常性的只吃单餐，饮食不规律，很可能是经常点外卖。周内在校天数和周末在校天数最低且明显低于其他两类学生，说明这类学生喜欢经常离校。早起次数比例最低，且明显低于第III类群体，说明这类学生很少早起。综上分析，第II类学生符合小富群体的行为特点。

对于第III类群体，其午餐平均消费、晚餐平均消费最低且明显比第I和II类群体低，说明其消费水平是三类群体中最低的。其食堂消费天数最高且明显高于其他两类群体，说明这类学生是最频繁在食堂就餐的学生。其午晚餐差额比例接近第I类群体且明显低于第II类群体，说明这类学生的饮食比较规律，午晚餐消费次数基本上相同。周内在校天数和周末在校天数最高且明显高于第II类群体，说明这类学生是最常在校的学生。早起次数比例最高且明显高于其他两类群体，说明这类学生拥有早起的好习惯。综上分析，第III类学生符合贫困生群体的行为特点。

表4中的“所属类包含的样本数量”列的结果也能验证学生群体分类结果。第III类贫困生群体共415人，占总人数的7.64%，符合该校研究生中的贫困生数量和比例，第I类普通学生群体共4 133人，占总人数的76.16%，基本上也符合现实情况。

图3是3类学生群体在消费特征上对应数据的箱型图，横坐标代表学生群体，纵坐标代表各类群体在各特征上原始数据的分布情况，文中以第III类群体为例分析此类群体的消费特点。从图中可以看出第III类群体在特征：午餐消费金额、晚餐消费金额、食堂消费天数、午晚餐差额比例、周内在校天数、周末在校天数上的四分位距明显比第II类群体小，说明第III类群体在这些特征上数据的分布比较集中，波动范围小，消费习惯比较规律。

在特征：午餐消费金额，晚餐消费金额，午晚餐差额比例上的最大值、最小值、中位数、上下限比第I和第II类群体小，说明这类群体的消费水平较低。在特征：食堂消费天数，周内在校天数，周末在校天数的最大值、最小值、中位数、上下限明显比第I和第II类群体大，说明这类群体是最经常在校内就餐、很少离校。在早起次数比例上的各特征明显高于其他两类群体，说明这些学生喜欢早起，有着良好的习惯。综上，第III类群体可以认定是有着良好生活和消费习惯、基本上不离校且消费水平较低的贫困生。各个群体消费数据波动程度的分析结果和上面各个群体聚类中心的分析结果相同。

2.4 聚类标记的贫困生分析

为了验证Improve-Kmeans算法标记贫困生的效果，文中获取了学校线下认定的2017级和2018级的贫困生名单，共349人。聚类标记与线下认定的贫困生名单重合率为47%，分析原因可能有两方面：(1)Improve-Kmeans算法还需要进一步完善以更好地适应高校贫困生认定的应用环境；(2)线下贫困认定名单具有很大的不确定性，老师、学生很多情况下是通过申请表、平时的认知(甚至并不认识)来进行贫困认定，可能存在误判的情况。因此文中以午餐平均消费水平和食堂就餐天数两个特征为例，研究两种方法中不重合的学生的消费情况：分别统计仅在聚类标记名单中出现的贫困生和仅在线下认定名单中出现的贫困生的午餐平均消费水平和食堂就餐天数，并绘制对应的概率密度曲线，如图4所示。

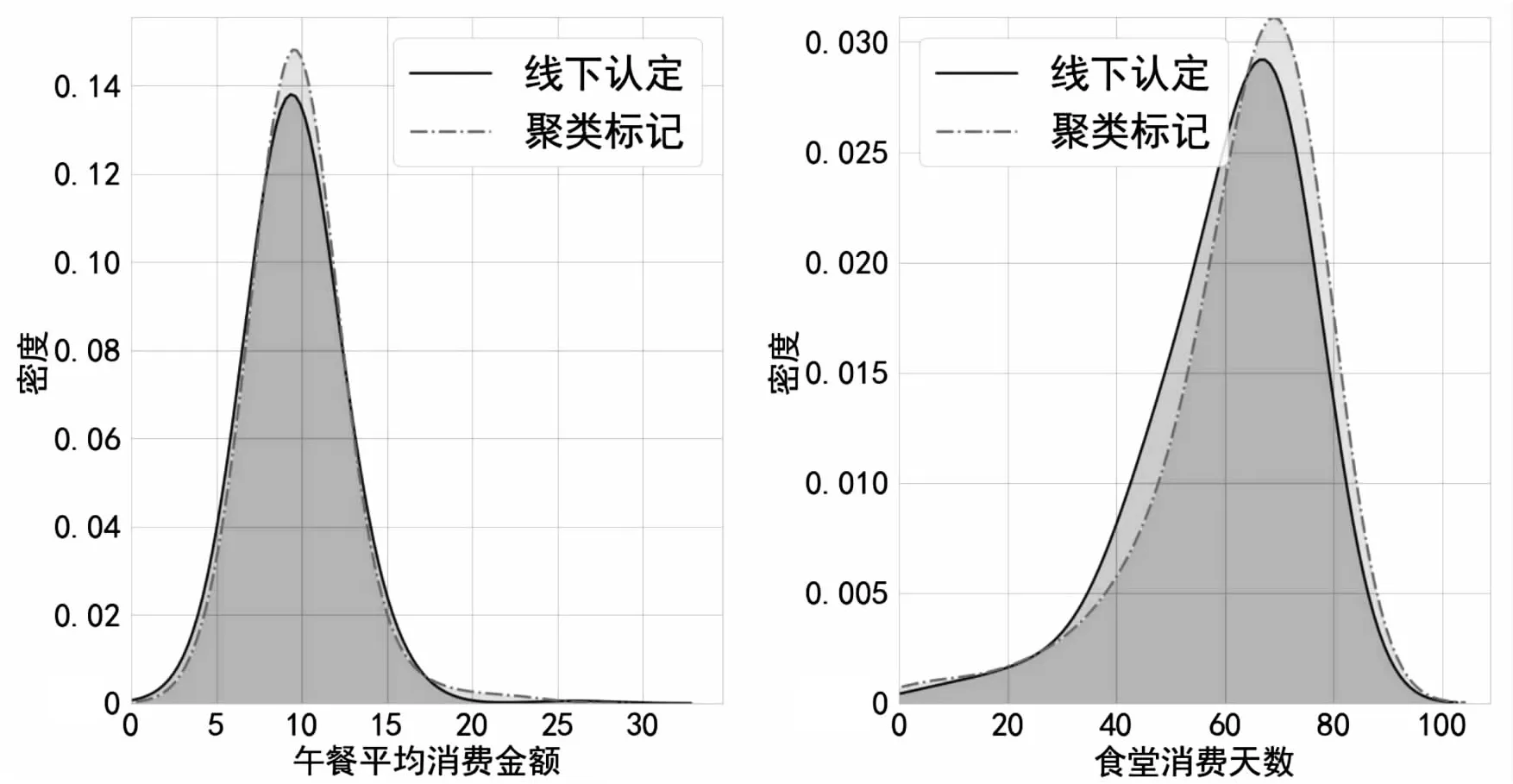
(a)午餐平均消费金额概率密度曲线 (b)食堂消费天数概率密度曲线图4 消费水平的概率密度曲线

从图4(a)中可以看出，聚类标记贫困生的密度曲线比线下认定贫困生的密度曲线更加集中，这意味着聚类标记的贫困生比学生认定的贫困生的午餐平均消费金额波动更小，更加稳定。

从图4(b)中可以看出，聚类标记贫困生的密度曲线所处的位置明显比线下认定贫困生的密度曲线所处的位置整体偏右，这意味着聚类标记的贫困生更偏向于在食堂就餐。

从午餐平均消费和食堂消费天数两个指标上可以看出，相比没有加入数据挖掘算法的线下贫困认定而言，基于客观消费数据聚类挖掘贫困生的方法更加适用。

聚类标记贫困生方法和线下认定贫困生方法的总结如下：

(1)聚类标记贫困生的目标是找出消费水平低的贫困生，不考虑任何人为因素，单纯从客观的学生消费数据出发，挖掘各个群体的学生的消费水平，找出消费水平较低的贫困生。但是没有考虑到学生家庭条件、健康情况、家庭人口情况和是否低保户等信息；

(2)线下贫困生认定的目标是找出家庭经济情况困难的贫困生，以学生家庭收入情况、健康情况、家庭人口情况和是否低保户等信息为标准，按照流程进行贫困生认定。但是没有考虑学生的消费数据，难以发现没有申请贫困认定的隐藏贫困生和申请了贫困认定的伪贫困生。

具体的贫困生认定工作可以结合这两种方式的优点：对于聚类标记认定的贫困生(或只考虑客观消费数据的挖掘算法挖掘出的贫困生)可以发放专项的贫困生助学基金；对于线下流程化认定的贫困生可以按照国家的要求发放贫困生补贴。

文中算法不仅可以用来辅助贫困生的认定，还为以后更深入地利用数据挖掘相关技术研究高校精准资助活动提供了支持，值得进一步研究。

3 结束语

为了全面了解学生的行为特点，文中从学生群体的角度出发，利用学生校园消费数据研究不同学生群体行为特征的相似性与差异性。采用适合校园消费数据场景的Improve-Kmeans聚类算法对研究生的消费数据集进行聚类，分析不同学生群体的消费特征，进行画像说明。同时对比分析了聚类得到的贫困生的消费数据和线下认定的贫困生的消费数据，为贫困生认定工作提出了改进意见，为高校的精准资助工作提供数据支持，为学生的校园学习生活保驾护航。