文件分层-属性基多关键字可搜索加密方案

蒋 英，陈燕俐，高诗尧

(南京邮电大学 计算机学院、软件学院、网络空间安全学院，江苏 南京 210003)

0 引 言

近年来，云技术得到了飞速发展，已成为计算机科学中的重要领域。云技术不仅提供计算服务，还提供存储服务，可以使用户受益于解决数据共享的爆炸性增长问题。文件属主(data owner，DO)的文件可以存储在多个服务器上，并由其他数据用户共享。为了确保存储在远程服务器上的文件不会被其他数据用户或恶意服务器破坏，DO通常会在数据上传到云端之前对数据进行加密，但是加密可能会导致用户(data user，DU)无法对密文进行搜索，在某种程度上限制了文件搜索的灵活性。为了解决搜索加密文件的问题，专家们提出了可搜索加密(search encryption，SE)技术，DO对共享数据和文件和关键词进行加密，并上传至服务器。SE可充分利用云服务器庞大的计算资源进行密文上的关键字查找，不仅保证了用户数据的安全和隐私，而且能够节省大量的网络传输和计算开销。随后，大量关于可搜索加密的文章被提出，目前SE方案根据其构造算法的不同可以分为两类：对称可搜索加密算法[1]和公钥可搜索加密算法[2]。前者的构造通常基于一些伪随机函数生成器、哈希算法等，更适用于单用户模型；后者主要使用双线性映射等，并且将安全问题建立在一些复杂性假设上，更适用于多用户体制。另外还包括单关键字布尔搜索方案[3-5]和多关键字布尔搜索方案[6-9]。但传统的一对一的可搜索加密不能适应云计算海量用户和数据的安全管理以及细粒度的关键字搜索，云场景下，加密者往往想将数据分享给一些的特定的、满足一些固定条件的人，如何做到云存储数据的细粒度的加密数据访问控制和密文检索，成为了研究者面临的一个关键挑战。2005年Sahai和Waters[10]提出了基于属性加密(attributed-based encryption，ABE)机制，通过引入了属性集合和访问策略的概念，将一系列的属性集合看作用户的身份标识，当属性和访问结构相匹配时，才能解密密文。2013年，Kulvaibhavh等人[11]首先提出了基于属性的可搜索加密方案(attribute-based search encryption，ABSE)，将灵活、高效和细粒度的ABE加密机制和可搜索加密技术相结合，实现了云环境安全、高效、细粒度的数据共享以及密文检索。

考虑到在多数云计算实际应用环境中，共享的多个文件通常具有层次结构。以个人健康记录(personal health records，PHR)为例[12]，为了在云环境中安全地共享PHR信息，患者将其PHR信息M分为两个部分：个人信息文件m1和病例信息文件m2。患者根据实际需要，会通过不同的访问策略对文件m1和m2进行加密。设患者将m1的访问结构设置为P1：{(心脏病学AND研究员)AND主治医师},m2的访问结构被设置为P2： {心脏病学AND研究员}。显然，如果分别使用访问结构P1和P2对m1和m2进行加密，文件需要进行两次加密，部分密文会出现重复。考虑到通常情况下，当用户可以解密m1时，他必然可以解密m2，Wang等人首次提出了文件分层-属性加密方案(file hierarchy attribute-based encryption，FH-ABE)[13]，通过引入层节点和传输节点等概念，将多个访问策略集成为一个访问结构，缩短了密文长度，同时用户可以解密当层以及以下层的所有文件，从而提高了解密效率。为了实现分层文件上的可搜索加密，Miao等人[5]将FH-ABE方案与SE方案相结合，提出了文件分层的基于属性的可搜索加密(file hierarchy attribute-based searchable encryption，FH-ABSE)等方案。然而，目前的FH-ABE和FH-ABSE方案只支持树形访问结构，解密运算由于采用递归和拉格朗日差值计算，计算效率低，并且需要逐层计算节点的信息，解密开销较大。同时目前的FH-ABSE方案还存在以下两个问题：(1)采用先解密，再进行关键字匹配的方式，造成关键字搜索效率较低；(2)索引密文与关键字个数相关，当关键字较多时，存储开销和计算开销较高。针对以上问题，文中以Wang等人的方案[13]为基础，构造了一个灵活的、高效的、支持LSSS访问结构的多关键字可搜索方案(file hierarchy-LSSS-attribute based multi-keyword search encryption，FH-LABMKSE)。创新点具体如下：

(1)实现了支持LSSS结构的文件分层-基于属性的加密。文中支持LSSS结构，通过将秘密因子逐步分配的方法，巧妙地避开了采用访问树结构方案在解密时的递归和拉格朗日差值计算。另外将下一层的密文信息直接嵌入上一层的密文中，实现了密文的跳跃式传递。同时，也实现了灵活的细粒度访问控制。

(2)实现了固定索引密文长度的多关键字可搜索。本方案关键字索引大小与计算开销都与关键字个数无关，和目前的多关键字可搜索方案中关键字密文大小和计算开销随着关键字个数线性增长相比，在固定了关键字密文长度的同时，还提高了计算效率。另外本方案采用先关键字匹配，然后符合访问结构的用户再解密的方式，和目前先解密再关键字匹配的方案相比，提高了关键字的搜索效率。

(3)不仅关键字搜索功能是由云服务器完成的，并且将解密的一部分计算任务转移到云服务器，从而降低了用户的计算负担，而云服务器在整个过程中不会得到和关键字有关的有用信息。

1 相关工作

1.1 分层的基于属性的加密

为了在加密文件上实现分层的细粒度访问结构，Wang等人首次提出了一个分层CP-ABE方案[14]。随后，出现了一系列具有特殊功能的分层CP-ABE方案[15-16]。但是，它们仅仅考虑了属性的分层，却没有考虑文件的分层。为了支持对分层文件的访问控制，Wang等人[13]提出了FH-CP-ABE方案，通过将多个访问树集成为一个访问树，用户可以通过计算一次解密密钥来解密多个文件，既节省了密文存储空间又节省了加解密时间。并且，当系统的文件越多，方案的效率越高。2019年，Fu等人[17]提出了实用的密文策略-基于属性的文件分层加密方案。该方案首先根据文件的属性构造了一组相互独立的访问树，其次采用贪婪策略来构建合并这些树，然后通过合并各个小树来动态生长树。将集成访问树中的所有文件加密在一起，提高了加解密的效率。

1.2 基于属性的可搜索加密

2013年，Wang等人[18]结合CP-ABE和公钥可搜索技术，提出基于属性的可搜索加密方案。2017年，Gowda等[19]提出了文件分层的可搜索加密方案，该算法具有定时启用的隐私保护关键字搜索机制。提出的方案允许数据用户基于属性集在数据拥有者提供的持续时间内执行关键字搜索。它支持在数据拥有者提供的指定时间后自动撤销访问权限。它保证了机密性，同时保持了细粒度的访问控制和通用的客户端撤销。Miao等人提出文件分层的属性可搜索方案[5]支持细粒度的单关键字搜索和细粒度的多关键字搜索。但是，目前多关键字可搜索方案仅支持访问树结构，并且密文多数都是随着关键字的增加而线性增长，当关键字较多时，存储开销较大。

2 预备知识

定义1 双线性映射[10]。设置两个阶为素数p的乘法循环群G0和GT，g是G0的一个生成元。存在一个双线性映射e:G0×G0→GT，必须满足以下3个条件：

(a)双线性。对任意u,v∈G0，任意a,b∈Zp,都有e(ua,vb)=e(u,v)ab。

(b)非退化性。存在u,v∈G0,满足e(u,v)≠1。

(c)可计算性。对任意u,v∈G0,e(u,v)可有效计算。

定义2 线性秘密共享矩阵(LSSS)[20]。令{P1,P2,…,Pn}为n个参与者的集合，这一组参与者上的秘密共享方案π是线性的，如果：

(a)各方的秘密因子构成了Zp上的向量。

(b)存在一个l行n列的矩阵M，称为π的共享生成矩阵。对于所有i=1,2,…,l，M的第i行为Mi，令函数ρ将参与者所在的行i定义为ρ(i)。考虑列向量v=(s,r2,…,rn)，其中s∈Zp是要共享的秘密值，r2,…,rn∈Zp是随机选择的，则M·v是l个秘密因子的向量。每个秘密因子λi=Mi·v属于参与者ρ(i)。

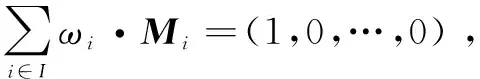
3 FH-LABMKSE方案的安全模型

本方案的安全模型与原始的LSSS-CP-ABE方案[20]相同。文中在敌手A和挑战者B之间定义CPA(chosen plaintext attacks)安全游戏，如下所示。

系统建立。B运行FH-LABMKSE的Setup阶段，输出公开参数PK，并将PK发送给A。

询问阶段1。A重复地对属性集S1,S2,…,Sq1进行私钥查询。

挑战。A选择两个要受到挑战的等长的信息m0和m1。同时，A给定一个受到挑战的访问结构A*使得没有任何询问阶段1的集合Si满足A*。B选择一条信息mρ,ρ∈{0,1}，并且用Α*加密。B将密文CT*返回给A。

询问阶段2。A重复询问阶段1的步骤，但是，属性集Sq1+1,…,Sq都不满足与挑战相对应的访问结构。

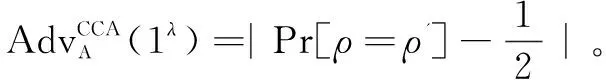
定义4 如果没有敌手能够在多项式时间内以不可忽略的优势赢得上述安全游戏，则FH-LABMKSE方案是CPA安全的。

4 FH-LABMKSE方案

4.1 系统模型

设关键字集W={w1,w2,…,wm}，DO首先从文件集F={F1,F2,…,Fk}中提取关键字，并为每个文件构造关键字索引向量Di={di,1,di,2,…,di,m}(若di,θ为1,表示Fi中有第θ个关键字,否则为0)。接着，DO利用不同的对称密钥cki分别加密文件Fi，并加密对称密钥集ck={ck1,ck2,…,ckk}和关键字索引向量。当DU想要访问包含其预计关键字的密文时，必须将根据查询的关键字生成的陷门传送给云服务提供商(cloud server provider，CSP)。此后，当且仅当其陷门与访问结构匹配时，CSP才会返回相关的密文。

系统模型如图1所示，文中系统主要涉及四种不同类型的实体：文件属主(DO)、用户(DU)、云服务提供商(CSP)和授权中心(attribute authority，AA)。假设DO拥有k个文件，并且文件集F={F1,F2,…,Fk}在云存储中共享。AA是一个完全受信任的实体，并且接受云储存中的用户注册，为用户生成属性私钥。CSP是一个半可信的实体。CSP会好奇存储在云上的数据，但是绝对忠诚，会严格履行特定的服务，不会恶意删除数据或者拒绝响应用户的请求。在本系统它提供密文存储、关键字检索和部分解密工作。

图1 系统模型

4.2 FH-LABMKSE方案具体构造

(a)初始化算法Setup。

由AA执行，输入安全参数λ。生成阶为素数p的乘法循环群G、GT。给定双线性映射e:G×G→GT,g为G的生成元。设系统中属性集合U，系统属性个数为|U|。随机生成群元素hattr(1),…,hattr(|U|)∈G。AA定义两个哈希函数H:{0,1}*→G，H1:{0,1}*→Zp。最后，随机选择α,a,b∈Zp，生成PK和MSK，PK发布在AA的公共布告板上，MSK自行秘密保存。

PK={e(g,g)α,g,ga,gb,hattr(1),…,hattr(U),H,H1}

(1)

MSK={gα,b}

(2)

(b)用户密钥生成算法Kengen。

由AA执行，当用户加入时，根据用户属性集S，AA选择一个随机值t∈Zp，生成DU的属性密钥SK，并传送给用户。

(3)

(c)索引密钥生成算法TKengen。

用户随机选择z∈Zp，生成一对索引公私钥对，TPK=e(g,g)z为索引公钥，TSK=z为索引私钥。

(d)关键字和文件加密算法Encrypt。

由DO执行，假设文件集F={F1,F2,…,Fk}，对称密钥集ck={ck1,ck2,…,ckk}分别用来加密k个文件，文件等级由1到k递减。

DO采用一个分层的访问结构加密k个对称密钥。在分层访问结构中，每一层只加密一个对称密钥。分层的访问结构实际上是多个访问策略的聚类，它包含很多个访问策略，每个访问策略对应一个对称密钥。这些访问策略存在从属关系，即Pk⊂Pk-1⊂…⊂P1。若DU能够解密Pi，那它必然可以解密Pi+1,i∈[1,k-1]。DO根据P1，生成一个访问矩阵(M,ρ)，M是l×n的矩阵，l是P1中的属性个数。选择一个向量v={s1,y2,…,yn}∈Zp，s1是加密ck1的秘密因子。DO通过计算v×Mi得到每个属性对应的秘密因子λi，其中Mi是矩阵M的第i行向量。根据文献[21]中的访问矩阵构成方式，不难看出，或门的孩子节点的秘密因子等于该或门节点的秘密因子，而无论一个与门节点有多少孩子节点，它的秘密因子都等于它的左孩子节点的秘密因子减去右边所有孩子节点秘密因子的和。因此当DO得到每个属性的秘密因子和s1后，便可自上而下地重构每个子访问策略Pi的秘密值si,i∈[2,k]。

图2 分层访问结构中秘密因子的分配

为P1随机选择一个秘密值s1=2，接着选择两个随机数，设y2=1，y3=-3，构成向量v=(2,1,-3)，图2给出了各节点分配的秘密因子，可知P2的秘密值为3。

DO随机选择r1,r2,…,rl∈Zp，生成文件密文和关键字密文的步骤如下：

•文件密文的生成。

用对称密钥cki加密每个文件Fi，得到数据密文CFi=Enc(Fi,cki)(此处Enc是一种对称加密算法)。

再用文件分层的属性加密机制对cki进行加密，生成密文如下：

(4)

Λi=e(g,g)α(si+si+1)·H(e(g,g)αsi)

i∈[1,k-1]

(5)

(6)

•关键字密文的生成。

DO根据每个文件的关键字索引向量Di={di,1,di,2,…,di,m}以及自己的索引私钥z，为每个文件Fi生成关键字密文I={Ii}:

(7)

最后，DO将密文CT={C,I}上传到CSP。

(e)陷门生成算法Trapgen。

DU执行该算法。W'为DU的查询关键字集。DU首先向DO申请获得索引公钥e(g,g)z,再根据W'生成查询向量Q={q1,q2,…,qm}，若关键字wθ在W'中，那么qθ为1，否则为0。DU随机选择v∈Zp，生成陷门T。

•DU生成与密钥相关的陷门组件T1：

(8)

•DU生成与关键字相关的陷门组件T2：

(9)

最后DU将完整的陷门T={T1,T2}发送给CSP。

(f)搜索算法Search。

•CSP首先验证e(I,t1)≥t2是否成立：

(10)

(11)

(g)解密算法。

Decrypt(CT',SK):DU根据CT'和SK计算：

(12)

基于分层的特性，DU也能够解密位于i层以下的密文：

(13)

最后获得相应的对称密钥：

(14)

从而解密CFi获得文件集F。

4.3 安全性证明

定理1：如果q-parallel-BDHE假设成立，那么攻击者不可能在多项式时间内找到一个不可忽略的概率以大小为l*×n*的挑战矩阵，选择性地攻破文中方案，其中l*、n*≤q，即提出的方案在随机预言模型下是选择性CPA安全的。

证明：假定在选择安全性的情况下有多项式时间敌手A可以有不可忽略的优势攻破本方案，那么敌手A可以构建出一个挑战者B以不可忽略的优势解决q-parallel BDHE的问题。具体过程如下：

(a)初始化。

挑战者B接受q-parallel-BDHE挑战向量y和随机数T。A选择挑战访问策略(M*,ρ*)，M*有n*列，并将其发送给挑战者B。

(b)系统建立。

(c)阶段1。

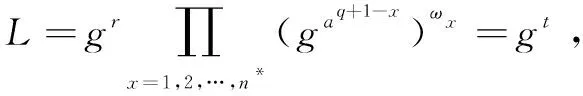
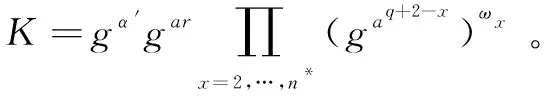
(d)挑战。

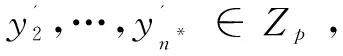
(e)阶段2。

与阶段1相同。

(f)猜测。

5 性能分析

文中方案与Miao的两个方案[5,8]进行了存储、通信开销和计算开销的比较。方案[8]实现了树形访问结构的基于属性的多关键字可搜索加密，方案[5]实现了树形访问结构的、文件分层-基于属性的多关键可搜索加密。在文献[5]中，密文信息的传递是由传输节点进行的。文献[5]中对传输节点的定义为：如果一个节点的孩子中至少有一个包含门限值，那么就称它为传输节点。

令LG,LGT分别表示G、GT中元素的长度，|Ale|，|Ant|分别表示访问结构中属性的数量和传输节点的数量。令|S|表示用户的属性数量，U表示系统中属性的个数。m表示关键字的个数。表1比较了3种方案公开参数大小、主密钥大小、用户属性密钥大小、索引密文大小以及陷门大小。从表中可以看出，文中方案的关键字索引密文长度小于方案[5]和方案[8]的。这是由于本方案的关键字索引密文与关键字的个数无关，是固定长度的，而另外两个方案都随着关键字数量的增加线性增长。

表1 与不同方案的存储、通信开销的比较

表2 与不同方案的计算开销的比较

对计算开销的比较，为了方便，本节主要考虑了耗时的指数运算和双线对运算，令EG、EGT表示群G、GT的指数运算时间；e表示双线性配对计算时间。表2给出了在k个文件、m个关键字的条件下三种方案的Kengen算法、Encrypt算法、Trapgen算法和Search算法的计算开销。j表示每个传输节点的子节点数。从表2中可以看出，文中方案的加密时间随k线性增长，另外两个方案均随km线性增加。同时，因为文中取消了传输节点，因此加密计算开销明显低于其余两个方案。

6 结束语

文中实现了一种文件分层的多关键字可搜索方案，在云环境中实现了安全灵活的文件分层的细粒度访问控制和关键字搜索。方案通过将秘密值分配的方法，将下一层的秘密值直接嵌入上一层的密文中，提高了分层文件的解密效率；其次通过对多关键字构造索引向量的方式，实现了固定关键字密文长度的多关键字可搜索，最后采用先关键字搜索，再解密的方式进一步提高了关键字的搜索效率。该方案不仅提高了解密效率，而且节省了通信和存储开销。