“简单多面体外接球”微专题教学课例有感

文/广州市番禺区石北中学 孙文志

课程标准对直观想象的内涵、价值、主要表现以及水平划分等作了详细的表述。课程标准指出，直观想象是指借助几何直观和空间想象感知事物的形态与变化，利用空间形式特别是图形，理解和解决数学问题的素养。主要包括：借助空间形式认识事物的位置关系、形态变化与运动规律；利用图形描述、分析数学问题；建立形与数的联系，构建数学问题的直观模型，探索解决问题的思路。直观想象教学的优点：对于数学教学，直观想象能够促进学生对客观事物的正确认识，几何知识的教学活动是对学生直观想象训练的最佳载体。同时，直观想象的教学主要体现在几何知识的讲解中，通过促进学生的思维，来实现最有效的教学。直观想象能够作为其中的核心概念之一，充分凸显出在让学生全面发展、落实立德树人根本目标等方面的重要性。

在讲解关于简单多面体外接球时，以往通常都是一个很简单教具模型，无法应对大部分球体实际直观图，学生大多记住公式求解。新课标中核心素养的提出充分肯定了我们“不是为了考试而教学，而是为了培养人而教学”。笔者尝试利用Cabri 3D 辅助立体几何教学制作动态几何体，通过动态进行探究，让学生能看到了模拟的几何体直观图，通过直观感知，发现并理解公式定理，培养了学生的创新思维，进一步激发了学生的直观想象能力。

一、内容分析

本专题是选自高三“简单多面体的外接球”的微专题复习课，主要从最基础的球心与截面外接圆连线垂直于截面公式：R2=r2+d2，推广到正棱锥的外接球问题，侧棱与底面垂直的简单多面体，两方面由浅入深复习。重视公式的形成过程，利用Cabri 3D 软件制作简单多面体外接球模型，把直观图全方位呈现给学生，让学生能积极参与学习过程，直观观察推理公式的由来，更好的理解公式的用法，有意识去培养学生数学直观想象能力与逻辑推理能力。

二、学情分析

本班的学生是历史+政治+生物班，学生的基础属于中等或偏下，女生较多，学生对立体几何一直比较抗拒，空间想象力较弱，复习课好像是在讲新课。此节课已经复习完立体几何直线与平面，平面与平面关系，基本具备证明直线与平面垂直，平面与平面垂直的证明。

三、教学目标与重点、难点

教学目标：（1）通过三种简单多面体Cabri 3D 图，观察球半径R，底面外接圆半径r，与底面垂直线段（或球心到底面外接圆圆心的连线长d）三者之间的关系；（2）在探索过程活动中，培养学生直观想象和逻辑推理能力；（3）在Cabri 3D动态图变化过程中，可以对R2=r2+d2公式进行更深层次的探究。

重点、难点：（1）重点：简单几何体外接球公式的探索及应用；（2）难点：一侧棱与底面垂直型几何体外接球的公式的应用。

四、教学过程

1.引例

A.36π B.64π C.100π D.144π

图1

探究：为什么球心O 与截面外接圆圆心O1连线OO1垂直于截面ABC？

如图2，连接A O1所在的直径交外接圆于点D，连接OA，OD，则三角形 OAD 为等腰三角形，O1是AD 中点，则OO1⊥AD，同理：OO1⊥BO1，则OO1垂直于截面 ABC。

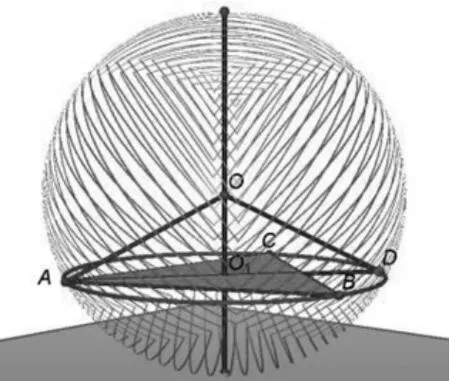
图2

公式：R2=r2+d2（球半径 R，底面外接圆半径r，球心到截面外接圆圆心连线长为d）。

练习：（2020 年高考数学全国卷理 10）已知 A，B，C 为球 O 的球面上的三个点，⊙O1为△ABC 的外接圆，若⊙O1的面积为 4π，AB=BC=AC=O O1，则球 O 的表面积为（ ）。

A.64π B.48π C.36π D.32π

2.例题

正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积为（ ）

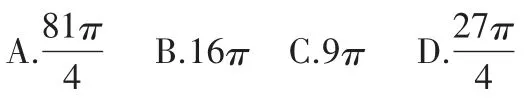
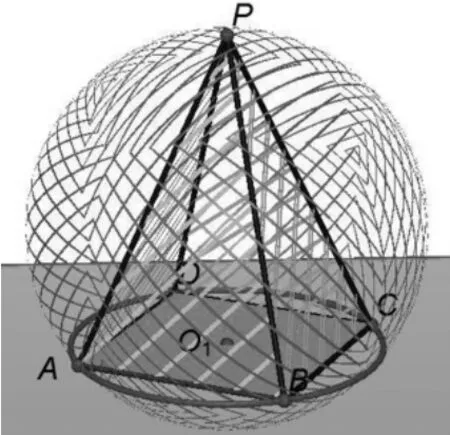
图3

如图4，正四棱锥的外接球顶点P 在底面的射影落在底面的中心O1位置（即正方形ABCD 外接圆的圆心），所以顶点 P 与底面O1的连线PO1垂直底面ABCD，则正四棱锥的高为PO1=h，而球心 O 与O1的连线OO1也垂直于底面ABCD，所以球心O 在这条高线PO1上。根据公式d=|OO1|=|h-R|，所以公式R2=r2+d2变为R2=r2+（h-R）2

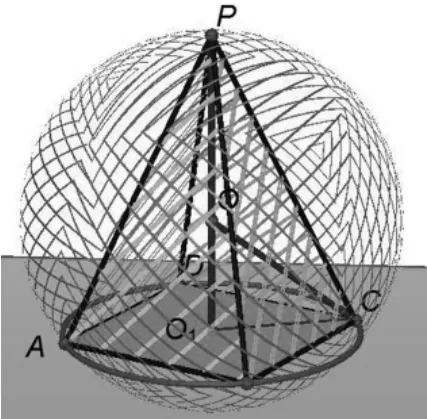
图4

对公式拓展：椎体的顶点到底面垂线的投影落在底面所在圆的外接圆圆心上时，几何体外接球的位置关系变化。

3.变式（略）

4.课后作业（略）

5.归纳总结知识升华

R2=r2+d2球半径为 R，截面外接球半径r，球心与截面圆心的连线长为d，当几何体为正棱锥时，公式变形为：R2=r2+（h-R）2，注意高有两种情况。h 为正棱锥的高。当几何体有一侧棱垂直底面时，公式变形为为侧棱长。

五、教学感悟

1.本微专题是简单几何体外接球的基础课，学生虽然之前接触过，也刚刚学习直线与平面，平面与平面关系的证明，但对于球体的认识仍是一片空白。因此，笔者从学生最熟悉的简单截面圆与球心的关系、长方体外接球入手，由浅入深、层层递进展开教学。

2.通过Cabri 3D 模拟动态立体几何图形进行探究等方式，让学生知道公式的由来，重视知识的形成过程，数形结合，加强学生对知识的理解，能发挥学生的主观能动性，培养学生的数学核心素养。

3.引导学生进行知识的深化，教师不应该把要传授的知识按部就班地向学生讲解，而应该引导学生探究，让学生“再深化”要掌握的知识，从中体悟研究方法，这才是思维真正的训练。

微专题教学实践证明，学生在遇到多面体外接球的问题时不会再像以前那样畏惧，而是慢慢体会到解题方法，找到解题的感觉。基于直观想象素养下的高中数学立体几何空间公式定理教学，不仅能够突出几何公式定理教学的重点，突破教学的难点，同时也为教师在处理教学过程中遇到的抽象问题找到突破口。采用Cabri 3D 辅助立体几何教学软件制作空间立体图形，培养直观想象素养来促进教学的开展，为教师在各环节的教学中指明了方向。