发射系下的SINS/CNS/GNSS组合导航UKF滤波算法
2021-10-27乔玉新林雪原张吉松陈祥光
乔玉新,林雪原,*,张吉松,陈祥光,2
1. 烟台南山学院,烟台 265713 2. 北京理工大学,北京 100081
1 引言
目前,组合导航系统已广泛应用于航空、航天和航海等领域,必须以特定的坐标系作为测量载体导航参数的基础。近地空间中,如机载导航系统建立在地理坐标系下,也是目前研究较多的一种情况[1]。文献[2-3]针对弹载系统的导航需求,建立基于发射惯性坐标系的SINS/CNS/GNSS组合导航模型。文献[4]针对极区范围经线变化速度加快并聚于极点的情况,建立了基于地球坐标系的SINS/GNSS组合导航模型。随着需求的增加,组合导航系统的研究广度进一步扩展。
针对基于发射惯性坐标系下的SINS/CNS/ GNSS组合导航系统,文献[2-3]将姿态四元数中的矢量误差项、位置误差、速度误差构成状态向量,进而建立EKF(扩展卡尔曼滤波)模型,然而EKF因为模型线性化展开将会导致模型不准确。为此,文献[5]将粒子滤波引入该组合导航系统,但粒子滤波算法存在复杂度高和粒子退化的缺陷。文献[6]建立该组合导航系统的UKF(无迹卡尔曼滤波)模型,其核心思想是将四元数中的矢量项、位置、速度构成状态向量,并利用CNS和GNSS提供的姿态与位置测量值直接构成量测向量。然而直接控制四元数难度较大,且有可能发散[7],该文献没有给出四元数的样本采样点、均值预测和方差预测的生成过程。
基于上述原因,本文直接将弹载系统在发射惯性坐标系下的三维姿态角、三维位置、三维速度构成状态向量,并给出了三维姿态角的样本点生成、均值预测和方差预测的生成过程,进而建立了基于发射惯性坐标系下的SINS/CNS/GNSS组合导航UKF数学模型。
2 发射系下SINS/CNS/GNSS组合导航系统数学模型
2.1 状态方程
由于导航坐标系采用的是发射惯性坐标系,捷联安装的加速度计的比力方程可以描述为[2-3]
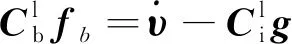
(1)

基于方程(1),位置可由速度直接积分得到

(2)
式中:p为载体在发射系中的位置;υ为载体在发射系中的速度。
采用四元数描述载体相对于发射惯性坐标系的姿态运动,避免了姿态运算过程中的奇异点,基于陀螺角速度测量值积分推算下时刻的载体姿态可表述为

(3)

由于在发射惯性坐标系中飞行器的导航工作时间均较短,陀螺与加速度计的测量误差可简化建模成“随机游走+白噪声”的形式[5],即陀螺与加速度计的实际输出ωc、fc为

(4)
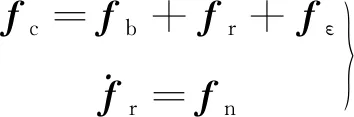
(5)
式中:fb、ωb分别为加速度计、陀螺输出的真值;fr、ωr分别为加速度计、陀螺随机游走误差;fn、ωn分别为加速度计、陀螺随机游走驱动噪声;fε、ωε分别为加速度计、陀螺测量噪声,可看作白噪声。
对四元数方程(3)求解,可得[8-9]
qk=e0.5[Δθ]qk-1=[λ0λ1λ2λ3]T
(6)
式中:λ0为四元数的标量部分,λ1、λ2、λ3为四元数的矢量分量;[Δθ]可表示为
由方程(6)及姿态方向余弦矩阵的关系,可求载体相对于发射惯性坐标系的姿态角:γ(横滚角)、θ(俯仰角)、φ(航向角)。
设a=[γθφ]T,根据方程(1)(2)(4)(5)及姿态角构成系统的状态向量:
2.2 量测方程的建立
由于GNSS位置测量值pe一般描述在地球固连坐标系中,经过如下变换可得到在发射惯性坐标系中的位置测量值Z1:
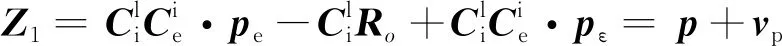
(7)
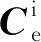


(8)

对式(8)进行姿态解算,即可获得由CNS测量的本体坐标系相对于发射惯性坐标系的姿态角Z2:
Z2=a+va
(9)
式中:va为姿态测量噪声向量。
结合方程(7)(9),则有如下的量测方程:

(10)
式中:H=[I6×606×9];V为量测噪声向量。
3 组合导航系统的UKF设计
将系统噪声W、量测噪声V与状态向量组成增广向量Xa:

(11)
式中:Pa为Xa的方差阵。
3.1 UKF算法步骤
(1)步骤1:初始化
(2)步骤2:采样点计算
i=1,…,n
(12)
i=n+1,…,2n
(13)
式中:n为Xa的维数;λ=α2(n+κ)-n,α、β和κ均为比例因子。
(3)步骤3:状态均值和方差的一步预测
以式(12)(13)所描述的采样点为初值,基于陀螺、加速度计的原始测量数据,由SINS递推计算得到k时刻的位置、速度和姿态进而构成系统状态Xi,k/k-1,i=0,1,…,2n,则

(14)

(15)
(4)步骤4:量测更新
Zi,k/k-1=HXi,k/k-1+V,i=0,1,…,2n
定义:

(16)

(17)
则
Kk=Pxz(Pzz)-1
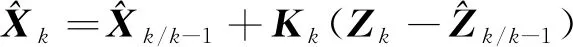
(18)
3.2 姿态采样点及统计量的计算[10-11]
第2.1小节步骤3中,位置、速度及惯性测量器件(IMU)噪声的采样点可以通过式(12)(13)线性叠加到各自均值的方式得到。而姿态角的计算是典型的非线性计算,SINS中姿态角的计算必须通过四元数与姿态矩阵得到以避免奇异值的发生,为此姿态角采样点也必须通过四元数与姿态矩阵得到,并进一步计算其均值和方差。

其中:s和c分别代表正弦和余弦函数。由方向余弦矩阵的特性,可得姿态角各采样点所对应的方向余弦矩阵:

(19)
根据式(19),求得分布于a0=[γ0θ0φ0]T周边的另外2n个姿态采样点。

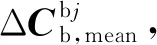

4 仿真试验与分析
为了验证本文算法的性能,设计了一条导航飞行轨迹,如图1所示。

图1 飞行轨迹Fig.1 Flight path
仿真环境为Matlab7.01,发射原点设定为(118°(E),32°(N),100 m),发射初始方位角为30°,发射时刻设定为2020-03-23T02-03-00,仿真时长为900 s。捷联解算周期设定为0.02 s,滤波周期为1 s[2-3, 5-6]。陀螺随机游走驱动噪声及陀螺白噪声均设定为0.01 (°)/s,加速度计随机游走驱动噪声及加速度计白噪声均设定为0.000 1g(g=9.8 m/s2);GNSS定位误差设定为10 m,CNS测姿误差设定为20"。
对于相同的IMU、GNSS和CNS原始数据,分别应用UKF算法及EKF算法[2-3]对数据进行处理,得到位置误差曲线、速度误差曲线、姿态误差曲线分别如图2~图4所示。

图2 位置误差曲线对比Fig.2 Comparison of position error curve
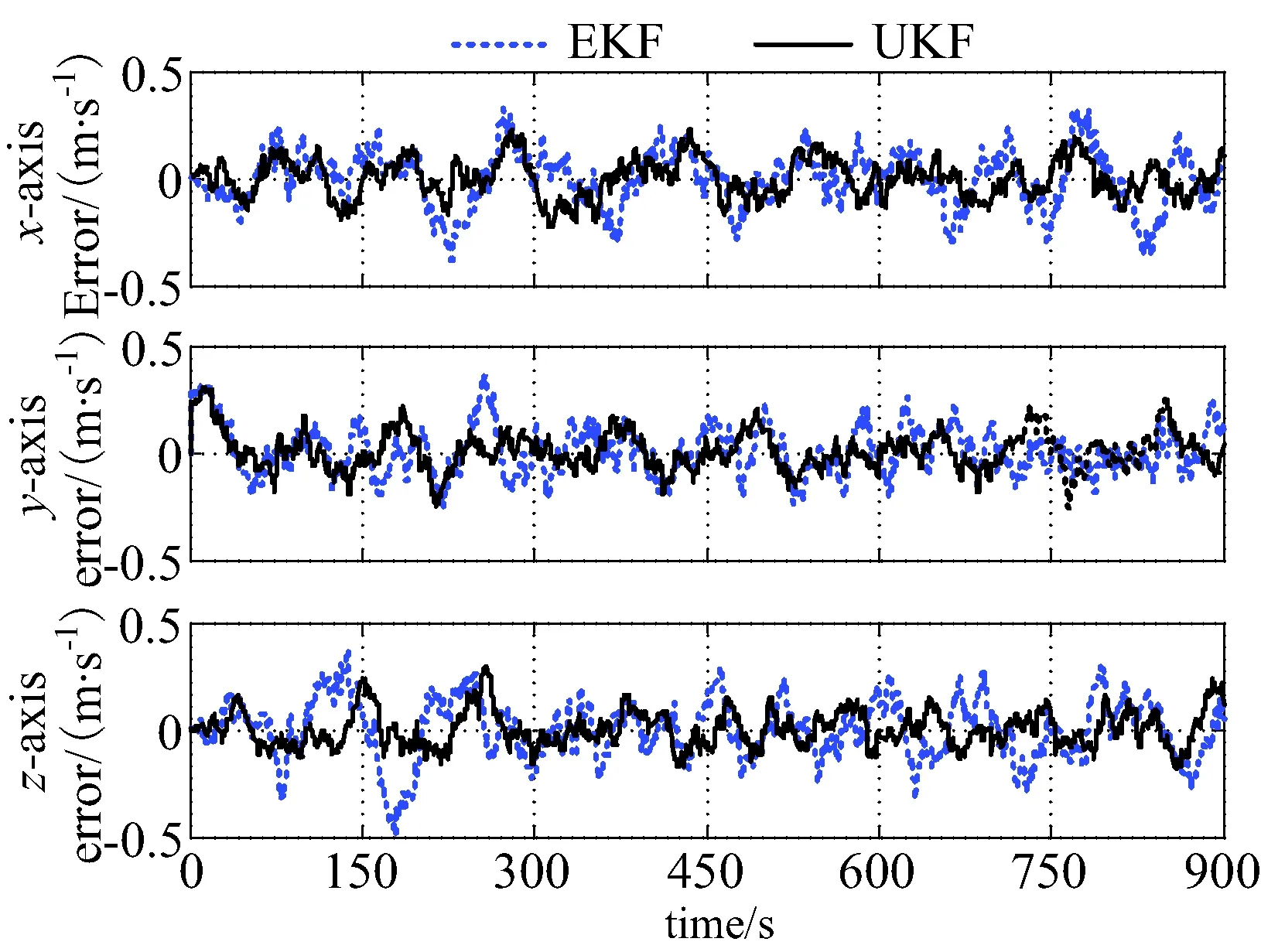
图3 速度误差曲线对比Fig.3 Comparison of velocity error curve
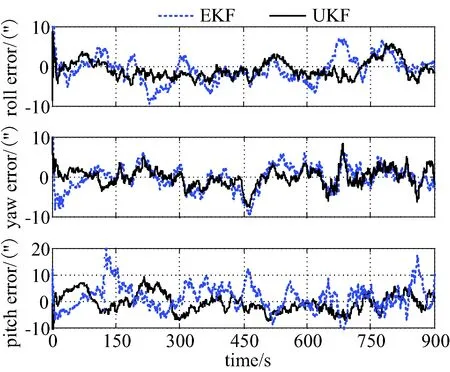
图4 姿态误差曲线对比Fig.4 Comparison of attitude error curve
根据仿真试验结果,可以获得基于UKF和EKF两种算法的各导航参数误差的统计结果如表1所示。

表1 组合导航系统EKF、UKF算法误差对比
从表1可以看出,在相同的仿真条件下,相对于EKF算法,利用UKF求得的各个导航参数所对应的误差无论是在误差最大值、误差最小值、误差均值及误差均方差方面都有较大的改善。例如对于误差均方差统计项,UKF可提高精度约20%~30%。其中的主要原因是,组合导航系统是一种典型的非线性系统,且载体处于高速、高机动状态时,UKF因为是一种非线性算法,可以避免因EFK线性化展开而引起的模型失真现象。可以说UKF的高精度特性是以较大的计算量为代价的。
为了考证UKF算法的实时性,在Intel Core i5-7200U CPU 2.70 Hz处理器环境下,在相同的原始数据条件下,UKF和EKF算法在每次滤波过程中的计算量进行对比,如图5所示。
如前所述,滤波周期为1 s,捷联解算的周期为0.02 s,由图5可以看出EKF算法每次滤波的耗时小于0.005 s(小于捷联解算周期),满足系统实时性的要求;而UKF算法每次滤波的耗时小于0.015 s(小于捷联解算周期),故UKF算法也能满足系统实时性的需求。

图5 算法计算量对比Fig.5 Comparison of algorithm calculation amount
5 结论
弹载等飞行器的导航系统经常以发射惯性坐标系为基准,且导航系统是典型的非线性系统,其常用的滤波方法为EKF。为了避免EKF滤波算法因线性化展开而引起的导航精度下降问题,本文在设计了发射惯性坐标系下的SINS/CNS/GNSS组合导航系统模型的基础上,采用UKF算法对导航参数进行直接估计,该算法避免对姿态四元数进行直接估计而引起的对姿态四元数控制过于复杂的问题。仿真结果表明,相较于EKF算法,UKF算法能获得更高精度的导航结果,且姿态误差稳定,同时算法能满足系统实时性的需求。
