五棱镜面形误差对中心入射光线的转向角影响
2021-10-27温中凯徐明明张庆君李爽
温中凯,徐明明,张庆君,*,李爽
1. 南京航空航天大学 航天学院,南京 211106 2. 中国空间技术研究院 遥感卫星总体部,北京 100094
1 引言
五棱镜具有使光轴恒转90°且不产生镜像的光学特性,在理论设计和工程应用中的使用十分广泛。国内方面,文献[1-2]利用五棱镜进行多光谱光学系统的光轴平行性标校;文献[3-4]利用五棱镜实现对大口径平面镜的面形检测;文献[5-6]利用五棱镜进行光学系统的波前检测等。国外方面,文献[7]利用五棱镜实现线性光学量子CNOT门的设计;文献[8]利用五棱镜实现对大型光学表面的原位测量;文献[9]利用五棱镜实现快速、高精度的表面坡度测量等。在空间光电跟瞄系统的多光轴平行性标校中,常利用五棱镜将目标靶和CCD分别定位在平行光管的焦面和共轭焦面处,以检测主动式发射系统与被动式接收系统的光轴平行性。而五棱镜制造误差的存在将破坏其垂直折转特性,引起出射光线的转向角偏差,从而影响多光轴平行性的检测精度。因此,有必要对五棱镜进行误差分析以便对结果进行修正。
目前,对五棱镜误差分析的研究多集中在角度制造误差、垂直度误差和姿态误差的影响上,对面形误差影响的研究较少。如文献[10-13]对五棱镜角度制造误差的研究,文献[14-15]对五棱镜垂直度误差的研究,文献[16-20]对五棱镜姿态误差的研究等,均未涉及对五棱镜面形误差影响的研究。此外,面形误差的综合影响十分复杂,需要提出一种降低其研究复杂度的方法。
本文在五棱镜不规则度较小的前提下,利用最佳拟合球面的矢量高度Power适当简化其工作面模型,提出了一种研究五棱镜面形误差对出射光线转向角影响的新方法。在保证计算精度的前提下,降低了出射光线转向角误差数据的维度,推导出了转向角误差的降维计算公式。利用该公式计算主截面方向上转向角误差的最大相对误差为2.14%,最大相对误差低于1.23%的数据占全部计算数据的99%以上,且计算结果与实验测试平均值的偏差在±0.25″以内;计算垂直于主截面方向上转向角误差的最大相对误差仅有0.31%,且计算结果与试验测试平均值的偏差在±0.15″以内。
2 出射光线转向角求解
2.1 建立空间分析坐标系

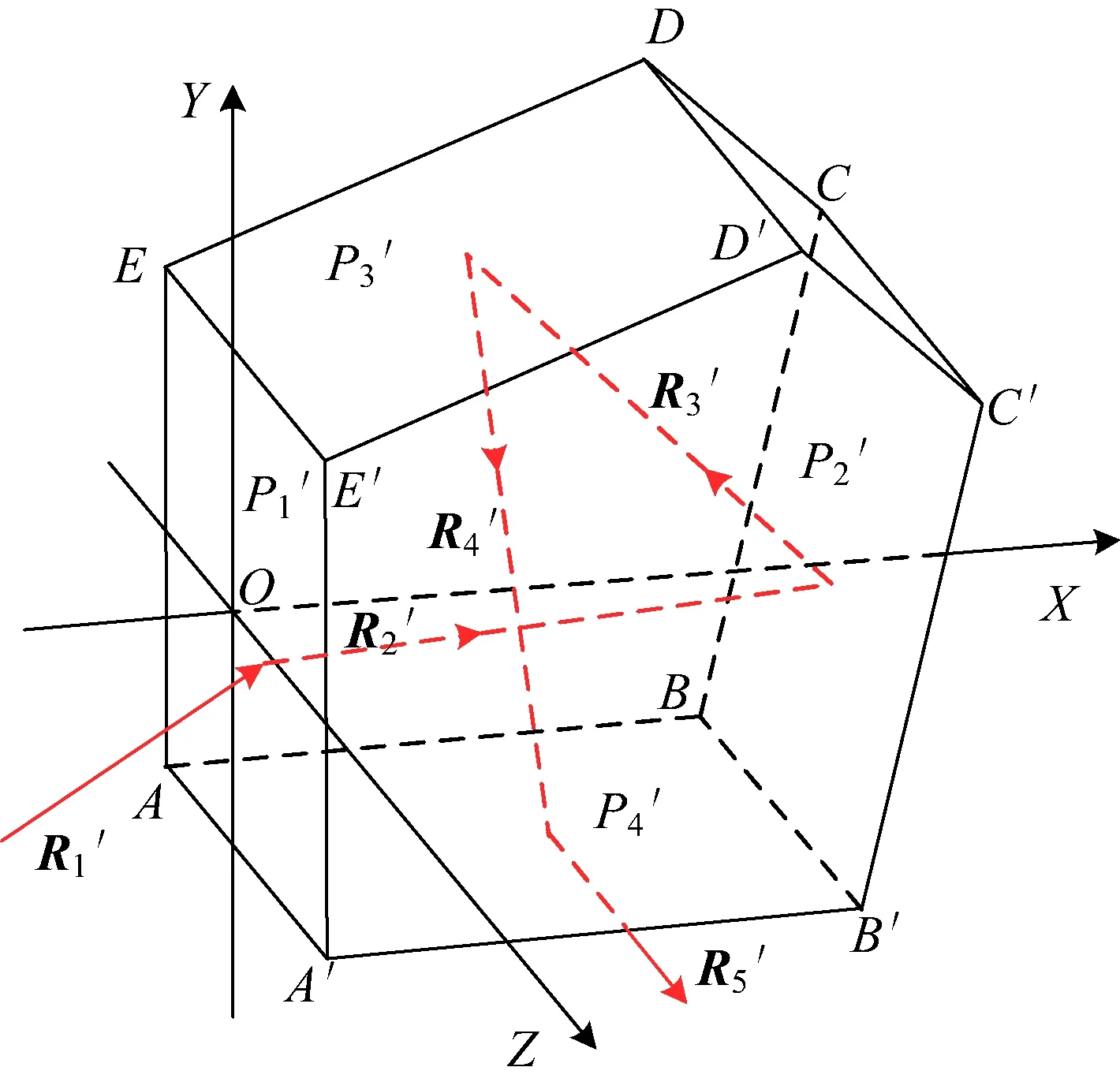
图1 五棱镜光路Fig.1 Light path map of pentaprism
2.2 面形误差的判定方法
传统检测光学平面面形的方法是光学样板法,使用光圈数N与局部光圈数ΔN来衡量面形质量的高低。由于光圈形状的多样性、光圈检查的复杂性,检验员只能凭借经验对干涉图形进行判断。随着光学表面检测技术的发展,特别是数字型激光干涉仪的出现,使得光学零件表面面形误差的精密测量得以实现。利用这种干涉测量设备测出的干涉图形,使用峰谷值PV、均方根值RMS和Power作为衡量面形误差的数字化指标,能精确评估面形误差。
当前航天应用中使用的五棱镜各工作面不规则度很小,即有ΔN≈2|PV-Power|≈0,而Power≠0。根据工程经验,该情况下可用最佳拟合球面的矢高Power表示工作面面形和理想平面波前的光焦度偏差,代替PV与RMS作为衡量面形误差的数字化指标,从而将工作面适当简化成球面以分析其对出射光线转向角的影响。
2.3 求解出射光线转向角
如图2所示,在图1基础上给五棱镜各工作面添加用Power定义的面形误差,设添加面形误差后的五棱镜各工作面为PS(S=1,2,3,4),PS与光线的交点为AS(ASX,ASY,ASZ,),PS在点AS处的单位法向量为NS,此时各光线的单位方向向量分别为R1(x1,y1,z1) ~R5(x5,y5,z5)。
图2中L为干涉仪检测区域口径,|r|为该检测区域曲率半径。Power的符号与干涉仪的检测方式有关,本文设定Power>0时,工作面凹向介质,Power<0时,工作面凸向空气,且令r与Power同号,则由几何关系可得

图2 面形误差分析模型Fig.2 Surface error analysis model

(1)

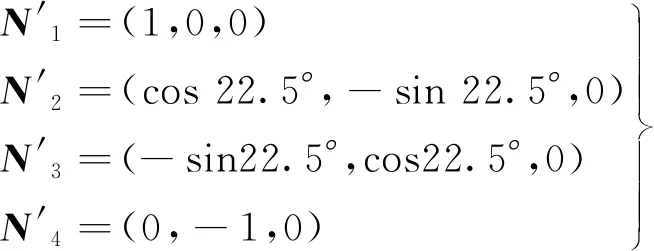
(2)

(3)
式中:φ2=φ3=φ4=-φ1=1。
在实际应用中,入射点A1(A1X,A1Y,A1Z)较易测量的参数是A1Y和A1Z,则A1X的计算公式为:
A1X=O1X+sgn(r1)·

(4)
根据空间解析几何[21]、折射定律与反射定律[22-23]以及式(1)~(4)推导可得出射光线求解公式如下:

(5)

光线在五棱镜主截面即XOY方向的转向角为
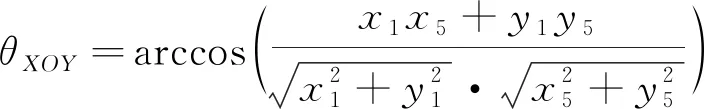
(6)
角度符号定义为:逆着Z轴的方向在五棱镜主截面方向上观察,入射光线在180°以内转向出射光线,顺指针转动为正,逆时针转动为负。
光线在垂直于五棱镜主截面方向上的转向角为
θZ=arcsinz5-arcsinz1
(7)
角度符号定义为:以XOY面为底,并设Z轴正方向为上,在垂直于五棱镜主截面方向上观察,入射光线在180°以内转向出射光线,向上转动为正,向下转动为负。
设五棱镜面形误差所造成出射光线在主截面方向上的转向角误差为ΔθXOY,在垂直于主截面方向上的转向角误差为ΔθZ,则有
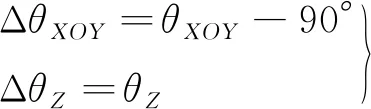
(8)
3 转向角误差的降维分析
3.1 五棱镜初始参数设置

3.2 五棱镜典型应用场景分析
五棱镜常用来对光线进行垂直折转,其典型应用场景之一便是光线以一定入射角从入射面中心区域入射。本文用入射角I和入射方向ω两个变量来定义入射光线的单位方向向量。如图3所示,红色矢量是入射光线的单位方向向量,蓝色矢量是其在YOZ面上的投影,两矢量所构成的平面与XOY面间的二面角便是ω,其符号定义为:右手握住X轴,大拇指指向X轴正向,那么四指的指向就是ω的旋转方向。

图3 入射向量示意Fig.3 Schematic diagram of incident vector
由式(5)~(8)可知,五棱镜出射光线转向角误差受入射角I、入射方向ω和4个工作面Power的共同作用。本文以0.01°为间隔将I从0°取到5°,以1°为间隔将ω从0°取到360°,以0.001λ为间隔分别将Power1~Power4从-0.5λ取到0.5λ,共约1.8×1017个组合,每个组合分别计算ΔθXOY和ΔθZ,共约3.6×1017项7维数据,数据形式如下:
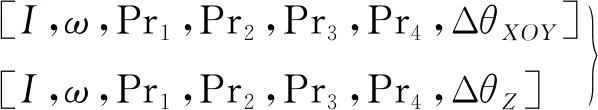
(9)
式中:Power1~Power4分别用Pr1~Pr4表示。显然6个变量对转向角误差的影响不是独立的,而是存在相互影响关系,分析该类7维数据将占用巨大的计算资源。为解决该问题,需要对数据进行降维从而去除各变量间的相互关联。对计算数据分析后发现,若适当舍弃部分计算精度,便可拆解4个面Power的关联性,从而得到以下近似:

(10)
式中:ΔθSXOY和ΔθSZ分别为只有PS存在面形误差而其他面为理想平面时主截面方向和垂直于主截面方向的转向角误差,S=1,2,3,4。式(10)的计算精度如表1所示。
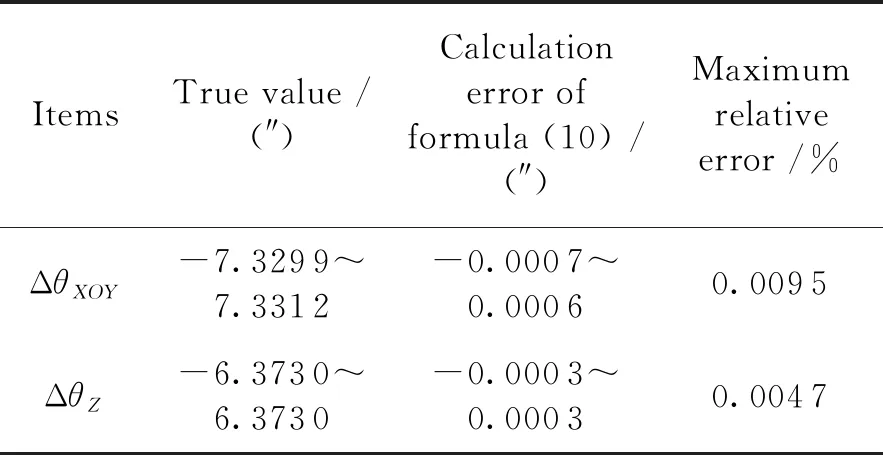
表1 式(10)计算精度统计表
式(10)和表1表明,将五棱镜面形误差对出射光线转向角误差的综合影响转换为各工作面单独对转向角误差的影响是完全可行的,即可将每一个7维数据的计算转换成4个4维数据的计算。
通过对不同入射角I下ΔθSXOY和ΔθSZ的图像进行对比后发现,无论入射角I为何值,对应的ΔθSXOY和ΔθSZ均拥有相同的形状和相同的变化趋势,且不同入射角I对应的ΔθSXOY和ΔθSZ存在明显的倍数关系,故本文合理假设:当入射角I变为KI,而其他参数保持不变时,ΔθSXOY和ΔθSZ近似变为KΔθSXOY和KΔθSZ。如I=1°和I=3°时,各工作面Power和光线入射方向ω影响下的转向角误差的数值变化分别如图4和图5所示。根据计算,当光线从入射面中心入射时,P1的面形误差几乎不产生任何转向角误差,故图4和图5中省略了有关P1的数据。

图4 I = 1°时转向角误差数值变化趋势Fig.4 Numerical variation trend of steering angle error when I=1°

图5 I = 3°时转向角误差数值变化趋势Fig.5 Numerical variation trend of steering angle error when I=3°
通过计算可得该假设方法在I= 3°作为对比基准时的计算精度如表2所示。

表2 近似方法计算精度统计
由表2可知该方法完全可行,即可通过舍弃部分计算精度将7维数据中入射角I的影响除去,结合式(10)便可将6个非独立随机变量影响下的7维数据的计算分析问题转换为各工作面Power和光线入射方向ω影响下的3维数据的计算分析问题。
由图4和图5知,当PowerS(S=1,2,3,4)分别为定值时,转向角误差与ω近似成正弦或余弦关系,近似计算如下:
(11)
式中:幅值ASXOY和ASZ分别由该PowerS下ΔθSXOY和ΔθSZ波峰或波谷处的取值确定,且式(11)的计算精度如表3所示。

表3 式(11)计算精度统计
当ω为定值时,转向角误差与PowerS(S=1,2,3,4)近似成线性关系,且近似计算如下:

(12)
式中:斜率KSXOY和KSZ分别由该ω下ΔθSXOY和ΔθSZ在PowerS= ±0.5λ处的取值确定,式(12)的计算精度如表4所示。
由表3和表4可知,3维数据可进一步去除Power和ω的相互影响,从而完全去除影响出射光线转向角误差的6个非独立随机变量间的相互关联。由式(10)~(12)以及表2中的近似方法可得ΔθXOY和ΔθZ的降维计算公式为:

表4 式(12)计算精度统计
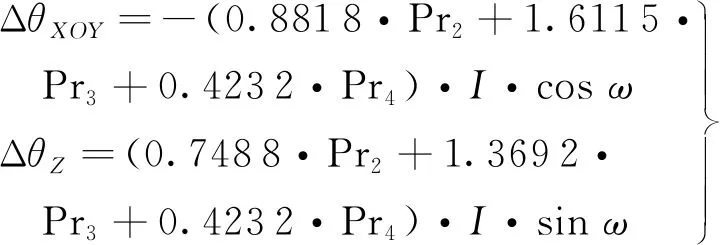
(13)
式中:Power以λ为单位,I和ω均以度为单位,且降维公式的计算精度如表5所示。

表5 降维公式计算精度统计表
由表5可知,降维公式的计算误差和最大相对误差均较小,且进一步分析可知,应用降维公式计算ΔθXOY的最大相对误差低于1.23%的数据占全部计算数据的99%以上。此外,由式(13)可知,只需五棱镜各工作面的Power值配置合理,便可减小甚至消除五棱镜面形误差对出射光线转向角的影响。
4 试验测试与结果
如图6所示,将五棱镜固定在高精度调整平台上并放置在干涉仪前,干涉仪发出的632.8 nm波段的平行光束一部分经五棱镜入射面反射,另一部分经五棱镜到达经纬仪。保持五棱镜固定,将入射面反射像的干涉条纹调整至一个条纹以内,用经纬仪瞄准干涉仪光轴,将此时经纬仪的读数清零,保持经纬仪不动,用其瞄准经五棱镜折转后的光束光轴,并记录读数,该读数为干涉仪正入射时的转角,可通过该值计算五棱镜角度制造误差的影响。转动高精度调整平台,即可测试平行光束的光轴变化。此外,在五棱镜入射面前放置一个可移动并且可以调节口径大小的小孔光阑,从而确保平行光束从入射面中心入射。对入射光线的每一种入射角I和光线入射方向ω下的五棱镜均重复进行100次测试,对测试数据进行数据修正以去除五棱镜角度制造误差的影响,并取平均值作为最终测试结果。

图6 试验装置Fig.6 Experimental devices
将降维公式的计算结果与最终测试结果的偏差绝对值整理成表6和表7,由于0~180°与180°~360°之间的数据存在对称相似现象,故表中省略了180°~360°的数据,且表中第一列为入射方向ω的数据,表中第一行为入射角I的数据,表中其余部分为相应转向角误差ΔθXOY和ΔθZ的偏差绝对值数据。
将表6和表7的试验结果与降维计算公式的计算结果对比后发现:主截面方向和垂直于主截面方向上转向角误差的试验测试平均值与降维公式计算值的偏差分别在±0.25″和±0.15″以内,这是完全可以接受的。

表6 降维公式计算结果与主截面方向测试结果偏差

表7 降维公式计算结果与垂直于主截面方向测试结果偏差
5 结论
针对五棱镜面形误差造成出射光线转向角误差的问题,本文通过适当简化模型,将影响出射光线转向角误差的因素限定在了6个非独立随机变量的共同作用上,并通过降维分析去除了6个变量间的相互关联,推导出了降维后的出射光线转向角误差计算公式,并得出以下结论:
1)保证光线从入射面中心区域入射可消除五棱镜入射面面形误差对出射光线转向角的影响。
2)光线入射角越大,面形误差造成的出射光线转向角误差越大,故光线垂直于入射面入射可降低五棱镜面形误差对出射光线转向角的影响。
3)五棱镜精度越高,面形误差造成的转向角误差越小,但成本也越高。由降维公式分析可知,对主截面方向转向角精度要求较高的情况,只需选用0.881 8·Pr2+1.611 5·Pr3+0.423 2·Pr4最小的五棱镜便可减小面形误差的影响,从而用低精度五棱镜实现高精度五棱镜的效果;对垂直于主截面方向转向角精度要求较高的情况,只需选用0.748 8·Pr2+1.369 2·Pr3+0.423 2·Pr4最小的五棱镜便可减小面形误差的影响,从而用低精度五棱镜实现高精度五棱镜的效果。
