路基智能压实关键控制参数动态仿真及演变规律

马源，方周，韩涛，汪双杰，张伟光，陈建兵，李金平，李贝基

(1.东南大学交通学院，江苏南京，210096；2.中交第一公路勘察设计研究院有限公司陕西西安，710075)

压实是道路施工的重要过程[1-3]。良好的道路压实效果可以显著提高道路结构的强度、刚度和稳定性，从而保证道路的使用寿命[4-6]。传统压实工艺和质量检测方法在一定时期内有力保障了道路的建设质量。然而，随着变革性技术的快速发展其不足日益凸显[7-8]，例如：1)压实施工时，振动压路机参数的选取多依赖于施工人员的经验，如碾压速度、压实遍数、激振频率和激振幅值。压实过程中的压实状态不可知，压实的结束时间严重依赖于操作人员的经验，过压、欠压的情况普遍存在。2)压实质量的检测只是实现了“点”的检测，无法实现全面性检测。压实质量检测为“事后”检测方法，无法体现过程控制。与此同时，常规的传统压实质量检测方法如环刀法、灌砂法[9]等具有一定的破坏性。3)在压实过程中忽略了压实质量均匀性的检测。上述传统压实技术和质量检测方法存在的不足往往成为道路使用寿命降低、养护成本增加的重要诱因。

由于传统压实及压实质量检测方法存在上述不足，智能压实技术应运而生。智能压实技术对于解决上述压实质量控制的不足具有非常显著的优势。智能压实技术是采用计算机技术、高精密传感技术以及定位技术等高新技术集成的一套新型压实技术。它可以实现对智能压路机的综合控制，并将当前压实状态以及反馈调节等信息传输给用户。

目前，智能压实质量的评价指标种类有以下3类：1)基于加速度信号的指标，这类指标主要包括加速度幅值指标[10]和谐波比指标[11-12]，如压实质量测量值(compaction measurement value，CMV)和压实质量控制值(compaction control value，CCV)；2)基于刚度或力学参数类的压实质量评价指标[13-15]，如土体抗力、振动模量；3)基于能量法的指标，如Omega 值和前进压实效率值(machine drive power,MDP)。其中，由于加速度信号类指标计算简便，且能较精确地反映压实质量，因此，目前应用最广泛的指标是CMV。虽然智能压实技术在近年来得到迅速发展，但仍存在以下问题[12,15-17]：1)在目前智能压实技术数值仿真方面的研究中没有考虑到被压实结构层力学参数的动态变化[18-19]。例如，在路基土智能压实过程中，随着压实的进行，路基土的各项力学指标是在发生变化的，其黏聚力c、内摩擦角φ都会随着压实质量的提升而增大。若不将其考虑到数值仿真的过程中，则会使得数值仿真结果与实际情况存在差异，从而导致数值仿真的结果出现误差。2)目前在智能压实过程中，针对因素对最终压实质量影响的研究较少，这样就会导致智能压实技术的机理模糊，更多地依赖现场试验结果来发展智能压实技术，从而导致智能压实的理论研究薄弱。3)智能压实技术能够实现全面的压实质量检测，但针对智能压实质量均匀性评价研究较少。压实质量是否达到标准要求是检验道路压实施工质量的一个标准，而另一个重要的标准则是压实质量的均匀性是否满足要求。若压实质量均匀性分布存在问题，则可能导致不均匀沉降等问题出现。

为了提高智能压实数值仿真的准确性，研究不同影响因素对压实质量的影响程度，进一步对智能压实质量均匀性展开分析。本文作者在分析CMV 作为智能压实质量评价指标的基础上，建立压实过程参数动态变化的仿真模型，研究不同压实参数变化对CMV的影响趋势及程度。在此基础上，通过单变量统计学正态分布3σ准则的方法，研究其压实质量均匀性，同时通过空间统计学半变异函数的方法，研究智能压实影响范围。

1 研究方法

构建压实过程参数动态变化仿真模型，分析不同压实参数(碾压速度、激振力、自重、激振频率以及碾压遍数)对智能压实控制参数CMV的影响趋势及程度，明确影响CMV的关键因素。在此基础上，通过单变量统计学正态分布3σ准则的方法，对智能压实质量的奇异点进行了检测，分析智能压实控制条件下的压实均匀性。进而通过空间统计学半变异函数的方法，分析不同空间距离状态下各个点位的智能压实质量的相关程度，得到智能压实施工时的影响范围。

1.1 CMV计算原理及变化规律

当智能压路机以一定的碾压速度对路基进行压实施工时，其振动轮在偏心块不断旋转的作用下产生激振力。激振力与智能压路机的自重共同作用在路基土上，使得被压实的土体由静止状态变为振动状态。土体也逐渐由松散变得密实。在这个过程中，土体的压实质量与刚度都会随着压实的进行而提高。

研究表明，路基土的刚度与振动轮的竖向加速度信号密切相关[20]。在压实施工的初始阶段，土体处于相对松散的状态，压实质量与刚度较小，因此，土体对振动轮的抵抗力(Fs)也相对较小，如图1(a)所示。随着压实的进行，土体的压实质量和刚度增大，伴随而来的路基土对振动轮的反作用力也逐渐增大，如图1(b)所示。

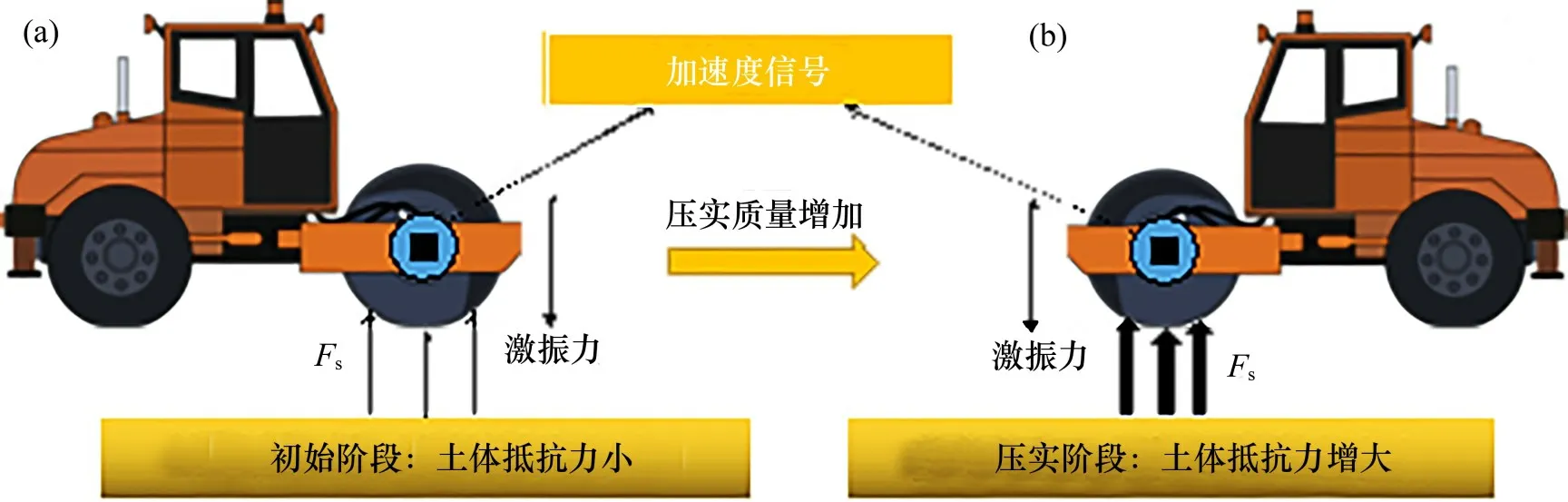
图1 初始阶段中振动轮与土体相互作用关系和压实过程中振动轮与土体相互作用关系Fig.1 Interaction between vibration wheel and soil in the initial stage and interaction between vibration wheel and soil during compaction

在压实的初始阶段，由于土体对振动轮的抵抗力较小，振动轮的偏心块也处于初始位置(相位角为0°)，振动轮产生的激振力是一个标准的正弦函数，由此采集的振动轮加速度信号(a)也是一个正弦函数，如图2(a)所示。当路基处于压实过程时，随着路基土体抵抗力的增大，振动轮加速度信号不再是单一的正弦函数，而是一个由多个弦函数组成的复杂信号，由于多个弦函数的叠加，幅值也相应地增大，如图2(b)所示。

图2 初始阶段振动轮加速度时域信号和压实过程中振动轮加速度时域信号Fig.2 Initial vibration wheel acceleration time domain signal and time domain signal of acceleration of vibrating wheel during compaction

在压实的初始阶段，振动轮的加速度时域信号是单一的正弦函数，经离散傅里叶变换之后得到加速度频域信号，只有一次谐波(基波)的幅值，如图3(a)所示(其中，f0为基波频率，A为加速度幅值)。而随着压实的进行，振动轮加速度的频域信号出现二次谐波，如图3(b)所示。此时，通过二次谐波与一次谐波幅值的比值关系，来判断当前压实状态。

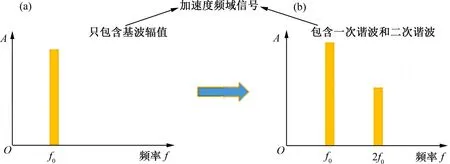
图3 初始阶段振动轮加速度频域信号和压实过程中振动轮加速度频域信号Fig.3 Frequency domain signal of acceleration of vibration wheel in initial stage and frequency domain signal of acceleration of vibration wheel during compaction

1.2 数值仿真模型构建

建立二维数值仿真模型，对智能压实过程中的施工工艺参数进行分析。为了实现压实参数的动态调整，利用ABAQUS 商用软件进行有限元数值仿真模型的构建和二次开发[21-22]，通过编写UMAT 子程序，实现智能压实过程中土体参数的动态变化[23-24]。

1)路基结构和网格划分。目前研究表明，压实过程中振动轮在水平方向的影响范围为3～5 m。因此，在建立数值仿真模型时，将水平方向的尺寸定义为10 m，以消除尺寸效应带来的影响。在实际施工时，路基每层松铺厚度为20～30 cm。因此，本文将上层松铺厚度定义为30 cm，下部基础定义为3.7 m。表1所示为路基土初始压实状态下的参数。

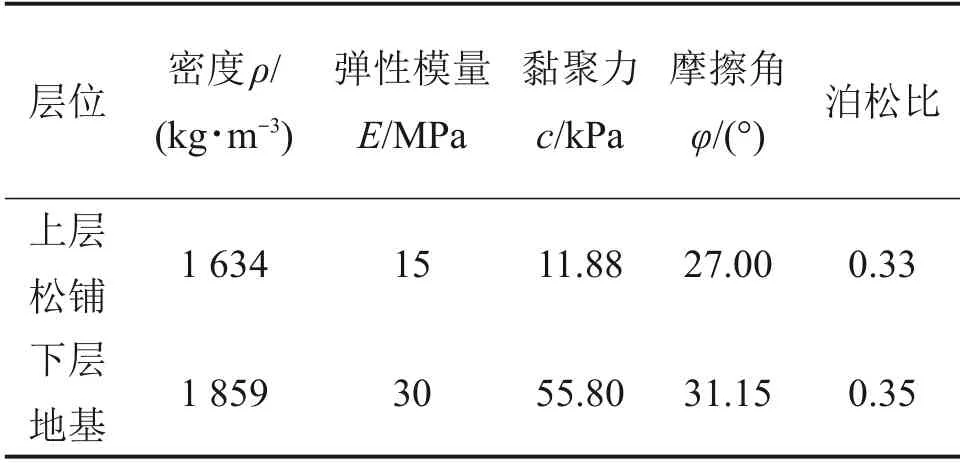
表1 路基土初始压实状态参数Table 1 Parameters of initial compaction state of subgrade soil

网格密度的选取也是数值仿真中的关键环节。网格密度的选择既要保证数值模拟的精度，又要保证足够的计算效率。在本研究中，为了同时平衡计算效率与精度，在保证计算精度为第一原则的基础上，尽可能提高计算效率。因此。在加载区域附近使用细网格，而在远离加载区域使用粗网格。精细网格与粗网格采用梯度网格连接。所选网格尺寸为加载区域0.05 m，边缘区域0.2 m，如图4所示。

图4 路基结构示意图和有限元数值仿真网格划分图Fig.4 Roadbed structure and finite element numerical simulation grid division diagram

2)荷载及边界条件。在边界条件方面，由于模型尺寸足够大，边界条件不会对仿真结果产生明显影响，因此，将水平两侧及地面设置为固定约束。荷载施加情况，将在后面正交试验中压路机参数中给出。仿真过程中，分别进行1～4次压实作业并提取数据。

3)压实参数动态变化的仿真实现。在压实过程中，土体的抗剪强度指标(黏聚力c、内摩擦角φ)随压实不断变化，所建立的模型需能够反映上述强度指标的变化特征，具体实现步骤如下：首先，选择压实度K作为数值仿真中的场变量，建立压实度K与土基应变的关系；其次，建立抗剪强度指标与场变量压实度K的关系；最后，通过编写UMAT子程序，建立应变与抗剪强度之间的关系，实现抗剪强度在压实过程中的实时调整。

1.2.1 场变量压实度与土体应变之间的关系

在压实过程中，路基土的应变可与压实度建立关联[16-18]，因此，可以通过应变进行压实度的计算。在仿真模型建立过程中进行以下假设：1)路基压实过程中在水平和竖直方向的应变相较于模型尺寸可忽略不计，压实过程中模型形状被认为是矩形；2)路基土在初始状态和压实过程中连续、均匀、各向同性。

模型中设定z方向宽度为1，且不发生变形，即应变ε3=0。初始压实度设定为0.8。路基土模型在压实过程中的体积为

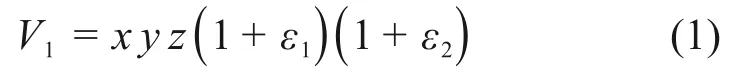
式中：x为模型长度；y为模型高度。

压实度K为

密度ρ为

式中：K为压实度；ρ为当前压实度K对应下的密度，kg/m3；ρmax为压实材料的最大干密度，kg/m3；m为密度ρ对应的质量，kg；V为密度ρ对应的体积，m3。

在压实过程中，土体质量m为定值，土体最大干密度ρmax不变，只有体积V和密度ρ发生实时变化。联立方程(1)～(3)，可得

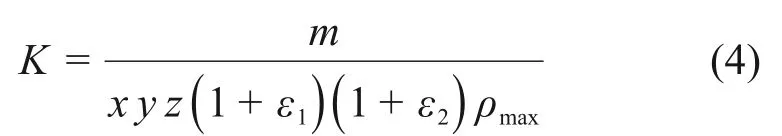
且有

式中：K0为初始压实度。

将式(4)和(5)联立，可得：

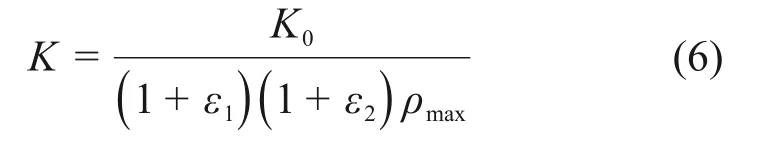
将由初始设定压实度为0.8代入式(6)可得

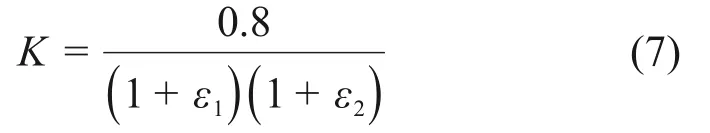
至此，便通过数学建模的方法，确定压实度K与应变ε之间的关系。

1.2.2 抗剪强度指标与场变量压实度K

MA 等[25]在之前的研究中，通过对压实度为0.80，0.85，0.90，0.93，0.94，0.96 和1.00 的试件进行直剪试验，试验结果如表2所示。

表2 压实度与黏聚力、内摩擦角试验结果Table 2 Test results of compaction degree,cohesion and internal friction angle

通过拟合，得到压实度K与黏聚力c以及压实度K与内摩擦角φ的关系式分别为

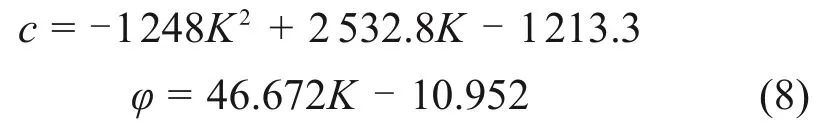
由此便得到了应变与压实度、抗剪强度指标与压实度的关系，进而可在有限元模型中建立应变与抗剪强度指标的关系。

1.3 有限元数值仿真正交试验设计

由于在研究不同施工参数对压实质量的影响时，本文主要研究的施工参数有5个因素，而每个参数的水平项有4 项，全部的试验工况将会有54=625组。因此，本文为了提高计算效率，设计5因素4水平正交试验表，如表3所示。正交试验只需要进行16 组试验，便可以对不用施工参数压实质量的影响进行分析，如表4所示。本文研究的5个因素分别为碾压速度、激振力，自重，激振频率和碾压遍数。每个研究因素对应4 个水平变量。水平变量1和水平变量4分别对应目前大多智能压实施工参数的最大值与最小值，水平变量2和水平变量3分别采用内插法确定。

表3 5因素4水平正交试验表Table 3 Five factors and four levels of orthogonal test table

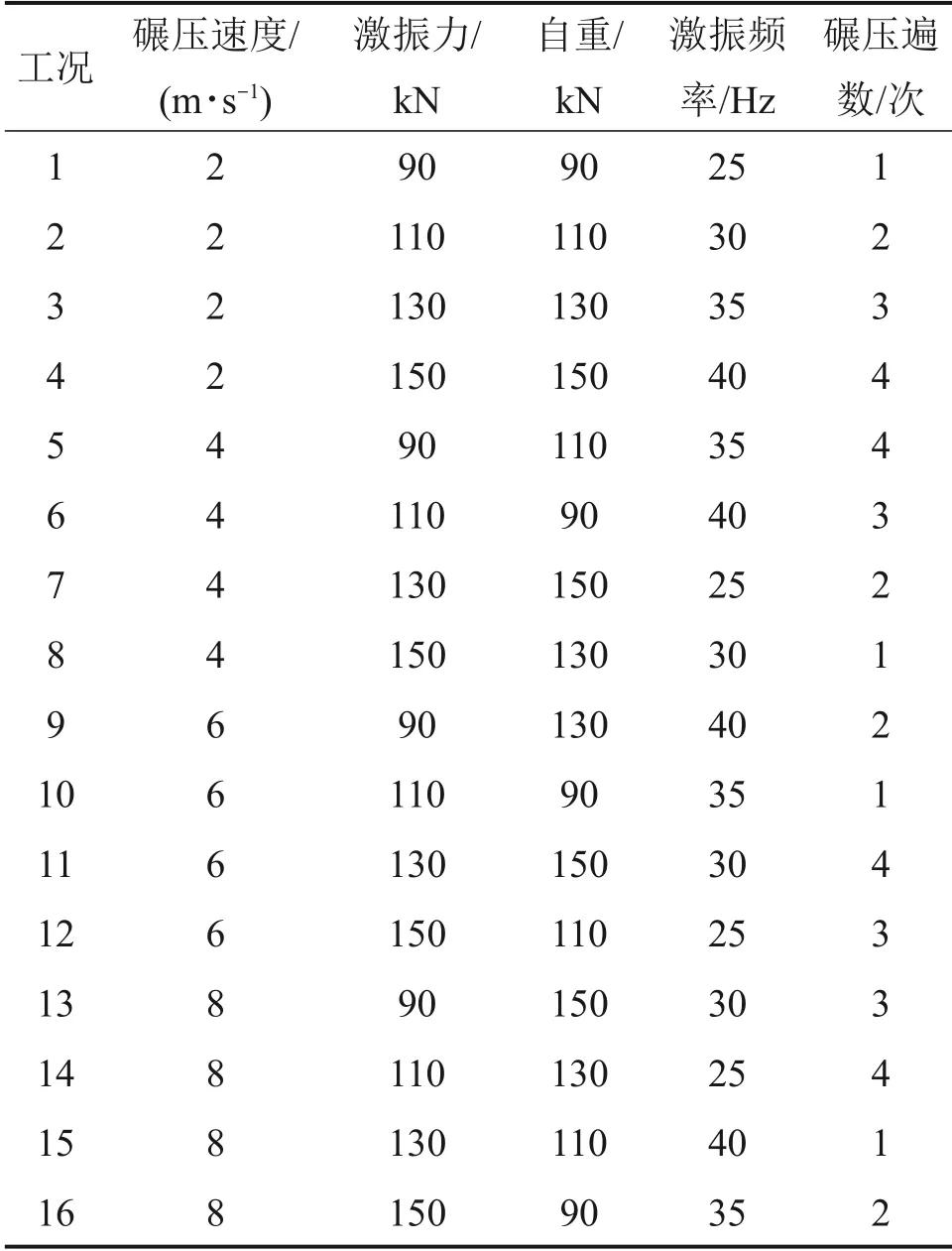
表4 正交试验工况Table 4 Orthogonal test condition

1.4 基于统计学方法的压实质量均匀性与影响范围计算

正态分布是数学、物理和工程中重要的概率分布，在统计学的许多方面都有很大的影响以及较广的应用[26]。

图5所示为正态分布示意图，其中，σ为样本的标准差，μ为样本的平均值。3σ准则是指一个数值位于(σ-3μ，σ+3μ)区间的概率为0.997，而没有位于这个区间的数值，则可以认为是异常点，即压实量不均匀的位置。

图5 正态分布示意图Fig.5 Diagram of normal distribution

与单变量统计学的没有考虑空间距离不同，空间统计学不仅考虑样本值的大小，同样重视样本之间的空间位置与关系，半变异函数是空间统计学中用来描述样本空间关系的常用工具。半变异函数的定义如下：

式中：h为空间距离；Z(xi)为xi点的样本值；n(h)为空间距离为h点的组数。

半变异函数中有3 个重要参数，分别是变程、基台及块金值，如图6所示。当样本之间存在空间相关关系时，半变异函数变化曲线会随着空间距离的增加而逐渐增加并趋于稳定。曲线第一次出现水平时对应的横坐标(空间距离)即为变程，在变程范围之内，样本点具有空间相关性，在变程范围之外，样本点不具备空间相关性。半变异函数趋于稳定时对应的纵坐标成为基台，基台表示样本点的离散程度。此外，原则上来讲，在h=0 时，半变异函数为0，但由于测量误差的影响，半变异函数有时不为0，此时，对应的纵坐标称为块金值。

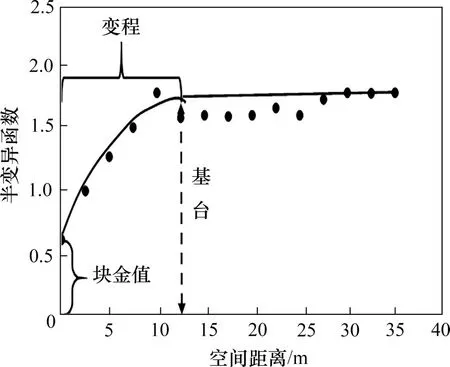
图6 经典的样本半变异函数图Fig.6 Classic sample semivariogram

为了得到一定距离下半变异函数并建立其代数公式，通常需要对理论模型进行拟合。由于压实质量的变化是随施工进行呈正相关发展，也不存在“指数爆炸”情况，不要通过特殊的模型例如随机模型、指数模型进行拟合。与此同时，通过球形模型对智能压实质量进行拟合，能够保证其拟合精度。因此，对于智能压实的数值仿真，本文选择球形模型来拟合半变异函数图。其数学表达式如下：

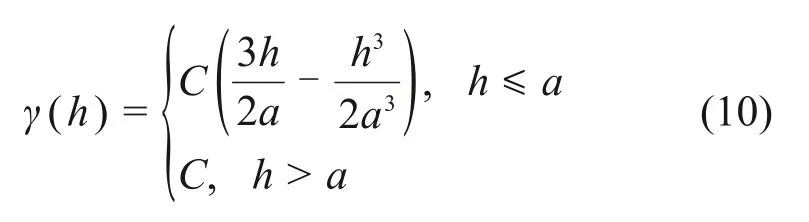
式中：C为基台，C=σ2(σ2是样本的方差)；a为变程。

2 结果和分析

通过对ABAQUS 有限元数值仿真软件的二次开发，设计影响压实质量因素的正交试验，并进行单因素分析，得到影响压实质量最为关键的因素。选择正交试验第4组试验工况，通过单变量统计学的方法和空间统计学的方法分别分析压实质量均匀性以及智能压实技术的影响范围。

2.1 压实遍数与竖向位移（压实度）相关性分析

图7所示为路基土竖向位移随压实过程的变化趋势。由图7可以看出：

图7 竖向位移随时间变化曲线和压实度变化趋势Fig.7 Vertical displacement and time change curve and compaction degree and rolling times change curve

1)在同一次压实过程中，被压区域竖向位移在同一次压实过程中的变化幅度较小。这是由于在每一条带中，路基土参数是相同的，荷载施加条件也是相同的，因此，在同一次压实过程中，竖向位移的变化总是稳定在同一个值附近。

2)随着碾压遍数增加，竖向位移逐渐增大。随着压实的进行，路基土的压实度稳步增大，因此，竖向位移也增大。但不难发现，随着压实的进行，竖向位移的增大幅度逐渐减小。这是由于当路基土达到一定压实质量时，用同样的压实工艺对其进行压实，更难被压实。在压实质量上表现出来的就是，压实质量增长速度变慢。因此，随着碾压遍数的增加，竖向位移的增长速度减缓。

同样对数值仿真振动轮加速度信号的结果进行采集分析。整体上，第n次(n∈[1，2，3，4])压实长度为4 m，每一次压实分为前进方向和后退方向，共计8 m，振动压实每2 m计算1次CMV，共计算5次，最后求取其平均值，作为本次智能压实质量指标值。

2.2 压实遍数与CMV的相关性分析

数值仿真加速度时域信号如图8所示。

CMV由下式计算得到：

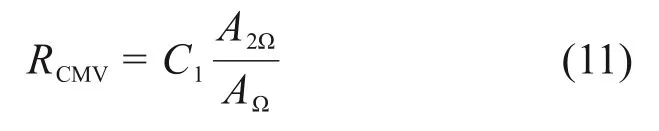
式中：RCMV为压实质量测量值；AΩ为基波幅值；A2Ω为二次谐波幅值；C1为常数项，本文取100。

计算得到4 次压实的CMV 平均值及误差图，如图9所示。从图8和图9可以看出：

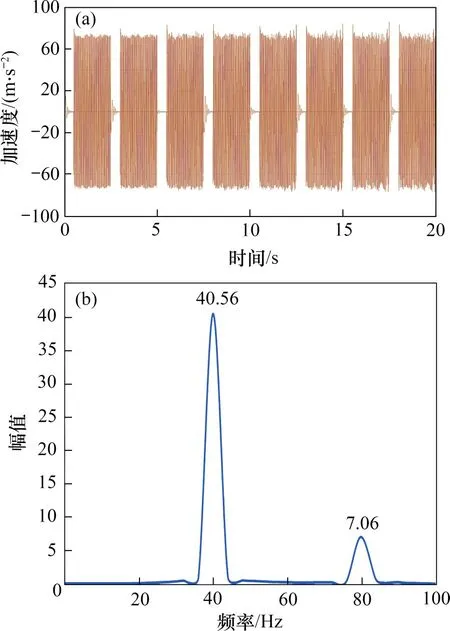
图8 加速度时域信号图和加速度频域信号Fig.8 Acceleration time domain signal diagram and schematic diagram of acceleration frequency domain signal

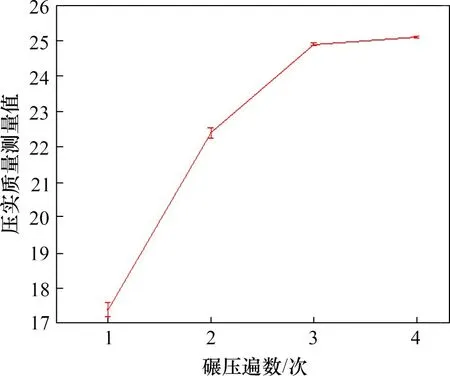
图9 第4组工况CMV误差图Fig.9 CMV error bar of the fourth group condition

1)智能压路机在振动压实过程中，加速度信号相对均匀，且幅值相近。通过对振动轮加速度信号进行离散傅里叶变换，可以振动加速度频谱图。频谱图中较清晰地显示基波幅值以及二次谐波幅值，且基波对应的频率为40 Hz，这与第4 组工况激振频率40 Hz也是相符的。

2)从第1遍至第4遍压实过程中，同一次碾压过程中CMV 的变异系数分别为0.019，0.016，0.005 和0.004，这表明在同一压实过程中，CMV相对稳定，离散性小，因此，将CMV作为压实质量评价指标是合理的。与此同时，CMV 的离散程度随着碾压遍数增加呈逐渐减小的趋势，这表明CMV在随着压实的进行也逐渐趋于稳定。

3)随着压实的进行，CMV 是逐渐呈上升趋势。从图9可以看出：CMV 平均值随着碾压遍数增大，但增大的幅度逐渐减小。CMV 可以反映路基土的刚度，在压实初期，刚度随压实的进行，增大的幅度较大，CMV 也有较大增长。当路基达到一定压实质量之后，就难以被压实，此时对路基继续进行压实，刚度增大幅度减缓，CMV 的增长速率液同时减小。

2.3 正交试验结果分析

本文采用数值模拟设计正交试验的方法，得到表5所示的16 组正交试验对应的智能压实质量评价指标CMV。

表5 各工况下智能压实质量评价指标CMV平均值Table 5 Average of intelligent compaction quality evaluation index CMV under different working conditions

根据表5的计算结果，采用极差分析法进行智能压实质量主控因素分析。分析过程如下：可假设mij为第i因素j水平所对应的计算指标总和，为mij的平均值。反映第i因素对智能压实质量评价指标CMV的影响，极差Ri=max()-min()。Ri越大，说明该因素对智能压实质量评价指标CMV 的影响也越大，对应的因素是最主要的因素，min(Ri)对应的因素为所有因素中影响最小的因素。正交试验极差分析结果如表6所示。从表6可以看出：

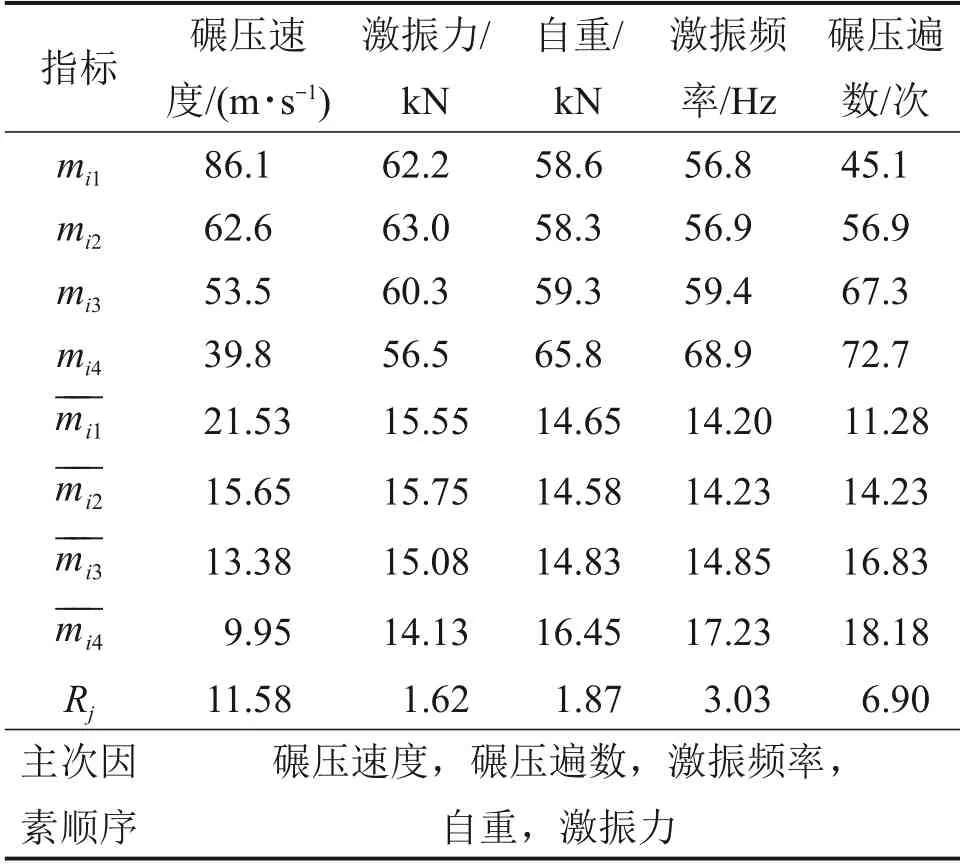
表6 正交试验极差分析表Table 6 Range analysis table of orthogonal test

1)碾压速度、碾压遍数、激振频率、自重、激振力的极差逐渐减小。这说明其对智能压实质量的影响依次减小，影响最大的2个因素为碾压速度和碾压遍数。

2)碾压速度与碾压遍数对智能压实质量的影响远比其他3 个影响因素的大。随着碾压速度增大，mij逐渐减小，而碾压遍数呈相反关系。这表明当碾压速度降低时，压实质量会增大，当碾压遍数增大时，也会达到同样的效果。

2.4 压实质量均匀性及智能压实影响范围分析

从表4可以看出：在第4组工况时，第一次出现碾压遍数为4 次的工况，4 次碾压遍数是碾压遍数这一因素的上限取值，能够更全面地反映试验结果，且各工况表现出的变化规律相对一致。因此，为了能够获取更多的样本，更为全面地展示压实质量均匀性分析以及影响范围分析，本文以第4组正交试验工况为例，通过单变量统计学的方法，计算智能压实质量均匀性。通过空间统计学的方法，计算其压实影响范围。

通过计算得到的第4 组正交试验的5 个CMV分别为25.0，25.0，25.2，25.2 和25.1，由此可计算得到其平均值μ=25.1，样本标准差σ=0.1，如表7所示。

表7 CMV单变量统计学分析表Table 7 Univariate statistics of CMV

由此确定的[μ-3σ，μ+3σ]为[24.8，25.4]，即若有CMV没有处于这个区间，则可认为该处的CMV是奇异点，需要进行重新检测。由表7可以看出：第4 组正交试验计算得到的CMV 皆位于区间内。因此，第4组工况下得到的智能压实质量均匀性满足要求。

通过空间统计学的方法，计算智能压实的影响范围。各点CMV的分布情况如图10所示。

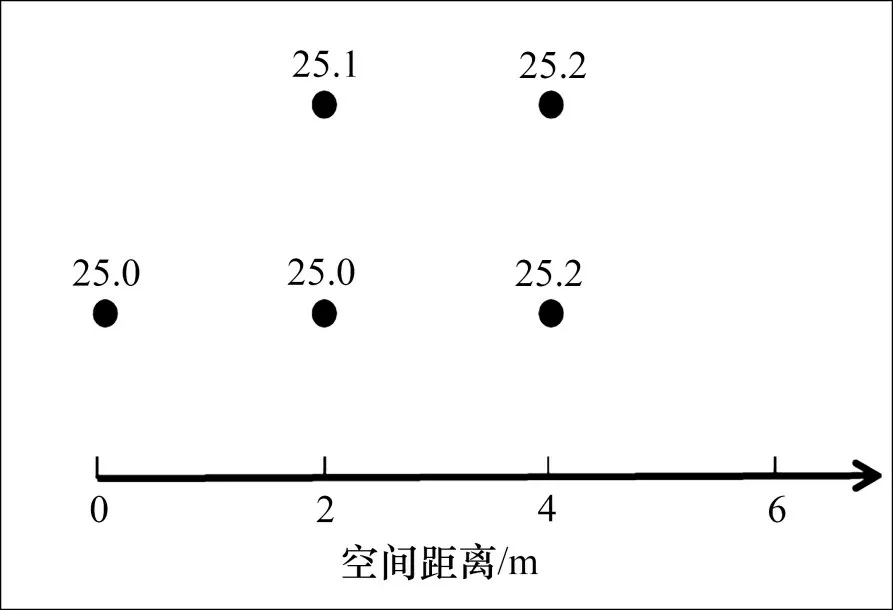
图10 CMV一维取样分布图Fig.10 One-dimensional sampling distribution of CMV

以空间距离h=2 为例，计算CMV 的半变异函数值，如表8所示。

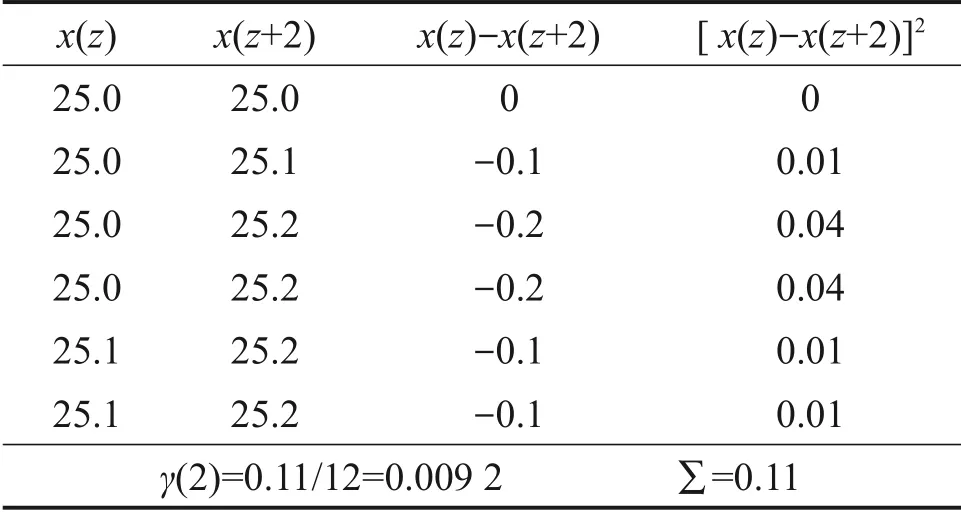
表8 h=2时γ(h)的计算过程Table 8 Calculation process of γ(h)when h=2

基于图10中CMV的半变异函数计算结果如表9所示。

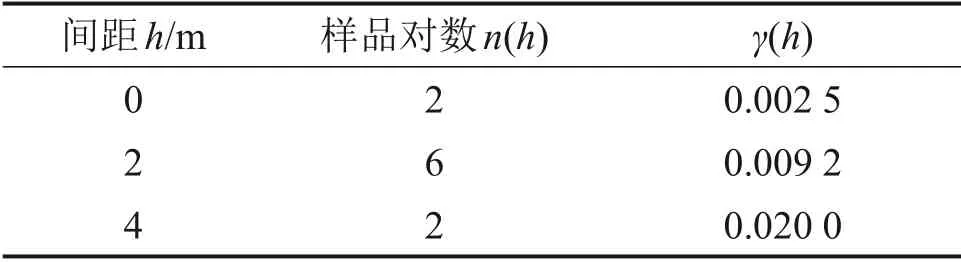
表9 基于图10计算CMV半变异函数计算结果Table 9 Calculation of CMV semivariogram function based on Fig.10

将表9的计算结果绘于图11中，可得到实验半变异函数曲线。从图11可以看出：

1)随着空间距离的增大，半变异函数也逐渐增大。这表明随着空间距离的增大，各个点位之间的空间关联程度降低。

2)通过球形模型对实验半变异函数进行拟合，通常认为半变异函数γ(h)第一次达到σ2=0.01 时对应的横坐标是变程a的2/3。从图11可以看出：空间距离大致在2.1 m时出现第一次γ(h)=0.01，这表明变程a约为3.15 m，这与前面提到的智能压实影响范围为3～5 m是相符的。

此外，值得注意的是，空间距离较小，试验半变异函数的曲线规律性不是很明显。由于受数值仿真效率的限制，若建立大尺寸数值仿真模型，会使得计算效率降低。因此，本文建立的数值仿真模型在长度方向只有4 m，这可能导致由于空间限制使得计算结果不精确。

3 结论

1)通过UMAT 子程序，对有限元数值仿真软件进行二次开发并建模对智能压实进行数值仿真模拟，实现了参数的动态变化。从数值仿真结果来看，最大竖向位移是与理论计算结果相符的。这也验证了有限元数值仿真软件二次开发的准确性。

2)正交试验结果表明对压实质量影响最大的因素是碾压速度，其次是碾压遍数，而激振力、自重、激振频率对压实质量的影响较小。

3)本文提出了正态分布3σ原则用于分析智能压实质量的均匀程度，并验证了其合理性。同时，本文提出用空间统计学分析统计学半变异函数的方法对智能压实影响范围进行分析。最终计算得出在智能压实过程中，会对周围半径为3.15 m 的区域产生影响。

4)由于本文建立的数值仿真模型考虑到边界条件及计算效率。虽然构建的有限元尺寸模型的长度为10 m，但真正用于智能压实作业区域的长度仅为4 m。仅通过4 m 的压实条带长度对压实质量的均匀性以及影响范围进行分析，这样可能因采样数据较少，增大计算结果的偶然性，致使计算结果出现偏差的概率增大。后续工作可在时间充足的情况下，通过建立更大尺寸的模型，获取更多试验数据，从而使计算精度得到保证。