纤维水泥土中GFRP筋黏结性能及考虑肋效应的黏结滑移模型试验研究

2021-10-25黄晓实陈昌富毛凤山朱世民蔡焕

中南大学学报（自然科学版） 2021年7期

黄晓实，陈昌富，毛凤山，朱世民，蔡焕

(1.湖南大学建筑安全与节能教育部重点实验室，湖南长沙，410082；2.湖南大学土木工程学院，湖南长沙，410082)

劲芯水泥土复合桩[1]、加筋水泥土锚[2]常用于软土地区的路基加固和基坑支护，其中，劲芯-水泥土界面的黏结性能对劲芯水泥土桩(锚)的承载性能有重要影响。然而，在含盐量较高的海边软土地区采用钢筋作为劲芯时，筋体存在锈蚀破坏的风险，因而，工程中常采用具有良好抗腐蚀性能的GFRP筋(玻璃纤维增强塑料筋)作为加筋的劲芯。大量研究结果表明[3-7]，在水泥土中掺纤维可有效提高其抗拉强度和抗弯强度。此外，在水泥土中加入适量的建筑垃圾不仅可改善水泥土的性能，而且可实现废物利用，因此，研究高含盐量海水环境下纤维水泥土中GFRP筋的黏结性能和黏结滑移模型，对深入了解GFRP 筋芯复合桩(锚)的承载性能，建立计算理论模型具有重要意义。关于劲芯与水泥土界面之间的黏结强度，现有规范[2]还没有相应的推荐值或建议值。于宁等[8]通过水泥土中钢筋拔出试验发现，钢筋与水泥土界面的黏结强度随水泥掺入比提高呈线性增大趋势。顾士坦等[9]研究了芯桩(型钢)与水泥土界面剪应力的分布规律。陈昌富等[10-11]研究了GFRP 筋与水泥土界面的黏结滑移特性。目前尚未见掺纤维和建筑垃圾水泥土中GFRP筋的黏结性能研究成果。

目前，多借用钢筋-混凝土(砂浆)界面的黏结滑移模型[12-13]研究劲芯与水泥土界面的黏结性能，并且模型多采用分段式函数形式[14-16]，而能够较合理刻画纤维水泥土中GFRP筋肋效应的黏结滑移模型还未见文献报道。为此，本文作者首先采用均匀试验设计原理设计试验方案，开展淡水或海水养护环境下具有不同纤维和建筑垃圾掺量的水泥土中GFRP筋的拉拔试验和水泥土立方块无侧限抗压强度试验，得到GFRP 筋-水泥土界面的黏结滑移曲线；第二，通过试验得到的第一峰值黏结强度样本点建立Kriging 模型，据此对不同因素组合下的第一峰值黏结强度进行预测，并根据预测结果分析各因素对第一峰值黏结强度的影响；第三，由试验结果统计分析得到GFRP 筋-水泥土界面黏结滑移曲线的第一峰值点强度与水泥土无侧限抗压强度，与其余特征点(第一谷值点、第二峰值点、第二谷值点)强度的关系以及GFRP 筋肋距与各特征点位移之间的关系，基于黏结滑移曲线中4个特征点的强度和位移建立考虑肋效应的GFRP 筋-纤维水泥土界面黏结滑移模型；最后，根据水泥土的无侧限抗压强度和GFRP 筋的肋距间接建立GFRP筋-水泥土界面黏结滑移模型，并通过4组拉拔试验结果验证本文提出的2 种建模方法的可靠性。

1 基于均匀设计GFRP 筋-水泥土界面黏结性能试验

1.1 试验材料

试验所用的土采集于湖南省长沙市湘江江滩公园河漫滩，为淤泥质土，自然风干后粉碎过孔径为5 mm 的筛，液限为44.2，塑限为23.2，塑性指数为21.0。淤泥质土与建筑垃圾级配曲线见图1，试验材料见图2。水泥为P.O 42.5普通硅酸盐水泥。建筑垃圾(见图2(a))取自湖南云中再生科技股份有限公司，主要成分为破碎的混凝土。GFRP筋(见图2(b))来自山西诚鑫达矿山设备有限公司，直径d为16 mm，肋高约0.9 mm；每根GFRP筋的肋距各不相同，范围为9.8～10.2 mm，抗拉强度为622 MPa，剪切强度为116 MPa，弹性模量为40 GPa。玻璃纤维丝(见图2(c))长度为12 mm，抗拉强度大于210 MPa。

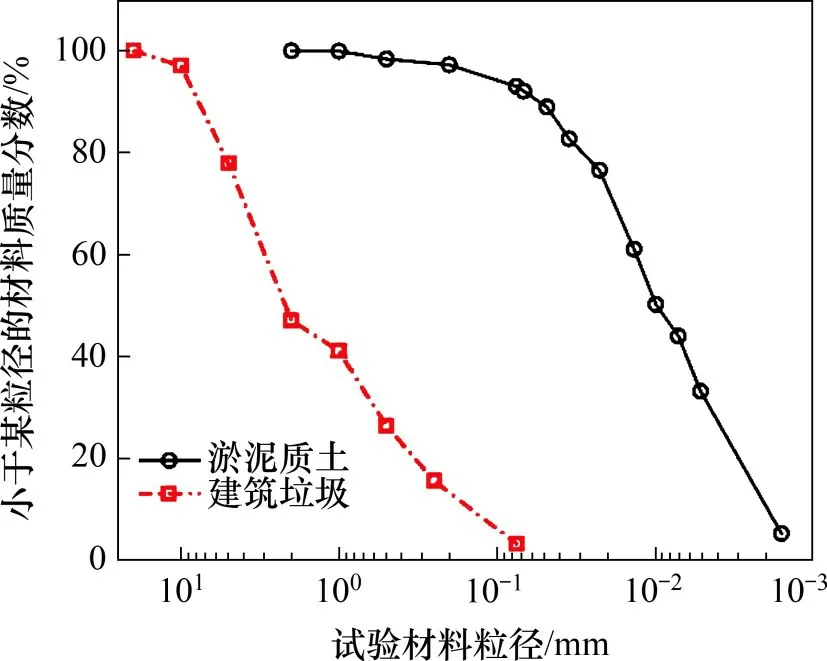
图1 淤泥质土与建筑垃圾级配曲线Fig.1 Particle grading curves of mucky soil sample and construction waste

图2 试验材料Fig.2 Test materials

1.2 基于均匀试验设计法确定试验方案

本试验考虑制样/养护环境、水泥掺入比(即水泥质量与湿土质量之比)aw、纤维掺入比(即纤维质量与干土质量之比)af、建筑垃圾掺入比(即建筑垃圾质量与湿土质量之比)ac共4 个因素，各因素分别取6 个水平。制样环境分为淡水制样、海水制样，养护环境分空气、密封、水环境，于是，制样/养护环境有6种组合。试验因素水平见表1，均匀设计试验表见表2。

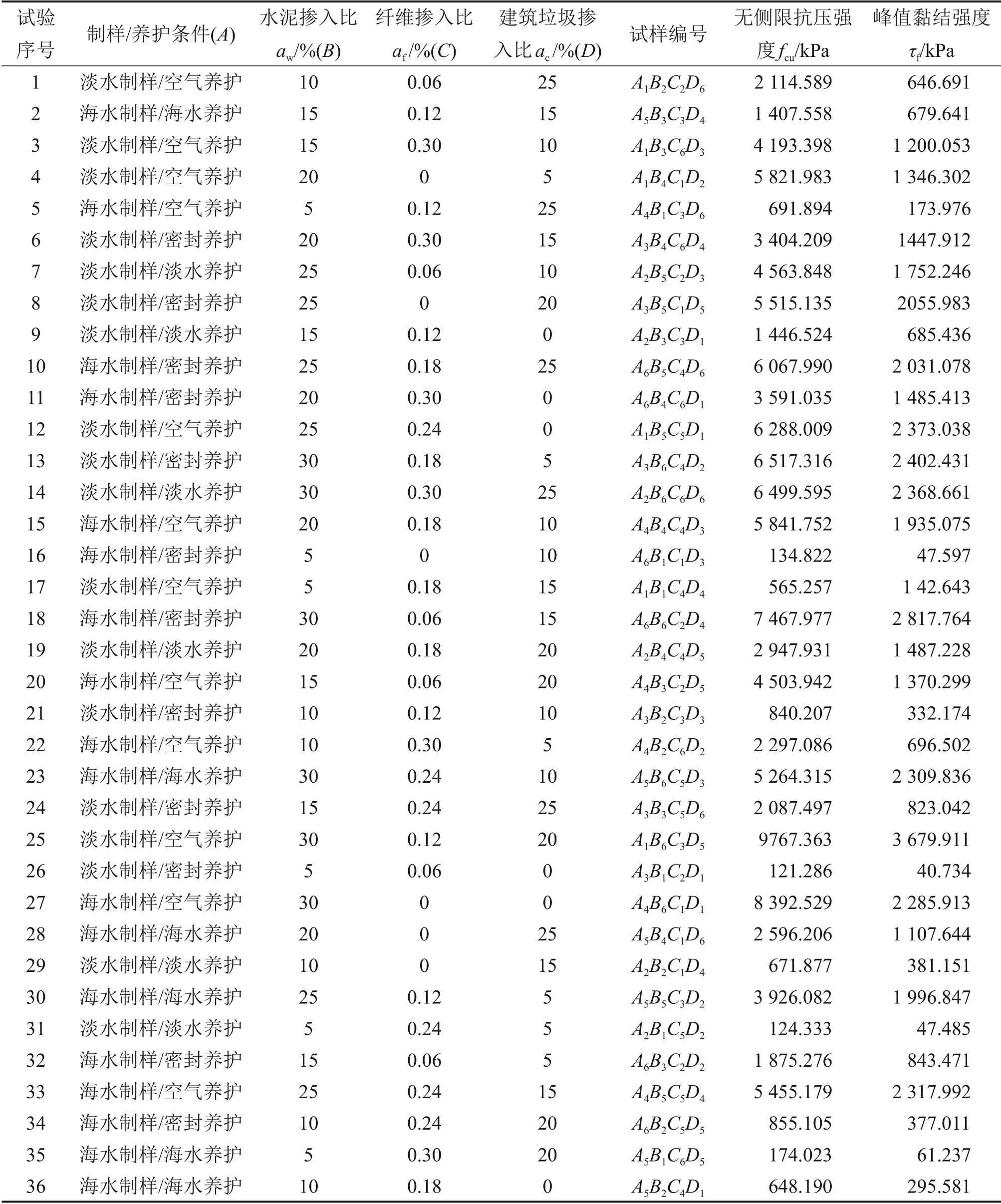
表2 均匀设计试验表Table 2 Uniform design experiment table

由于均匀试验设计法既能有效减少试验次数，又能保证试验点分布均匀，因此，本文基于均匀试验设计法设计了36 组试验，每组包括2 个平行的GFRP筋拉拔试样及3个水泥土立方块试样。

试样编号形式见图3。以试样编号A1B2C2D6为例，结合表1所示的试验因素及对应各因素水平，表示该试样是淡水制样/空气养护(A因素1 水平，A1)，水泥掺入比aw=10%(B因素2水平，B2)，纤维掺入比af=0.06%(C因素2 水平，C2)，建筑垃圾掺入比ac=25%(D因素6水平，D6)，其余类推。

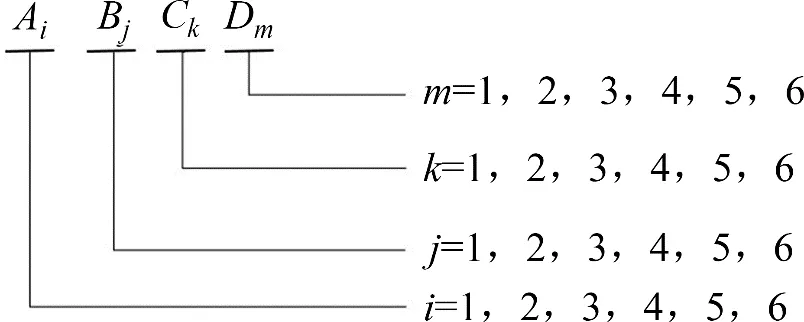
图3 试样编号示意图Fig.3 Schematic diagram of sample number

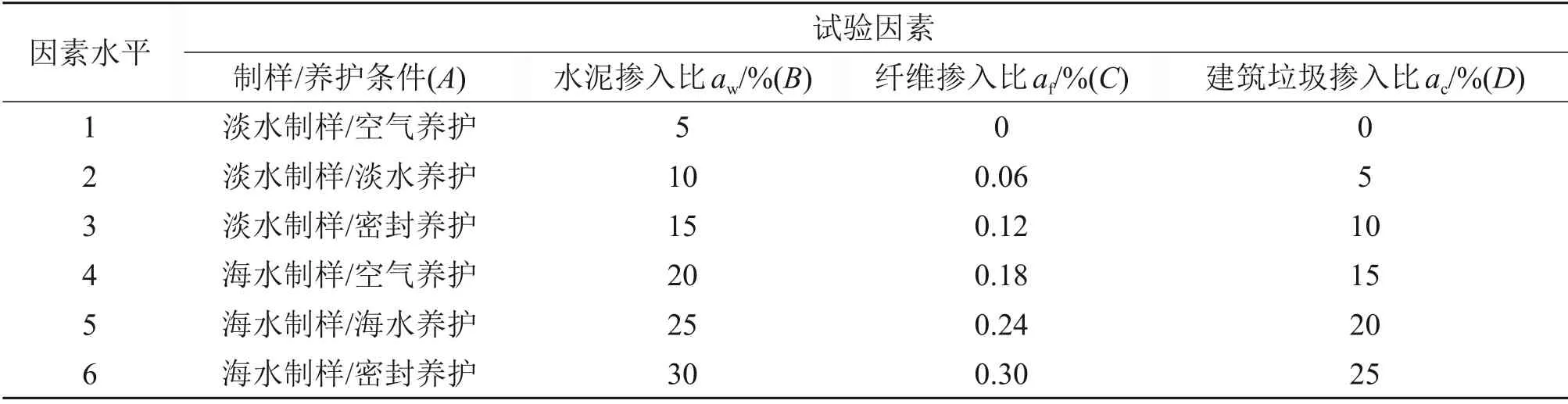
表1 均匀设计试验因素水平表Table 1 Uniform design experiment table

1.3 试样制备及测试

GFRP 筋拉拔试样为圆柱体，直径为192 mm，高为120 mm。GFRP筋正中插入试样，筋体包裹于水泥土中的长度，即黏结长度l=80 mm，水泥土立方块试样长×宽×高为70.7 mm×70.7 mm×70.7 mm。

1)模具准备。在拉拔试样模具及标准三联塑料砂浆试模内壁涂满凡士林以便于后期拆模，将GFRP筋插于拉拔试样模具正中位置，用胶带黏牢模具。

2)配比试验材料。按试验方案中的配比称量好土样、水泥、纤维、建筑垃圾和水，水泥土试样含水量(即水的质量与干土质量之比)取65%。

3)水泥土搅拌。将试验材料倒入搅拌桶中，干拌混合60 s，加水继续搅拌480 s至搅拌均匀。

4)装模成型。将水泥土迅速注入模具并振捣，使试样均匀、密实，试件浇筑完成后置于相应养护环境下固化，见图4(a)。

5)拆模及养护。制样完成后24 h 内拆模，按试验方案所述分别在空气、密封袋、淡水/海水环境(海水环境由海盐与水按质量比1:30制成)中继续养护至28 d，见图4(c)。

6)试件测试。使用万能试验机进行无侧限压缩试验和拉拔试验，以1 mm/min的速率拉拔(见图4(b))，拔出筋体长度为20 mm时停止试验[11]，试验结束后的试样见图4(d)和图4(e)。

1.4 拉拔试验结果

通过万能试验机进行拉拔试验可得到拉拔力F与筋体位移s关系。由于单元体试件尺寸远小于实际锚杆尺寸且试样与筋体黏结长度较小，可认为筋-水泥土界面上黏结应力竖向分布均匀，则黏结强度τ可按下式计算：

式中：F为拉拔力，N；d为GFRP 筋公称直径，mm；l为GFRP筋与纤维水泥土的黏结长度，mm。

因筋体强度较大，黏结滑移值可取万能试验机记录的GFRP筋顶部位移s。

本试验共对72 个试样进行拉拔试验，其中65个试件的筋体在拉拔作用下，与周围水泥土体的界面发生剪切滑移破坏，水泥土体保持完整，拉拔后的完整试样见图4(d)。6 个试件发生水泥土体劈裂破坏，GFRP筋与水泥土界面机械咬合力和黏结力骤降，不能准确反映界面的黏结性能，在后续试验数据回归分析时去掉。破坏后的试样见图4(e)。1个试件因在拉拔过程中存在操作失误而被废弃。对试验数据进行处理，可得到拉拔试样黏结强度与黏结滑移量的关系，见图5。从图5可见：大部分界面黏结滑曲线在峰值点后下降，随后又出现曲线波动式衰减的现象，少数曲线残余段未出现明显起伏。

图4 试验过程与筋体拉拔后水泥土体状态图片Fig.4 Pictures of test process and cemented soil state after bar pull-out experiment

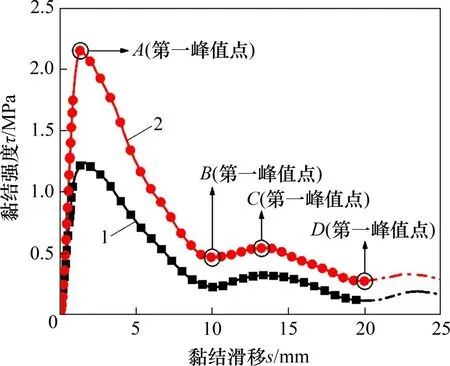
图5 具有肋效应的黏结滑移曲线Fig.5 Bond-slip curves with rib effect

2 基于拟合的Kriging 模型分析GFRP 筋-水泥土界面黏结强度影响因素

因试验采用均匀试验设计，仅由36 组试验无法直接得到各因素对GFRP 筋-纤维水泥土黏结强度的影响关系。Kriging 插值法是一种利用已知样本点线性加权系数差值预测变量空间内任一点函数值的无偏估计方法[17]。Kriging 模型作为一种估计方差最小的无偏估计模型，具有在小样本情况下拟合效果较好和预测非线性问题时精度较高且没有随机误差的优点，因此，使用Kriging 模型可根据部分因素组合下的峰值黏结强度试验点较可靠地预测不同试验因素组合的拉拔试验第一峰值黏结强度，从而克服因均匀试验设计造成试验数据点较少的不足。通过Kriging 模型预测得到不同试验因素组合下的拉拔试样第一峰值黏结强度后，对预测的第一峰值黏结强度进行分析，可得到当其他因素不变时，单一因素对峰值黏结强度的影响。

2.1 试样养护环境对第一峰值黏结强度的影响

整体上看，当其他条件相同时，海水制样的试样峰值黏结强度比淡水制样下界面峰值黏结强度高10%～70%，最高达到90%以上，其原因是采用水泥土制样时，加入海水会使水泥土水化反应增快，致使水化产物增大，并填充于水泥土孔隙，从而使水泥土强度增大[18]。

对养护条件而言，空气养护中试样峰值强度最大，密封环境与水环境对试样峰值强度影响较小。当水泥掺入比大于20%时，密封环境下试样峰值强度比水环境下的略大，见图6(a)。造成该影响的原因是空气环境相对于其他环境较干燥，而密封养护环境和水环境中的空气相对湿度较高，水泥土试样与环境交换水分子使水泥土中含水量增多，所形成的晶体结构少，使得水泥土在密封和水环境中养护的强度比在空气环境中养护更小[19]。

2.2 水泥掺入比对第一峰值黏结强度的影响

当其他条件一定时，在水泥掺入比为5%～30%时，第一峰值黏结强度随水泥掺入比增大而增大，涨幅为2 000～3 500 kPa，见图6(a)。

2.3 纤维掺入比对第一峰值黏结强度的影响

纤维掺入比对第一峰值黏结强度的影响与制样/养护条件有关。在淡水制样条件下，当其他条件一定时，峰值黏结强度随纤维掺入比增大呈先增大后减小的变化趋势，峰值黏结强度的极大值与极小值间的差值范围为20～650 kPa。但峰值黏结强度的极大值所对应的纤维掺入比略有不同：密封环境下，该值在0.18%左右；空气及水环境下，该值在0.24%左右，见图6(b)。造成该影响的原因是在水泥土中掺入一定量的玻璃纤维后，纤维与水泥土间产生黏结力，纤维之间相互交错形成空间网状结构，阻碍了试样内部裂缝的进一步扩张，水泥土强度增大。而当纤维掺量过大时，纤维间的间距变小，从而影响纤维与水泥土间黏结力的发挥，导致水泥土强度降低[6-7]。

在海水制样条件下，当水泥掺入比小于20%时，峰值黏结强度随纤维掺入比增大而增大；当水泥掺入比大于20%时，峰值黏结强度随纤维掺入比增大而略有减小，见图6(c)。其原因是海水制样时，碱性环境中大量的氢氧根易与土体中的镁离子、钙离子等结合生成沉淀和弱电解质等产物，这类产物加强了纤维与水泥土间的黏聚力与摩擦力，从而增强了水泥土强度。加入较大量玻璃纤维可能会导致部分纤维聚集成团，不能均匀分布于水泥土样中，达不到强度增强的效果，在被腐蚀后形成片状反而导致裂缝的产生和发展，使水泥土强度降低[20]。

2.4 建筑垃圾掺入比对第一峰值黏结强度的影响

建筑垃圾掺入比对第一峰值黏结强度的影响与制样条件有关。在淡水制样条件下，峰值黏结强度随建筑垃圾掺入比增大而增大，可增大1.4～2.0 倍，见图6(d)。其原因是建筑垃圾材料吸水性较高，促进水泥水化生成更多水化产物，水化产物之间相互联结使水泥土内部结构更加紧密[21]。

在海水制样条件下，峰值黏结强度随建筑垃圾掺入比增大呈先增大后减小的变化趋势，在建筑垃圾掺入比为15%～20%时到达峰值，见图6(e)。其原因是建筑垃圾材料在碱性环境中与水泥水化产物氢氧化钙发生化学反应，生成性能更优的低碱度水化产物以提高水泥土强度。然而，加入较多量的建筑垃圾会影响水化产物的联结作用，导致水泥土内部结构松散，使水泥土强度减弱[22]。

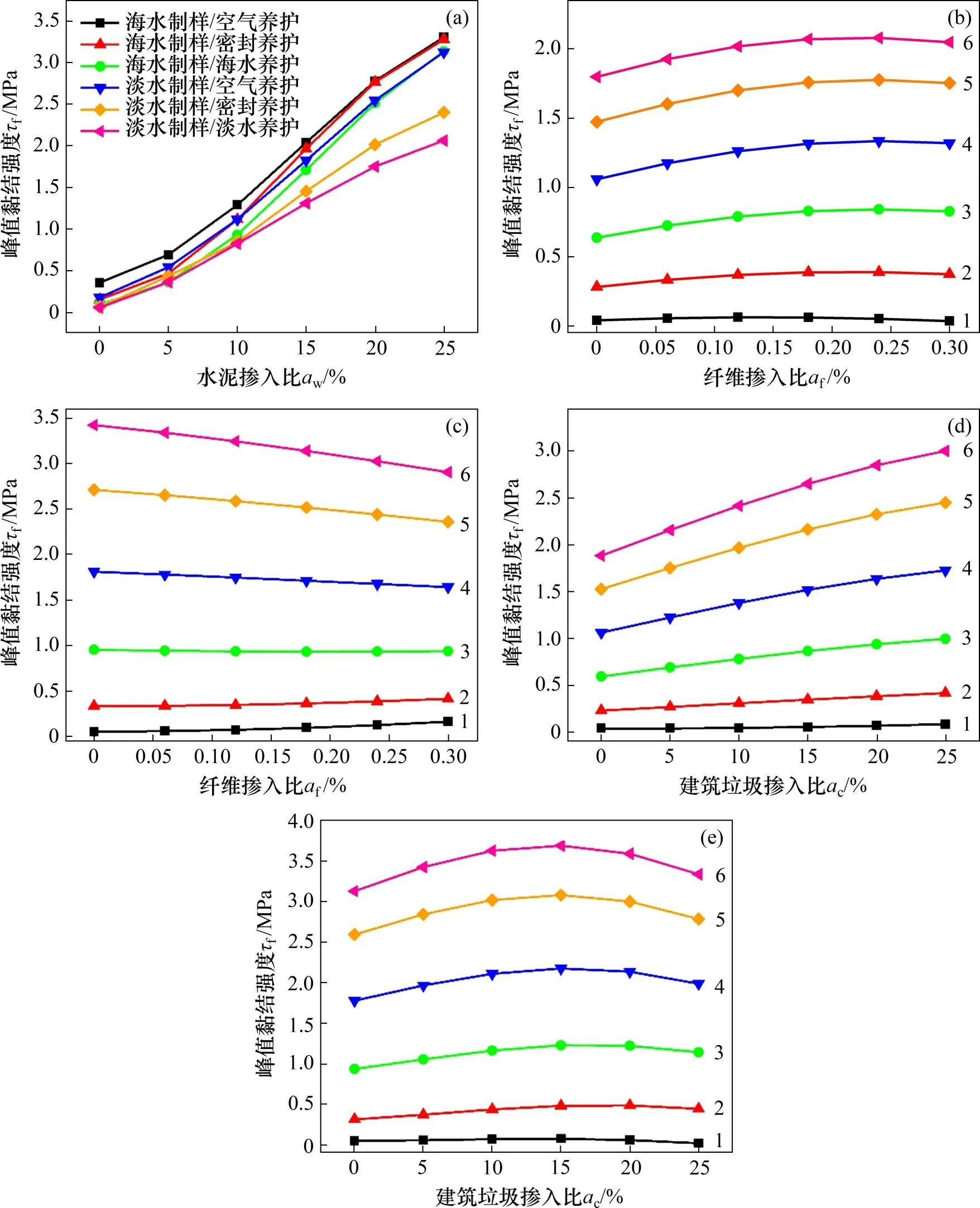
图6 各因素与Kriging模型预测峰值黏结强度的关系Fig.6 Relationship between experimental factors and ultimate bond strength predicted by Kriging model

3 GFRP 筋-水泥土界面黏结滑移特征分析

3.1 GFRP筋-水泥土界面黏结滑移曲线形态特征

由图5可见GFRP 筋-纤维水泥土黏结滑移曲线在峰值点后下降随后又出现波动式衰减。筋体带肋所导致的黏结滑移曲线软化段出现波动式衰减的现象称为“肋效应”。

具有肋效应的GFRP 筋-水泥土界面黏结滑移曲线见图7，可大致由第一峰值点A、第一谷值点B、第二峰值点C、第二谷值点D这4 个特征点将曲线划分为OA(弹性上升段)、AB(塑性软化段)、BC(残余上升段)、CD(残余下降段)和DE(残余延长段)共5个变化阶段，其形态特征可描述如下。

图7 具有肋效应黏结滑移曲线的形态特征Fig.7 Shape characteristics of bond-slip curves with rib effect

OA段：筋体受拉时肋凸起部分挤压周围水泥土，随着径向荷载增加，试件处于弹塑性变形阶段，滑移量快速增大，使得塑性区不断增大直至贯穿试件水泥土凸起形成破坏面时，拉拔荷载到达最大值，此时，曲线到达A点(黏结滑移量为sA，黏结强度为τf)。

AB段：GFRP 筋沿前期形成的破坏面运动，因水泥土被剪碎，肋前碎土堆积，界面摩擦力及机械咬合力减弱，黏结强度降低，此时，曲线到达B点(黏结滑移量为sB，黏结强度为τB)。

BC段：GFRP 筋继续运动与水泥土凸起发生剪切效应，致使竖向荷载增加，并再次形成水泥土破坏面，此时曲线到达C点(黏结滑移量为sC，黏结强度为τC)。

CD段：GFRP 筋沿再次形成的破坏面运动，界面摩擦力继续减弱，拉拔荷载继续下降，此时曲线到达D点(黏结滑移量为sD，黏结强度为τD)。随着黏结滑移量增大，黏结强度出现循环波动并持续衰减。

于是，黏结滑移曲线上A，B，C和D点的滑移量、黏结强度及其一阶导数为

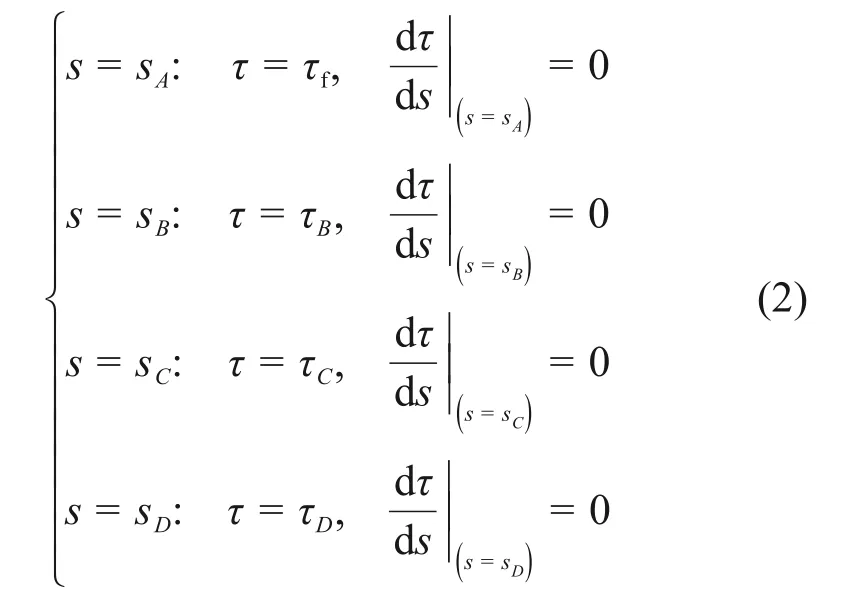
3.2 第一峰值点黏结强度与水泥土无侧限抗压强度间的关系

对试验点峰值黏结强度与无侧限抗压强度进行回归分析发现，拉拔试样GFRP 筋-水泥土界面峰值黏结强度τf与水泥土立方体无侧限抗压强度fcu呈线性相关，见图8，其拟合关系式如下，

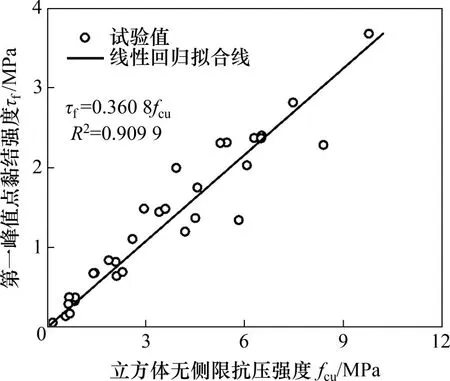
图8 第一峰值点黏结强度与无侧限抗压强度的关系Fig.8 Relationship between ultimate bond strength and unconfined compressive strength

拟合线性回归所得相关系数R2=0.909 9，说明线性关系较强，拟合效果好，试验结果可信。

3.3 第一峰值点黏结强度与其余各特征点黏结强度的关系

各特征点黏结强度与峰值黏结强度关系见图9。分析图9发现第一峰值点黏结强度与第一谷值点、第二峰值点、第二谷值点的黏结强度呈线性关系，其拟合关系式如下：

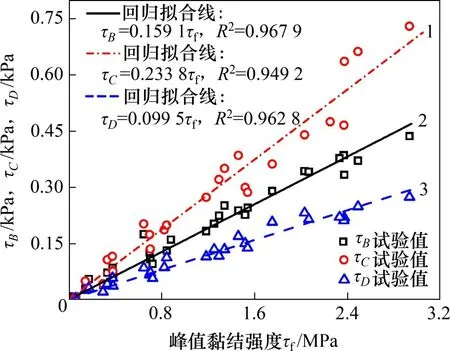
图9 各特征点黏结强度与峰值黏结强度的关系Fig.9 Relationship between bond strength of each characteristic point and ultimate bond strength

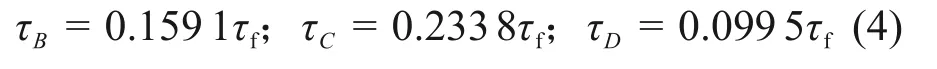
3.4 黏结滑移曲线各特征点位移与肋距间的关系

郝庆多等[23-24]发现带肋筋的肋间距对黏结性能(尤其是软化段)有明显影响。本文对71个有效试验中GFRP 筋的肋距ls与黏结滑移曲线特征点的滑移量s进行统计分析，发现特征点的滑移量与相应肋距具有相关性。为后面讨论方便，定义黏结滑移曲线上各特征点的黏结滑移值s与GFRP 筋的肋距ls之比为系数km(m为A，B，C和D)，有

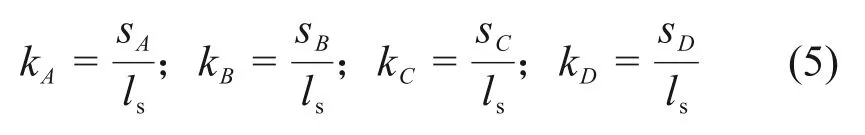
式中：kA，kB，kC和kD分别为第一峰值点A、第一谷值点B、第二峰值点C和第二谷值点D的滑移值(sA，sB，sC和sD)与肋距ls之比。

由试验结果统计分析可得各特征点处kA，kB，kC和kD的均值、标准差、变异系数以及正态分布概率为0.954 4(2σ原则)时的km的分布区间，见表3。根据kA，kB和kC的建议值和式(5)，可由GFRP筋肋距较准确地预测出特征点A，B和C对应的滑移量。

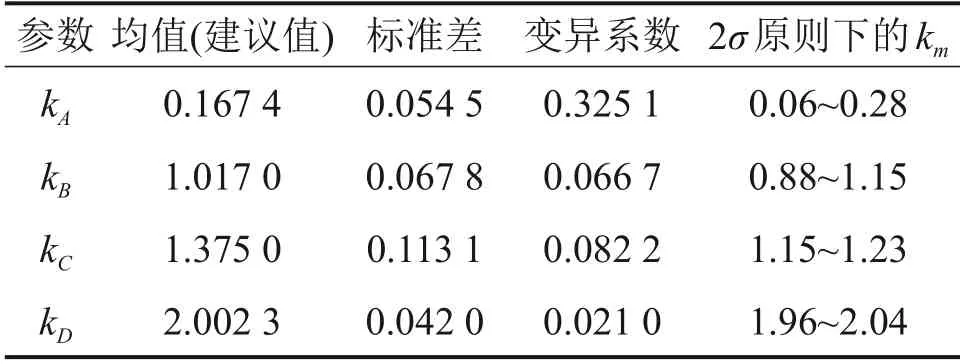
表3 黏结滑移曲线特征点kA，kB，kC和kD建议值Table 3 Suggested value of characteristic points kA，kB，kC and kD of bond-slip curve

通过对sD统计发现，sD的平均值为20.05 mm，kD变异系数为0.021 0，远小于其他参数(kA，kB和kC)的变异系数，说明sD离散性较小且大部分曲线的sD略大于20 mm。试验结束时(筋体拔出位移为20 mm)，sD略大于20 mm 的曲线还未到达第二谷值点，对后文建模造成不便，故在此进行近似处理，在黏结滑移模型建立中统一将第二谷值点的滑移量sD固定为20 mm。

4 考虑肋效应GFRP 筋-水泥土界面的黏结滑移模型

由现有研究可知，带肋筋-水泥土/混凝土界面拉拔试验黏结滑移曲线均存在残余段起伏的特征，曲线呈波浪式逐渐衰减至某一稳定强度[25]，即“肋效应”对于黏结滑移曲线的影响不可忽略。已有的黏结滑移模型中，有的分段描述黏结滑移曲线特征，形式复杂，不便应用；有的对曲线弹性上升段或塑性软化下降段线性简化，将具有明显衰减波形(即肋效应)的残余段简化为某一恒定值，但不能准确地反映实际试验曲线变化过程。

因此，为考虑GFRP 筋拉拔试验中的肋效应，本文据式(6)拟合GFRP 筋-掺建筑垃圾和纤维水泥界面黏结滑移曲线：

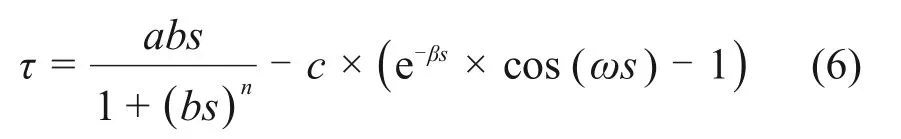
其中：τ为黏结强度；s为黏结滑移；a，b，n，c，β和ω未知参数。该模型有如下特点：当s=0 时，

将特征点A，B，C和D的黏结位移sA，sB，sC和sD以及黏结强度τf，τB，τC和τD代入式(6)和方程组(2)，利用最小二乘法迭代求出式(2)的最优未知参数解，再将参数代入式(6)，即可得到对应试件的完整τ-s拟合曲线模型。

对试验所获得的所有黏结滑移曲线进行模型拟合，可以发现模型曲线与真实试验曲线重合程度都较高，能较准确地刻画黏结滑移曲线弹性上升段和由“肋效应”引起的残余波动段特征。因此，仅通过黏结滑移曲线上4 个特征点的黏结强度、位移来拟合完整黏结滑移曲线的方法是可行的。4组拉拔试样的黏结强度与黏结滑移试验数据点与模型拟合曲线对比见图10。

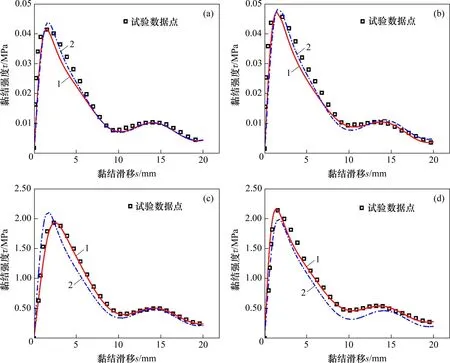
图10 试验数据点与拟合函数曲线、预测曲线对比图Fig.10 Comparison of test data points and fitted function curves&prediction function curves

5 基于水泥土无侧限抗压强度fcu建立黏结滑移曲线预测模型

由以上分析可知，只要通过拉拔试验获得GFRP 筋-水泥土的黏结滑移曲线，就可根据曲线中4个特征点的强度和位移建立完整的黏结滑移模型。由于式(3)和(4)建立了各特征点的强度与水泥土的立方块无侧限抗压强度fcu之间的关系，式(5)和表3建立了各特征点的位移与肋距ls之间的关系，因此，只要测得水泥土立方块抗压强度fcu和GFRP 筋肋距ls，就可以在未做拉拔试验的情况下建立GFRP 筋-水泥土的黏结滑移模型。建模步骤如下。

1)开展淡水/海水养护环境下具有不同纤维和建筑垃圾掺量的水泥土无侧限抗压强度试验，得到水泥土无侧限抗压强度fcu，测定GFRP 筋的肋距ls。

2)将无侧限抗压强度fcu代入式(3)，得到与其养护环境和配方相同的拉拔试验的第一峰值黏结强度预测值τf，再将τf代入式(4)得到各特征点黏结强度的预测值τB，τC和τD。

3)将GFRP筋的肋距ls和表3中提供的kA，kB和kC的建议值代入式(5)，得到各特征点黏结滑移预测值sA，sB，sC和sD。

4)联立式(6)和式(2)，将步骤2)和3)得到的各特征点的黏结强度预测值(τf，τB，τC)和(τD)以及黏结滑移预测值(sA，sB，sC和sD)代入式(2)和(6)，求解未知参数a，b，n，c，β和ω。

5)将求解得到的参数a，b，n，c，β和ω代入式(6)得到考虑肋效应的黏结滑移预测模型。

为验证上述建模方法的可靠性，选取4组未参与式(3)和式(4)、表3统计规律建立的试验数据，根据其无侧限抗压强度fcu、肋距ls，按上述方法预测了黏结滑移曲线，见图10。由图10可见：黏结强度-滑移值的预测结果与试验结果较接近，说明预测效果良好，预测方法可行。