基于EEMD-MPE-LSSVM 的光伏发电功率预测
2021-10-23朱瑞金龚雪娇张娟娟
朱瑞金,龚雪娇,张娟娟
(西藏农牧学院电气工程学院,西藏 林芝 860000)
0 引 言
光伏发电作为可再生清洁能源在电力系统中占比越来越大,由于光伏发电功率受到太阳辐射角、温度、湿度等不确定因素的影响,造成输出功率随机性强,给光伏并网带来了调度困难、安全性低等问题[1-2]。为保障电网安全稳定运行,现主要采用拉闸限电等维护策略[3],存在着耗能大,不利于光伏发电的继续发展。近年来,国内外研究者为实现常规能源与光伏发电之间的合理调度,提出了一系列对光伏发电功率提前预测算法[4-6],以适应其输出功率对电网系统的影响。
光伏发电功率预测主要分为间接预测和直接预测两种方式。间接预测方法是根据光伏发电输入条件构造信息特征来进行预测,如光照强度、太阳辐射强度、风速、温度、天气状态等外部条件。徐先峰等[7]提出利用双向长短期记忆(BiLSTM)算法,充分挖掘气象数据以实现光伏发电功率的短期预测,将光伏发电历史功率曲线下的气象条件与当前气象数据进行曲线拟合时,考虑到气象条件的随机性,存在可靠性和信号特性相关性低等问题。王志忠等[8]根据晴朗系数构建基于相似日输出功率的ARIMA 预测模型,以单纯的晴朗系数作为输入特性时,存在信号特征单一和样本集要求高等问题。
直接预测方式是将历史发电输出功率作为研究对象建立功率预测模型。候松宝等[9]提出利用主成分分析和BP 神经网络进行短期光伏发电功率短期预测,由于受天气状况影响,当外部条件变化时,功率预测精度和稳定性将会下降。李攀等[10]利用稀疏贝叶斯学习算法,对输出功率的影响因素进行权重分析,建立观测器模型对输出功率进行回归分析。
基于以上分析,本文提出将间接预测法和直接预测法相结合的EEMD-MPE-LSSVM 光伏发电功率预测算法,使输入条件参与输出功率预测,提高了预测的准确度。采用直接预测方法以光伏发电输出功率为研究对象,EEMD-LSSVM 预测方法结合迭代误差完成功率预测;考虑到间接预测方法中天气因素的影响,将不同天气类型进行信号复杂度量化分析,采用MPE 构建输入特征向量,并参与到LSSVM 曲线预测中。通过现场数据进行实例验证,该算法提高了预测精度,具有一定适用性。
1 光伏发电系统输出功率特性
光伏发电系统输出功率具有非线性、不平稳特性,影响因素除天气类型以外,还考虑到气象条件使得输出功率随机性增加。本文参照中国气象局制定的GB/T 22164—2008 对33种天气类型进行模糊分类,将相似度较高的天气类型归为一类,经分类后的天气主要有晴天、雨雪、多云和突变天气4种类型。
在4种不同天气类型下进行输出功率统计,图1为某光伏发电站从06:00-20:00,每15 min 采集一次光伏发电输出功率的曲线,其纵坐标为光伏发电输出功率。

图1 不同天气类型下光伏发电输出功率曲线
从图1 中可以看出:阴天下受到太阳辐射最小,输出功率也随之减少;晴天下的发电功率稳定;遇到突变天气,发电功率呈现不稳定现象;雨雪天气下较晴天发电功率下降。在连续时间序列下,用排列熵对不同天气类型进行量化,并作为SSVM 的输入向量的一部分提高预测精度。
2 功率预测算法分析
2.1 集成经验模态分解(EEMD)
EEMD 分解方式是在经验模态分解(EMD)基础上提出的,EMD 算法对信号序列进行分解时,每个模态函数(instrinsic mode function,IFM)必须满足两个条件[11]:
1)极值点和过零点的个数误差不超过1。
2)上下包络线的均值接近0。
为充分表征原始信号序列的频率特性,当剩余分量rn(t)为单调信号或没有足够极值点时结束迭代。以x(t)为原始信号序列,EMD 分解如下式所示:

考虑到当信号序列极值点不足时,EMD 分解存在模态混叠的问题,即一种模态分量可能存在不同频率特性。为此提出EEMD 分解方式,在分解之前加入n组均值为零的高斯白噪声hi(t),如下式所示:

再对每组信号进行EMD 分解:

式中:Cij(t)——第i组模态分解;
ri(t)——第i组剩余分量;
j——分解层数。
最后根据高斯白噪声均值为零的特性,对i组模态分量进行求均值处理,即:

EEMD 分解中Cj(t)代替式(1)中IFMi(t)模态分量,成为新的模态分量。
2.2 多尺度排列熵(MPE)
为表征不同信号序列的复杂度,引入MPE 算法计算熵值,从而实现复杂度的量化目标。在熵值计算之前,需要对原始信号序列X={x(i)|i=1,2,···,n}进行相空间重构,假设时延参数等于τ,嵌入维度等于m,则重构矩阵为:

其中j=1,2,···,K;K=n–(m–1)τ
对重构矩阵中每一行进行降序或升序排列,计算每种排序方式在m!种排序中的概率分布P1,P2,···,PK,按照下式计算其多尺度排列熵,并进行归一化处理:

由熵值定义可知:熵值越大,表示信号序列越复杂。
2.3 最小二乘支持向量机(LSSVM)
支持向量机(SVM)算法引用最小二乘损失函数,将最优问题转换为线性方程,从而实现样本数据的预测[12]。具体算法步骤如下所示:
1)构造目标函数:对于线性不可分问题,加入核函数φ (xi)和惩罚因子c。

式中:y——故障类别标签,即yi∈[–1,1];
ξ——误差分量。
2)利用拉格朗日函数,对目标函数进行求解,当拉格朗日乘子等于αi时,优化问题表述为:

3)利用KKT 条件对式(9)进行求解,最后求得回归函数为:

LSSVM 具有小样本、自适应预测的优势,采用径向基函数进行线性化处理,减少了输入参数,提高了运算速度。
3 光伏发电功率预测流程
本文采用EEMD-MPE-LSSVM 模型进行光伏发电功率预测。在实际应用中受到气象条件的影响,首先用排列熵表征对天气类型进行量化;然后利用EEMD 分解方式提取细节分量,并对分量回归预测后进行重构;最后计算初始训练样本迭代误差序列,从而实现发电功率的整体预测。具体算法流程如图2 所示。

图2 EEMD-MPE-LSSVM 光伏发电功率预测流程图
1)考虑到同一天有可能存在不同天气状况,选择4 个天气类型相似的临近日发电功率计算排列熵,并作为LSSVM 输入特征向量。
2)当构造初始迭代误差序列时,在历史数据中选择q个数据作为训练样本集,以第a个数据点为起点,利用滚动时间窗口预测方法得到q–a个功率预测值。在与真实值比较后得到预测的一级误差,并重复上述步骤,最终获取x(e1)~x(ep)为1 级~p级误差序列。在实际应用中参考文献[13],p一般不超过3。
3)EEMD 分解结合排列熵特征对每一模态函数IFM 进行LSSVM 预测,将重构后的预测结果加入迭代误差序列得到最终预测值。
4 实验部分
4.1 不同天气类型的排列熵计算
本文选用某装机容量为50 MW 光伏发电站实验数据来源,随意抽取4种不同天气类型,并通过临近日发电功率计算排列熵如表1 所示。

表1 不同天气类型下的排列熵
4.2 初始训练样本功率序列EEMD 分解
光伏发电输出功率受到多个不确定因素的影响,以发电系统前20 天历史数据为训练集,画出相应发电功率曲线图。由于输出功率呈现非线性、不平稳特征,为充分表征曲线特性,采用EEMD 分解方式将原始曲线分解成具有不同频率特性的模态函数分量IFM1~IFM4,图3 为20 天内光伏发电功率曲线及EEMD 分解结果。
由图3 可知,IFM4 符合没有足够极值点的EEMD分解终止条件。每个模态函数分量在保持功率曲线特性同时,降低了LSSVM 计算复杂度,提高了计算精度。

图3 训练集样本发电功率EEMD 分解结果
4.3 EEMD-MPE-LSSVM 功率预测结果
光伏发电功率受到太阳辐射角、气象条件、风速、湿度、温度等多个条件的影响,因此为预测特定时刻t的发电功率,以模态分量结合不同天气类型排列熵作为预测特征集进行样本训练。分别将预测之后的IFM1、IFM2、IFM3、IFM4 进行重构,并记为y1。然后将初始迭代误差x(e1)、x(e2)、x(e3)加入初始预测值y1。最后,最终t时刻的光伏发电功率预测值为y=y1+e1+e2+e3。
为验证该预测模型的有效性,本文选择春、夏、秋、冬4 个季节的4种不同天气类型共计16种发电功率进行预测。以春季晴天为例,分别在EEMDLSSVM 和EEMD-MPE-LSSVM 两种算法下进行光伏发电预测,经样本训练后的预测值与真实值分布如图4 所示。
通过对图4 中(a)和(b)的对比,EEMD-MPELSSVM 功率预测模型在相似日的基础上,量化了气象条件,并作为有效特征加入预测,提高了预测模型的精度。本文统计了对光伏发电功率50 天内的预测值和有效值,分别在EEMD-LSSVM 和EEMDMPE-LSSVM 两种不同的算法下评估其平均相对误差(MRE)和均方根误差(RMES),结果如表2 所示。从表中可知在用MPE 量化天气因素后,其预测结果的MRE 和RMES 分别为1.56%、3.14%,均低于EEMD-LSSVM 预测误差。
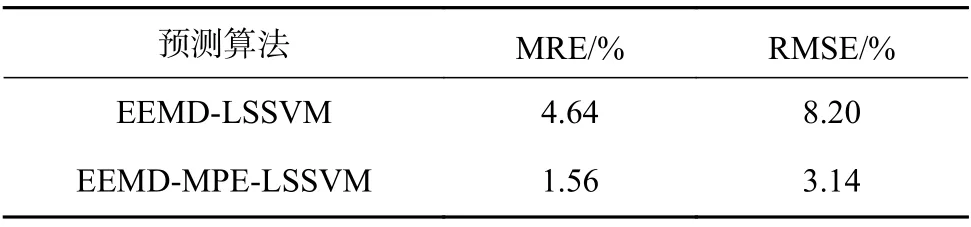
表2 50 天内预测误差

图4 春季晴天光伏发电功率预测结果
考虑到天气状况、太阳辐射角、温度、湿度、气象条件等不确定因素的影响,利用多尺度排列熵量化天气类型,并作为输入特征向量细化了LSSVM预测,证明了该算法的有效性。
5 结束语
本文针对光伏发电功率曲线特性,提出了结合天气因素的EEMD-MPE-LSSVM 光伏发电预测算法,通过实验论证得出以下结论:
1)光伏发电功率曲线数据进行EEMD 分解,通过提取出曲线细节分量,充分表征了功率曲线的局部特征,使得LSSVM 预测算法更加精准。
2)MPE 用于衡量天气因素的复杂度,同时参与到光伏发电功率预测中,进一步提高预测精度,并提供有效的细节分量。
3)光伏发电功率曲线具有随机性、非线性、不平稳等特性,通过迭代误差修正发电功率预测值。
本文提出的光伏发电预测模型兼顾不同天气类型的影响,经小样本训练后,能够对光伏发电功率实现准确预测。为实现光伏并网的合理调度和安全运行,提供了可行性参考方案。
