离散元聚苯乙烯颗粒细观参数辨识

庞绍锐，杨丽红，王双园

(上海理工大学机械工程学院，上海 200000)

0 引 言

真空担架由聚氯乙烯（PVC）软膜热熔后经密封形成腔体，内部填充变形量大，密度小的聚苯乙烯(EPS)颗粒。腔体被抽真空时，腔体内的EPS 颗粒会发生流动并转变成“类固体”状态[1]，随之产生可变的刚度[2]。由于人体各部分最大承受压力不同，通过研究颗粒与软膜抽真空过程的力学特性，可以研制不同结构的腔体，以便担架抽真空后可以更适合包裹和固定人体。离散元法（discete element method）是一种基于分子动力学的颗粒物料分析方法[3]，通过使用离散元软件EDEM 与多体动力学仿真软件Recurdyn 耦合，可以分析腔体压缩颗粒后的结构变化特征，为担架设计提供参考依据。由于颗粒的细观参数直接影响着宏观的力学特性变化，准确的离散元参数是仿真模拟的基础，仿真之前需辨识出EPS 颗粒与PVC 软膜的细观参数。

一般离散元理论主要研究对象为岩石、沙土、混泥土等[4]，对于颗粒的的细观参数测定，国内外学者基于离散元方法对土壤、粮食之类颗粒物质进行了大量的研究。GONVIA[5]采取休止角为模拟指标发现，采用具有摩擦等特性的离散元能很好地增加颗粒模拟效果，颗粒物质的细观参数对其宏观运动有着直接影响。以宏观休止角为响应值，韩燕龙[6]通过对休止角的仿真，对稻谷之间的滚动摩擦系数进行了仿真标定。王美美[7]等通过使用响应面优化方法对玉米籽粒进行离散元参数标定，提出多因数对响应休止角的最优参数标定。针对于颗粒的参数组合对休止角的影响，张锐等[8]使用EDEM 软件对颗粒之间相互作用参数进行标定，提出一种系统标定沙土颗粒相互作用参数的方法，颗粒的细观参数组合直接影响着堆积的休止角值。贾富国[9]等人利用离散元方法对稻谷颗粒堆积的休止角进行预测稻谷的细观参数。目前很多类型的颗粒测定采用经验值，这种方法往往导致实验数据不准确，研究结果的误差较大。EPS 颗粒相比于常见的沙土、岩石、粮食等物质特性更加特殊，需寻找一种不同的测定方法，且在研究颗粒散体动态加载的过程时，理想化使用有限元方法研究EPS 颗粒会忽略颗粒的不连续性[10]，造成散体运动研究的不准确性。

结合前文所述的相关研究，本文以EPS 颗粒与PVC 软膜为对象，设计一套方案来测定辨识EPS颗粒之间，EPS 颗粒与PVC 膜间的细观接触参数。研究基于Hertz-Mindlin 接触模型，以多种试验和仿真模拟结合的方法对颗粒进行离散元参数的测定，旨在为仿真研究颗粒在真空压缩过程产生的力学机理提供准确的接触参数。

1 离散元模型

1.1 颗粒模型

真空担架填充的EPS 颗粒，颗粒外观为球形，通过对颗粒进行网格筛选可知：粒径在3～3.5 mm占总量的20.5%，3.5～4 mm 占总量的21.7%，4～4.5 mm 为35.6%，4.5～5 mm 为22.2%。颗粒模型选择EDEM 软件内置的球形颗粒模型如图1 所示。在仿真时，将整个粒径分布分为4 个粒径段，可认为每个粒径段均匀分布，在仿真时以粒径3.25 mm、3.75 mm、4.25 mm、4.75 mm 作为颗粒的直径，分别按照所属粒径段的比例进行颗粒工厂设置。

图1 EPS 颗粒模型

1.2 颗粒接触模型

EPS 颗粒之间没有粘结，且颗粒接触面很小，在接触面上仅发生弹性变形。EPS 颗粒的运动是法向力与切向力耦合的一个状态[11]，很难得到两个接触颗粒的法向力和切向力分析解。因此，EPS 颗粒仿真分析时采用EDEM 内置的Hertz-Mindlin(no slip)接触模型来描述。EPS 颗粒接触模型如图2 所示，该模型将颗粒之间的法向和切向接触力简化成为弹簧和阻尼器的并联。法向力的计算采用Hertz 接触理论计算，切向力与切向位移关系采用Mindlin 接触理论[11]。

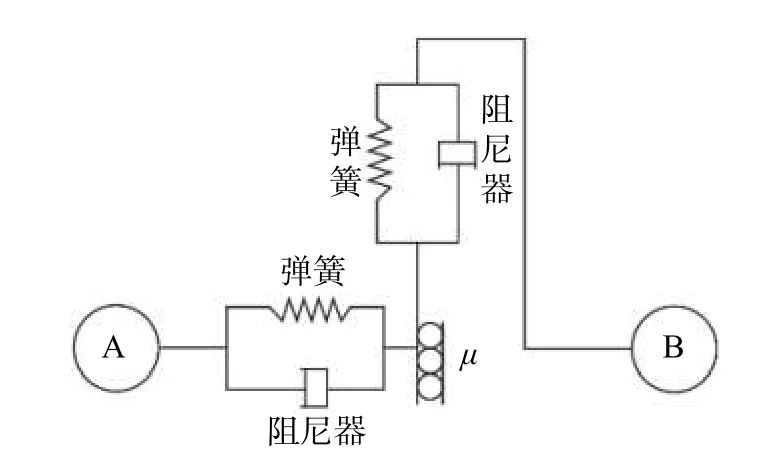
图2 接触力学模型

在EPS 颗粒发生运动时，颗粒之间碰撞挤压产生的法向力N为

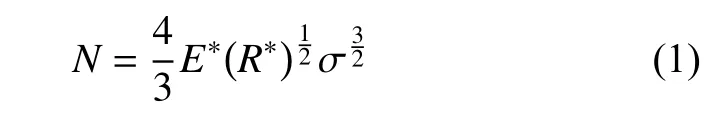
式中：σ——法向重叠量；

R∗——有效颗粒半径；

E∗——有效弹性模量。

其中R∗、E∗计算公式为

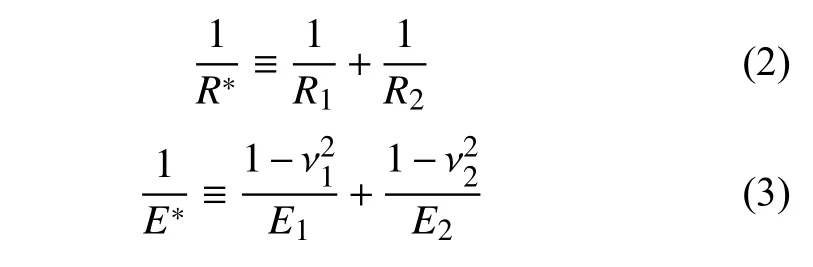
式中：E1、E2——颗粒1 和颗粒2 的弹性模量；

ν1、ν2——颗粒2 和颗粒2 泊松比。

当两颗粒间重叠量为 ∆σ 时，法向力增量 ∆N由式(1)可得

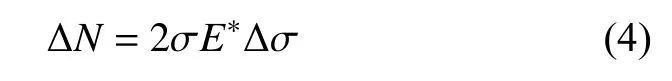
两接触面表面切向位移δ 时，切向力为T

其中Sτ为切向刚度。

在接触表面产生 ∆δ的切向位移增量，两者之间切向力增量 ∆T为

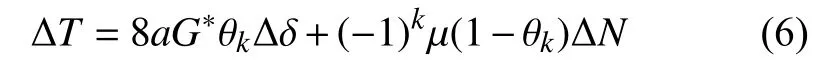
式中：µ——颗粒表面静摩擦因数；

G∗——有效剪切模量；

a——接触半径；

k=0，1，2——对应切向力的加载，卸载和卸载后重新加载，当

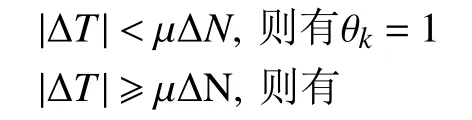
颗粒和颗粒，颗粒和PVC 软膜之间法向阻尼力Fnd和 切向阻尼力Fτd满足

式中：m∗——等效质量；

vτrel——切向相对速度；

vnrel——法向相对速度；

Sn——法向刚度，N/mm；

ε——恢复系数；

β——阻尼比。

颗粒之间存在的滚动运动，该运动主要通过接触表面滚动摩擦力矩Ti和 切向力矩Tτ决定。

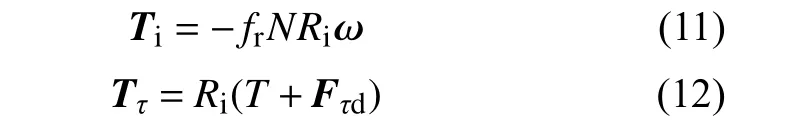
式中：fr——颗粒之间的滚动摩擦因数；

Ri——接触点到质心的距离；

ω——颗粒在接触点处的角速度。

2 接触参数的测定

离散元的部分接触参数在误差允许范围内可通过物理实验测量，为提高参数的准确性，利用离散元软件EDEM 进行仿真模拟和实验相结合来测定参数。所需的EPS 颗粒PVC 软膜本征参数[12-13]如表1 所示。

表1 本征参数

2.1 EPS 颗粒与PVC 软膜碰撞恢复参数测定

碰撞恢复系数是表现一个物体在受到碰撞时变形恢复的能力，在速度和冲量定义方法中，恢复系数定义为两物体碰撞前后在接触点相对分离速度与相对接近速度之比，理论计算公式为

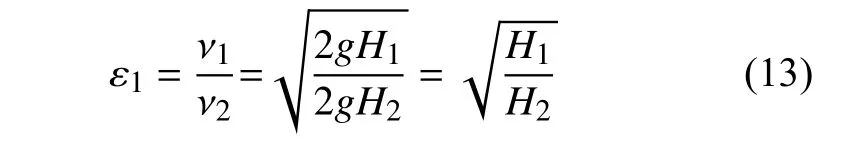
式中：H1——反弹之后的最大高度；

H2——初始颗粒降落高度。

相关研究表明，颗粒在下落实验测恢复系数时，下落高度影响着碰撞能量损失，恢复系数测定偏小[14]。为减小测定 ε1时能量损失带来的误差，如图3（a）选择将EPS 颗粒从高度H2=10 cm 处进行自由落体，与实验台上平铺的PVC 软膜进行碰撞。通过高速摄像机记录颗粒最高的弹起高度H1，实验进行六次，计算平均值，得到反弹起的高度实验均值为H1=2.55 cm。

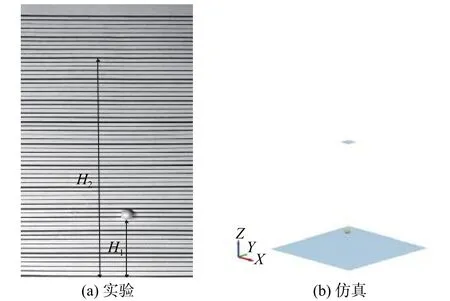
图3 碰撞恢复系数

以实验值为依据进行多次如图3（b）仿真实验,设置颗粒不同的碰撞恢复系数，得到颗粒反弹之后的轨迹，实验结果如图4 所示，可以看出随着EPS颗粒与PVC 软膜之间恢复系数 ε1降低，EPS 颗粒的初次反弹高度H1逐渐减小。

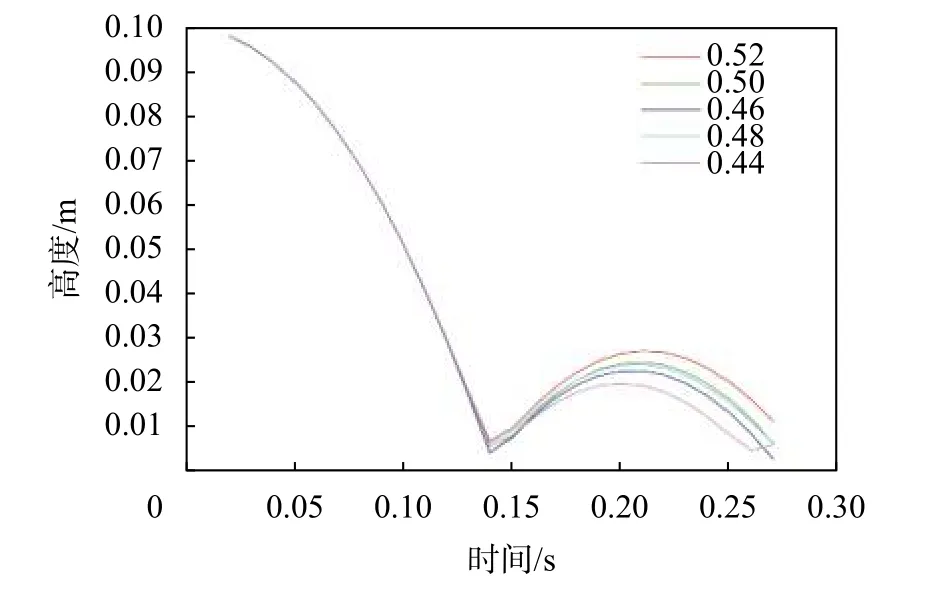
图4 颗粒降落位置曲线

根据实验的数据，设计仿真弹跳实验，以弹性恢复系数 ε1为 变量，ε1范围选择0.44～0.52，步长为0.02。每组进行三次仿真，以反弹高度H1平均值为结果，仿真实验的结果拟合方程为

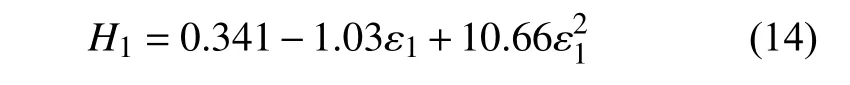
决定系数r2=0.998，该值接近1 表明拟合可靠度高。将实验测量值2.55 cm 代入式（14）中，得到弹性恢复系数 ε1=0.506，由公式（14）验证可得颗粒反弹的预测高度为2.56 cm，与实验的误差为0.38%，误差极小，则可确定仿真参数 ε1=0.506。

2.2 EPS 颗粒与PVC 软膜静摩擦因数测定

使用斜面滑测定EPS 颗粒与PVC 软膜之间的静摩擦系数 µ1时，颗粒的重力在斜面上分解为平行于斜面的力F1和 垂直于斜板的力F2，颗粒与软膜之间的静止摩擦力为f。当斜面的倾角 α大于静摩擦临界角的时候，F1>f时发生滑移，此时通过公式(15)可计算µ1

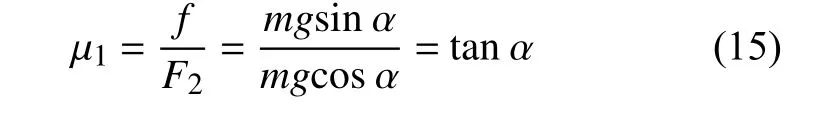
在实验与仿真的时候采取多颗粒粘结成块的方式，并将其放置在软膜表面如图5（a）。实验与仿真时，斜面旋转速度一致保持为0 .05 rad/s，仿真中斜面倾角通过时间乘以转速来计算。设置仿真时间步长为Rayleigh（TR）时间的8%，设置采集点间隔为0.001 s，可以精确采集每个点颗粒板的运动状态并计算斜面角度α。

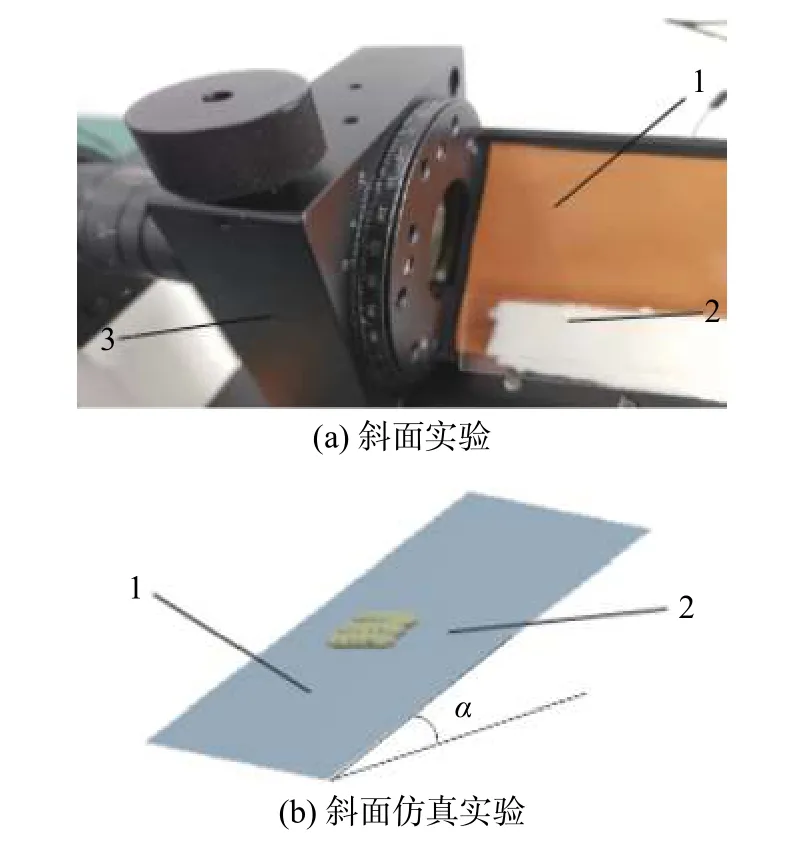
图5 EPS 颗粒和PVC 表面静摩擦实验

进行斜面实验时，当颗粒板块发生滑动，记录此时斜面倾斜角，重复测量5 次之后，取平均值为42.15°。在EDEM 仿真软件Creator 界面下创建New Section (0.06 m×0.06 m)来模拟角测量仪斜面上的PVC 软膜，仿真过程中改变颗粒与PVC 软膜接触的静摩擦因数，进行6 组仿真实验，记录每组仿真实验滑动斜角，实验结果如表2 所示。

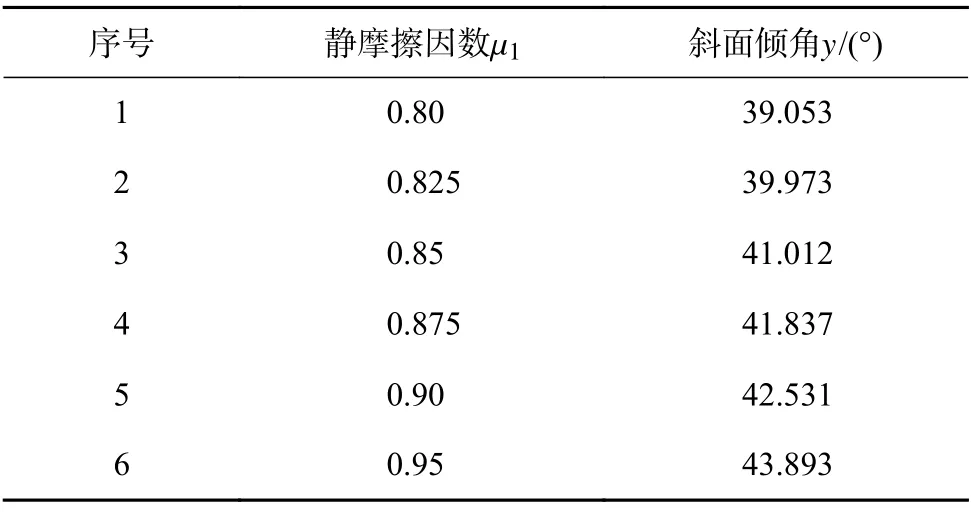
表2 µ 1选取与倾角结果

对仿真实验中的数据进行曲线拟合，得到 µ1与y的二次多项式如图6 所示，曲线方程为：

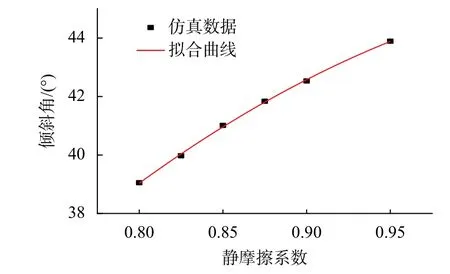
图6 静摩擦系数与倾斜角拟合曲线

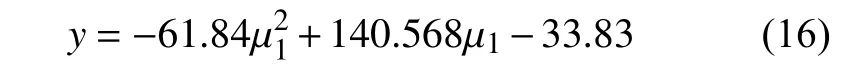
该方程式的决定系数为r2=0.99891，接近1，表明此拟合多项式极其符合EPS 颗粒斜面实验的系数与摩擦因数之间的关系。将室内斜面实验所得到的平均值42.15°代入方程可得 µ1=0.885。由公式(15)可得静摩擦角的预测值为0.905，仿真与理论误差2.2%，表明仿真结果与试验结果一致，则可确定仿真参数 µ1=0.885。

2.3 EPS 颗粒之间滚动摩擦系数测定

离散元的出现源于分子动力学，其将整个介质看作是一系列离散的独立运动的单元组成，单元本身就具有一定的几何形状、物理、化学性质。基于分子动力学仿真模拟出EPS 颗粒单元的滚动摩擦系数f1，模拟过程如图7 所示，两个相同的聚苯乙烯球形颗粒单元作为对象，对颗粒进行点接触滚动运动模拟。聚苯乙烯是一种只含有碳氢元素的聚合物(C8H8)，使用Material Studio 软件建立颗粒运动模型，构建两个材料相同，半径20 nm，密度均为20 kg/ m3的球形单元。在分子动力学模拟中，将10个聚苯乙烯分子首尾相连组成分子链，球形单元由聚苯乙烯分子链填充，分子链填充量使球形单元密度达20 kg/ m3为 止。对颗粒1 施加载荷Fz=10 nN，方向为z轴负方向，赋予颗粒1 沿V方向速度为0.1 m/s 的运动，模拟运动过程中小球1 和小球2 在点接触时发生滚动运动。

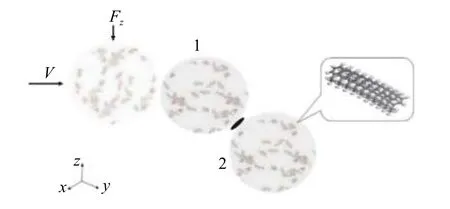
图7 颗粒单元滚动碰撞工况

本实验中的滚动摩擦系数K计算公式为

式中：T——颗粒单元接触时的切向力；

N——接触时候的法向力；

R——颗粒1 的半径。

模拟温度通过Nose-Hoover 热浴法设定在300 K，耦合时间为0.1 ps，压强保持为1 atm，分子动力学模拟通过Lammps 软件完成。输出仿真过程中颗粒之间的滚动摩擦系数值f1，除去突变的数值，剩余滚动摩擦系数一直维持在0.02，则在接下来的离散元仿真模拟时f1为0.02。

2.4 堆积实验分析和测定参数

前文已经对 µ1、ε1、f1完成测定。下文对EPS 颗粒与PVC 滚动摩擦因数f2，EPS 颗粒之间碰撞恢复系数 ε2、静摩擦因数 µ2进行分析和测定。为避免物理测定带来的较大误差，通过颗粒堆积实验与仿真相结合，以休止角为响应，根据最陡爬坡实验确定参数 µ2、ε2、f2最佳范围，结合Box-Behnken 实验建立休止角与参数的二阶回归模型，对参数进行求解。

2.4.1 堆积实验休止角测量

堆积实验如图8(a)所示，材料选择EPS 颗粒，底板选用PVC 软膜，圆柱管为内径41 mm，长度为190 mm 玻璃管。通过电机伸缩杆末端固定玻璃管并匀速提升，EPS 颗粒自然滑落并堆积如图8（b）。

图8 颗粒堆积实验

堆积实验采集到的图像如图9(a)所示，为保证测量休止角的精准性，使用Matlab 读取实验图像，依次对图像进行去噪处理，灰度处理，二值化处理，最后提取轮廓边界点，利用最小二乘法对边界点进行直线拟合，拟合的直线斜率即为所要测得的休止角正切值。利用同种测量方法实验五次，求斜率均值为0.25594，则EPS 颗粒在PVC 软膜上的休止角θ为14.356°。

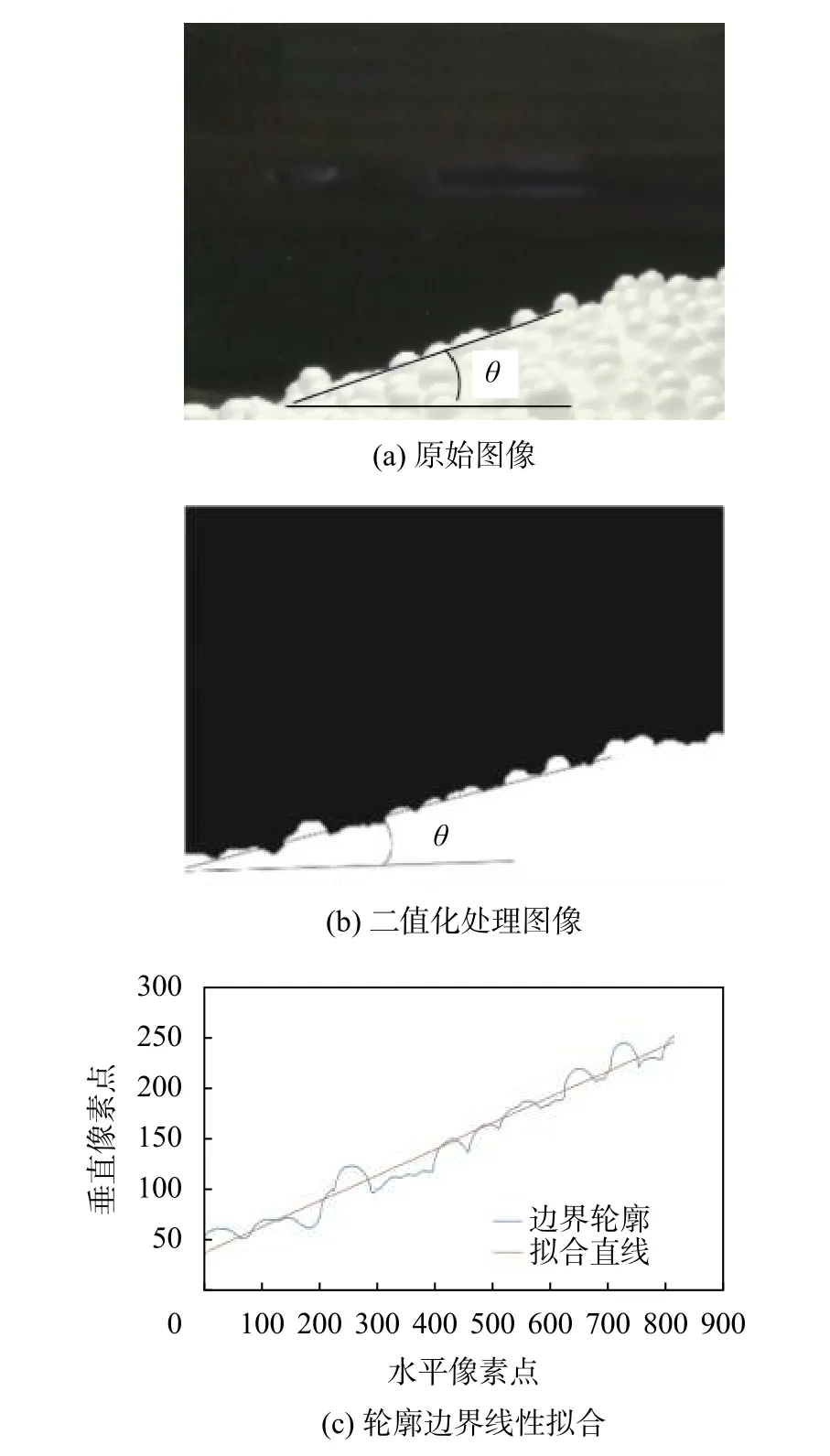
图9 休止角测量

2.4.2 最陡爬坡实验

使用离散元仿真软件EDEM 进行如图10 颗粒堆积仿真实验，通过改变 ε2、f2、µ2三个参数，对仿真实验的休止角θ 进行测定，颗粒的其余参数均采用已测定数值。

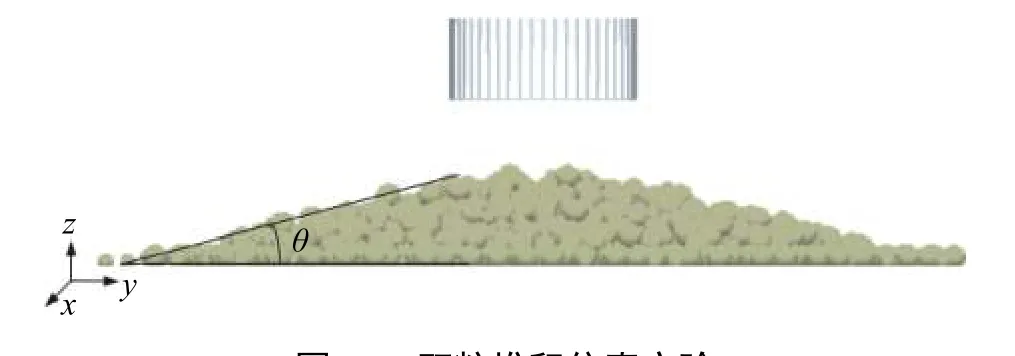
图10 颗粒堆积仿真实验

在一定范围内f2、µ2增大会使休止角增加[15]，ε2的增大会导致休止角减小，结合细观参数对休止角的影响研究结论[16]，确定爬坡试验的方向和步长。通过前期的预仿真，ε2、f2、µ2的参数选择区间以及实验结果如表3 所示。可知仿真休止角与试验测量休止角最小误差在第c、d、e 组区域，由d 组实验可以看出当 µ2为 0 .4，f2为 0.44，ε2为0.35 时，仿真休止角值与实验值比较接近。

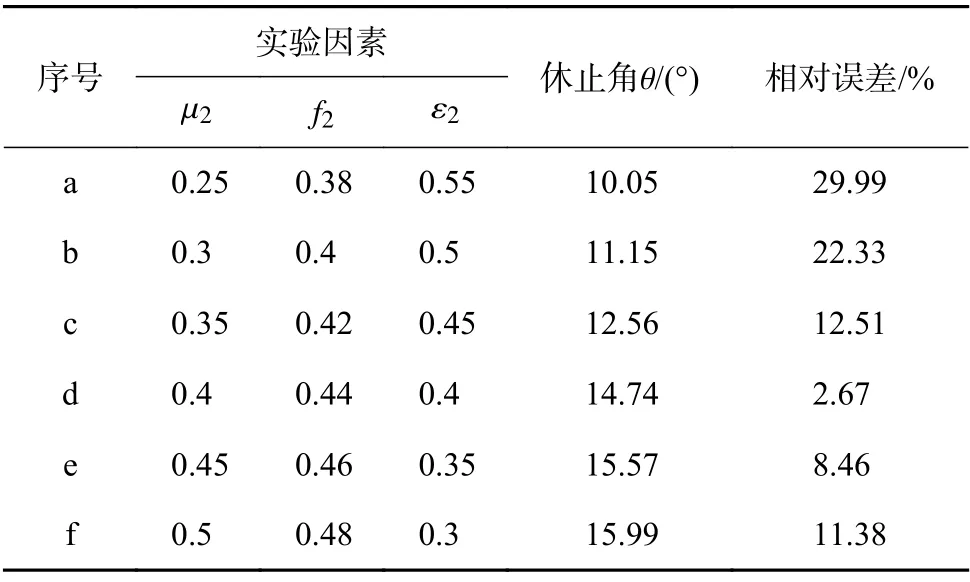
表3 最陡爬坡实验设计及其结果

2.4.3 响应面分析

结合最陡爬坡实验选定d 组参数为中心点，确定三个参数合理范围，根据Box-Behnken 中心组合设计原理[17]，以–1,0,1 为低、中、高水平进行三因素三水平的响应面实验，响应值为休止角θ，如表4 所示。

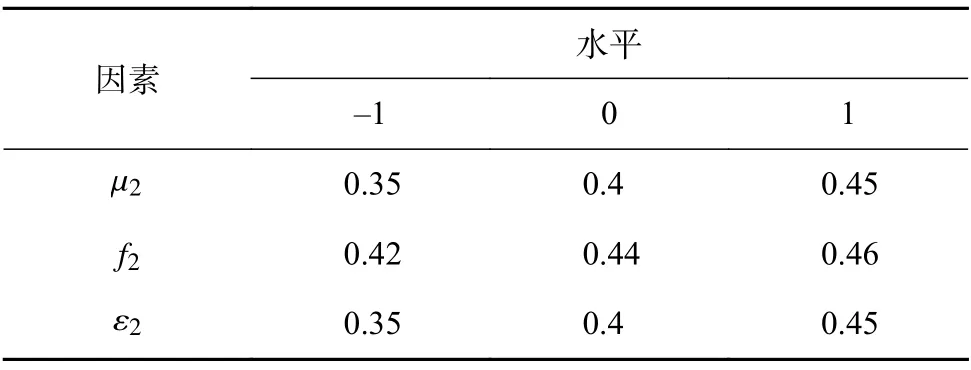
表4 仿真实验因素与水平

响应面实验设计及结果如表5 所示，用软件Design-expert 对实验结果进行回归分析得到回归方程为：

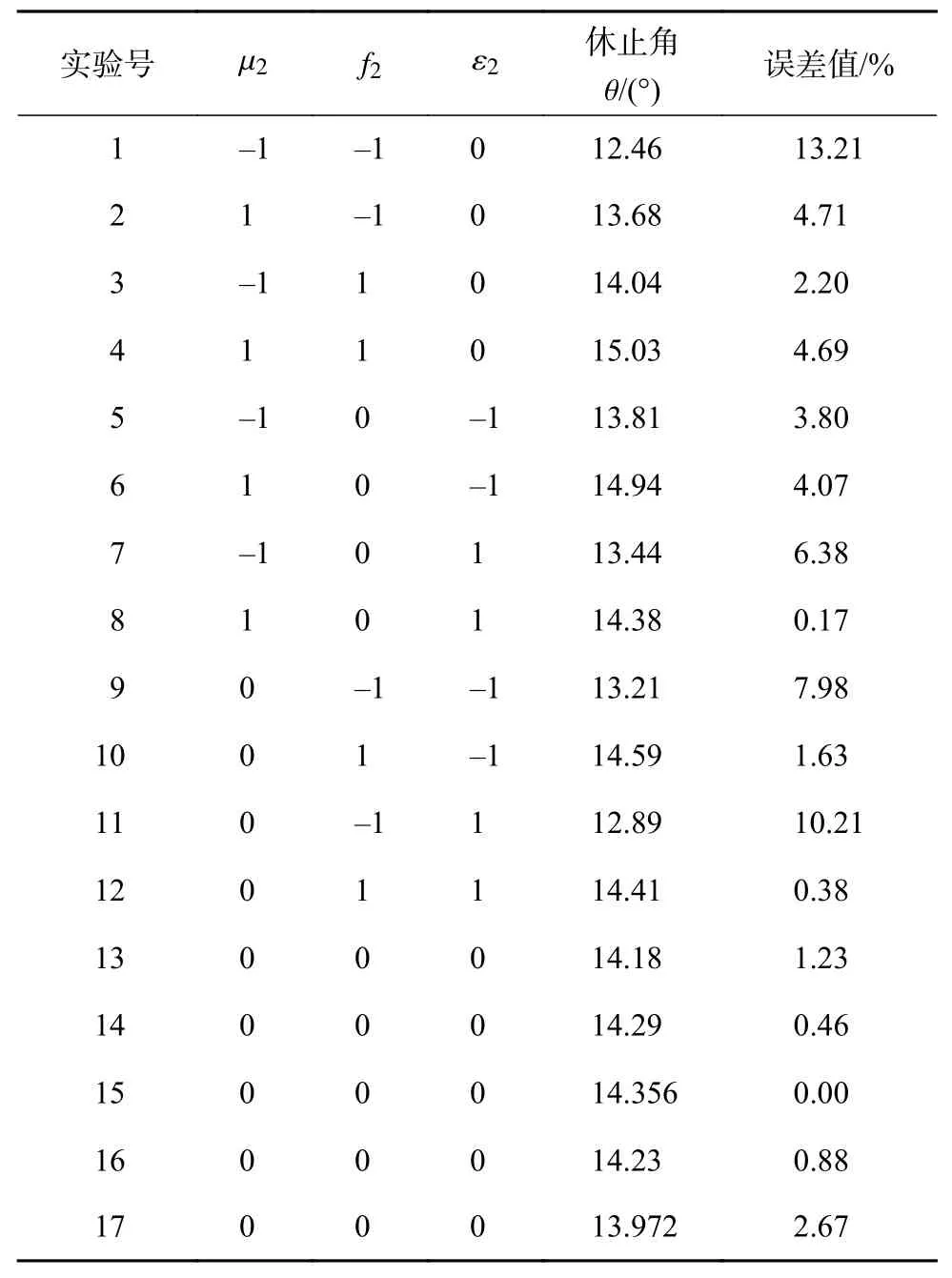
表5 Box-Behnken 实验设计及结果

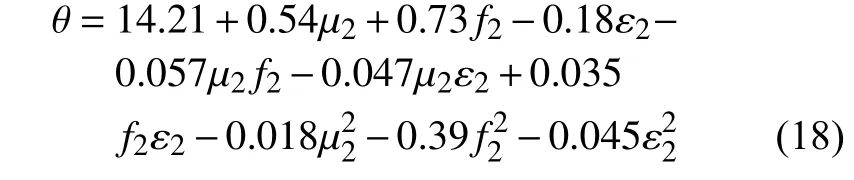
对休止角的模型进行方差分析如表6 所示，方程模型极显著（P<0.0001），失拟项不显著（P=0.7612>0.05），模型稳定。相关系数r2值为0.9853，校正决定系数=0.9665，预测决定系数=0.9282，三者都大于0.8，信噪比为26.142>4 表明模型精确度很高。

表6 实验模型方差分析

根据表7 结果可知，在保证模型的准确性前提下，剔除对休止角影响不显著的项（P>0.05），优化后得到新的模型为

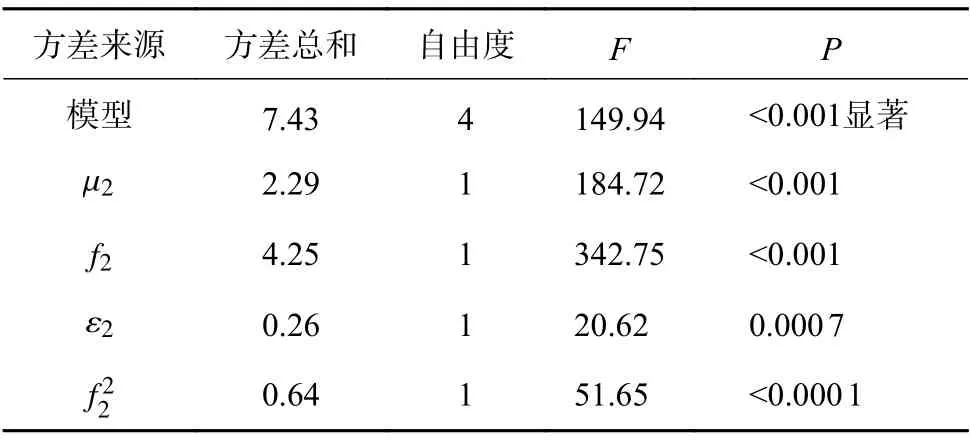
表7 优化模型方差分析

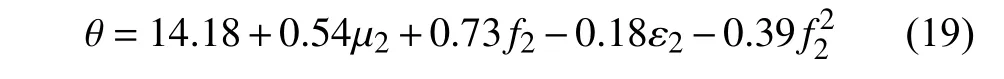
r2=0.9804，，信噪比41.86，模型较之前精确度更高。

2.4.4 最优参数的选取

利用Design-Expert 三维响应表面，设置优化目标为休止角接近14.356°，误差值优化目标为最小，对模型进行求解，选取最优参数值,颗粒与颗粒静摩擦因数 µ2，颗粒与PVC 滚动摩擦f2，颗粒与颗粒之间恢复系数 ε2的约束函数是：

得到最优的参数组合为：颗粒与颗粒之间静止摩擦因数 µ2=0.40，恢复系数 ε2=0.43，颗粒与PVC软膜之间的滚动摩擦因数f2=0.45。用最佳的参数组合进行三次休止角仿真实验，得到的仿真休止角度数均值14.352°。由于堆积试验休止角的角度为14.356°，仿真与实测的休止角误差为0.124%，表明测定的参数组合与试验参数相符。

3 试验验证

为验证前文测定的颗粒与颗粒之间静止摩擦因数、滚动摩擦因数、碰撞恢复系数，颗粒与PVC 软膜之间的静止摩擦因数、滚动摩擦因数、碰撞恢复系数的准确性，将六个参数值：0.40、0.02、0.43、0.885、0.45、0.506 代入EDEM 仿真软件，进行侧壁坍塌仿真实验[18]。

如图11(a)所示，实验器材由箱体（长90 mm,宽90 mm，高90 mm）和玻璃挡板组成，为控制实验对象的接触参数数量，箱体墙壁以PVC 软膜覆盖。实验时以较慢速度向上抬升玻璃挡板，使EPS 颗粒在PVC 软膜上充分扩散，当颗粒散体稳定之后进行水平拍照，将采集到的图片进行2.4 节相同步骤图像处理，重复实验5 次并测量休止角，取均值为18.08°。将上述测定的参数带入侧壁坍塌仿真实验如图11(b)，测量仿真实验的坍塌休止角，实验进行5 次。测量休止角均值为18.43°，与试验所测量的休止角相对误差为1.9%，表明仿真实验中的结果和实际情况吻合，参数验证合理。由此可得上述参数f1、µ1、ε1、f2、µ2、ε2适用于EPS 颗粒和PVC 软膜的离散元分析，在类似的弹性颗粒和柔性体的接触该测定方法同样适用。

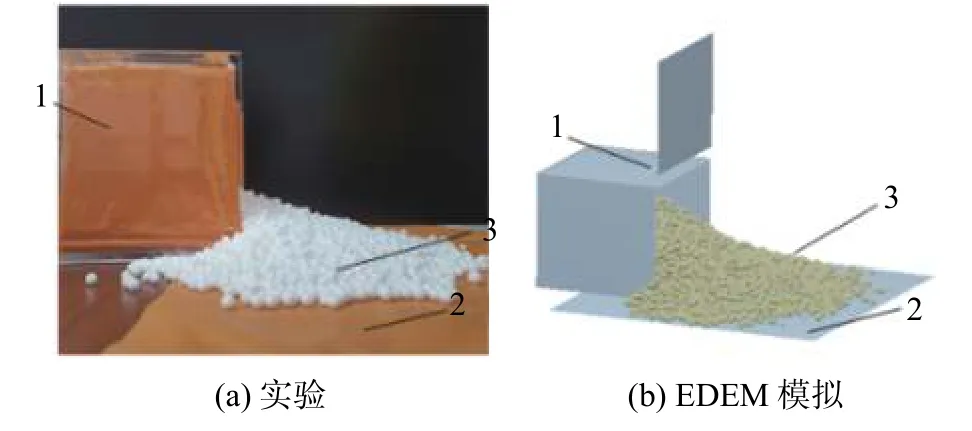
图11 侧壁崩塌实验

4 结束语

1）以EPS 颗粒和PVC 软膜为研究对象，基于Hertz-Mindlin 接触模型，利用实验和仿真进行颗粒与软膜之间的参数测定，得出EPS 颗粒与PVC 软膜的静摩擦因数为0.885，恢复系数为0.506。通过分子动力学的仿真模拟方法，标定出颗粒与颗粒之间的滚动摩擦因数为0.02。

2）对颗粒与颗粒的碰撞恢复系数，颗粒与PVC软膜的滚动摩擦系数，颗粒与颗粒的静止摩擦系数进行参数测定：通过设计最陡爬坡法逼近最大响应区域，结合Box-Behnken 响应面实验，以颗粒堆积实验休止角为响应值，选取与实验测量休止角误差值最小的参数组合为最优解，得三者参数分别为0.43、0.45、0.40。

3）通过侧壁崩塌实验验证参数的可靠性，发现崩塌实验的仿真值和实验值休止角结果接近，误差为1.9%，说明接触参数的测定准确，也为研究柔性体和颗粒细观接触参数提供了具体的测定方法。