多源信息融合的水轮机组振动测量方法
2021-10-23谭丕成朱红平曾辉斌
谭丕成,万 元,朱红平,胡 边,曾辉斌,刘 宇
(1.五凌电力有限公司近尾洲水电厂,湖南 衡阳 421127;2.湖南五凌电力科技有限公司,湖南 长沙 410004;3.国家电投集团水电产业创新中心,湖南 长沙 410004)
0 引 言
我国拥有世界第一的水电资源蕴藏量,有着巨大的开发潜力。随着新能源产业的不断发展,水力资源作为清洁能源的重要组成部分越来越受到重视。水电机组作为水力发电的核心装备,其运行状态关系到发电效率、经济效益以及生产安全。
作为回转机械,在运行过程中因由异常振动引发的水轮机组故障而影响电力生产的现象很普遍[1]。当水轮机组振动幅度超过允许值或者振动频率出现异常时,轻则引发调速器的振荡,降低发电效率,重则会损坏机组的重要部件(如尾水管里衬脱落,螺栓剪断,转轮叶片裂纹甚至断裂等,浙江富春江水电站曾发生过机组的异常振动故障),增加检修次数和检修工期,降低使用寿命;更为严重的会引起水工建筑物的振动,危及水电站安全[2-4]。因此,为了维持水电机组的安全运行,保障水电厂安全生产,对机组运行过程中的振动信号进行准确的测量与实时的监视具有重要意义。
目前,用于在线测量与检测的手段很多,其中以振动信号为基础的测量与分析方法,具有信号采集简便,物理意义明确,特征识别简单等特点成为检测与诊断中最常用、最有效的手段[5-6]。但在一些较为复杂的工况下,一方面由于振动传感器的布设受限于设备或作业环境,不易找到可靠的安装点位;另一方面,由于安装位置无法选择在接近振动源的区域,例如水轮机组外部壳体,其表面振动信号较弱,并不容易采集,使得振动诊断法有一定的局限性。声学故障诊断技术是基于声音信号的检测分析方法,声学传感器的具有体积小、易安装的特点,在早期的机械齿轮故障诊断中已有一定的应用[7-9]。但是在缺少先验的故障信息或者声学特征的前提下,传统的声学诊断(acoustic-based diagnosis,ABD)方法在实际操作中不易找到准确的测量位置;基于单一传感器信息的 ABD 方法更容易受到测量位置的影响,无法充分利用声音信息,在局部诊断存在局限性[10-12]。而且水轮机组工作时干扰噪声复杂,对于测量精度有较大影响。
为了克服振动信号测量方法与声音信号测量方法的不足,本文提出了一种多源信息融合的水轮机组振动检测方法。通过多源信息融合算法,实现振动信号与声音信号的融合,通过多源信息融合与能量重心法的结合[13],实现水轮机组振动频率的准确分析。
1 基于多源信息融合的测量方法
水轮机组的结构复杂、振动激励源多,工况复杂,同时单一传感器采集到的信息都会受到周围环境的干扰,获取的信息是不精确的。多源信息融合的优点在于能够最大效率的利用多个维度的信息对信号特征进行描述,对于不确定性的干扰有较好的屏蔽作用,可以实现目标信息的准确提取,有效提高信息特征提取的的效率,提高对干扰和噪声的抵抗能力。多源信息融合的功能可以概括为:扩大信号的探测范围,提高特征提取性能,改进抗干扰能力;提高对目标信号的时频分辨能力,从多个维度提取目标的特征矢量,改善特征提取的准确性,降低噪声干扰;使得系统的容错能力和自适应能力得到进一步提高;进而使得下一步的决策有更多维度的数据基础,提高系统决策能力,从而使整个系统的性能提升。得益于多源信息的冗余性和互补性,通过多源信息融合得到的结果与单一传感器获得的信息相比,其抗干扰能力和准确性往往会有质的飞跃。
在水轮机组的实际测量过程中,声音与振动往往是密切相关的,因此,一般情况下振动频率与音频信号具有很强的相关性[14],为实现振动信号与音频信号的多源信息融合,本文所提出的方法通过对多个检测点的声音信号与振动信号进行同步采集,采用多源信息融合算法,通过强化振动信号与音频信号的同频成分,抑制干扰信号与噪声,对信号进行重构,得到融合信号,实现对目标信息的准确提取。基于多源信息融合的测量方法如图1 所示。
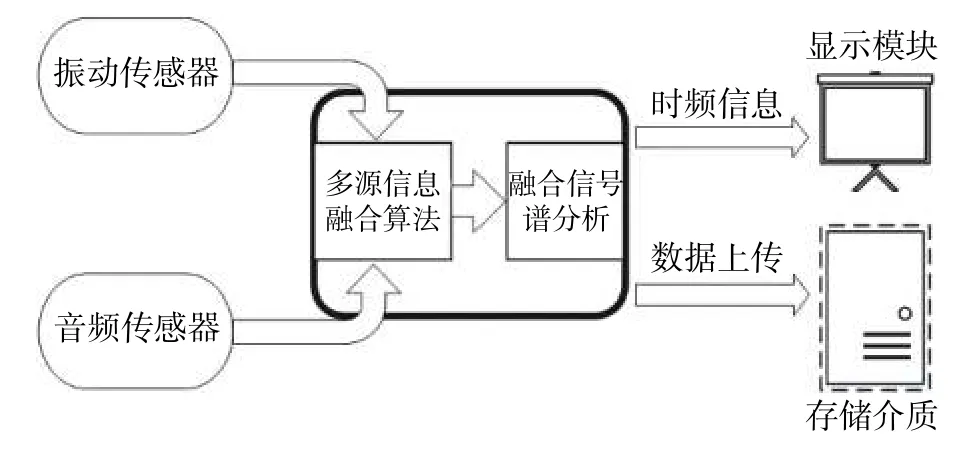
图1 测量系统结构图
通过对重构的的融合信号进行谱分析,可以在时频域内得到更精准的结果,同时可通过实时存储便于信息的回溯与比较。
2 多源信息融合的信号重构
在水轮机组的振动与声音信号中,除了反映振动频率的基频成分,还会存在由于其他机械结构振动带来的干扰成分。为了抑制干扰,增强基频信号,本文提出了一种基于多源信息融合的信号重构方法,将振动与音频信号进行融合重构,从而实现对干扰与噪声的抑制。
一般情况下,在振动信号和声音信号传播的过程中,两种信号中引入的干扰成分通常是不同的,也就是说,振动信号和音频信号有着相同的基频和不同的干扰频率。假设v(t)表示振动信号,a(t)表示音频信号,振动信号和音频信号的模型可表示为如下所示:

式中:A0——基频幅值,V;
f0——基频频率,Hz;
φ0——基频相位,rad;
Avi——振动干扰幅值,V;
Aai——音频干扰幅值,V;
fvi——振动干扰频率,Hz;
fai——音频干扰频率,Hz;
φi——干扰信号相位,rad;
na(t)和nv(t)——振动信号和音频信号中的高斯白噪声。
在振动信号和音频信号中,代表振动频率的基频信号与干扰信号和白噪声是线性叠加的,因此振动音频互相关序列可以根据互相关运算的性质表达为各个信号成分互相关的叠加。为了表达的简洁,本文将互相关序列分成三个部分。第一部分是振动信号和音频信号中同频成分的互相关,第二部分是振动信号和音频信号中不同频率成分的互相关,第三部分是高斯白噪声和各个频率成分的互相关,各个部分的表达式如下所示:
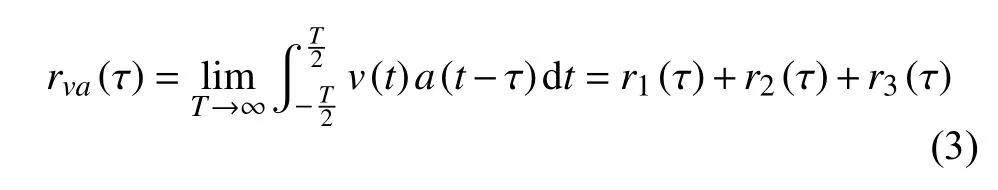
其中rva表示振动信号与音频信号的互相关,r1表示振动信号和音频信号中同频成分的互相关,r2表示振动信号和音频信号中不同频率成分的互相关,r3表示高斯白噪声和各个频率成分的互相关。

振动音频互相关序列的频域特性可通过傅里叶变换求得,根据互相关与傅里叶的性质,互相关序列的频谱可表示为(式中*表示共轭):

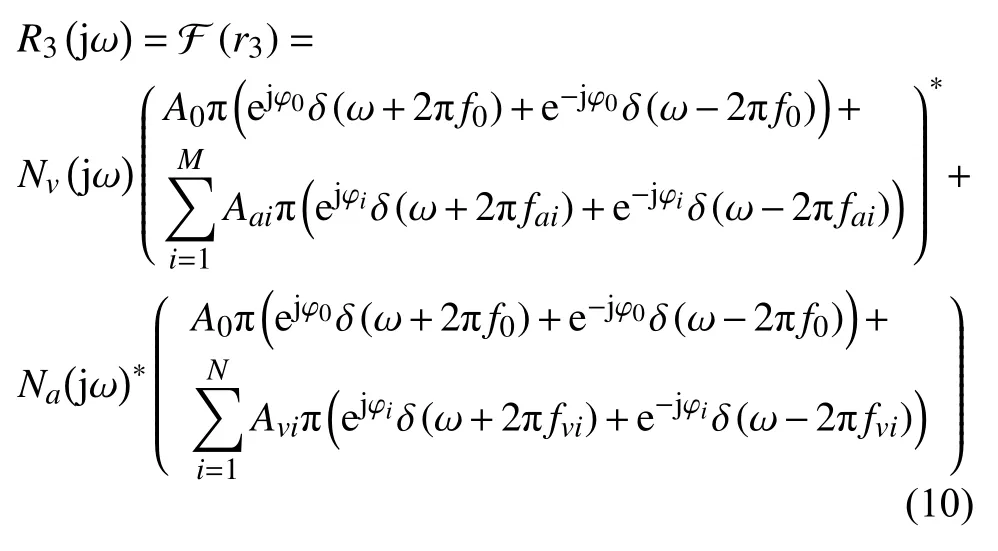
基于互相关的性质,同频成分经过互相关后获得增强,不同频率成分和噪声由于没有相关性,经过互相关运算后相互抑制[15],因此R1>>R2+R3,所以互相关序列的频谱成分可以简化为:
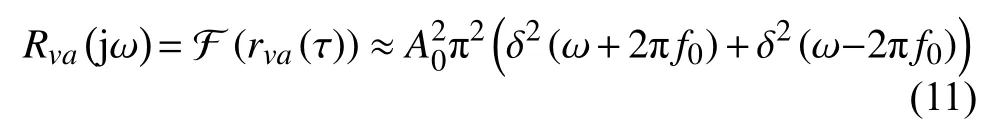
由此可知,经过融合重构之后,振动信号和音频信号中代表水轮机组振动频率的基频信号得到增强,干扰信号和噪声被抑制。在振动传感器与音频传感器布设在同一区域时,振动信号和音频信号均包含反映振动频率的基频信号,因此基于融合重构序列能够更好地提取水轮机组振动频率信息。
3 基于能量重心法的频率校正方法
为实现对基频的精确估计,本文采用能量重心法对基频频率进行精确估计。能量重心法算法具有操作简单,运算量小的优点,通常只需较少的采样点数,可根据需求选择不同的窗函数的校正公式。然而实际中采集到的信号往往伴随有噪声干扰,噪声会影响谱线的正确选择,进而会影响到频率的估计精度。在本文中,通过对多路信号进行多源信息融合,重构后得到的融合信号抑制了大部分噪声与干扰,使得谱线的选择更加准确。
一般情况下,窗函数离散频谱的能量重心具有无穷逼近坐标原点的性质,能量重心法的提出就是基于窗函数的这一特性。对于频率、幅值和相位分别为f0、A0、θ0的单一谐波信号x(t)=A0cos(2πf0t+θ0),它的傅里叶变换可表示为:

其中w(n)为窗函数。将频率f0归一化,并表示为f01,此时幅值谱的谱峰位于谱线k0=int(f01),则归一化频率f01与谱线k0存在如下关系:f01=k0+δ,其中δ 为归一化频率校正量,且–0.5<δ≤0.5。
令G(i)为加窗信号功率谱第i条谱线值,k0对应主瓣内峰值谱线,则根据重心特性,当n→∞有

由上式可以求得主瓣中心,即归一化校正频率
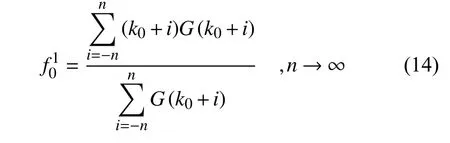
频率修正的算法流程如图2 所示。
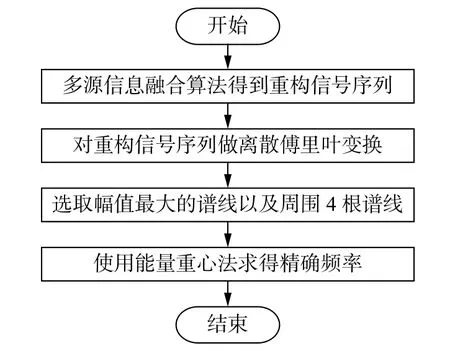
图2 算法流程图
首先,确定窗长,将采集的振动信号和音频信号通过多源信息融合方法进行重构,得到融合信号序列,然后对融合信号序列做离散傅里叶变换,得到融合信号序列的频谱参数。由于干扰频率成分和噪声被抑制,基频成分得到增强,幅值最大的谱线就代表基频成分的频率。选出幅值最大的谱线及其周围的4 根额外谱线,通过能量重心法求得精确频率。
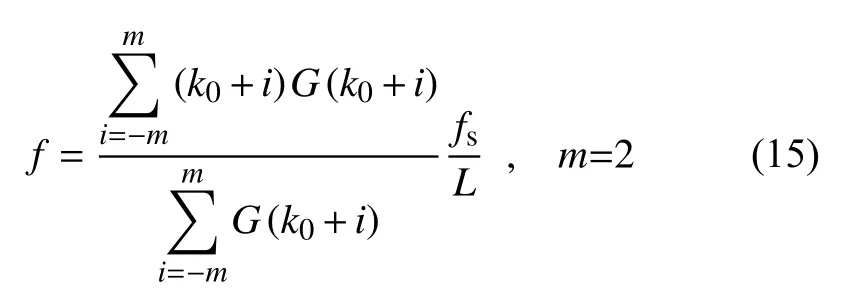
式中:k0——幅值最大谱线的序号;
G(k0+i)——序号为k0+i的谱线的幅值;
fs——采样频率;
L——参与离散傅里叶变换的点数;
f——修正后的频率。
4 仿真与实测信号分析
为验证多源信息融合算法在抑制噪声与提高精度方面的效果,本文采取了仿真模拟测试的形式,将多源信息融合方法与传统单传感器测量方法进行比较。模拟测试采取信号源加模态激振器的形式模拟机械振动工况,仿真试验台如图3 所示。信号源设置为55 Hz 正弦信号,采样率设置为5 kHz,在信噪比分别为20 dB,40 dB 和60 dB 的条件下进行测试,频率估计误差结果如表1 所示,从仿真结果可以看出,在噪声较强的情况下,单一传感器的测量结果误差较大,而经过多源信息融合后,由于噪声干扰被抑制,频率估计结果得到较为显著的改善,误差降低了一个数量级。

图3 振动仿真试验台
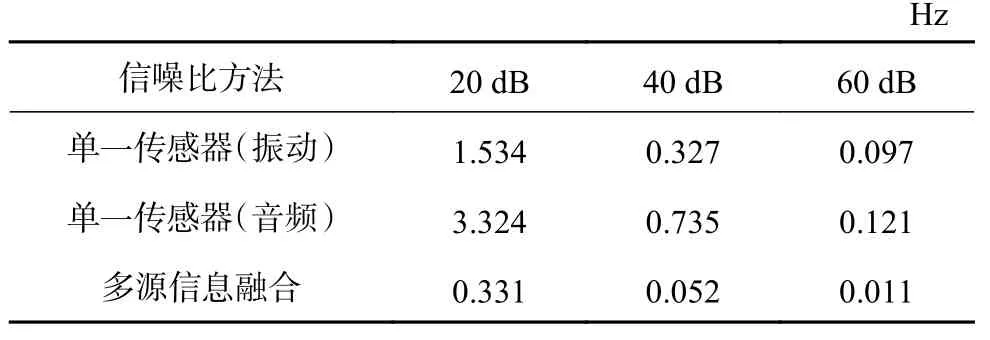
表1 不同信噪比的频率估计绝对误差
为验证算法在实际应用中的表现与可靠性,实测实验场地选择在五凌电力近尾洲水电厂的1 号水轮机组。机组为灯泡式贯流发电机组。通过对灯泡头进行振动与音频信号的采集,并通过对贯流式水轮机组的振动与音频数据进行分析,测量准确的机组振动频率。
实测数据分析分为两个部分,第一部分是在稳定负荷情况下的测量,第二部分实在变负荷情况下的测量。由于机组的振动频率主要是以低频为主,因此采样率fs设置为2 kHz,并通过低通滤波电路滤除部分高频噪声。
首先,在负荷稳定情况下,灯泡头的振动时频分析图如图4、图5、图6 所示。
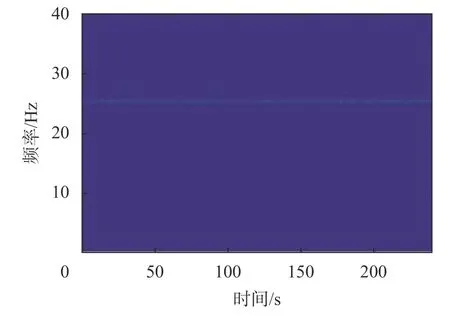
图4 稳定负荷振动信号时频图
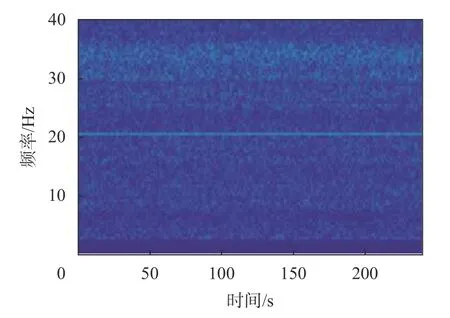
图5 稳定负荷音频信号时频图
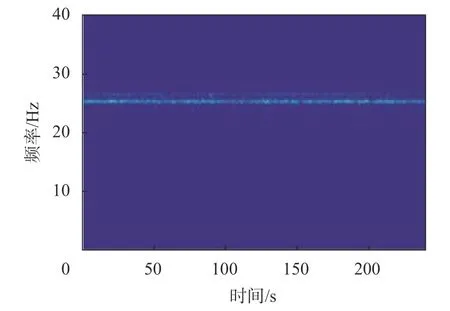
图6 稳定负荷融合信号时频图
从时频图中可以看出,采用多源信息融合算法得到的时频图能量更集中,干扰成分被显著抑制,而振动和音频信号都存在主频能量较弱,干扰成分较多的问题。机组振动频率估计结果如图7 及图8所示,表2 为图8 所示时间段内的频率测量结果。从频率估计的结果来看,基于多源信息融合的方法能够更准确的对机组振动频率进行估计,在稳态情况下能够准确地估计出机组的振动频率,并且有较好的抗干扰能力,而单纯依靠振动或者音频信号的方法则跟容易受到干扰信号的影响,在测量过程中容易产生异常波动,尤其是音频信号的估计结果,由于现场工况复杂,干扰信号较强,估计结果产生显著偏差。
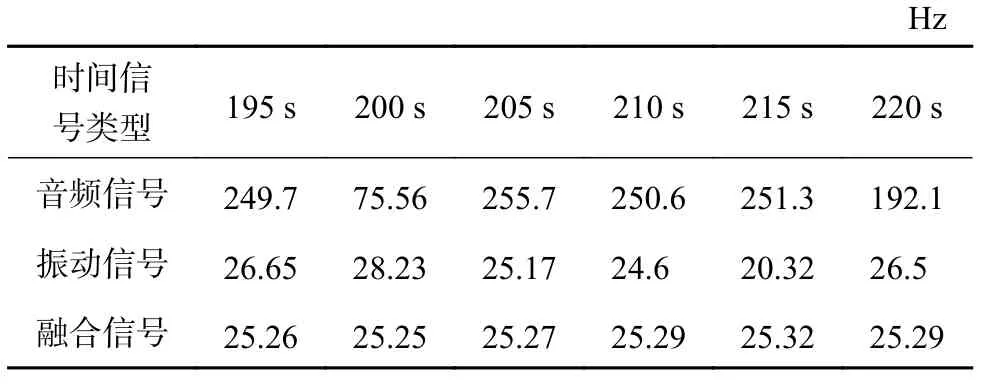
表2 A 区域频率估计结果
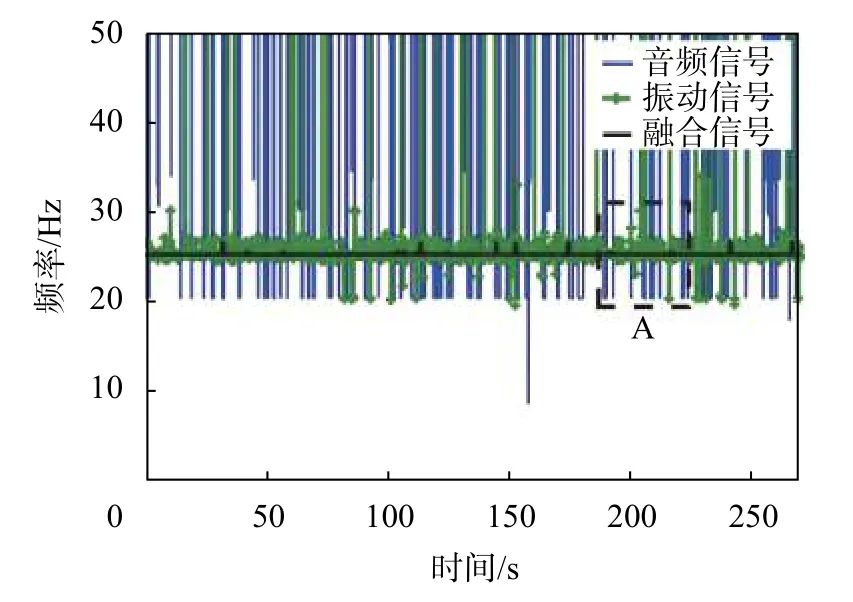
图7 稳态情况下频率估计结果对比

图8 A 区域放大图
在变负荷的情况下,负荷在约67 s 时发生变化,机组振动时频分析图如图9、图10、图11 所示。
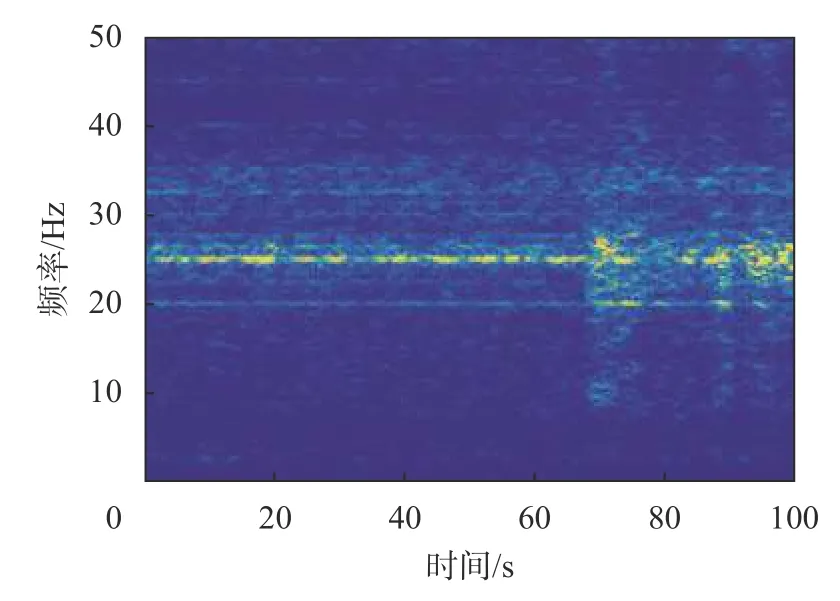
图9 变负荷振动信号时频图

图10 变负荷音频信号时频图
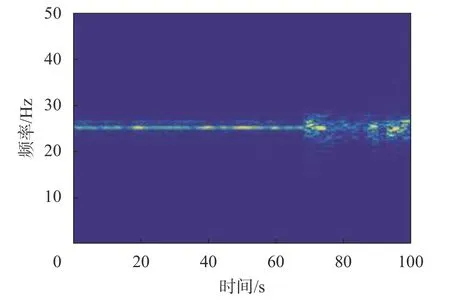
图11 变负荷融合信号时频图
从时频图中可以看出,采用多源信息融合算法得到的时频图能量更集中,干扰成分被显著抑制,在变负荷的阶段,主频的波动更为明显,而振动和音频信号都存在主频能量较弱,干扰成分较多的问题,在变负荷的阶段主频变得模糊并且难以分辨。机组振动频率估计结果如图12 与图13 所示,从频率估计的结果来看,基于多源信息融合的方法能够更准确的对机组振动频率进行估计,并且有较好的抗干扰能力,并且在变负荷阶段能够跟踪振动频率的变化。而单纯依靠振动或者音频信号的方法则跟容易受到干扰信号的影响从而导致结果出现显著的偏差,尤其是在变负荷阶段,由于该阶段的干扰相较于平稳负荷情况下更加复杂,从图13 可以看出,振动信号与音频信号的估计结果波动范围很大,而实际情况下,机组的振动频率不可能发生如此剧烈的变化,因此显然是由干扰信号导致的估计偏差,无法准确捕捉频率的变化。
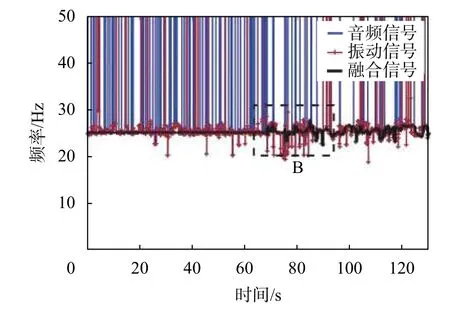
图12 动态情况下频率估计结果对比

图13 B 区域放大图
5 结束语
本文提出了一种基于融合声音与振动信号的水轮机组振动检测方法。通过多源信息融合算法,对振动信号与声音信号进行融合重构,利用振动与声音的相关特性,抑制了干扰信号和背景噪声的影响,增强了基频的能量,通过能量重心法对融合信号进行频率校正,实现水轮机组振动频率的准确估计。通过模拟仿真实验验证了多源融合方法对噪声与干扰的抑制效果。通过对五凌电力近尾洲水电厂的1号水轮机组的实测实验,验证了本文所提出方法的可靠性,通过与单纯的振动信号分析方法和音频信号分析方法比较可知,本文所提出的多源信息融合算法能有效抑制干扰信号和背景噪声,提高了振动频率测量的准确性和可靠性。
