Energy-Efficient Optimal Guaranteed Cost Intermittent-Switch Control of a Direct Expansion Air Conditioning System
2021-10-23JunMeiZhenyuLuJunhaoHuandYulingFan
Jun Mei,Zhenyu Lu,Junhao Hu,and Yuling Fan
Abstract—To improve the energy efficiency of a direct expansion air conditioning (DX A/C)system while guaranteeing occupancy comfort,a hierarchical controller for a DX A/C system with uncertain parameters is proposed.The control strategy consists of an open loop optimization controller and a closed-loop guaranteed cost periodically intermittent-switch controller(GCPISC).The error dynamics system of the closed-loop control is modelled based on the GCPISC principle.The difference,compared to the previous DX A/C system control methods,is that the controller designed in this paper performs control at discrete times.For the ease of designing the controller,a series of matrix inequalities are derived to be the sufficient conditions of the lower-layer closed-loop GCPISC controller.In this way,the DX A/C system output is derived to follow the optimal references obtained through the upper-layer open loop controller in exponential time,and the energy efficiency of the system is improved.Moreover,a static optimization problem is addressed for obtaining an optimal GCPISC law to ensure a minimum upper bound on the DX A/C system performance considering energy efficiency and output tracking error.The advantages of the designed hierarchical controller for a DX A/C system with uncertain parameters are demonstrated through some simulation results.
I.INTRODUCTION
THE building sector consumes about 30%−40% of the whole energy in the world [1].Among energy consumption of a general building,the heating,ventilation,and air conditioning (HVAC)system bears the greatest energy demand as it consumes approximately 50% of the building’s total energy usage.Therefore,improving the energy performance of the HVAC systems allows for decreasing energy demands of buildings.Although there are many methods to improve the energy efficiency of buildings,such as hybrid energy supplies [2],[3],facility retrofit and maintenance [4],[5],envelope retrofit [6],etc.,energyefficient optimal control of HVAC systems has greater potential in the reduction of energy consumption and cost of buildings in comparison.Due to this,effective control of HVAC systems has drawn much attention.
To control HVAC systems,advanced control approaches have been developed [7]–[10] to improve indoor thermal comfort efficiently.A gain scheduled control approach was proposed [7] to improve the energy and comfort performances of an HVAC system as well as to satisfy the changing demands for cooling capacity.In [9],a real-time eventtriggered adaptive critic controller was designed for nearoptimal temperature control of a multi-zone HVAC system.With an event-based controller [11],the multi-zone HVAC control problem was formulated to maintain indoor thermal comfort in an energy-efficient manner.In recent years,modelbased predictive control (MPC)as an advantaged control scheme is widely employed in building HVAC systems to control energy efficiency and occupancy comfort [12]–[14].
Compared to conventional HVAC systems,direct expansion air conditioning (DX A/C)systems have the advantages of energy efficiency,lower costs,and simpler system configurations [15].That is why DX A/C systems are widely investigated and adopted in the building sector,and particularly used in small/medium sized buildings over recent decades.In [16],a linear-quadratic-Gaussian (LQG)controller was investigated for simultaneous control of indoor moisture content and air temperature.An open loop controller and an MPC controller were proposed for improving the energy and comfort performances of a building’s DX A/C system [17],[18].In this way,an optimal occupancy comfort can be ensured and simultaneously the energy demand of target buildings can be reduced optimally.
In the previous work,various control strategies were employed for better energy performance of building DX A/C systems.In this research,the DX evaporator’s dry-cooling and wet-cooling areas were assumed to be constant.However,the stability of the dry-cooling and wet-cooling areas in the DX evaporator are not clear and may change over time and under different circumstances [19].It requires high accuracy in the control and operation of the DX A/C system,especially when the system tracking time-varying references.However,previous control methods (i.e.,LQG and MPC)are difficult to control the systems using time-varying dry-cooling and wetcooling areas and uncertain parameters.To facilitate the closed-loop control design,the first-order approximation of the Taylor based linearization is employed to linearize the nonlinear models in [16]–[18],[20].However,the local linearization method inevitably results in less accurate control.Guaranteed cost control (GCC)is capable of handling the stability of the various dynamic systems with time-varying and uncertain parameters and ensuring adequate performance of the control system [21].GCC has attracted widespread attention in recent years [22]–[24].It is meant to address a guaranteed cost controller for a time-varying DX A/C system with uncertain parameters for improving the occupancy comfort and energy performances of a target building.
Once the speeds of the supply fan and the compressor of the DX A/C system reach the values,and the relative humidity and indoor air temperature are within the suitable ranges or deadband,maintaining the target speeds is relatively easy.This is because of the higher cooling capacity indoors and the closed operational status of the electronic expansion valve(EEV),which leads to turning off the indoor air unit to avoid energy waste [10].We notice that this working mechanism is similar to an intermittent control way.In recent years,intermittent control has been widely investigated [25]–[27]and has potential application value in engineering fields [28].The reasons are that the method is not only economical,but is also capable of decreasing the amount of information transmitted.In the method,the working time is divided into nonzero control intervals,in which the intermittent control is on,and others in which the intermittent feedback control is off.Also,the intermittent controller is more efficient compared to continuous controllers,because the system’s input using intermittent control is measured intermittently instead of being measured continuously.In light of these advantages,intermittent controllers are used for controlling various control systems [26],[29],[30].However,the intermittent control methods in the literature do not consider the performance of dynamic control systems.For instance,the HVAC systems are expected to guarantee the thermal comfort of target buildings with a high level of energy efficiency.The compressor should avoid frequently starting and stopping in order to reduce compressor loss and improve energy utilization rates to avoid energy loss.For energy savings,a switch control method is needed to control the compressor.Therefore,it is meaningful to investigate guaranteed cost intermittent and continuous feedback control problems in dynamic control systems.
In this context,guaranteed cost intermittent and switch regulation control problems for a DX A/C system,which exhibits uncertain parameters,state constraints,and control constraints,are proposed and studied.Nonlinear control systems are designed for guaranteeing good indoor thermal comfort.During the design process,the coupling effects between the two objects are taken into consideration.Based on the energy consumption of the DX A/C system,an energyoptimised open loop controller is designed to achieve maximum energy efficiency.The resulting steady state solution is then followed by an intermittent control strategy,which is designed with a guaranteed cost to adjust the relative humidity and air temperature to the steady state while maximizing the energy efficiency.According to the guaranteed cost intermittent-switch regulation control strategy and Lyapunov stability theory,a series of sufficient conditions for the proposed guaranteed cost periodically intermittentswitch controller (GCPISC)are provided based on matrix inequalities,which ensures the DX A/C system with uncertain parameters maintained at the optimal steady state with good control performances on energy efficiency and thermal comfort.Moreover,an open loop issue is optimized to get the optimal GCPISC law,which ensures the minimization of the guarantee cost function’s upper bound with the given sufficient conditions,uncertain parameters and states,and input constraints.The simulation results show that the energy consumption of the DX A/C system is reduced and good occupancy comfort is maintained,which demonstrates the validity of the hierarchical control method presented in this paper.
The main contributions of this research are below.Firstly,a guaranteed cost intermittent-switch control problem is investigated.Secondly,the GCPISC is used in a building’s DX A/C system.Thirdly,this research discusses the GCPISC problem for a DX A/C system,in the DX evaporator of which,the dry-cooling and wet-cooling areas are time-varying.With the presented control method,the energy and thermal performances of the DX A/C system can be improved.With the solution,an open loop optimization for the control system is presented for reducing the energy demand of target building and maintain good thermal comfort.Lastly,the validity of the provided control strategy for a DX A/C system is demonstrated by simulation results.
The remainder of this content consists of five parts.The complex nonlinear dynamic modelling of a DX A/C system with uncertain parameters is presented in Section Ⅱ,followed by the design of a hierarchical control approach in Section Ⅲ.After that,the validity of the proposed strategy is demonstrated by numerical simulations in Section Ⅳ.Lastly,conclusions are summarized in Section Ⅴ.
Nomenclature:
A1Heat transfer area of the DX evaporator in the drycooling region,m2;
A2Heat transfer area of the DX evaporator in the wetcooling region,m2;
CaSpecific heat of air,kJ kg−1℃−1;
hfgLatent heat of vaporization of water,kJ/kg;
hr1Enthalpy of refrigerant at vaporisation inlet,kJ/kg;
hr2Enthalpy of refrigerant at vaporisation outlet,kJ/kg;
MlLatent load in the conditioned space,kg/s;
mrMass flow rate of refrigerant,kg/s;
QsSensible heat load in the conditioned space,kW;
Tz℃ Air temperature in the conditioned space,;
TdAir temperature leaving the dry-cooling region on air side,℃;
TsAir temperature leaving the DX evaporator,℃;
T0Temperature of the outdoor air,℃;
TmMixed air temperature,℃;
VVolume of the conditioned space,m3;
vfAir volumetric flow rate,m3/s;
Vh1Air side volume of the DX evaporator in the drycooling region on air side,m3;
Vh2Air side volume of the DX evaporator in the wetcooling region on air side,m3;
WzMoisture content of air-conditioned space,kg/kg dry air;
WsMoisture content of air leaving the DX evaporator,kg/kg dry air;
W0Moisture content of the outdoor air,kg/kg;
WmMixed moisture content,kg/kg dry air;
α1Heat transfer coefficient between air and the DX evaporator wall in the dry-cooling region,kW m−2℃−1;
α2Heat transfer coefficient between air and the DX evaporator wall in the wet-cooling region,kW m−2℃−1;
ρ Density of moist air,kg/m3;
δ Proportion of outside air entering inside,%.
II.PROBLEM FORMULATION
A.The Description and Dynamic Model of a DX A/C System
The DX A/C system of a general building is mainly composed of an air distribution unit and the DX refrigeration equipment,the simplified diagram of which is presented in Fig.1(for more details refer to [17],[18]).Assume that the system is operating at cooling mode.Other assumptions and the operating principles for the control system are given below [17].
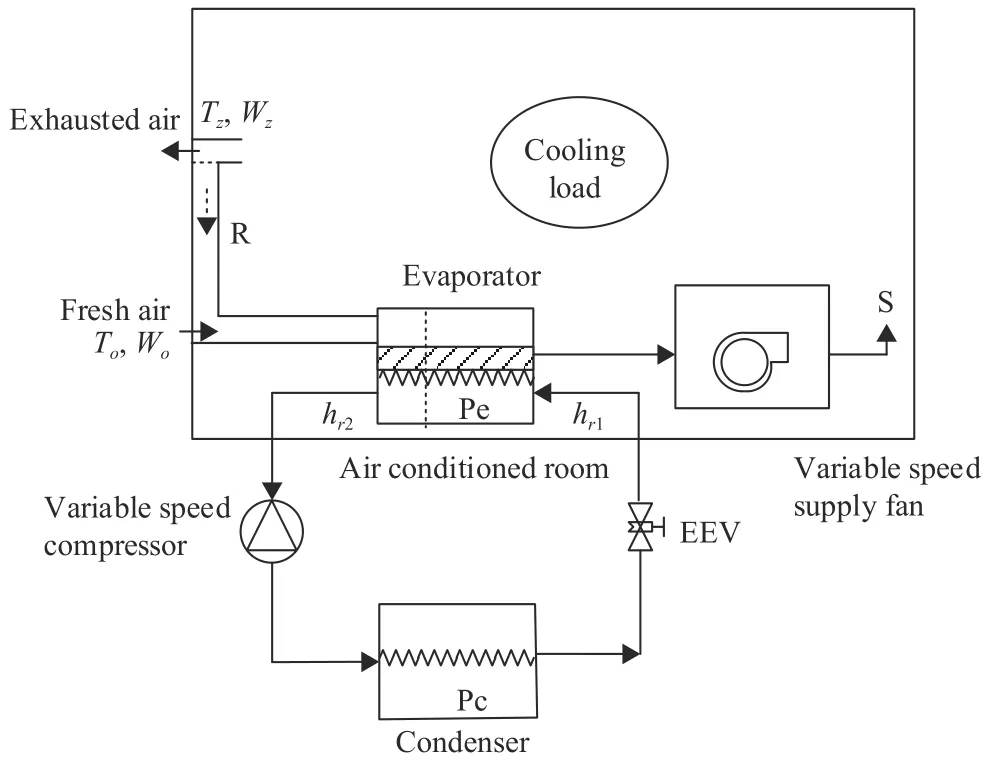
Fig.1.Simplified framework of a DX A/C control system.
1)A certain percentage,δ(0<δ<1),of outside air,is allowed to enter into the indoor unit and gets mixed with(1−δ)of the recirculated air to across the DX evaporator.
2)Plenty of air is mixed and gets conditioned inside the heat exchangers.
3)Heat quantity losses in air ducts are negligible.
4)The supply air enters the air-conditioned space to offset the indoor heat loads.
5)The air in the conditioned space is drawn by a fan.1−δ of the air is recirculated to the indoor unit and the remaining of it is recirculated by a fan.
Based on the principles of energy and mass conservation,the complex coupling dynamic model of the DX A/C system is built for control on the comfort indoor air temperature and relative humidity,etc.The model can be described by
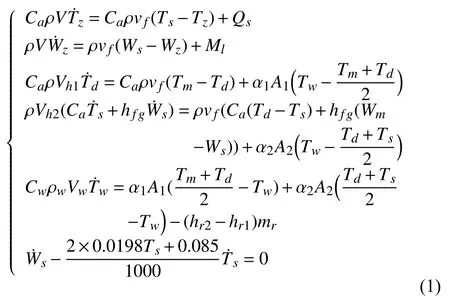
where α1and α2are expressed as follows [31]:
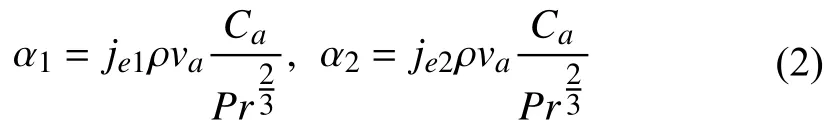
wherePris the Prandtl number,je1andje2are the Colburn factors,ahdvais the air velocity.
Remark 1:More details of the system models (1)can be found in [17] and [32].The system models (1),in which no outside air enters,were reported and experimentally validated in [32].This study will investigate the energy-efficient GCPISC problem based on these models.
The two regions on the airside of the DX evaporator,namely the dry-cooling region (sensible heat transfer only)and wet-cooling region (mixing latent and sensible heat transfer region),are shown in Fig.2.The coupling relationship between the two regions is that the outlet air characteristics of the dry-cooling region are the inlet air conditions entering the wet-cooling region.Hence,the space from pointA0toA1represents the dry-cooling region and the space from pointA1to theA2calls the wet-cooling region,they can be defined as
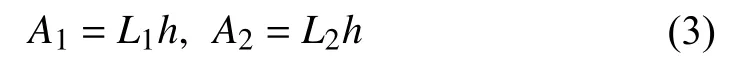
whereL1andL2are the length of the dry-cooling and wetcooling areas,respectively,and the total length of the DX evaporator isL0=L1+L2.his the height of the DX evaporator.
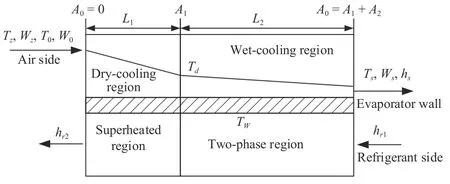
Fig.2.Simplified framework of DX evaporator.
In general,these parameters of the heat transfer coefficients,namely the dry-cooling regionA1and the wet-cooling regionA2(A2=A0−A1),are obtained from numerous experiments and remain unchanged during the operating process.However,due to the complexity of inherent operational characteristics between the dry-cooling and wet-cooling regions inside the DX evaporator and the difficulty of the measurement,the values keep time-varying as a DX A/C system during the operating process.Therefore,they are treated as uncertain parameters during the process.Here,is used to represent the varying part of,and the variations are assumed to be around the known nominal valueL1h.Then,the coefficient’s realized values are derived as
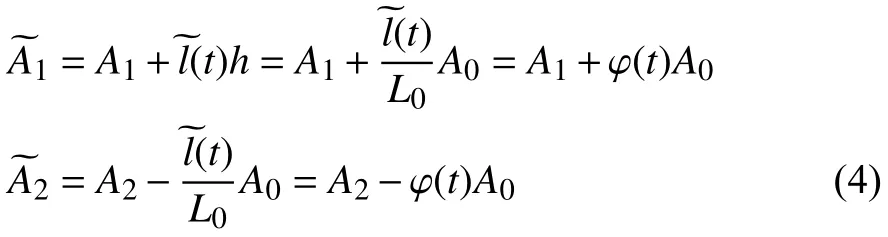
Based on (1)and (4),the state-space form of the DX A/C system can be compacted as

wherexTs,Tz,Td,Tw,Ws,Wz]T,u[vf,mr]T,andz[Qs,Ml,0,0,0,0]T.f1andf2are the nonlinear functions described as follows:

where indoor loadsQsandMlwere given in our previous work [18].
Remark 2:The dry-and wet-cooling areas of a DX A/C system are universal time-varying and uncertain during the system operation.This will influence the control performance of the DX A/C system if the uncertainty is not considered.This also results in inaccurate reflection of the physic inherent operating characteristic of the DX A/C system [19].The dryand wet-cooling regions were considered to be constant in[16],[17].In this study,the relevant parameters are considered to be time-varying and uncertain.Then,the operation stability is analyzed and the DX A/C system controllers with uncertain parameters are designed.
III.HIERARCHICAL CONTROL DESIGN
In this study,a hierarchical controller is designed to improve the energy efficiency of a DX A/C system and maintain good thermal comfort.The hierarchical controller includes an open loop control for minimizing the energy consumption of the DX A/C system and a closed-loop GCPISC for maintaining indoor air temperature and moisture content at their references.The framework of the proposed hierarchical controller is listed by Fig.3.

Fig.3.Simplified flowchart of the presented hierarchical control.
A.Open Loop Controller
An open loop controller is designed to schedule an optimal operation mode by minimizing the power consumption of the DX A/C system for the closed-loop periodically intermittentswitch controller.
The total power consumption model of the DX A/C systemPtotcan be calculated by

wherePe,Pc,andPfare the power consumptions of the condenser,compressor,and evaporator,respectively.They can be expressed by [33],[34]
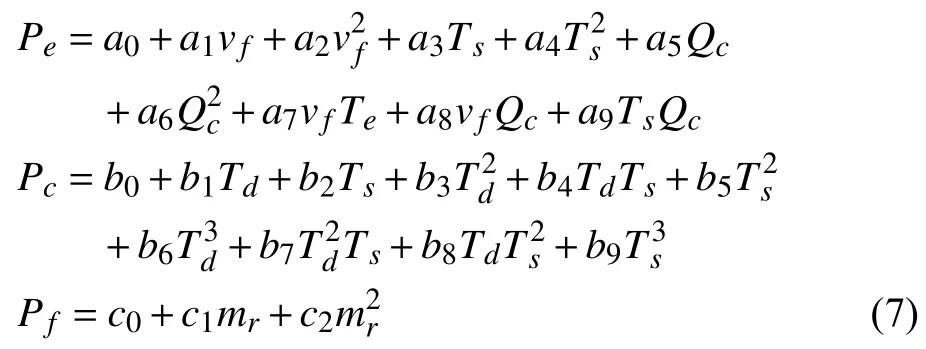
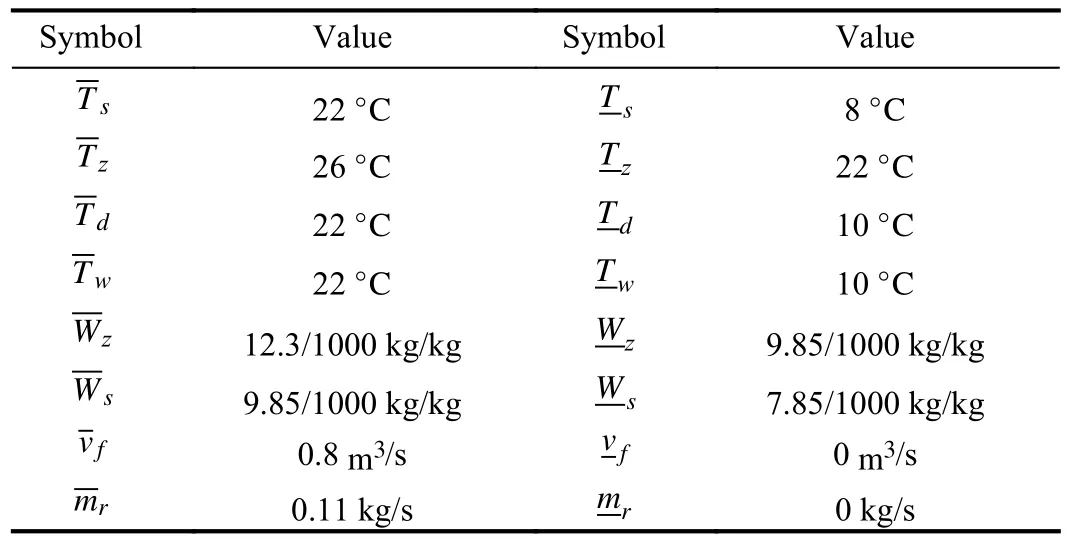
where the coefficientsai,bi(i=0,1,...,9),ci(i=0,1,2)can be determined experimentally by polynomial fitting [33],[34].Qcdenotes the building’s cooling load comprising sensible heat loadQsand latent heat loadMl.
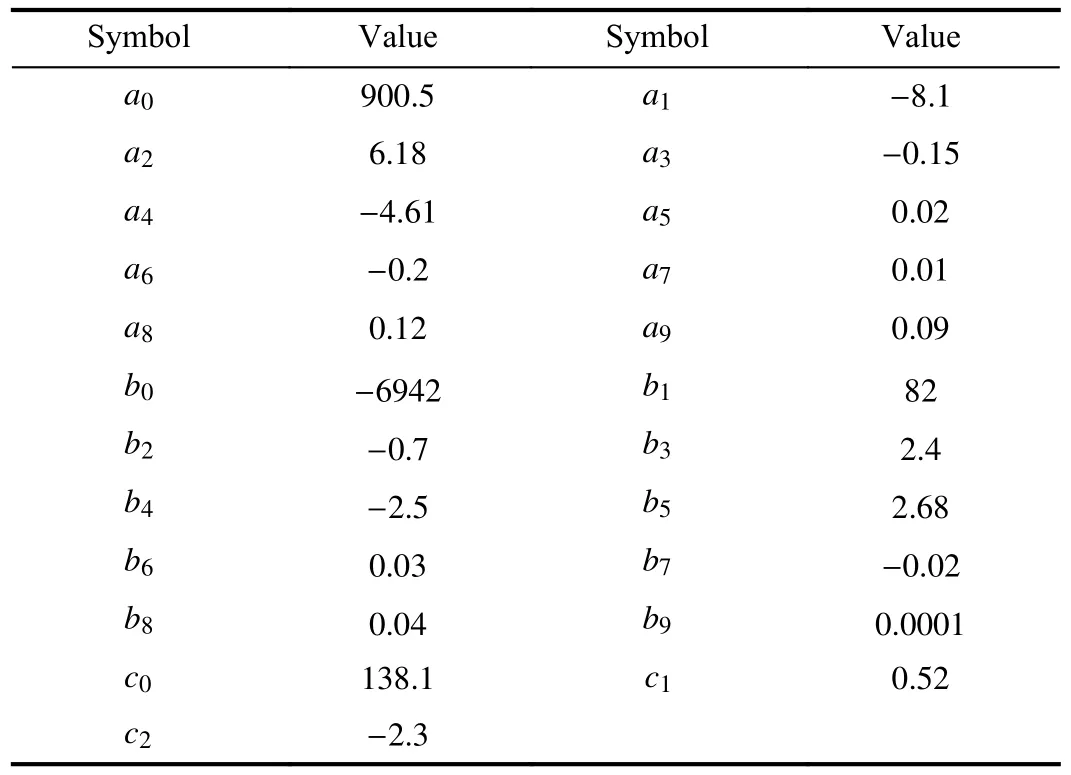
For the present open loop optimal control design,it is assumed that the system is at its steady state.Therefore,letanddenote the given setpoints of air temperature and moisture content of the conditioning room,which are selected according to a thermal comfort index.A steady state condition of the nonlinear model (5)is formulated as
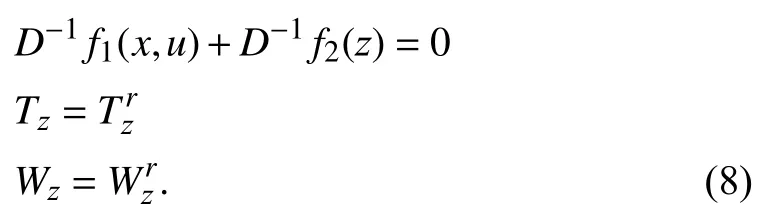
In our previous work [18],test results demonstrate that this open loop optimal controller is insensitive to the parametersA1andA2of the DX A/C system within any ranges of[aA0,bA0],where 0≤a,b≤1 anda≤b.Hence,A1=L1handA2=L2hare chosen in the equality constraint in (8).The uncertain parameters will be considered in the lower layer closed-loop control.
The operation of the DX A/C system is restricted by thermal comfort,physical characteristics,and operational limits,which are defined as follows.
(C3)Tw≤Td,which ensures that the air temperature crossing the DX cooling coils should be cold.
(C5)Td≤(1−p%)Tz+p%T0,Ws≤(1−p%)Wz+p%W0.The air temperature and moisture content of the mixed air formed by the outside return air crossing both the DX drycooling region and wet-cooling region can only drop.
Thus,the open loop energy-optimised scheduling of the DX A/C system can be formulated as a nonlinear static programming problem:minimize (6)subject to (8)and (C1)−(C5),which is concisely presented as follows:

Remark 3:In the optimization problem (9),the two equations can be referred to as the two equality constraints and set them at their setpoints.The obtained optimal steady state can be used as the trajectory reference by the lower layer closed-loop feedback controller to follow.The DX A/C system model is linearly approximated near the optimal solution calculated by the optimization problem (9).
B.Closed-Loop Controller Design
To facilitate the closed-loop controller design,the vectorsurandxrare used to represent the nominal control action and the steady state,respectively,which are obtained by the optimization formulation (9).Then,the control forceuris used to keep the DX A/C system at the steady state.e(t)=x(t)−xrand δu(t)=u(t)−urare defined as as the state and the control input vectors.From (1),the error dynamics can be linearized and represented by the following taking into account uncertain parameters:
wheree(t)[δTs,δTz,δTd,δTw,δWs,δWz]Trepresents the deviation defined bye(t)=x−xr,δu[δvfδmr]Trepresents the input deviation defined by δu=u−ur.δTz=Tz−,δWz=Wz−,δTs=Ts−,δTd=Td−,δTw=Tw−,δWs=Ws−,δvf=vf−,δmr=mr−are defined to be the derivations of the input and state variables from their steady states.andrepresent the steady state points of the state and input,respectively.The coefficient matricesAc(xr,ur),Bc(xr,ur)can be calculated as follows:

and the uncertain parameter matrix is △C=ΦE(t)H1,whereH1=diag{A0,...,A0}6×6,Φ andE(t)are defined as
To reduce the energy demand of the DX A/C system as well as to maintain good thermal comfort,a closed-loop periodically intermittent-switch controller (PISC)is presented in this study to stabilize the error dynamic model of the system (10)under the framework of the PISC strategy with the following form:

with the control gain for the supply fan designed as follows:
and the control gain for the compressor is designed below:
this controller is designed as a periodically switching control to avoid switching off/on frequently,damaging the compressor,and reducing the compressor’s power consumption.
In (12)and (13),the positive constantTis the controller’s control period,ϑ denotes the control width,K=[K1,K2]T,Ks=[0,K3]Tare the control gain matrix of controller to adjust the system to stabilize at a equilibrium point,andkis the number of control period.
Remark 4:The periodically intermittent controller (11)can be called a classic switching controller,the switching rules of which are only related to time.The control of the DX A/C system is periodic.Each operating period can be divided into two control intervals,namely“work time”and“idle time”.The supply fan speed controller is activated whent∈Θ1kand there is no control action on the system whent∈Θ2k.The compressor speed controller is switched at the two control intervals.Fig.4 is given to better clarify the periodically intermittent controller mechanism of the DX A/C system.

Fig.4.Simplified control mechanism of the presented periodically intermittent feedback controller [28].
With the design periodically intermittent-switch controller(11),the error dynamic model (10)is described as

To get the main results of this study,we will first introduce the definition and lemmas below.
Definition 1:The error dynamic model (10)is deemed to be exponentially stable if there are constant and positive scalarsTand ϑ,for ϑ for allt>0 and positive constantsMcand α.e(0)denotes the initial point of the error system (14). Lemma 1 [35]:Given any matricesandwith appropriate dimensions and a symmetric matrix Θ,then it concludes that the following condition: for all Σ(t) such that ΣT(t)Σ(t)≤I,if and only if there is a scalar ζ >0 to satisfy Lemma 2 (Schur complementary lemma [36]):Assume a real matrix as 1)Γ <0; 2)Γ11<0,Γ22−<0; 3)Γ22<0,Γ11−<0. For the DX A/C system,a GCPISC is designed making use of the Lyapunov stability,the optimal control theories,and the guaranteed cost periodically intermittent control method. The regulation control’s priority is to ensure the indoor comfort level.In addition,the DX A/C system is a piece of energy-intensive equipment,for which the energy consumption should be minimized.Therefore,a GCPISC strategy is considered in the lower layer to improve the indoor comfort level and minimize the total energy consumption.Accordingly,the following objective function is presented where whereSandRare the positive definite weighted matrices.The first part of the integration in (17)indicates the cumulative state deviation from its references corresponding to the indoor thermal comfort,and the second implies the cumulative energy consumption,which directly relates to the energy efficiency of the DX A/C system. The guaranteed cost intermittent-switch regulation control of a DX A/C system operation to be stated in this section is described below. Definition 2:For the error dynamic of the DX A/C system(10)and the guaranteed cost function (17),if there exists a periodically intermittent-switch control law δu(t)under the constraints in (C1)−(C5)and a positive constantJ∗such that the system outputs,namely indoor air temperature and humidity,are exponential to follow their desired references simultaneously,and the corresponding index of the guaranteed cost function (17)meetsJ≤J∗,thenJ∗is referred to as a guaranteed cost index and δu(t)is said to be a GCPISC law for the DX A/C system with the guaranteed cost function (17). The following theorems will give the sufficient conditions for the GCPISC of the DX A/C system to improve the energy efficiency and indoor thermal comfort. Theorem 1:For the given controller working periodTand control width ϑ,and considering the error dynamic model of the DX A/C system in the form of (14),if there exist positive scalars η,ζ1,ζ2,γ1,γ2,symmetric positive definite matrixM,and any matricesH,Hswith appropriate dimension to make the following inequalities hold: where Υ1=AcM++BcH++γ1M,andΥ2=AcM++BcHs+−γ2M,then,the periodically intermittentswitch controller δu(t)=F(t)e(t)is then obtained to ensure that the output commands of the DX A/C system can reach their desired references exponentially,and the error state satisfies where β=(ϑγ1−(T−ϑ)γ2)/T.Meanwhile,the corresponding guaranteed cost function (17)satisfiesJ<(γ1η/β)exp(βϑ),andJ∗=(γ1η/β)exp(βϑ)is a guaranteed cost value for the DX A/C system over a whole operation period. Proof:At first,to study the exponential stability of the error dynamic model of the DX A/C system (14),one can employ the Lyapunov theory and its function can be taken as wherePis a symmetric and positive definite matrix. Whent0+nT≤t where Ω1=PAc++PBcK+andPΦ=G. Inequality (28)holds if and only if holds. On the basis of Lemma 1,there exists a scalar constant>0to make (29)equivalent to We premultiply and postmultiply both sides of the inequality (30)by the term,we have By Schur complement,the inequality (31)holds if and only if the following inequality holds. Let both sides of (32)to premultiply and postmultiply by diag{I,ηI,I},one can obtain According to the inequality (28),one has fort∈[t0+nT,t0+nT+ϑ). Whent0+nT+ϑ≤t where Ω2=. By Lemma 1 and (20),and following (32)and (33),one obtains which implies fort∈[t0+nT+ϑ,t0+(n+1)T). Whent∈[0,ϑ),one has the following inequality based on(34) wheree0is initial point of the errore(t),and whent∈[ϑ,T),according to the inequality (37),one has Whent∈[T,T+ϑ) andt∈[T+ϑ,2T),one can obtain and Whent∈[nT,nT+ϑ),i.e.,(t−ϑ)/T Whent∈[nT+ϑ,(n+1)T),i.e.,t/T From (42)and (43),it concludes that for anyt>0 According to (26),we have where λmin(P) and λmax(P)denote the minimum and maximum eigenvalues of the positive definite matrixP,respectively. Based on (44)and (45),one obtains this implies that the error system is exponential stability and the indoor thermal comfort level is achieved. Hence,the periodically intermittent-switch controller can exponentially stabilize the DX A/C system at their optimal references of the indoor air temperature and moisture content under the state feedback control gainsK=HM−1andKs=HsM−1. Additionally,to analyze and obtain the upper bound of the guaranteed cost index function (17)over the whole time horizont∈[0,∞),we use (22)and (23),we have Fort∈[mT,mT+δ),using (22)and (23),we have According to (22)and (23),we have γ1≥γ2fort∈[mT+δ,(m+1)T)and it yields fort∈[mT,mT+δ),it also yields Based on (44),we have Lett→+∞ and according to the condition (24):eT(0)Pe(0)=V(0)≤η,one has Hence,the guaranteed cost function value is thenJ<(γ1η/β)exp(βϑ),and (γ1η/β)exp(βϑ)is the supremum guaranteed cost of the DX A/C system working over the total control horizon. ■ Remark 5:Theorem 1 gives a sufficient criterion to realize the exponential stability of the DX A/C system by the GCPISC law.This strategy is different from existing literature on DX A/C system control [17],[18],in which the output commands are continuous.Besides,this control scheme is also different from existing literature in term of genetic regulatory networks [37],uncertain nonlinear systems [38] and fuzzy time-delay systems [23],in which the guaranteed cost control laws are continuous.The proposed controller only operates the control action within the interval [t0+nT,t0+nT+ϑ)in each working periodT.The energy efficiency is improved when the proposed closed-loop GCPISC forces the DX A/C system to reach their trajectory reference [17].Also,this type of controller presents more advantages to energy efficiency improvement in comparison with [39] during short working time and the simulation results will illustrate this fact. It is noted that both the inequalities (19),(20),(22)and (23)are nonlinear matrix inequalities (NLMIs),and it is difficult to solve the control gain by the current algorithm.The NLMIs(19),(20),(22)and (23)can be converted to linear matrix inequalities (LMIs)in the following Theorem 2.For the proposed closed-loop control,the system variables should follow their physical conditions,thus,the exponential stability of the DX A/C system with input and state constraints is studied below. Theorem 2:For the error dynamic model of the DX A/C system with the control and state constraints in (C1)−(C5)under the periodically intermittent-switch controller (11),if there exist positive scalars γ1,γ2,η,ζ1,ζ2,positive definite matricesM,Γ1,Γ2,Z,positive definite diagonal matricesF,L,and any matricesH,Hswith appropriate dimensions satisfying: where Υ1=AcM++Γ1,Υ2=AcM+−Γ2,max,max,andEqdenotes theq-th column of an identity matrix,is theq-th entry ofur,then the intermittent-switch control input δu(t)=F(t)e(t)is obtained to guarantee that the output commands of the DX A/C system track the desired references exponentially,and the error dynamics satisfies where β=λmin((Γ1−(T−ϑ)Γ2)M−1/T).Meanwhile,the guaranteed cost function obeys thatJ<(γ1η/β)exp(βϑ),and the term (γ1η/β)exp(βϑ)is a supremum guaranteed cost for the DX A/C system operation. Proof:Let Γ1=γ1M,Γ2=γ2M,F=ζ1I,andL=ζ2I,then conditions (19)and (20)can be rewritten as LMIs (52)and(53).Then the inequality (21)is converted to (61).Let both sides of (22)to premultiply and postmultiply byM,and then multiply η−1I;according to the Schur complement principle,one can conclude that the nonlinear inequality (22)is transformed to then,the inequality (22)is converted to (55). Premultiply and postmultiply both sides of (23)byM,and then multiply by η−1I;by the Schur complement principle,the nonlinear inequality (23)is then transformed to By Lemma 1 and Theorem 1,the proposed periodically intermittent-switch controller can exponentially stabilize the DX A/C system to the optimal reference resulted from the upper layer control,and the error dynamic system satisfies(61). The control input constraints for the DX A/C system operation are given in (C4),namely,,which means that ∥uq(t)∥2≤max,whereuq(t)denotes theq-th entry ofu(t).The state variable constraints for the DX A/C system are provided in (C1)−(C3),namely,.It implies that ∥x(t)∥P≤max,where ∥x(t)∥P=xT(t)Px(t). By Lemma 2,the inequality (57)can be transferred to the following linear inequality According to the Cauchy-Schwarz inequality and the above inequality (64),one can obtain that theq-th row of the input vector is whereKqis theq-th row of the calculated control gain matrixKandis theq-th row of optimal control input reference. Letting both sides of (58)to premultiply and postmultiply diag{I,M−1} results in From inequalities (58),(59),(65)and (66),one can obtain which implies that the control constraint in (C4)holds. The bound of the state variable can also be used the Cauchy-Schwarz inequality as follows: By the Schur complement,it can be transformed to the following inequality: From inequalities (68)and (69),one has that which implies that the control constraints in (C1)−(C3)hold. Therefore,the proposed periodically intermittent-switch controller of the DX A/C system with an uncertain parameter can exponentially stabilize the indoor air temperature and humidity under the design control with control input and state constraints.Meanwhile,the corresponding cost function is obtained abounded asJ<(γ1η/β)exp(βϑ),where (γ1η/β)×exp(βϑ)is a guaranteed cost for the DX A/C system operation. ■ Remark 6:The optimal steady state is calculated by the upper layer open loop controller under state and input constraints.To ensure that the working point of the DX A/C system is operating within the feasible range and the energy efficiency improvement is achieved,this theorem should consider the control and state constraints when the proposed GCPISC stabilizing the error dynamic system with uncertain parameters. In practice,suitable controllers are necessary to optimize the upper bound on the control of DX A/C system so that the energy efficiency of the system and the thermal comfort of target building can be improved.According to Theorem 2,an optimization issue is developed to solve an optimal guaranteed cost controller to ensure the optimization of the upper bound on the control of DX A/C system below. Theorem 3:Considering the error dynamic model of the DX A/C system with the input and state constraints in (C1)−(C5)and the performance cost function (17),an open loop optimization problem can be formulated as follows: If a set of solutions (γ1,γ2,η,M,Γ1,Γ2,F,L,Z,H,Hs)can be obtained,it means that a local optimal guaranteed cost intermittent-switch controller to optimize the upper bound,δu∗(t)can also be obtained. Proof:According to Theorem 2,the feasibility of LMIs(52)−(60)implies that the thermal comfort of the target building can reach the desired level and the DX A/C system is stabilized to the steady state determined by the upper controller.In addition,sinceJ<(γ1η/β)exp(βϑ),the minimization of (γ1η/β)exp(βϑ)presents the superior control performance on the DX A/C system.It is noted that the optimization issue (71)ensures a global solution to the error dynamic model (14),which ensures to obtaining a local optimal solution to the original DX A/C system (1).If a feasible solution exists,a local optimal intermittent-switch controller δu∗(t)can be achieved to optimize the upper limit of the DX A/C system performance. ■ Remark 7:For the regulation control problems of the DX A/C system,the existing literature proposes the use of the traditional LQG [16] and the MPC method [17] to enhance control performance of the DX A/C system model with constant dry-cooling and wet-cooling areas.However,these optimal results may not sufficiently reflect the system’s actual operation with time-varying dry-cooling and wet-cooling areas.In contrast,the proposed optimal GCPISC approach is effective and can be applied to the dynamic system to improve the system performance on energy efficiency and thermal comfort.Therefore,the proposed control method is more effective and practical than the conventional control methods for the control of the DX A/C system.Except for this,the periodically intermittent-switch control of the DX A/C system based on guaranteed cost control is taken into consideration to ensure the minimization of energy consumption and improvement of indoor thermal comfort.Moreover,this optimization control problem can solve the optimal control gainsK∗=HM−1and=HsM−1in the controller (11)by minimizing guaranteed cost (γ1η/β)exp(βϑ). Remark 8:The proposed GCC is different from the famous linear quadratic regulator (LQR)control.GCC refers to mastering the best ability to achieve the intended purpose or specified purpose,so that it does not exceed the upper bound.LQR is linear,and its performance index function is the integral of the quadratic function of the state variable and the control variable,and the state variable constitutes the linear state feedback mode. The proposed optimization algorithm steps are given below. Algorithm 1A Nonlinear Programming (NLP)Algorithm to the Hierarchical Optimization Control Problems of the DX A/C System. Initialization:Given initial state valuesx(0)andu(0).The initial state values are chosen within their limitations. 1:Input the data of the outside air temperatureT0,moisture content,sensible heat,and latent loads. 2:The optimization objective function and the constraints in(9)are transformed to a standard form such that it could be expediently solved by the built-in functionfminconin MATLAB Toolbox: 3:Solve the above procedure (72). 4:Obtain optimal references,and. 5:Put the certain matrices and parametersΦ1,ϑ,Ac,Bc,S,R,xr,,T,H1. 6:The optimization objective function in (71)and the constraints in (52)−(60)are transformed to a standard form in(72). 7:Obtain optimal control gainsKandKs,and put the uncertain parameter φ(t)to the DX A/C system. 8:Solve the optimization guaranteed cost function (17)with the closed-loop feedback control system and constraints. 9:Obtain the tracking curves of air temperature and humidity. A case is studied to verify the effectiveness of the hierarchical controller designed for the DX A/C system with uncertain parameters,aiming at improving the energy efficiency of the system as well as ensuring indoor thermal comfort. This study considers an office room with a 77 m3volume space to be conditioned.Table I provides detailed information on the parameters related to the DX A/C system,Table II gives the figures of the variables associated with different constraints,and Table III shows the figures of the coefficients in (7)[33].The uncertain and time-varying parameter in the system is presumed to be φ(t)=|cos(t)|.The weighted matrices of the input error and tracking error in (17)are set to 0.5I2and 0.5I6,respectively,which are to balance the energy efficiency and thermal comfort levels. TABLE I PARAMETERS OF DYNAMIC SYSTEM MODEL TABLE II CONSTRAINTS OF THE DX A/C SYSTEM VARIABLES TABLE III COEFFICIENTS OF THE ENERGY CONSUMING MODEL Next,several scenarios are simulated to evaluate the effectiveness of the designed control strategy in different conditions. The validity of the designed control strategy is tested in different situations.In the simulation process,the setpoints of the indoor air temperature and moisture content are set to=24℃ and=11.35/1000 kg/kg,respectively. The process (9)is followed with the information given in Tables I and II.A unique set of steady states is provided and omitted here.The state and input matrices of the system (10),which are denoted byAcandBc,respectively,are then obtained.To verify the performance of the closed-loop GCPISC,the operating and working time are set toT=2 s and ϑ=1s,respectively.To improve the occupancy comfort of the target building to a certain level,several constraints need to follow.In the simulation,the disturbance is taken into account to test the closed-loop system’s robustness.The initial values of the state variables are set to 23℃,23℃,23℃,15℃,12.44/1000 kg/kg,and 15.5/1000 kg/kg,respectively.The initial values of the input variables are set to 0.It is currently assumed that the indoor temperature is 30 ℃ and the moisture content is 15.5/1000 kg/kg. With the LMIs (52)−(60)in Theorem 3,the best control gainsK∗andcan be obtained with the LMI Toolbox from MATLAB software.The DX A/C system can then follow the best trajectory reference provided by the upper-layer open loop energy-optimized controller. The performance of the proposed GCPISC controller is displayed in Fig.5.The figure indicates that the indoor air temperature and relative humidity of the conditioned room can reach their desired setpoints simultaneously by controlling the speeds of the indoor unit supply fan and the compressor through the closed-loop GCPISC.Once the two factors of the conditioned room reach their setpoints,which are set to 24 and 60%,they will stay at the setpoints afterwards.For 36 air temperature and 18.5 kg/kg moisture content,it can be seen from Fig.6 that the proposed controller can still force the indoor air temperature and relative humidity of the conditioned room to reach their desired setpoints.For the control on occupancy comfort,the portions of the cooling loads are commonly uncertain.Hence,the disturbance factor is considered in the simulation test.It is observed from Fig.7 that the indoor air temperature and relative humidity can still reach their setpoints taking the disturbance factor into account,which implies that the GCPISC can ensure the reference following capability.Fig.8 shows that the indoor air temperature and relative humidity of the closed-loop system are capable of reaching their desired setpoints with the proposed controller whenT=2 s and ϑ=1.2 s.Therefore,the proposed GCPISC controller can effectively improve the thermal comfort of the target building by controlling the compressor and the supply fan speeds. ℃ ℃ The comparison between the proposed GCPISC method and other control strategies is analyzed in this section to verify the performance of the proposed control strategy. The first approach is the proposed GCPISC with the control parameters set toT=2 s and ϑ=1.4 s,referred to as C1.The second approach is the intermittent-switch control method[28] with the control parameters set toT=2 s and ϑ=1.4 s,referred to as C2.Furthermore,guaranteed cost feedback control proposed in [39] is one of the effective continuous control methods and is referred to as C3.This control strategy is capable of handling uncertain parameters,guaranteeing occupancy comfort,and improving energy performance.For comparison,the three control methods are employed to conduct the simulations independently under the same conditions.Specifically,the target of the air temperature is=24℃ and that of the moisture content is=11.35/1000 kg/kg.The initial points of them areTz=30℃ andWz=15.5/1000 kg/kg.The total simulation time is 1 hour. Fig.5.Reference regulation of indoor temperature and moisture content. Fig.6.Reference regulation of indoor air temperature and moisture content under different initial point. Fig.7.Reference regulation of indoor air temperature and moisture content under disturbance factor. Fig.8.Reference regulation of indoor air temperature and moisture content under different control width. To assess control performance,some quantitative targets on energy performance are discussed.The energy usage is calculated approximately byE=,whereTfis the total simulation time.In Table IV,the total energy consumption with different controllers is summarized.One can observe that the GCPISC strategy performs better than the continuous control ones considering the total energyconsumed and the control time. TABLE IV COMpARISON OF DIFFERENT CONTROL METHODS In summary,the proposed GCPISC approach can effectively reduce the energy demand and the controller's working time by sacrificing part of the transient processability.The proposed control strategy is therefore satisfactory. In this study,we proposed an open loop optimization control and a closed-loop optimal guaranteed cost periodically intermittent-switch control (GCPISC)for a DX A/C system with uncertain parameters and control and state constraints to improve both indoor thermal comfort and energy efficiency.With the guaranteed cost control and periodically intermittentswitch control techniques,a GCPISC technique is obtained.In accordance to the Lyapunov stability theory and the obtained GCPISC technique,closed-loop optimal GCPISC laws are designed with linear matrix inequalities (LMIs).The indoor air temperature and relative humidity can reach the optimal references calculated by the open loop controller.Meanwhile,the guaranteed cost bounded for the system is optimised and obtained.Through the way of adjusting the cost function’s weighting matrices,a trade-off between the comfort level and the system’s energy performance can be achieved.Numerical examples demonstrate the feasibility,advantage,and effectiveness of the presented control approach. In this work,the GCPISC controller is based on the Taylor based linearization system,which may result in some loss of accuracy in the DX A/C system’s performance.In future work,we will study a decoupled control method to decouple the nonlinear DX A/C system,which results in an input-output linear system.Then an optimal GCPISC controller for energy performance improvement will be proposed based on an input-output linear system.

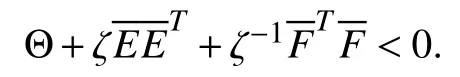

C.Guaranteed Cost Intermittent-Switch Control
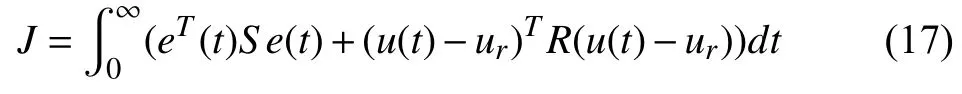

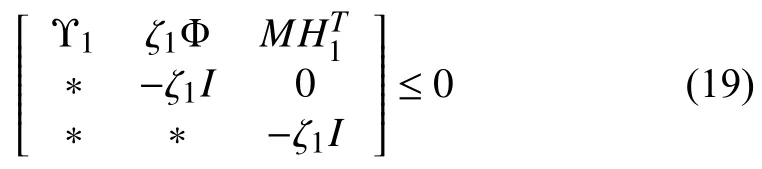





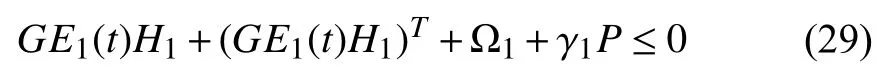




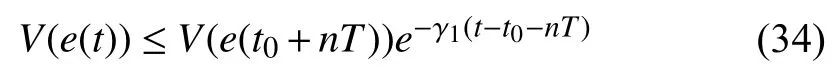
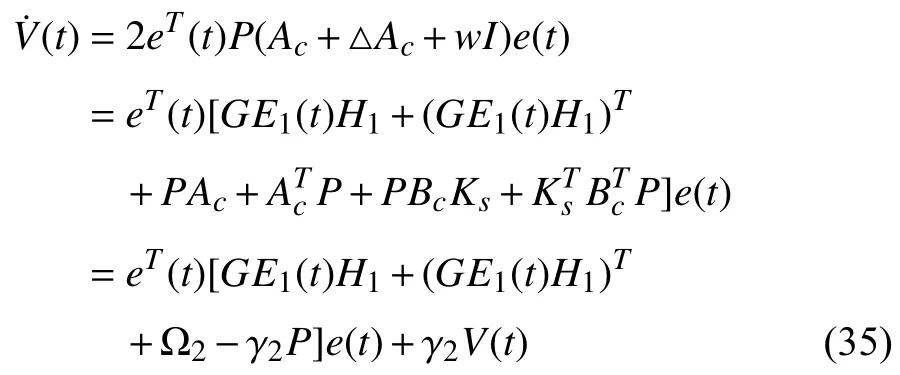

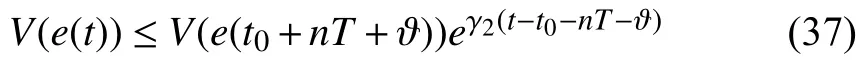


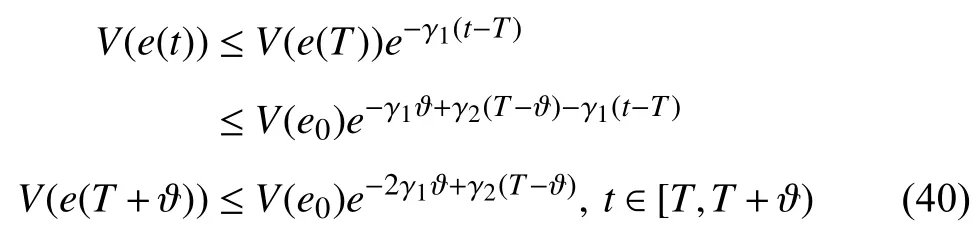

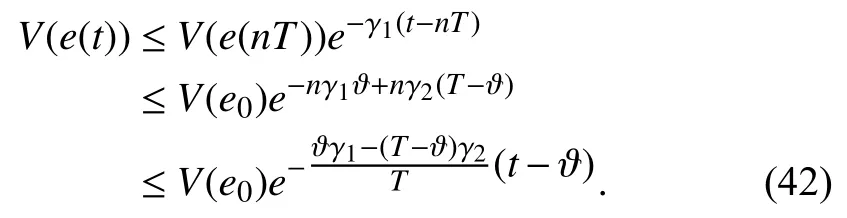
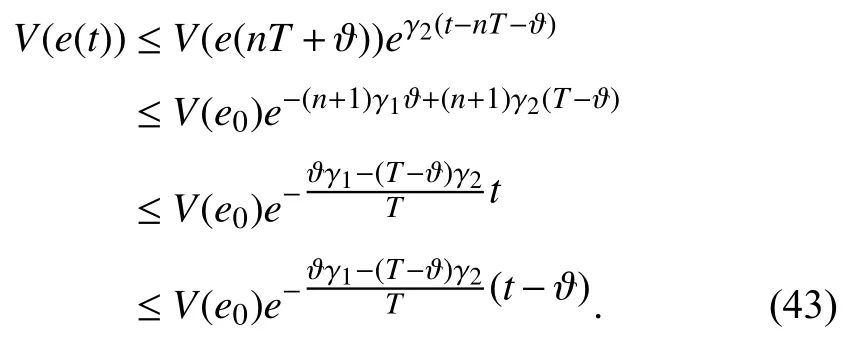






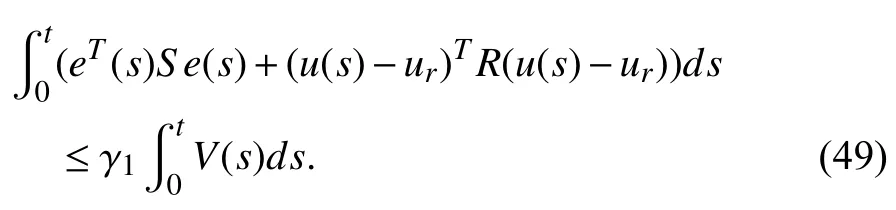




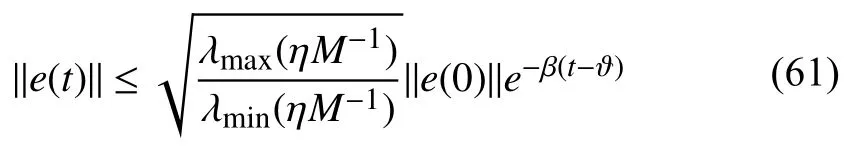
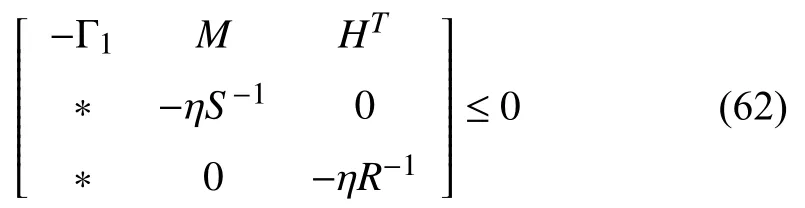




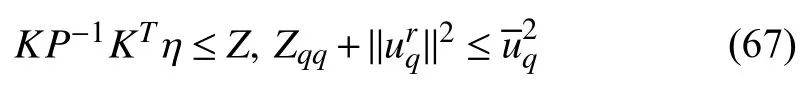



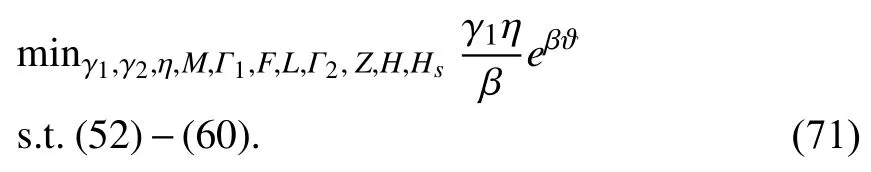
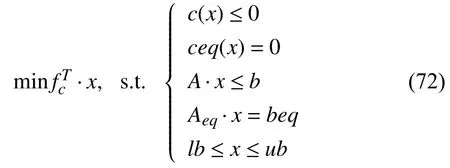
IV.NUMERICAL EXAMpLES

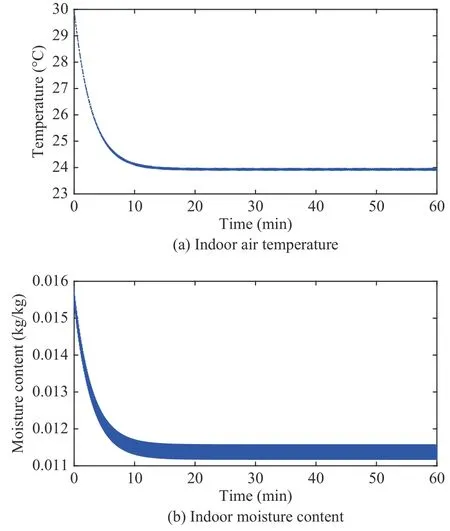
A.Comfort Performance of the Proposed Control Scheme
B.Comparisons With Previous Control Strategies




V.CONCLUSIONS
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Decentralized Resilient H∞ Load Frequency Control for Cyber-Physical Power Systems Under DoS Attacks
- Adaptive Consensus of Non-Strict Feedback Switched Multi-Agent Systems With Input Saturations
- A Novel Product Remaining Useful Life Prediction Approach Considering Fault Effects
- A New Safety Assessment Method Based on Belief Rule Base With Attribute Reliability
- Enhanced Intrusion Detection System for an EH IoT Architecture Using a Cooperative UAV Relay and Friendly UAV Jammer
- Data-Driven Heuristic Assisted Memetic Algorithm for Efficient Inter-Satellite Link Scheduling in the BeiDou Navigation Satellite System
