Decentralized Resilient H∞ Load Frequency Control for Cyber-Physical Power Systems Under DoS Attacks

Xin Zhao,Suli Zou,,and Zhongjing Ma, Senior

Abstract—This paper designs a decentralized resilient H∞ load frequency control (LFC)scheme for multi-area cyber-physical power systems (CPPSs).Under the network-based control framework,the sampled measurements are transmitted through the communication networks,which may be attacked by energylimited denial-of-service (DoS)attacks with a characterization of the maximum count of continuous data losses (resilience index).Each area is controlled in a decentralized mode,and the impacts on one area from other areas via their interconnections are regarded as the additional load disturbance of this area.Then,the closed-loop LFC system of each area under DoS attacks is modeled as an aperiodic sampled-data control system with external disturbances.Under this modeling,a decentralized resilient H∞ scheme is presented to design the state-feedback controllers with guaranteed H∞ performance and resilience index based on a novel transmission interval-dependent loop functional method.When given the controllers,the proposed scheme can obtain a less conservative H∞ performance and resilience index that the LFC system can tolerate.The effectiveness of the proposed LFC scheme is evaluated on a one-area CPPS and two three-area CPPSs under DoS attacks.

I.INTRODUCTION

WITH the developments of smart grids,advanced sensors,communication and control techniques have been widely applied in the operation of power systems,where traditional power systems are gradually integrated with information control equipment and communication and sensor networks to evolve as cyber-physical power systems (CPPSs)[1].To operate multi-area CPPSs smoothly,the LFC operation is widely used to restore the balance between generation and load in each control area for maintaining system frequency and power interchanges with other areas at scheduled values[2].Thus,the LFC design of CPPSs has drawn lots of attention in recent years because there exists some hot issues in the cyber layer such as network-induced delay [3]–[5],communication bandwidth constraints,cyber attacks [6]–[9],and so on.In the framework of networked control system,sampled-data based LFC is often implemented such that the system contains a continuous-time process and discrete-time controller.For sampled-data LFC scheme,one way is to design it in continuous-time mode,and then implement it in a sampled-data manner,such as in,H∞control method [10],the pole assignment method [11],and unified PID turning scheme for LFC based on internal model control method [12].But,the aforementioned LFC schemes are effective for a small enough sampling period.Another method is to design sampled-data LFC scheme based on the discrete LFC system,for example,event-triggered sliding mode LFC scheme [13],decentralized sliding mode LFC design considering time delay and wind power [14],and digital PID-type LFC design [15].These results are obtained by regarding the sampling period as a discrete step.However,in practical LFC operations,the discrete LFC system may be infeasible to restore the real dynamic of the original system because the sampling period is generally set in the interval [2 s,4 s] [2] under which the discrete period cannot satisfy Shannon sampling principle when time constants lying in internal [0.08 s,0.3 s] in hydrothermal power system [2].

In order to avoid the two shortages above,an input-delay method is proposed to investigate the control design of sampled-data systems for avoiding discrete distortion [16].As an improvement,a looped-functional method is proposed in[17] and further extended in [18].Based on this method,the stability of LFC systems with both sampling and transmission delay is analyzed for different given PI controllers [19],and a robust LFC design considering both sampling period and transmission delay is proposed in [20].Considering the penetration of wind power,a sampled-data and fast LFC scheme is proposed for multi-area power systems in [21],which focuses on the inner stability of LFC systems without taking the effects of load disturbances into account.Especially,for a typical sampling period of [2 s,4 s] in the practical LFC operations,it is necessary to develop sampleddata LFC schemes which considers sampling information and load disturbances.

In the cyber layer,when open communication infrastructures are employed to complete the information exchange between power plants and LFC center,it has the benefits of low cost and high flexibility [22].However,open communication networks are vulnerable to malicious attacks from adversaries,in which the cyber attacks generally are classified as deception attacks and denial-of-service (DoS)attacks [23].Deception attacks comprise the trustworthiness of transmitted data,while DoS attacks can block communication transmissions through injecting a large volume of useless data to deliberately consume the limited resources,which leads to the absence of sampled data [24].Representative accidents worldwide are highlighted as reports on multiple power blackouts in Brazil,the SQL Slammer worm attack on the Davis-Bessel nuclear plant,the StuxNet computer worm,and various other industrial security incidents [25].Thus,it is significant to study how to alleviate the impact of cyber attacks while ensuring that the power system operates stably.Recalling some existing results:some comprehensive surveys can be referred to control synthesis under cyber attacks[25]–[27].The running of DoS attacks are assumed to be periodic in [28],and obey Markov chain in [29].To relax these strong assumptions,a general model is established by constraining DoS frequency and duration for designing sampling logic to retain closed-loop stability via a given stabilizing controller [30].For designing resilient stabilizing controller against DoS attacks,an aperiodic sampled-data model on the duration bound of DoS is proposed in [31].Recently,[32] proposed a discrete switching system-based decentralized LFC scheme considering both the duration and frequency of DoS attacks.As discussed before,the discrete switching system may not restore the real dynamic of the continuous LFS systems because it treats the sampling period as a discrete step.In order to improve communication efficiency,different event-triggered LFC schemes for multiarea power systems are widely investigated under cyber attacks,such as energy-limited DoS attacks [6],[33],deception attacks [34] and hybrid cyber attacks [35].The above event-triggered LFC schemes generally consider a sampling period less than 1 s,which cannot match the requirement in practical LFC operations.Moreover,these results are implemented in centralized LFC schemes,which causes higher computation complexity and communication burden along with more areas or more generation units in each area.

Based on the above observations and discussions,this paper investigates decentralized resilientH∞LFC schemes for CPPSs under energy-limited DoS attacks.Firstly,similar to[20],the impact on one area from other areas via their interconnection are regarded as the additional load disturbance of this area,and a decentralized LFC strategy can be applied for each area.Secondly,we model the closed-loop LFC model as an aperiodic sampled-data system.Thirdly,according to[17],we propose a novel loop functional to obtain new bounded real lemma (BRL)and controller design method.Then,a decentralized resilientH∞LFC scheme is presented with guaranteedH∞performance and resilient to DoS attacks.Finally,the effectiveness of the proposed scheme is evaluated based on a one-area CPPS and two three-area CPPSs under DoS attacks.

The main contributions of this paper are summarized as

1)In the presence of DoS attacks,the closed-loop LFC model of each area is modeled as an aperiodic sampled-data system with external disturbances.

2)A transmission interval-dependent looped functional is proposed to obtain new BRL and controller design method against the above modeled system,and it can improve the results in [21] and not involve free matrices from the use of inequality by comparing with [31].

3)Based on the obtained theoretic results,a decentralized resilientH∞LFC scheme is presented in this paper.By regulating the parameters onH∞performance index or the maximum count of continuous data losses,the designed controller can maintain the stability of system frequency with guaranteedH∞performance and enhanced resilience to DoS attacks.

4)One-area and two three-area CPPSs are employed to verify the effectiveness of the proposed method,in which the controllers designed by the proposed method can ensure the stability of frequency with more resilience to DoS attacks than that of [6],[21] and have better control performance than that of [32].

The remainder of the paper is organized as follows.Section II gives the LFC dynamic model of each area under energylimited DoS attacks.H∞performance analysis method and controller design is presented in Section III.Some case studies with the analyses and simulations are provided in Section IV.Section V summarizes this article.

Notations:Throughout the paper,the superscript“T”represents the transposition of a matrix or vector.Iis the identity matrix of appropriate dimensions.N is a non-negative integer,and R≥0is a real number larger than or equal to 0.⎿x」stands for the maximum integer smaller thanx.The symbol“⋆ ”in a symmetric block matrix represents a term induced by symmetry.The notation(Sn×n)is an×nof symmetric positive definite (symmetric matrix)matrix space.The notation Rm×nis anm×nreal matrix space.The diag{···} and col{···}denote a block diagonal matrix and a block-column vector (matrix),respectively.H e(X)=XT+X.

II.PROBLEM FORMULATION

AN-area CPPS is considered in this paper,as shown in Fig.1.Fig.1 gives the LFC topology of each areai∈N ≜{1,...,N},wherein the physical layer consists ofngenerators,loads,and tie lines that exchange power with other areas,and the cyber layer consists of sensor &samplers (SA),the communication network,LFC center and zero-order-hold and actuators(ZOHA).

In such multi-area CPPS,the goal of the LFC operation is to maintain the system frequency and achieve the scheduled tieline power exchange,which is achieved in the network-based control framework.However,the open communication network may suffer from cyber attacks by adversaries in CPPS.In this paper,we mainly focus on DoS attacks that may occur in networks connecting SAs to LFC center.For the purpose of simplicity,we ignore the network-induced delays due to their tininess when compared to the sampling period 2 s–4 s of signal transmission in the practical LFC operations[36].

A.Dynamic Model of Multi-Area CPPS

The dynamic model of the multi-area CPPS is described by the state-space equations below [21]:

Fig.1.Control structure of area i.

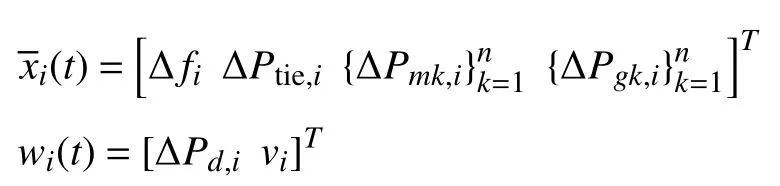
where ∆fiand ∆fjare the frequency deviations in areasiandj,respectively;∆Ptie,iis the total tie-line power exchange with the neighboring areas;∆Pmk,iand ∆Pgk,irepresent thek-th generator’s mechanical power output increment and the valve position difference,respectively.∆Pd,irepresents the load disturbance andTijis the tie-line synchronizing coefficient between areaiand areaj.virepresents the impacts on areaifrom other areas via their interconnections.The notation ∆ is used to indicate a deviation from the steady state.

The parameters in (1)are specified as follows:

with

For the dynamic model above,the technical assumption is implied as follows.

Assumption 1:For each control area,vi,i.e.,the power exchange involving the state of other areas,is treated as an additional load disturbance exerted on areai.

Remark 1:In the construction of LFC dynamic model of[4],[33],the connection between areas is regarded as a state of the multi-area LFC model to design centralized LFC scheme.But,large-scale systems will generate high-dimension state variables and face computational difficulties.By applying Assumption 1,only local variables are needed for LFC design so that decentralized control mode for each area becomes feasible.Also,similar technical assumption can be found in [5],[37].

For the LFC operation,in order to maintain the system frequency stability and achieve the scheduled tie-line power exchange,the area control error (ACE)of each area is generally defined as a linear combination of the deviations of the frequency and the tie-line power exchange

where βirepresents the frequency bias factor which equals

For achieving the state-feedback control,we introduce the integral of A CEito the state,and define it as

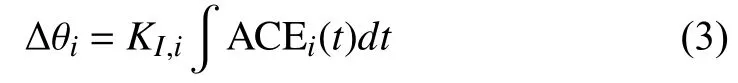
whereKI,iis assumed as a known integral gain of areaifor forcing the zero steady state of ∆fiand ∆Ptie,i.Then,by introducing ∆θito the state variablein (1),we have following new state and output:

where λ1,iand λ2,iare chosen coefficients.Based on (4),it gives a dynamic model of the LFC system

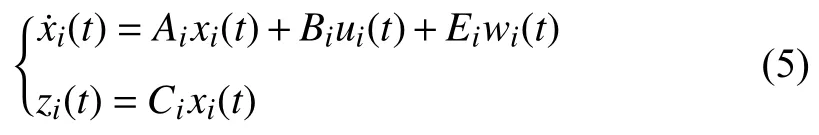
where

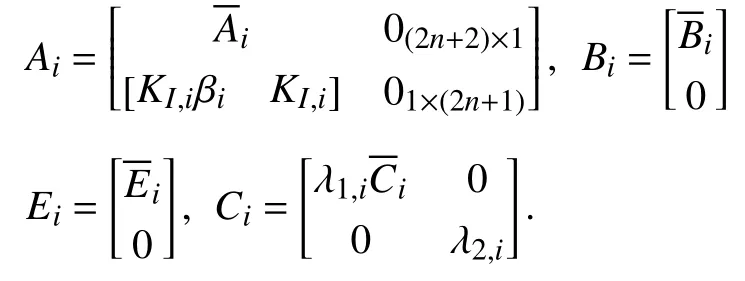
B.Sampled-Data LFC Model Under DoS Attacks

In continuous-time control mode,xi(t)is directly used to compute the control signal by the controller.However,from the view of actual systems,the LFC scheme usually works in sampled-data mode under network environment that the feedback and control signals are updated with sampling periodT0∈[2 s,4 s][2].Hence,we apply the same sampling periodT0here.As shown in Fig.1,xi(t)is measured and sampled by SAs and generate a sampled sequence S1={s0,s1,s2,...,sk,...},k∈N,in whichskequalskT0.Then,the state information of sampling instants are transmitted by communication channels from remote terminal units (RTUs)to the controller where the control signaluiis computed.The role of ZOHA is to implement the control signaluito continuous-time power systems.

As for security in CPPSs,some malicious attackers may launch cyber attacks in communication networks to interfere with the operation of power systems and even lead to its collapse.As a representative of cyber attacks,DoS attacks may block communication transmission with a large volume of useless data to deliberately consume the limited resources,such as CPU cycles,network bandwidth,or packet buffers,and further affect the control/operation process of the system[25].Suppose that the cyber layer is subjected to DoS attacks in the LFC process.It prevents the sampling data packets from being transmitted from the RTUs to the controller,resulting in unreliable control without enough data.Denote by Ξ(0,t)the total interval where the communication is denied due to DoS attacks.Thus,if the sampling instantssk∈Ξ(0,t),the corresponding sampling data packets can not be received by controller.Let S2={t0,t1,...,tk,...}⊆[0,t),k∈N denote the set of sampling instants at which data packets are successfully transmitted.By the definition of S1and S2,S2⊆S1.Therefore,DoS-induced data losses betweentkandtk+1are denoted as

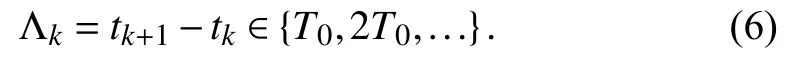
There may exist DoS attacks betweentkandtk+1.Iftk+1−tk=T0,no DoS attacks occur or a DoS attack occurs but is not malicious.Otherwise,there exists DoS attacks during the time interval [tk,tk+1);see Fig.2 as an example.In Fig.2,we denote by thehr∈Nthe time sequence of DoS attacks fromofftoon,and ζr∈R≥0the duration for therDoS interval.Then,the set of sampling instants{s2,s3,s5,s7−s10,s13,s14}belongs to DoS attacks interval Ξ(0,15T0),then data packets at these instants are not received by the controller.Within the interval [0,15T0],the maximal count of instants of data losses is 4 and the minimal count is 1.Also,Λk∈{T0,2T0,3T0,5T0}.

Since the DoS attacks are stealthy and energy-limited [24],[33],without loss of generality,the following assumption is given.

Assumption 2:For the stealthy and energy-limited DoS attacks,the maximum count of continuous data losses induced by DoS attacks is smaller than or equal to Θ where Θ is an integer.

Under Assumption 2 and by (6),we have

If Θ=0,no DoS occurs betweentkandtk+1.

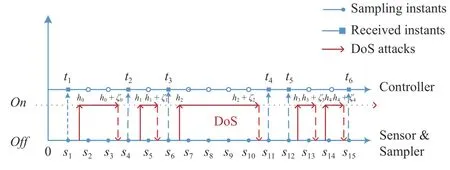
Fig.2.Data transmission under DoS attacks.

Remark 2:Similar to the modeling in [31],it is seen as a nonuniform sampling process with bounded interval when DoS attacks exist in the communication channels.Due to their stealth and energy limitation,attackers cannot launch frequently between theoff/onstatus of DoS attacks,and its duration ζrshould be bounded [30].Hence,we utilize Θ to constrain the DoS-induced continuous data losses.Otherwise,an alarm may be triggered for detecting attacks.The setups are different from those of [28],[29],in which DoS attacks are assumed to satisfy the periodic or probabilistic distribution.

Based on the above analysis,a sampled-data state feedback controller is designed for (5)

whereFiis the sampled-data LFC gain of areai.

Combining (5)and (8),the closed-loop LFC model of each area is obtained for allt∈[tk,tk+1),k∈N

It is seen clearly that the state of LFC system is periodicallyT0,while under DoS attacks,the resulted closed-loop system is an aperiodic sampled-data control system that involves both a continuous-time dynamics and a sampled-data controller.Note that the resilient controller designed in (8)could maintain the frequency and the power exchange among different areas at the scheduled values undergoing disturbances and DoS attacks.

In the following,we propose anH∞performance analysis method for the closed-loop LFC system (9)under DoS attacks,and design the LFC gainFiof each area such that

1)For given sampling intervalT0,based on energy-limited DoS attacks characterized by Θ,the system (9)withwi(t)=0 is asymptotically stable.

2)Under the zero initial state condition,for any sampling interval smaller than or equal to a given upper bound(Θ+1)T0and any nonzerowi(t)∈L2[0,+∞),the inequality

holds if theH∞performance index,denoted by γ,is as small as possible.

III.RESILIENT H∞ LOAD FREQUENCY CONTROL SCHEME

This section proposes a transmission interval (Λk)-dependent looped functional to investigateH∞performance and design controller for LFC system (9).TheH∞performance analysis,resilientH∞controller design,and the procedure of resilientH∞LFC scheme are specified in Sections III-A–III-C,respectively.The LMI technique and the looped functional method are leveraged to obtain the main results in this paper.

Note that the section involves the transmission interval that corresponds to the Λkof an aperiodic sampling-data LFC system (9).Specifically,the Λkis the interval between any two consecutive transmission time instants in the set S2.

A.Transmission Interval-Dependent H∞ Performance Analysis

The following new BRL is obtained by employing a Λk-dependent looped functional method and presents the relationship between the transmission interval and theH∞performance index γ.

Theorem 1:Consider the following class of sampled-data systems with bounded transmission intervals:

for allt∈[tk,tk+1),k∈N with a bounded interval

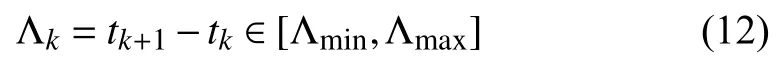
where Λminand Λmaxare two scalars satisfying0<Λmin≤Λmax<+∞.For some given scalars Λmin,Λmax,γ and a matrixF∈Rp×r,if there exists real matrices,Qi∈R2r×4r,S∈R2r×2r,Z∈S2r×2r,X∈Rr×r,R1,,Y1∈Rr×randY2∈R5r×r,such that,forΛk∈[Λmin,Λmax]

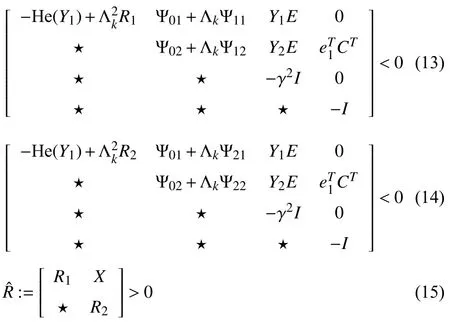
whererandpare the dimension number ofAand the column number ofB,respectively,and Ψ01,Ψ02,Ψ11,Ψ12,Ψ21,Ψ22are written in Appendix B.Then the system (11)is asymptotically stable with γ against nonzero disturbance for any sampling intervals belonging to [Λmin,Λmax].

Proof:The proof of Theorem 1 is shown in Appendix B. ■

For a given controllerFiand a sampling periodT0,the system (9)is asymptotically stable with γ if the conditions of Theorem 1 are satisfied under the set Λmin=T0and Λmax=(Θ+1)T0.Thus,one provides aH∞performance analysis method for LFC system of each area under load disturbance and energy-limited DoS attacks.

Remark 3:Conditions (13)and (14)cannot be directly solved by the LMI toolbox of MATLAB since they depend on DoS-induced interval Λk.Moreover,Λkappears in a quadratic form and the-dependent terms arediag{Rl,0,0,0}≥0(l=1,2).By Lemma 1 in Appendix A,both (13)and (14)hold for Λk∈[Λmin,Λmax] if<0,<0,<0 and<0.

Remark 4:Compared with related results in the literature,Theorem 1 features:

1)The looped functionalV(t)fully utilizes the two-sided information fromx(tk)tox(t)andx(t)tox(tk+1)as well as its integrationandto reduce the conservatism of BRL,while only one-sided information is utilized in [21].

2)A Λk-dependent looped functional,sayV4,is proposed to cater for estimating the integral terms ofby simple inequalities.Different from those of [18],[21],[31],no freematrix-based inequalities or techniques are introduced for reducing computation complexity.

3)For the case Λmin=Λmax,i.e.,no DoS attacks,the maximum constant sampling interval could be obtained such that the system (9)is asymptotically stable under theH∞performance γ.

4)Compared to the use of Lapunov-Krasovskii functional(LKF)and discontinuous Lyapunov functional (DLF)in [6],[33],the looped functional method has less conservatism than LKF and DLF as seen in [17],[26].

If we only consider the inner stability of the equilibrium point of (11),which is equivalent to the origin’s stability withw(t)=0,the following stability condition is obtained.

Corollary 1:For given Λmin,Λmax,andF,the system (11)is internally stable for Λk∈[Λmin,Λmax] if the following inequalities hold:

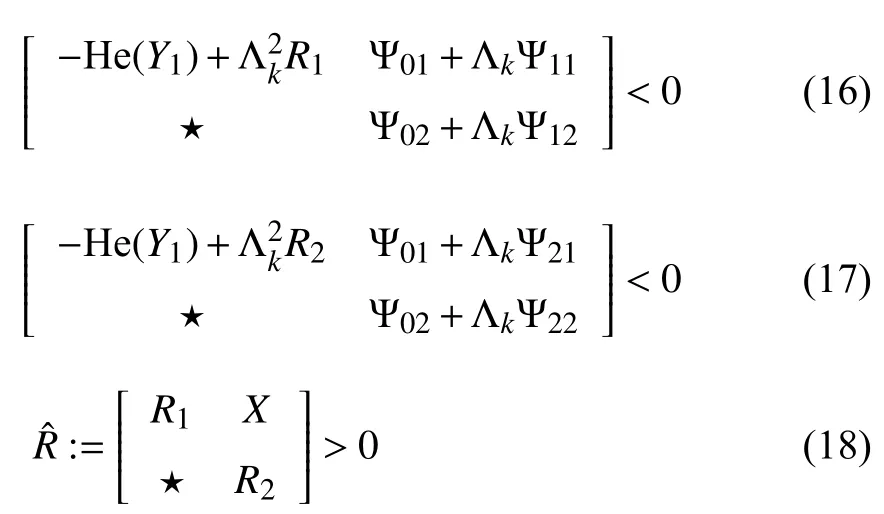
where all variables are the same as Theorem 1.The feasibility of (16)–(18)holds if (13)–(15)are feasible,thus the system(11),withw(t)=0,is asymptotically stable.

For the closed-loop system equipped with a designed controllerF,the minimalH∞performance index γmincan be derived from the conditions given in Theorem 1 under given bound of Λkby applying the binary search technique [5].The detailed steps are shown in Algorithm 1.Thus,the disturbance robustness is measured by γminfor different energy-limited DoS attacks characterized by Θ.However,with unknown controller,Theorem 1 does not fit LMI-based conditions because the matrixFis coupled withY1andY2in (29).In the following,a controller solver is proposed based on the LMI technique,from which the coupled term vanishes.

B.Resilient H∞ Controller Design

Based on Theorem 1,we provide an algorithm to design controllerFfor system (11)with bounded transmission intervals.

Algorithm 1Linear search to calculation of the minimal γminwith given controller and bounded transmission interval.

Theorem 2:For some given scalars Λmin,Λmax,a,andb,the system (11)is asymptotically stable withH∞performance γ via controllerF=if there exists real matrices,K∈Rp×randY0∈Rr×r,such that,for Λk∈[Λmin,Λmax]

where

By setting Λmin=T0and Λmax=(Θ+1)T0,Theorem 2 is naturally extended to design LFC gain for (9)with a resilience of Θ and a disturbance attenuation level of γmin.The detailed procedure is introduced in the following subsection.

C.Procedure of Decentralized Resilient H∞ LFC

Based on the two theoretical results mentioned above,the decentralized resilientH∞LFC design scheme can be summarized by the following :

Step 1:Model construction and determining the parameters of the system model and the sampling periodT0of transmission signal.

Step 2:ResilientH∞LFC design.If Θ characterizing energy-limited DoS attacks is known,go to Step 2.1;IfH∞performance index γ is given,go to Step 2.2;If they are both given,go to Step 2.3.

Step 2.1:1)Initialize a search interval [γstart,γend] where γendis a large enough scalar and set an accuracy coefficient γac=0.001.2)Check whether (19)–(21)are feasible for system (9)with a testedH∞performance index γtest=(γend+γstart)/2.3)If (19)–(21)are feasible,set γend=γtest;else,set γstart=γtest.4)If |γend−γstart|<γac,obtain minimal γmin=γtestand compute controller byF=;else,go to 2).

Step 2.2:1)Initialize a search interval [Θmin,Θmax] where Θmin=0 and Θmaxis a large enough integer and set an accuracy coefficient Θac=0.001.2)Check whether (19)–(21)are feasible with a tested Θtest=(Θmax+Θmin)/2.3)If(19)–(21)are feasible,set Θmin=Θtest;else,set Θmax=Θtest;4)If |Θmax−Θmin|<Θac,obtain the maximum count of continuous data losses Θ=⎿Θtest」 and the controller computed byF=;else,go to 2).

Step 2.3:1)Given Θ and go to Step 2.1,obtain the minimal γ.2)If γ≤γgwhere γgis given,the pair [γg,Θ] is introduced to Theorem 2 by which the controller is computed byF=;else,the controller can not be found.

Step 3:Performance analysis and verification.One the one hand,utilize Theorem 1 to analyze theH∞performance index of controller under energy-limited DoS attacks,and find the relationship between γ and Θ.On the other hand,by simulation verification,the effectiveness of proposed LFC scheme is shown by comparing with the existing controller.

According to Step 2.1,the load frequency controller with energy-limited DoS attacks characterized by Θ is designed by minimizingH∞performance index γ.In Step 2.2,the load frequency controller with designatedH∞performance index is designed by maximizing the count of continuous data losses Θ induced by DoS attacks.If both Θ and γ are given,Step 2.3 provides a verification to determine whether the given pair[γ,Θ]satisfies the conditions for control design.If not,we need to make a trade-off between γ and Θ for achieving control objective.

Remark 5:The impact of the DoS attacks (or disturbance)could be alleviated by maximizing Θ (or minimizing γmin).By this proposed looped functional method,we use Theorem 2 and Step 2.2 (or Step 2.1)to find the maximum Θ (or minimum γmin)ensuring that the modeling LFC system is stable with given γmin(or Θ).A larger Θ means more resilience for controller against DoS attacks,and a smaller disturbance attenuation ability for controller against load disturbance.Note that PID-type controllers can be evaluated in this method,because it can be multiplied by the corresponding output matrix to convert into a state-feedback controller [21].This can provide comparisons among different controllers in the following numerical examples.

IV.CASE STUDY

The effectiveness of the proposed resilientH∞LFC scheme is verified in a one-area CPPS in Section IV-A,three-area CPPS with one generation unit in Section IV-B,and three-area CPPS with two generation units in Section IV-C.All computations and simulations were completed by MATLAB 2018b running on a PC with 1.8-GHz Intel Core i5 CPU,8GB RAM,Windows 10 64-bit Ultimate.

A.One-Area CPPS

In the one-area power system,the system is equipped with a generation unit.For the purpose of comparison,the model parameters of this one-area LFC system borrowed from [21] is shown in Table I.Preset sampling periodT0=2 s,H∞performance index γ=12,integral gainKI=1,controlled output wights λ1=1 and λ2=0.1,with turning parametersa=2 andb=0.Then,using Theorem 2 and Step 2.2 with a search interval [0,20],the maximum transmission interval (MATI)and the parameters of resilientH∞controller are shown in Table II.

TABLE I PARAMETERS OF ONE-AREA LFC SYSTEM

TABLE II THE MATIS FOR DIFFERENT CONTROLLERS

The performance of the proposed method is compared with that offourcontrollers employed from [10]–[12],[21],namedF1−F4.More specifically,F1works in sampled-data mode whileF2−F4work in continuous-time mode.F2uses a PID type controller while the others are all state feedback controllers.All parameters of the controllers are shown in Table II.

For each controllerF1−F4,compute its MATIs according to Corollary 1,and the results are shown in Table II.It is seen that the controllersF2−F4,working in continuous-time mode,can ensure the asymptotic stability of the one-area LFC system withw(t)=0 when the MATIs are smaller thanT0.Thus these controllers are ineffective for the secondary frequency control of this system.Although controllerF1can stabilize the system with the MATI 4.97s,it only tolerates the DoS attacks characterized by Θ=1.However,theFdesigned by the proposed method could tolerate those of Θ=3.This shows that the proposed looped functional methodV(t)is less conservative than that of [21],as analyzed in Remark 4.

In simulation,the load disturbance is introduced with a step change ∆Pd=0.1p.u.(t≥0)to quantify the performance of controllersFandF1under different DoS attacks.As shown in Fig.3(a),bothFandF1could stabilize the one-area LFC system under the step disturbance when the DoS attack satisfies Θ=1.When Θ=3,it is shown in Fig.3(b)thatFcan stabilize this system whileF1destabilizes the system.These verified thatFbehaves better thanF1in the aspect of resilience against DoS attacks.

Fig.3.Frequency deviation for one-area power system equipped with load frequency controllers F and F1 under different energy-limited DoS attacks.

In addition,setting theH∞performance level γ=12,the MATI of controllerF1computed by Theorem 1 is 3.916 s,which means thatF1cannot provide resilience against DoS attacks whenT0=2 s.

B.Three-Area CPPS With One Generation Unit

To further show the effectiveness of the proposed method,a three-area CPPS is considered to verify the robustness against the step change load disturbance and random load disturbance,and the resilience against the energy-limited DoS attacks.Suppose that each area equips with one equivalent generation unit as seen in Fig.4.The dynamic model of each area follows the control structure in Fig.1.The detailed parameters of each area referring to [33] are shown in Table III.The sampling period of the transmission signals is set to beT0=3 s.

The Design of the Controller:Based on Theorem 2 and Step 2.1 with Λmin=3,Λmax=12,λ1,i=1,λ2,i=0.1,KI,i=2(i=1,2,3),a=0.49,b=0,γstart=0,and γend=20,the resilientH∞controllers for the tested three-area CPPS are respectively designed as

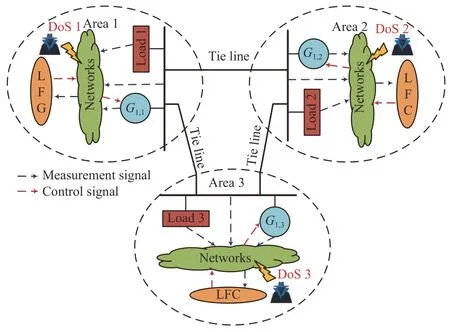
Fig.4.Topology of 3-area power systems.

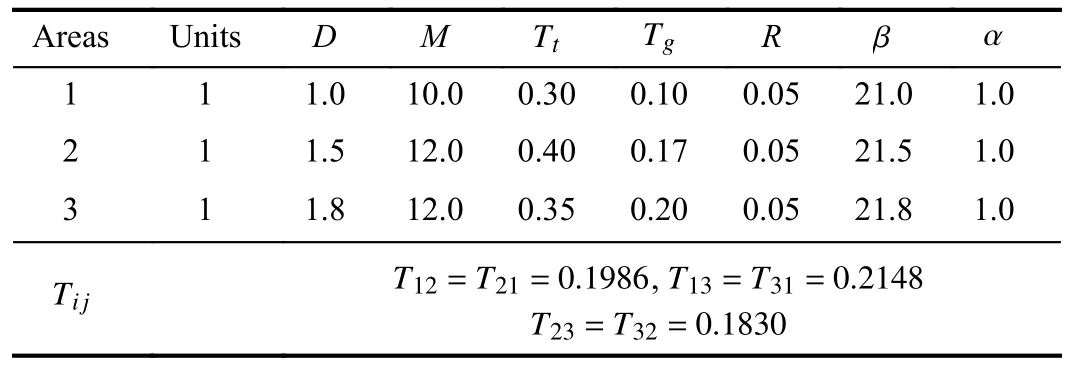
TABLE III PARAMETERS OF THREE-AREA LFC SYSTEM

The Analysis of theH∞Performance:We substitute respectively the obtained controllersFA1,FA2,andFA3to Theorem 1 under Λmin=T0and Λmax=(Θ+1)T0with different values of Θ.By Algorithm 1,the computation results on theH∞performance index γminare listed in Table IV.In order to facilitate the observation,these results are presented in Fig.5 in a bar chart form,concluding that the designed controllersFA1−FA3for each area can guarantee that theH∞performance index γminonly increases in a small range when DoS-induced Θ varies from 0 to 3.This shows that the proposed LFC scheme is resilient to the energy-limited DoS attacks while guaranteeingH∞performance.

TABLE IV THE H∞ PERFORMANCE INDEX γmin FOR EACH AREA UNDER DIFFERENT DOS-INDUCED Θ

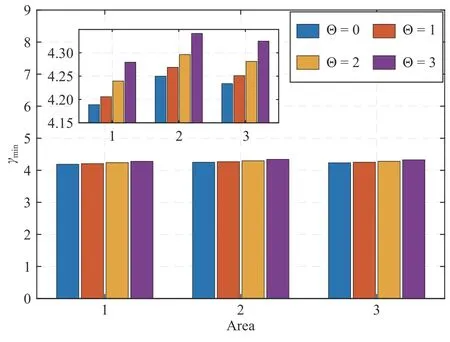
Fig.5.The minimal γmin for different DoS-induced Θ with FA1,FA2,and FA3.

On the other hand,the integration of ACE in (3),in which the integration gainKI,iis given for each area in this paper,is introduced to design the resilient LFC scheme.Actually,the parameter selection of the integration gainKI,ifor each area can affect theH∞performance of the designed controller.Under the parameters Λmin=3,Λmax=12,λ1,i=1,λ2,i=0.1,a=0.49,b=0,γstart=0,and γend=10,we compute theH∞performance index γminfor controllerFA2of area 2 under different parameters ofKI,2based on Theorem 1 and Algorithm 1.These results are listed in Table V.Resultsof areas 1 and 3 are similar and are omitted here.From these results,the values of γminfirst decrease and then increase with respect toKI,2.The reason follows that a small integration gainKI,2can effectively eliminate the frequency derivation in the ACE-based LFC implementation to improveH∞performance.But the larger integration gainKI,2can accumulate the larger error of the system to degrade theH∞performance.Thus,it can provide a guide for us to choose a suitableKI,ifor each area under given controller gains and energy-limited DoS attacks.As ongoing research,we will make efforts to develop a way to obtain an optimal selection ofKI,iunder constraints.

TABLE V THE H∞ PERFORMANCE INDEX γmin FOR AREA 2 UNDER DIFFERENT KI,2

Simulation Verification:In order to show the necessity of considering both sampling periods,which is generally set in the range of 2 s−4 s in the operation of real power system,and the effect of DoS attacks,we compare the proposed scheme with the other two LFC schemes against DoS attacks as follows:1)The switching system-based decentralized PItype LFC scheme considering both DoS duration and frequency is proposed in [32],and under the same sampling period 3 s asT0,the proposed controller is named asC1which consists ofC11=[−0.0741−0.1379],C21=[−0.0893−0.1623]andC31=[−0.0741−0.1379] for each area; 2)The centralized resilient PI-type LFC scheme [6] based on a QoSdependent event-triggered communication strategy is proposed in [6],and under an updating period smaller than 1 s,the proposed controller is named asC2which consists ofC12=[−0.0164−0.3674],C22=[−0.0306−0.3330] andC32=[−0.0264−0.3475]for each area.

To verify the effectiveness of the proposed LFC scheme,the system equipped with the above three controllers is tested in two kinds of load disturbances:the step change and random load disturbances.Assume that the increments of step change load disturbances of three areas are ∆Pd,1=0.07 p.u.,∆Pd,2=0.08 p.u.and ∆Pd,3=0.05 p.u.fort≥0,respectively.The random load disturbances of three areas are depicted in Fig.6.Since the designed controllersFA1−FA3is based on Λmax=4T0,the maximum count of continuous data losses Θ induced by DoS attacks for each communication channel is set as 3 according to (7).Then,Figs.7–9 give the response of frequency deviation for each area under two different load disturbances and DoS 1–3 satisfying this Θ=3 of limitation,respectively,in which“DoS 1(2,3)=1”means having DoS attacks and“=0”otherwise.

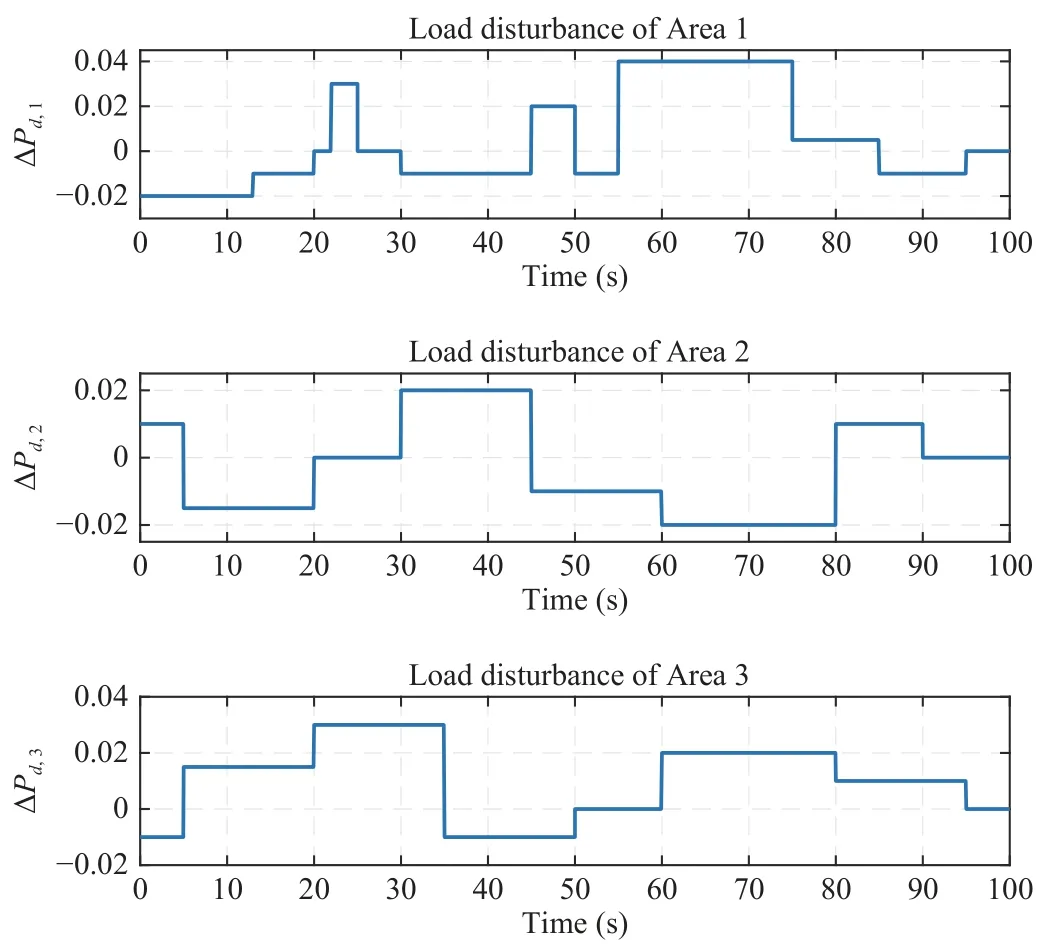
Fig.6.Random load disturbances of three areas.

Fig.7.The response of frequency deviation of area 1 under FA1,C11,and C12.

Fig.8.The response of frequency deviation of area 2 under FA2,C21,and C22.

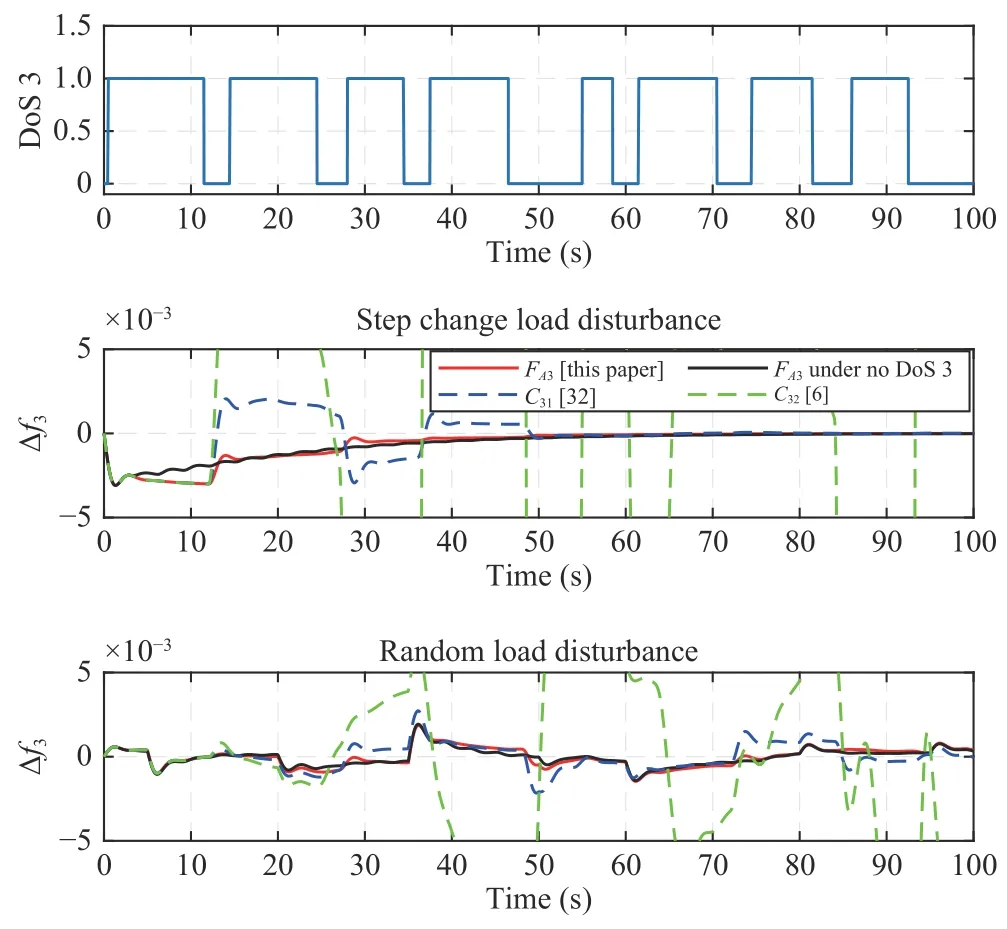
Fig.9.The response of frequency deviation of area 3 under FA3,C31,and C32.

From Figs.7–9,it is seen that under the given sampling periodT0,the state-feedback controllersFA1−FA3designed by the proposed method can ensure the frequency stability in the presence of DoS attacks characterized by Θ=3.In the absence of DoS attacks,the control performance ofFA1−FA3are slightly better than those in the presence of DoS attacks.This shows that the designed controllers can ensure the certain control performance changeless regardless of whether there is an attack happening,and it means that the proposed LFC scheme is resilient to DoS attacks.However,the control performance ofC1is degraded in comparison to the proposed one,and even controllerC2is incapable of stabilizing the system.There are two reasons for this :

1)The controllerC1reported in [32] is designed under the same sampling period asT0based on the model of switching system,including the DoS-induced unstable subsystem and the stable subsystem without DoS happening,which is obtained by discretizing the original continuous LFC system by treating the sampling period as the discrete step.When the sampling period is selected in the range of 2 s–4 s in the real LFC process,the discrete model may be unable to restore the dynamics of the original system due to distortion.However,controllersFA1−FA3are designed based on the model of aperiodic sampled-data system,which holds the continuity of original LFC system by a looped functional method.

2)The controllerC2reported in [6] is designed under the allowable maximum updating period 1s while implementing a QoS dependent event-triggered communication strategy.However,it is less thanT0,and thus the controllerC2is infeasible against DoS attacks in the real LFC process.

Consequently,the state-feedback controllersFA1–FA3designed by the proposed resilientH∞LFC scheme are effectively implemented to regulate the frequency of this studied CPPS with guaranteedH∞performance and resilience in the presence of load disturbances and DoS attacks.

C.Three-Area CPPS With Two Generation Units

Suppose that in a three-area LFC system,where each area is equipped with two generation units,has a topology found in Fig.4.The dynamic model of each area follows the control structure in Fig.1.The detailed parameters of each area,as found in [37],are shown as Table VI.The sampling period of transmission signals is set to beT0=2 s.

TABLE VI PARAMETERS OF THREE-AREA LFC SYSTEM

The Design of the Controller:Based on Theorem 2 and Step 2.1 with Λmin=2,Λmax=14,λ1,i=1,λ2,i=0.1,KI,i=1(i=1,2,3),γstart=0 and γend=20,the resilientH∞LFC controllers for three areas are respectively designed as

The Analysis of theH∞Performance:We substitute respectively the controllersFA1,FA2,andFA3to Theorem 1 under Λmin=T0and Λmax=(Θ+1)T0with different values of Θ.Based on Algorithm 1,the computation results onH∞performance index γminare depicted as Fig.10.It shows that for each area,a larger Θ leads to a lager γmin,which implies the bad effects of DoS attacks on the disturbance attenuation ability of controllers.However,the increment of γminfrom Θ=0 to Θ=8 is smaller than 0.02,which means that the designed controllers are resilient to DoS attacks while guaranteeingH∞performance.

Fig.10.The minimal γmin for different DoS-induced Θ with FA1,FA2,and FA3.

Simulation Verification:For comparisons,the continuoustime decentralized PI-type controllers,i.e.,area 1:PI 1=[−3.27e−04−0.3334],area 2:PI 2= [−6.96e−04−0.3435],and area 3:PID 3= [−1.60e−04−0.3398],reported in [37],is utilized to compare withFA1,FA2,andFA3obtained by our proposed method.Consider two kinds of load disturbances,i.e.,the step change and random pulse load disturbances.Assume that the increments of step change load disturbance of three areas are ∆Pd,1=−0.1 p.u.,∆Pd,2=0.08 p.u.,and∆Pd,3=0.05 p.u.fort≥0,respectively.The random pulse disturbances are depicted in Fig.11.The maximum count of continuous data losses Θ induced by DoS attacks for each communication channel is set as 6.Then,Figs.12–14 give the response of frequency deviation of each area under the above two classes of load disturbances.

Figs.12–14 show that the state-feedback controllers designed by the proposed scheme effectively stabilize the LFC system resilient to DoS attacks characterized by Θ=6,while the PI-type controllers reported in [37] are not resilient to such DoS attacks.There are two reasons for this:

1)The PI-type controllers reported in [37] are designed based on genetic algorithms and linear matrix inequalities without considering the sampling period and the effect of DoS attacks.

Fig.11.Random pulse load disturbance.

Fig.12.The response of frequency deviation of area 1 under FA1,C11,and PI1.

2)It is found from the Table I of [37] that the minimal γminof the controllers PIs 1–3 are larger than the designed controllers as seen in Fig.10.This shows that the proposed controllers are more resilient to DoS attacks than that of [37]with betterH∞performance.

Consequently,the proposed resilientH∞LFC scheme is also effective to ensure the stability of frequency for the three-area CPPS with two generation units.

Fig.13.The response of frequency deviation of area 2 under FA2,C21,and PI2.

Fig.14.The response of frequency deviation of area 3 under FA3,C31,and PI3.

Remark 6:Different from continuous-time output-based LFC design in [5],the proposed sampled-data state-feedback LFC design does not involve the optimization solution for nonlinear LMIs,which further reduces complexity.In some works,e.g.,[38],the power system suffered from DoS attacks is modeled as a time-varying delay system,while the sample limitation is not be considered.Moreover,how to reveal the active action of attackers and passive influences of networkinduced communication delay should be further studied.Of course,it is undeniable that the PID control is commonly used in practice due to the lower cost for sensor deployments and excellent performance,which also encourage us to further investigate PID-based LFC scheme against DoS attacks.

V.CONCLUSION

A decentralized resilientH∞LFC scheme for a multi-area CPPS under DoS attacks was investigated in this paper.By limiting the DoS attacks with a characterization of the maximum count of continuous data losses implying the resilience index,we developed a model of aperiodic sampleddata control system against the closed-loop LFC system.Additionally,we developed the BRL of the LFC scheme under DoS attacks based on the proposed transmissioninterval dependent looped functional method.Then,the statefeedback controller gains of the LFC scheme could be determined with guaranteedH∞performance and resilience index based this BRL.When the controller gains were given,the LFC scheme could test for theH∞performance and resilience index.Simulation tests have been undertaken on the one-area CPPS and two three-area CPPSs.The simulation results have shown that the LFC scheme with the designed state-feedback controller can tolerate DoS attacks with resilience index while ensuring the guaranteedH∞performance.

In the future,by combining with the proposed method,the time-varying transmission delays and event-triggered sampling scheme will be considered as ongoing research directions for LFC schemes under DoS attacks.

APPENDIX A USEFUL LEMMAS

Lemma 1 [39]:Let Υ0,Υ1,and Υ2be compatible real symmetric matrices and a continuous function τ satisfy τ1≤τ≤τ2,where τ1and τ2are constants satisfying 0≤τ1≤τ2,if Υ0≥0,then the following inequalities are equivalent:

APPENDIX B PROOF OF THEOREM 1

For the sake of simplification,the following nomenclatures are used:

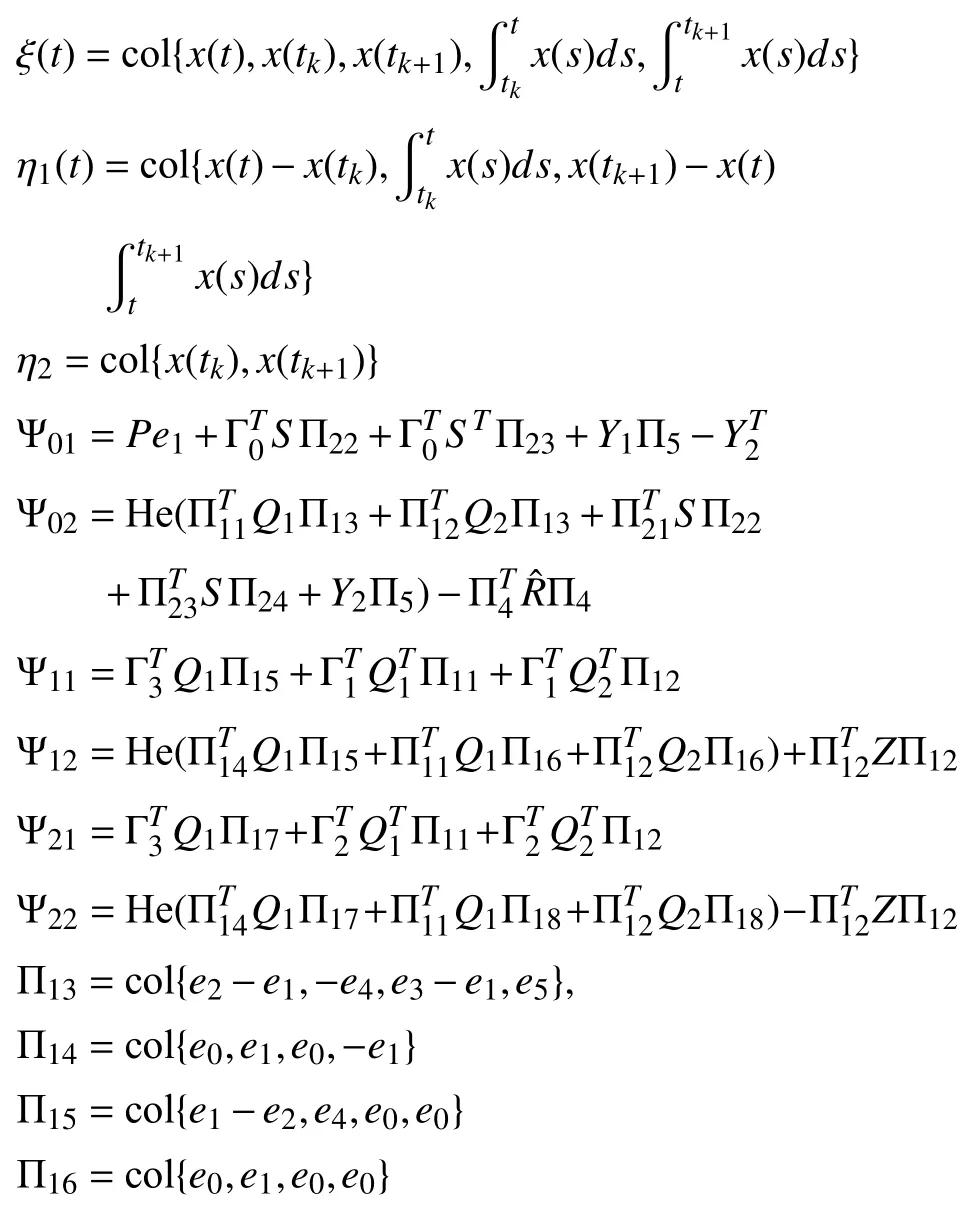
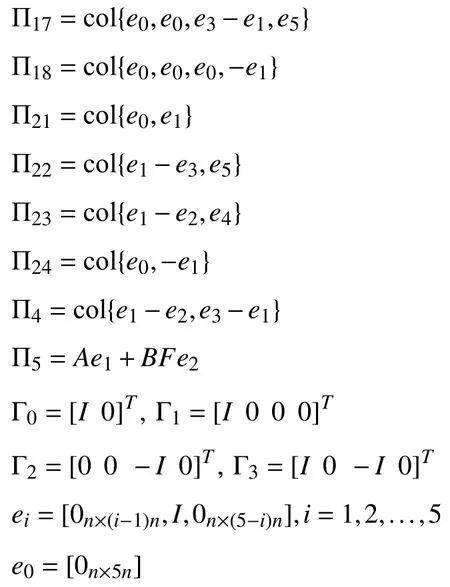
whereP,Ql,S,Z,andYl(l=1,2)are denoted in Theorem 1.

Proof:Consider the following transmission intervaldependent looped functional candidate:

where

withRlfori=1,2,Z=ZT,andQ,Sgiven in Theorem 1.

It is seen thatV(t)=xT(t)Px(t)at sampling instantst=tk,k=1,2,...,thus this is a looped functional according to[18].Since the objective here is to guarantee that the variation ofV(t)between two successive sampling instants is strictly negative by Theorem 1 of [17],the remainder of this proof ensures that fort∈(tk,tk+1),<0 holds.In the following,take the time derivative ofV(t)along system (11)yields:

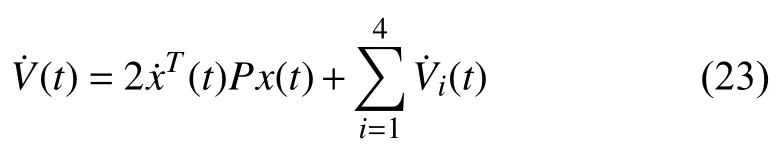
where

Using Jensen inequality and reciprocally convex combination inequality to deal with integral terms mentioned above,then they are estimated as

where Π4is denoted in Theorem 1 andfor any compatible real matrixX.

From (23)and (24),after some simple algebraic manipulations,one is rewritten as

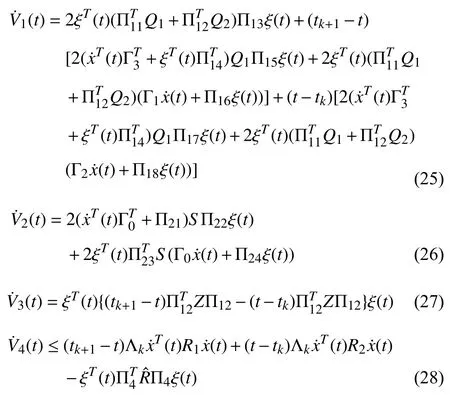
where the notationseand Π with different subscripts are given in Theorem 1.

On the other hand,the free matrixY1andY2are introduced by the following zero equations:

where Π5is given in Theorem 1.

Based on (25)–(29),after rearrangement we have

where Ψi1and Ψi2(i=0,1,2)are denoted in Theorem 1.

Consequently,it is seen that if the inequalities hold

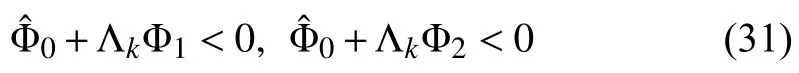
which are equivalent to (13)and (14)such thatV˙(t)+zT(t)z(t)−γ2wT(t)w(t)<0.Then,it follows from (13)and (14)that for givenk≫1,we integrate (30)from 0 tilltksuch that:

Since the loop conditionsV(t)=xT(t)Px(t),t=tk,k=1,2,...,andV(tk)≥0 with zero initial conditionV(0)=0,we have.According to the conclusion of Theorem 1 of [17],the system (11)is asymptotically stable withH∞performance index γ. ■

APPENDIX C PROOF OF THEOREM 2

Proof:This line of proof is similar to [31].If LMIs (13)is feasible,,which means thatY1is invertible.Thus,the following transformation matrix is introduced as:

Notice that,

SetY2=where Π0=ae1+be2,andaandbare two turning parameters.Then,multiplying (13)by the left and right by J and its transpose,the following variables are replaced as:

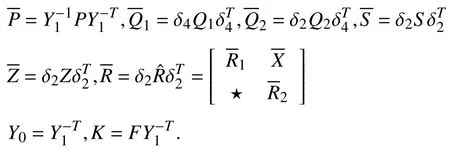
Performing the same transformation to (14),it is easy to obtain (19)and (20).Thus,if (19)–(21)hold,then (13)–(15)hold.According to Theorem 1,the system (11)satisfiesH∞stability under controllerF=. ■