Data-Driven Heuristic Assisted Memetic Algorithm for Efficient Inter-Satellite Link Scheduling in the BeiDou Navigation Satellite System

Yonghao Du,Ling Wang,Lining Xing,Jungang Yan,and Mengsi Cai

Abstract—Inter-satellite link (ISL)scheduling is required by the BeiDou Navigation Satellite System (BDS)to guarantee the system ranging and communication performance.In the BDS,a great number of ISL scheduling instances must be addressed every day,which will certainly spend a lot of time via normal metaheuristics and hardly meet the quick-response requirements that often occur in real-world applications.To address the dual requirements of normal and quick-response ISL schedulings,a data-driven heuristic assisted memetic algorithm (DHMA)is proposed in this paper,which includes a high-performance memetic algorithm (MA)and a data-driven heuristic.In normal situations,the high-performance MA that hybridizes parallelism,competition,and evolution strategies is performed for highquality ISL scheduling solutions over time.When in quickresponse situations,the data-driven heuristic is performed to quickly schedule high-probability ISLs according to a prediction model,which is trained from the high-quality MA solutions.The main idea of the DHMA is to address normal and quick-response schedulings separately,while high-quality normal scheduling data are trained for quick-response use.In addition,this paper also presents an easy-to-understand ISL scheduling model and its NPcompleteness.A seven-day experimental study with 10 080 oneminute ISL scheduling instances shows the efficient performance of the DHMA in addressing the ISL scheduling in normal (in 84 hours)and quick-response (in 0.62 hour)situations,which can well meet the dual scheduling requirements in real-world BDS applications.

I.INTRODUCTION

ON June 23,2020,the 55th satellite in the BeiDou Navigation Satellite System (BDS)was launched into orbit,completing the deployment of the new-generation global navigation satellite system around the earth [1].Over the years,the BDS has been providing full-time navigation and position services across the world and playing an increasingly important role in terms of logistics,transportations,aeronautics,and astronautics.To obtain high performance in navigation and position services,inter-satellite ranging and communication are always needed since some BDS satellites cannot be full-time visible to ground facilities.Under such circumstances,the inter-satellite links (ISLs)that support ranging and communication among satellites turn into important components of the BDS [2].

The ISL is a wireless link between two satellites,which can transfer data and perform ranging in space.With the ISLs,satellites can be linked and thereby controlled even if they are not visible to ground facilities.The ISLs were first equipped on GPS Block IIR satellites [3] and are currently used in the BDS [4],[5],and Galileo [6].However,due to the limited ISL antennas equipped on satellites,only a few of ISLs can be activated simultaneously.Therefore,to guarantee full-time ranging and communication in the BDS,the scheduling of ISLs among satellites is full-time needed over time.In other words,the BDS must frequently schedule its ISLs among satellites,contributing to a time-varying satellite inter-linking network for higher system performance.

In general,the ISL scheduling is the process of determining which ISLs should be activated among satellites at every moment.With the current applications of narrow-beam antennas that outperform in speed,flexibility,accuracy,and anti-jamming capability,the BDS management agency prefers dividing the timeline into superframes (instances,often in minutes),and further dividing each superframe into timeslots(often in 3 seconds).Hereby,the ISL scheduling is performed per superframe to activate proper ISLs within each predivided timeslot,as shown in Fig.1.During a superframe,some of the satellites are tracked by ground facilities,also called anchor satellites that can downlink other satellite data transferred by ISLs before.Given that information,the ISL scheduling optimizes a certain objective,such as the average satellite data delay in the BDS during a superframe,subject to some required constraints considering satellite visibility and antennas.

Although efforts have been made to model and solve the ISL scheduling,it has received much less attention than other types of satellite scheduling such as satellite imaging scheduling and range scheduling [7]–[9].To address the seven-day ISL scheduling including 10 080 superframes in the 30-satellite BDS,Yanget al.[10] designed a discrete differential evolution (DDE)algorithm and reduced over 70%of satellite data delays to 1 timeslot (as many as 3 seconds),supporting at least 9 different inter-satellite rangings per satellite in a one-minute superframe.Similarly,Sunet al.[4]designed a phased scheduling framework with a genetic algorithm to reduce the average delay to 2.12 timeslots (as many as 6.16 seconds)and obtained satisfying position dilution of precision.Assuming future ISLs would hybridize lasers and radios,Liuet al.[11] optimized via simulated annealing (SA)and showed that the SA was much more efficient than the DDE.In addition,other rule-based heuristics and metaheuristics such as fireworks algorithm and greedy randomized search were also developed in related studies[12]–[16].

However,previous studies often addressed the ISL scheduling in normal situations,such as the seven-day scheduling mentioned above,and the computing time via metaheuristics was seldom discussed.On the one hand,even if a one-minute superframe takes only 1 second for ISL scheduling,the seven-day scheduling including 10 080 superframes would last 2.8 hours,which was still an unacceptably time-consuming process.On the other hand,since the ISL scheduling depends on the facts about anchor satellites,re-scheduling is urgently required once the anchor satellites are changed with higher priorities.In fact,this phenomenon often occurs due to many dynamic and uncertain factors in the BDS daily management and troubles the management agency a lot.Therefore,previous ISL scheduling studies could hardly meet the quick-response scheduling requirements that often occur and lack computing time,and a new algorithm that is qualified for ISL scheduling inboth quick-response and normal situationsis truly needed.

To address the quick-response scheduling,the data-driven and machine learning algorithms that have been studied in other satellite scheduling problems show great competitiveness.For example,in the case of imaging satellite scheduling,Liuet al.[17] and Xinget al.[18] extracted task features from history daily data and adopted BP neural networks to predict the probabilities that tasks can be successfully scheduled.Duet al.[19] designed a data-driven parallel scheduling framework where daily data were trained via neuro-evolution so as to perform prediction,task assignment,and scheduling acceleration.Considering satellite range and downlink scheduling,Songet al.[20] also suggested using daily data and further designed a general-use data-driven scheduling framework including over 6 types of machine learning algorithms.When it comes to the studied ISL scheduling in the BDS,it has a particular advantage required in data-driven applications,namely,it can provide a considerable number of data every day.Specifically,over seven-day management,10 080 and only 7 instances of daily data can be collected in normal ISL scheduling and imaging satellite schedulings,respectively.Therefore,compared with other satellite scheduling,the ISL scheduling here is much more appropriate for data-driven applications in quick-response situations,as shown in Fig.2,where a large number of daily data can offer great potential.

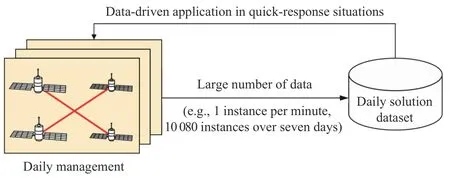
Fig.2.A large number of ISL scheduling daily data can offer great potential.

To obtain high-quality solutions for normal ISL scheduling,as well as high-quality data for the data-driven quick-response scheduling mentioned above,a high-performance metaheuristic algorithm is also needed.In combinational optimization studies,it is acknowledged that local search and evolutionary algorithms (EAs)outperform in exploitation and exploration,respectively,and the memetic algorithms (MAs)that hybridize these two algorithms often show good overall performance.The MAs have been applied to many satellite scheduling and other challenging problems [21]–[25],but the hybridization also results in the superposition of computing time taken by those two algorithms.From another point of view,recent developments of computer hardware have motivated a great many algorithmic studies in a parallel and competitive manner,where computing resources can be fully used [26]–[30].Certainly,it is uneconomic to use those algorithms that leave many computer threads unused in realworld applications.Moreover,given the same computing time,the parallel threads that run different algorithms or operators can produce much more diversified results,which also satisfy the required diversity by EAs or MAs.Therefore,the parallelism and competition are proper additional strategies that can accelerate and strengthen a MA and make it appropriate for the ISL scheduling in this paper.

With those motivations,a data-driven heuristic assisted memetic algorithm (DHMA)is proposed in this paper to address the dual requirements of normal and quick-response ISL schedulings.In this algorithm,1)in normal situations,a high-performance MA that hybridizes parallelism,competition,and evolution strategies is designed to obtain highquality ISL scheduling solutions,while 2)in quick-response situations,a data-driven heuristic is designed to quickly schedule high-probability ISLs according to a prediction model,which is trained from the high-quality MA solutions.The main idea of the DHMA is to address normal and quickresponse schedulings separately,while high-quality normal scheduling data are also trained for quick-response use.A seven-day experimental study in this paper will show the DHMA performance in real-world BDS applications.

The contribution of this paper includes 1)the efficient algorithm called DHMA that properly addresses the dual requirements of normal and quick-response ISL schedulings in the BDS,and 2)an easy-to-understand model that clearly describes the ISL scheduling problem.

The remainder of the paper is organized as follows:In Section II,an easy-to-understand model and complexity analysis of the ISL scheduling are given.In Section III,the framework of the DHMA along with its inner highperformance MA and data-driven heuristic is designed.Then,the DHMA is examined in a seven-day ISL scheduling experiment in Section IV.Finally,the paper ends with the discussions and conclusions in Sections V and VI,respectively.

II.ISL SCHEDULING MODEL

In this section,the ISL scheduling is illustrated and explained with a four-satellite example for easy understanding.Then,the mathematical formulations including variables,constraints,and the objective are presented to build the full ISL scheduling model.Also,the model complexity and its NP-completeness are given.

A.Preliminaries

Before modeling the ISL scheduling in this section,some preliminaries and reasonable assumptions should be given first.The preliminaries include:

1)In the BDS,satellites can be divided into anchor satellites and non-anchor satellites,which are currently tracked and untracked by ground facilities,respectively.

2)Satellites produce data at every moment.The data from anchor satellite can be real-time downlinked,but those from non-anchor satellites must be transferred to anchor satellites via ISLs and then downlinked;hence,the data transferring determines the data delay.

3)The BDS management agency prefers dividing the timeline into superframes (instances,often in minutes),and further dividing each superframe into timeslots (often in 3 seconds).Thereby,the data delay can be counted in timeslots,namely,how many timeslots will be taken by data transferring.For example,given an ISL that links an anchor satellite and a non-anchor satellite,their current data delays will be 0 and 1 timeslot,respectively.

Also,some reasonable assumptions are needed to support those preliminaries and build a proper model for the ISL scheduling studied in this paper:

1)Given all the inputs of an ISL scheduling superframe,dynamic or uncertain factors no more occur and will not be considered in this scheduling process.

2)Each satellite is equipped with only one ISL antenna,and the antenna can only support one ISL per timeslot.

3)Within a timeslot,if a satellite is not linked by any ISL,the data will be stored onboard.Alternatively,it can be considered that there is a self-ISL that links this satellite.

4)During data transferring among satellites via ISLs,the data will be completely transferred without any failure or loss.

B.Model Explanation

To explain the ISL scheduling model in an easy-tounderstand manner,a four-satellite ISL scheduling instance example is illustrated to show how the ISLs construct a timevarying satellite inter-linking network.

Assuming that there are four satellites in the BDS,and i)In timeslot 1,an ISL links satellites 1 and 2,and another one links satellites 3 and 4;ii)In timeslot 2,an ISL links satellites 1 and 3,and another one links satellites 2 and 4;iii)In timeslot 3,an ISL links satellites 1 and 4,and another one links satellites 2 and 3.Two different views of the ISLs within these three timeslots are shown in Fig.3,where Fig.3(b)intuitively shows how the satellites are inter-linked per timeslot.

Fig.3.Different views of four-satellite ISLs within three timeslots.(a)Inter-satellite links across timeslots.(b)Inter-satellite links per timeslot.

To properly understand the time-varying satellite interlinking network constructed via ISLs,Fig.3(a)is explained here.In Fig.3(a),an ISL links two satellites across the timeslot,namely,links the satellites at two different moments.In this view,the data of satellite 1 (marked in red)within timeslot 1 will be transferred through the red lines to satellites 2,4,and 1,within timeslots 1,2,and 3,respectively.Hereby,if satellite 4 is an anchor satellite,the data delay will be 2 timeslots (including timeslots 1 and 2)since the data can be downlinked by satellite 4 within timeslot 3,no longer transferred to satellite 1.Therefore,the ISLs that link satellites across timeslots can be viewed as the routes of data transferring,so the data delay of any satellite within any timeslot can be counted.In addition,it can also be observed that those routes will never branch,since a satellite can only support one ISL per timeslot as the assumptions state.

In this regard,the ISL scheduling studied in this paper is explained for easy understanding.Then,it will be mathematically modeled in the next subsection,where the variables,constraints,and the objective of a scheduling problem will be formulated.

C.Mathematical Modeling

1)Variables

Following are the variables and their denotations that will be used in this paper:

S:the set of satellites in the BDS.

si:theith satellite in the BDS,si∈S.

T:the set of timeslots in the superframe.

ti:theith timeslot in the superframe,ti∈T.

lijk:the ISL between satellitessjandskwithin timeslotti.

vijk:a binary variable that indicates satellitesjis visible toskwithin timeslottior not by 1 or 0,respectively.

aij:a binary variable that indicates satellitesjis an anchor satellite within time timeslottior not by 1 or 0,respectively.

xijk:the binarydecision variablethat determines ISLlijkis activated between satellitessjandskwithin timeslottior not by 1 or 0,respectively.

dij:the dependent variable that indicates the delay of satellitesjwithin timeslotti(counted in timeslots).

2)Constraints

With the explanations and variables above,the constraints of the ISL scheduling studied in this paper are formulated as follows:

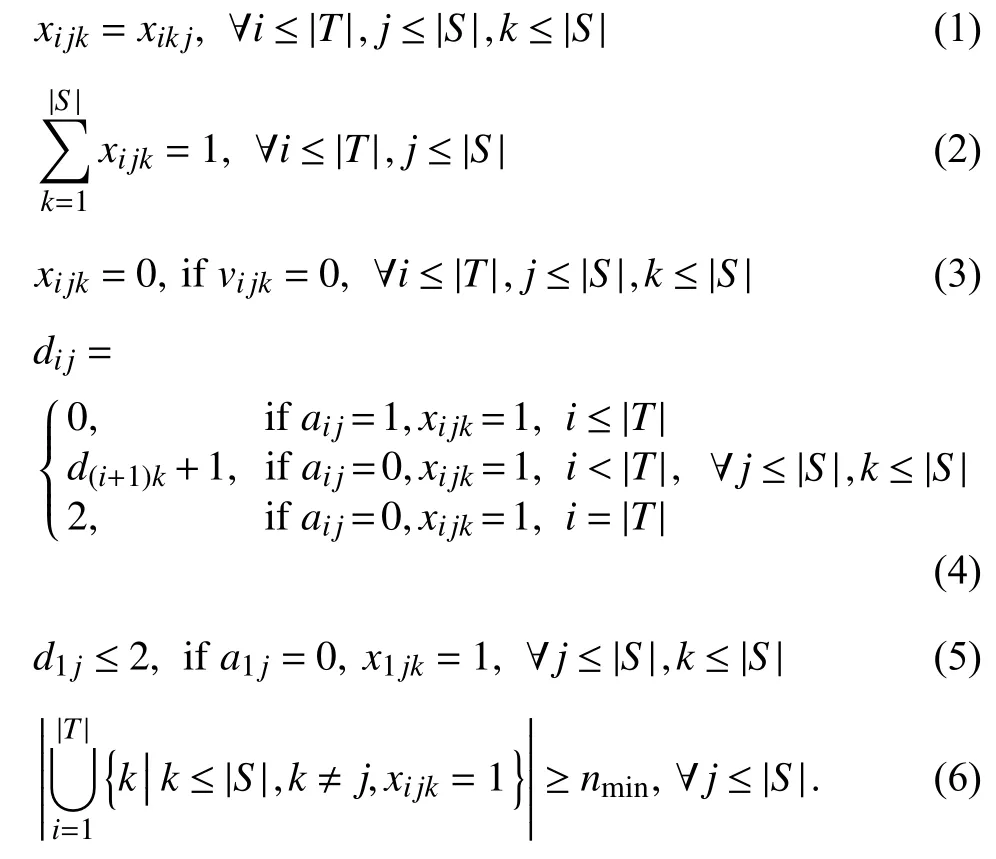
Constraint (1)indicates that the ISL is bi-directional,namely,ISLslijkandlikjare the same between satellitessjandsk.

Constraint (2)indicates that a satellite must and can only activate one ISL per timeslot,since there is only one ISL antenna equipped per satellite.In other words,regarding satellitesjwithin timeslotti,the ISLs that link satellitesjconflict with each other,and only one (lijk)of them is allowed.Herein,a self-ISL from satellitesj(xijj=1)is also allowed,which implies that no ISL is activated from satellitesjin fact.

Constraint (3)indicates that ISLlijkbetween satellitessjandskcan only be activated when these two satellites are visible to each other.

Constraint (4)counts delaydij(in timeslots)of satellitesjwithin timeslottiunder different conditions.i)Whensjis an anchor satellite (aij=1),delaydijequals 0 since the data can be real-time downlinked.ii)Otherwise (aij=0),when satellitessjandskare inter-linked (xijk=1),current delaydij(of satellitesjwithin timeslotti)equals next delayd(i+1)k(of satelliteskwithin timeslotti+1)plus 1,since current data of satellitesjwill be transferred to satellitesknext.iii)When it comes to the delay within the last timeslot (i=|T|),it is set to 2 here.

Admittedly,the delay within the last timeslot in (4)should have been calculated beyond this superframe,but the ISL scheduling is often performed given the pre-divided superframe [4],[10],[11].Hereby,to properly connect two continuous superframes,a compromising way is given in (5).That is,to ensure that the delay within the first timeslot (d1j)is no more than 2,so the ISL scheduling results of two continuous superframes can match up.

Finally,(6)counts the number of different ISLs activated by satellitesjin the superframe and makes it overnmin.Here,records the IDs of other satellites that inter-link satellitesjwithin all timeslots (except self-linkingj≠k).In other words,this constraint requires each satellite to support at leastnmindifferent inter-satellite rangings in the BDS in this superframe.

3)Objective

Different objectives were optimized in previous studies,where the average data delay in the BDS was the most commonly used [4],[10],[11] and concerned by the BDS management agency.Therefore,minimizing the average delay of non-anchor satellites in a superframe is set to the objective in this paper,as shown in

Although the multi-objective optimization that obtains Pareto solutions is a way that can consider other objectives,it is not adopted here,due to the following two reasons.On the one hand,only one solution (ISL schedule)will be finally performed on the BDS,and this paper is just motivated for this schedule.On the other hand,the multi-objective optimization that often uses EAs may take longer computing time for Pareto solutions,which can hardly fit the quickresponse ISL scheduling stressed in this paper.

Instead,to consider another often-mentioned objective,a compromising way that introduces a second-priority objective is adopted here.As shown in (8),a variant of (6)that maximizes the average number of different activated ISLs per satellite is set to the second-priority objective.Specifically,the ISL scheduling here always accepts a solution that outperforms in (7);if two solutions are the same in (7),the outperforming one in (8)will be accepted.

4)Complexity Analysis

This subsection gives some complexity analysis of the ISL scheduling problem modeled above.Given satellite setS,it can be easily derived that there aredifferent ISLs (except self-ISLs)that satisfy (1);then given timeslot setT,there will beISLs.Hereby,the binary decision variable in Section II-C will result incombinations.Therefore,the complexity of the ISL scheduling here is at leastO(2n),which is exponential.

To obtain delaydijof satellitesjwith timeslotti,(4)will calculate at most |T|-itimes.To obtain all delays in the ISL scheduling,(4)will calculate at most |S|×times,which is polynomial.The polynomial complexities can also be observed in other constraints.Therefore,the complexity that only evaluates the ISL scheduling is polynomial,so the ISL scheduling is a non-deterministic polynomial (NP)problem.

There would be many ways to show the NP-completeness of the ISL scheduling,and only an easy-to-understand one is given here,with the main idea that an NP-complete problem reduces to the ISL scheduling.

Proof:First,consider a subset (special case)in the ISL scheduling,that is,the one-timeslot scheduling,and only the constraints about bi-directional inter-linking,antennas,and delay are considered,via (1),(2),and (4),respectively.Given the satellite delays within the next timeslot by (4),the objective in (7)is to minimize the average satellite delay,namely,the total delays currently.

Then,describe this ISL scheduling subset as a minimization knapsack problem with conflict graphs (MKPC)[31].As shown in Fig.4,the timeslot and ISLs can be viewed as the knapsack and items in the MKPC,respectively,and the constraints in (2)can be viewed as the conflicts among the items.Also,(2)requires the minimum ISL number (when no self-ISLs),matching the minimum item number/weight required in the MKPC.For each ISL,it produces the delays of two satellites by (4),which can be viewed as the item value in the MKPC.Therefore,the ISL scheduling that minimizes satellite delays can be viewed as the MKPC that minimizes the item values,in conflict-free combinations.

Since the MKPC has been proven NP-complete [31],the ISL scheduling that includes the aforementioned subset is NPhard.Note that the ISL scheduling is also NP,thus it is NPcomplete. ■

Above all,this section well explains and models the ISL scheduling problem studied in this paper.Also,the complexity and NP-completeness of this problem are given.To address the dual requirements of normal and quick-response ISL schedulings stressed in this study,next section will design a data-driven heuristic assisted memetic algorithm,where a large number of ISL scheduling daily data will offer great potential.

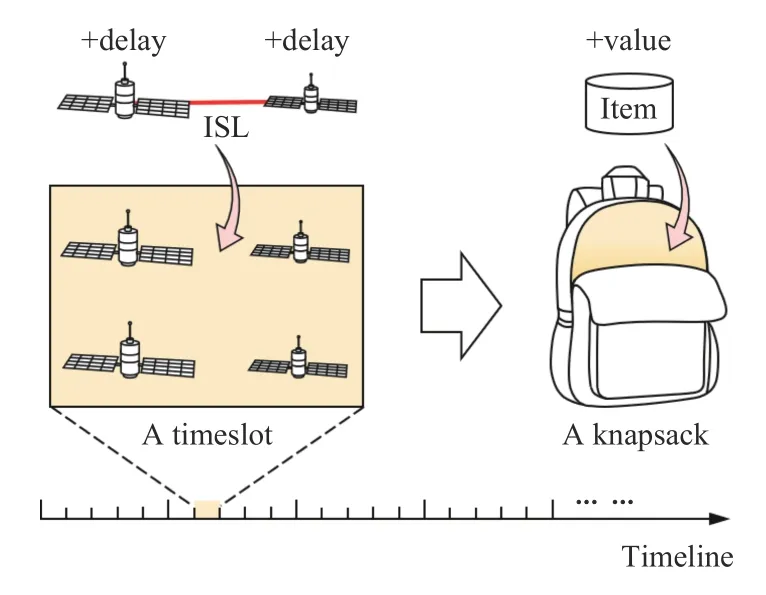
Fig.4.Viewing the timeslot and ISL as the knapsack and item,respectively.

III.DATA-DRIvEN HEURISTIC ASSISTED MEMETIC ALGORITHM (DHMA)

In real-world applications,the computing times allowed in normal and quick-response scheduling situations are certainly different.Metaheuristics often show good performance given certain computing time.However,without enough time to perform iteration and searching in quick-response situations,they would lose competitiveness compared with some simple quick heuristics based on rules or data.Therefore,it is necessary to hybridize different algorithms so as to address the dual requirements of normal and quick-response ISL schedulings studied in this paper.Note that the normal ISL scheduling over daily BDS management can produce a great number of data (in high-quality if using high-performance metaheuristics),which can be collected to properly perform data-driven quick heuristic in quick-response situations.

With this motivation,this section presents a data-driven heuristic assisted memetic algorithm named DHMA,which hybridizes a high-performance MA and a data-driven heuristic.The main idea of the DHMA is to address normal and quick-response ISL schedulings via the MA and the datadriven heuristic,respectively,while high-quality normal scheduling data are also trained for quick-response use.Following sections will present the framework and details to implement this idea.

A.Framework

The framework of the DHMA to address the dual requirements of normal and quick-response ISL schedulings is shown in Fig.5.Herein,given the inputs from the BDS management agency in normal or quick-response situations,which illustrate the possible ISLs among satellites per timeslot,the scheduling process of the DHMA is separated into the following two aspects:

1)Normal schedulingvia a high-performance MA,as shown in Fig.5(a): In normal situations with certain computing time,better solutions of the ISL scheduling will be searched for as many as possible.A novel high-performance MA that hybridizes parallelism,competition,and evolution strategies will perform this search and output the best-found solution when terminated.Simultaneously,the solution will be stored in a daily solution dataset,which can collect a great number of high-quality ISL scheduling solutions over time.

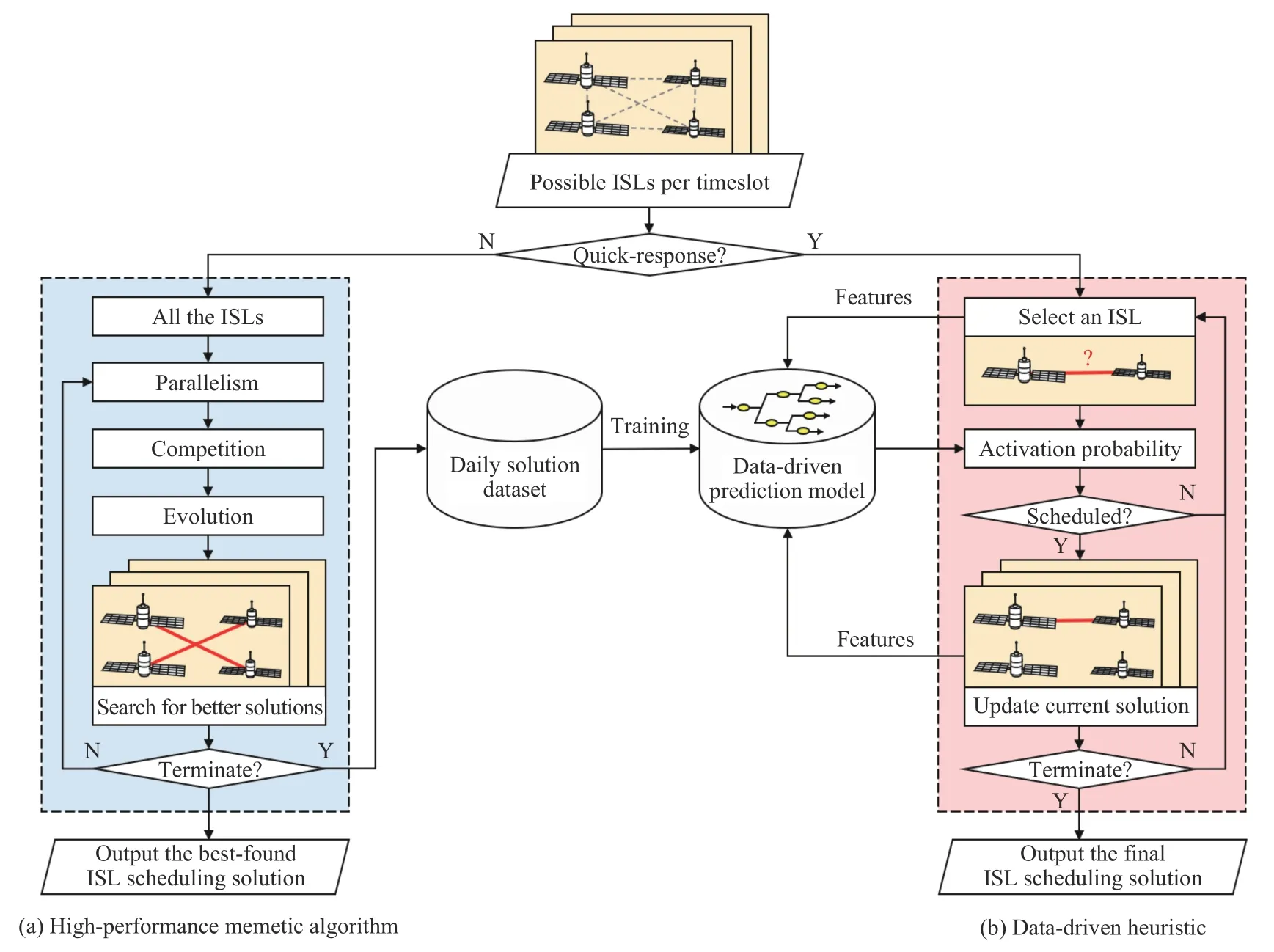
Fig.5.The framework of the DHMA to address the dual requirements of normal and quick-response ISL schedulings.

2)Quick-response schedulingvia a data-driven heuristic,as shown in Fig.5(b):In quick-response situations where only a little computing time is allowed,the ISL scheduling will be addressed by the data-driven heuristic very quickly rather than the aforementioned MA.Herein,given an ISL and current BDS status,a data-driven prediction model trained from the daily solution dataset will predict the probability that this ISL should be activated,assisting in the scheduling decision of this ISL.Thereby in a sequential manner,the heuristic will give priority to high-probability ISLs and quickly output the final solution.

It is worth noticing that all the inputs,including those in normal situations and quick-response situations,are given by the BDS management agency.The algorithm studied in this paper can only serve as an optimizer that optimizes the given inputs from the management agency,with no right or necessity to intervene in how the inputs change.With those aims of normal and quick-response ISL schedulings,the highperformance MA and data-driven heuristic in the DHMA will be further explained in the following two subsections.

B.High-Performance MA

The high-performance MA not only takes charge of highquality ISL scheduling in normal situations,but also supplies high-quality training data required by the data-driven heuristic;hence,its algorithmic design is quite important.With the motivation explained in Section I,a highperformance MA that hybridizes parallelism,competition,and evolution strategies is designed in this subsection,so as to obtain high-quality ISL scheduling solutions in an adaptive and efficient way.

1)Overview

Parallelism,competition,and evolution are three key strategies in this algorithm.As shown in Fig.6,a detailed version of Fig.5(a),the high-performance MA for normal ISL scheduling is implemented by the following steps:

i)Input &initialization:Given the inputs including an algorithm set and an operator set with using probabilities(equal to each other at first),the main thread of the computer will be enabled.Then,an initial population will be randomly generated,where the best individuals will play the initial solutions in the follow-up first-round parallelism strategy.

ii)Inner strategy 1 (Parallelism):In a parallel manner,each thread will run a local search algorithm according to the using probabilities,and the recent-obtained solutions will be recorded.After the local search optimization,those threads will be suspended and then their recent-obtained solutions will be amalgamated into a population set.

iii)Inner strategy 2 (Competition):Local search algorithms and operators will be graded according to the number of solutions they obtained (their contributions)in the population.With these grades,their using probabilities will be updated.In other words,the more solutions an algorithm or operator obtained,the higher it will be graded,and the more frequently it will be used in the next-round parallelism strategy.

iv)Inner strategy 3 (Evolution):With the obtained population,the evolution will be performed so as to explore better solutions.After that,the reproduced solutions will be assigned to different threads and re-play the initial solutions in the next-round parallelism strategy.

Fig.6.The flowchart of the high-performance MA for normal ISL scheduling.

v)Output:When the termination criteria are met,the bestfound solution will be outputted.

Among the three strategies hybridized in this MA:a)The parallelism brings optimization acceleration and diversity.On the one hand,parallel algorithms can certainly perform much more searching within the same running time;on the other hand,those algorithms will obtain diverse solutions in different searching trajectories.b)The competition brings the adaptivity,since the outperforming algorithms and operators will be used more frequently over time,while the underperforming ones will be eliminated.c)The evolution strengthens the exploration ability.It is acknowledged that local search and evolutionary algorithms often outperform in exploitation and exploration,respectively [32]–[35],so the evolution performed after local search optimization will assist in escaping from local optima and explore a larger solution space.With these strategies,this MA is most likely to present overall high performance.Following subsections will implement those strategies in detail.

2)Parallelism

The parallelism is the first strategy per generation.Given an algorithm set and an operator set with using probabilities(equal to each other at first),the parallelism strategy will probabilistically run different local search algorithms with different operators in a parallel manner.After this process,the recent solutions obtained by those algorithms will be outputted.

In algorithm setA,three well-known and widely used local search algorithms,such as Tabu search (TS),simulated annealing (SA),and late acceptance hill-climbing (LA),are included.Also,two hybrid algorithms,such as Tabu simulated annealing (TSA)and Tabu late acceptance hill-climbing(TLA),are included.Herein,only the pseudocodes of the TSA and TLA for the ISL scheduling are given,as shown in Algorithms 1 and 2,respectively.The TS,SA,and LA can be viewed as the simplified variants of the TSA and TLA,so they are no more explained here.

On the basis of the model explained in Fig.3 before,the solution representation of a four-satellite ISL scheduling example is shown in Fig.7.This solution representation matches the decision variables given in Section II-C well.For example,in timeslot 1,ISLsl112andl134are activated so decision variablesx112andx134are thereby set to 1,so are they in timeslots 2 and 3.Note that Fig.7(b)does not encode all the decision variables sincexijkis identically equal toxikjaccording to (1),and self-linking decision variablexijjis automatically assigned in (2).Therefore,Fig.7 builds a clear and brief solution-decision variable relation so that local search operations can be properly performed by modifying decision variables (0 or 1).

Fig.7.The solution representation of a four-satellite ISL scheduling example.(a)Inter-satellite links per timeslot.(b)Decision variable.

With this solution representation,some different local search operators are included in operator setO.By observing the ISLs shown in Fig.7,it can be found easy to perform some changes on them.Herein,five local search operators are designed,including i)ISL change operator that activates a random inactivated ISL or inactivates a random activated one;ii)ISL swap operator that half-swaps the linking satellites of two random activated ISLs within a timeslot;iii)Timeslot swap operator that swaps all the activated ISLs within two random timeslots;iv)Timeslot copy operator that copies all the activated ISLs from a random timeslot to another;and v)Satellite full-linking operator that randomly links all nonlinked visible satellites per timeslot.Note that given a feasible ISL scheduling solution,the last four operators will not violate the major constraints in (1)and (2);hence,those operators are qualified to perform local searching in the ISL scheduling.

These two sets provide available algorithms and operators for optimization,where the using probabilities are initially set equal to each other,and will be adaptively updated by the follow-up competition strategy per generation.In a word,given the available algorithms and operators,the parallelism strategy in this subsection performs parallel local search and outputs a number of optimized solutions.

3)Competition

The competition will be performed among the algorithms and operators after the parallelism strategy so as to update their using probabilities.Specifically,the more solutions an algorithm or operator obtained in the previous parallelism strategy,the higher it will be graded,and the more frequently it will be used in the next-round parallelism.

Assuming that theith algorithm and operator in setsAandOcontributeandsolutions,respectively,to population setSP,their contributionsandwill be graded and updated by (9a)and (9b),respectively.

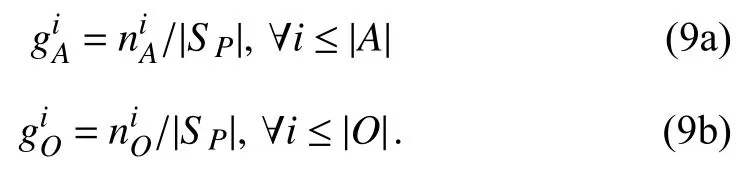
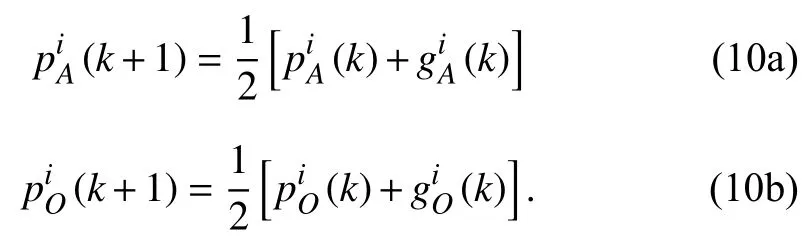
Finally,(11a)and (11b)will normalize the using probabilities of the algorithms and operators,respectively.

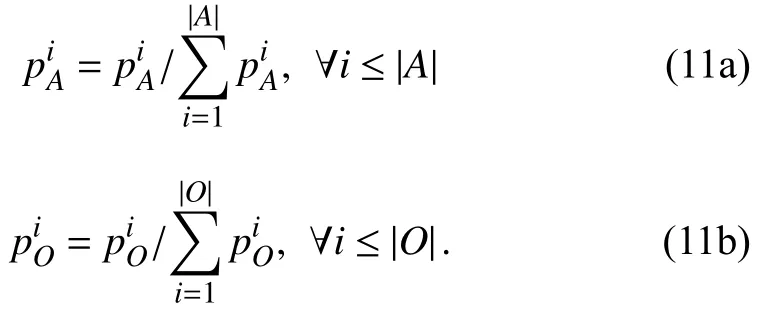
With those normalized probabilities,the roulette will be used when determining which algorithms or operators should be used.Therefore,the competition strategy in this subsection can highlight outperforming algorithms and operators throughout the optimization,contributing to better use of algorithms and operators in an adaptive and efficient manner.

4)Evolution

As the last strategy per generation,the evolution is performed to strengthen the exploration ability that is often lacked in local search optimization.It can also be viewed as the perturbing,destroying,or repair operators in some other local search metaheuristics such as iterative local search (ILS)[36] and adaptive large neighborhood search (ALNS)[37],[38].

Given population setSP,the solutions inSPwill be randomly matched for crossover.Given two matched solutions (parents),namely two series of timeslots with activated ISLs shown in Fig.7,the crossover operator swaps a portion of timeslots of these two solutions,resulting in two new solutions (offsprings).The random one-point crossover is adopted here.Note that the crossover that swaps all the activated ISLs within the same timeslots of two feasible solutions will not violate the major constraints in (1)–(3);hence,the crossover is appropriate for the ISL scheduling.The crossover will be performed according to a pre-set crossover probability,and the best two among the two parents and two offsprings will displace the parents in population setSP.

After all crossover operations in the evolution strategy,the solutions in the new population setSPwill be assigned to the parallel threads to re-play the initial solutions in the nextround parallelism.This assignment will also adopt the roulette with respect to their objective values.In a word,the evolution strategy introduced in this subsection is to perform an explorative search on local-searched solutions,contributing to an escape from local optima for better solutions.

C.Data-Driven Heuristic

The ISL scheduling in the BDS studied in this paper is particular since a great number of ISL scheduling instances must be addressed every day.Although the high-performance MA above can properly obtain high-quality ISL scheduling solutions in normal situations,its searching-based optimization mechanism will certainly spend a lot of time and hardly meet quick-response requirements.Even so,the highquality ISL scheduling solutions from the MA can be collected and thereby trained to assist in quick-response scheduling in a data-driven way.With this motivation,a heuristic that quickly schedules high-probability ISLs according to a data-driven probability prediction model is designed in this subsection.

1)Overview

The main idea of the data-driven heuristic,which is briefly shown in Fig.5(b),is to give priority to high-probability ISLs,where the probabilities are real-time predicted according to a data-driven prediction model trained before.In special,given a satellite and current environment (BDS)status,the highestprobability ISL among all possible and feasible ISLs will be activated.Thereby in a sequential manner,a heuristic can repeatedly perform this process and properly address quickresponse scheduling.To explain the heuristic in detail,its pseudocode is shown in Algorithm 3.

As the pseudocode shows:i)In line 1,the ISLs within later timeslots are considered earlier since the satellite delays within later timeslots should be determined in advance and assist in the prediction within earlier timeslots.ii)From line 3,an empty setPijis used to record the activation probabilities of different ISLs that link thejth satellite within theith timeslot.Then,given ISLlijkand current solutions(where some ISLs have been activated in the BDS),a feature vectorfthat includes certain features with respect to this ISL and current BDS status will be extracted in line 5.Thereby,the prediction model will predict the probability that this ISL should be activated in line 6.iii)After predicting and recording all activation probabilities of different ISLs that link thejth satellite,the probabilities will be sorted in descending order in line 8.With this order,lines 9–16 will activate the highest-probability ISL if it does not violate any constraint.In a word,this heuristic requires each satellite to support the highest-probability ISL under feasible conditions,with the help of a data-driven probability prediction model.

Certainly,the quick-response performance of this heuristic will be affected by the feature extraction and probability prediction in lines 5 and 6,which will be introduced in detail in the next subsection.

2)Prediction Model

Since the probability is predicted with the features from an ISL and current solution,those features should properly reflect the status of the ISL and BDS.Specifically,when considering ISLlijkin the data-driven heuristic,some important features can be obtained and should be used to make the prediction,including:

i)Local features:Given ISLlijk,it can be known that this ISL inter-links satellitessjandskwithin timeslotti;hence,local features with respect to these two satellites should be considered first.The features can be considered in the following aspects:a)Visibility,since the ISL can only be activated between two visible satellites,the visibility should be certainly considered in the decision in the heuristic.b)Inter-linking,since a satellite can only support one ISL per timeslot,whether the satellite has been inter-linked should be considered as well.c)Anchor satellite or not,since the satellite delay can only be reduced by inter-linking anchor satellites,the ISL that inter-links an anchor satellite is much worthy to be activated.d)Delay,since the ISLs within later timeslots are considered earlier in the heuristic,the satellite delays within later timeslotti+1can be calculated in advance,and a high-delay satellite might not be appropriate for data transferring through this ISL.

ii)Global features:In addition to the local features,it is also necessary to observe the whole BDS and consider its global features.Similarly,the features can also be considered in terms of visibility and anchor satellites,but in a global view.For example,given ISLlijkthat inter-links satellitessjandsk,if there are many other anchor satellites visible to satellitesjorsk,this ISL might not be rather required.Also,the activated ISLs should be considered,if there have been many ISLs activated within timeslotti,the activation necessity and probability of the rest ISLs might not be rather high.

According to the feature analysis above,8 local features(IDs 1–8)and 8 global features (IDs 9–16)are selected and will be used for probability prediction in the data-driven heuristic,as shown in Table I.

TABLE I THE FEATURES USED IN THE PREDICTION MODEL IN THE DATADRIvEN HEURISTIC

Among the features in Table I,some are deterministic features that reflect the facts in the BDS given timeslotti,including features 1,2,3,4,9,10,11,12,13,and 14.Besides,other features,including features 5,6,7,8,15,and 16,depend on different combinations of activated ISLs and need to be updated once an ISL is activated throughout the heuristic process.Admittedly,those feature updates would spend time in certain degrees.To further demonstrate that the designed data-driven heuristic can quickly address the ISL scheduling in quick-response situations,the heuristic complexity is analyzed in the next subsection.

3)Complexity Analysis

Since the data-driven heuristic in this section is designed for quick-response ISL scheduling,where only a little computing time is allowed,it is necessary to analyze its time complexity.The time complexity of this data-driven heuristic results from the superposition of three aspects,including:

i)Heuristic complexity:By observing the heuristic loops in lines 1,2,4,and 8 in Algorithm 3,it can be easily deduced that the complexity is,namelyO(n2).

ii)Feature extraction complexity:The feature extraction complexity should also be separately analyzed in terms of local and global features.On the one hand,all the local features (IDs 1–8)in Table I are self-considered and will be calculated only once,resulting in the same complexity ofO(1).On the other hand,the global features (IDs 9–16)in Table I can be determined by looping all the satellites in the BDS,resulting in the complexity ofO(n).Therefore,the complexity that extracts all the features in Table I should beO(n).

iii)Prediction complexity:Since the probability prediction in line 6 in Algorithm 3 can be viewed as an additional function,which will not be affected by the problem size,the prediction complexity here isO(1).

As Algorithm 3 shows,the feature extraction and prediction are performed per step in lines 5 and 6 in the heuristic,so the total time complexity of the designed data-driven heuristic will beO(n3),which is polynomial.In other words,the datadriven heuristic can complete the ISL scheduling in polynomial time,which will properly meet the requirements in quick-response scheduling situations.

4)Model Training

Before applying the designed data-driven heuristic in quickresponse ISL scheduling situations,the prediction model that predicts ISL activation probabilities in line 6 in Algorithm 3 needs training.The training data just come from the highquality ISL scheduling solutions in the daily solution dataset,which are obtained by the aforementioned high-performance MA in Section III-B in normal situations.

In this paper,the model training will be performed via the eXtreme Gradient Boosting (XGBoost)algorithm [39],which is a well-designed gradient-boosted decision tree algorithm that has demonstrated its advantages in many state-of-the-art studies [40]–[43].The XGBoost belongs to the widely used tree-learning algorithms that do not require linear features or linear interactions among features,where a decision tree makes predictions according to a series of rules arranged in a tree-like structure.To prevent model overfitting and probably validate the model,the five-fold cross-validation will be performed to obtain the best model parameters during the model training.Note that the model training algorithm is not the focus of this study compared with the data-driven idea in quick-response scheduling,so other outperforming algorithms are no more discussed or used in the paper.

Above all,this section introduces the details of the proposed DHMA,where a high-performance MA and a data-driven heuristic are special for addressing normal and quick-response ISL schedulings,respectively.In the next section,an experimental study will be conducted to examine the proposed DHMA and show its performance in real-world applications.

IV.EXpERIMENTAL STUDY

In this section,the experiment setup is given first.Then,the seven-day ISL scheduling results via the proposed DHMA are presented in both normal and quick-response situations.Furthermore,the statistical performance and parameter sensitivity of the DHMA are also analyzed.

A.Experiment Setup

The new-generation BDS (BDS-3),which was completely constructed on June 23,2020,was selected to examine the DHMA proposed in this paper.The BDS includes 24 medium earth orbit (MEO)satellites,3 geostationary orbit (GEO)satellites,and 3 inclined geosynchronous orbit (IGSO)satellites.The Beijing Station (center ground station)was included,so the satellites that are visible to Beijing Station were anchor satellites per timeslot,per superframe.The experimental orbit parameters of the BDS are shown in Table II[4].A seven-day experiment was conducted,in which the seven days were divided into totally 10 080 superframes(instances,in minutes),and each superframe was further divided into 20 timeslots (in 3 seconds),just as [4],[10],and[11] did in common.The seven-day dataset will serve as the inputs in both normal situation and quick-response situation,so the normal and quick-response scheduling results via the DHMA can be clearly compared.

The DHMA was implemented by Java 1.8.0,while the data training was implemented by Scikit-learn [44] in Python 3.6,using an Intel (R)Core (TM)i7-7600U CPU at 2.80 GHz under Windows 10 with 8 GB RAM and 4 threads.In the normal situation,the high-performance MA in the DHMA was performed.It adopts the SA,LA,TSA,and TLA in its parallelism strategy,where the sizes of the Tabu solution set and the late solution set were set to 10 and 50,respectively,and the anneal coefficient was set to 0.95.The crossover probability in the evolution strategy was set to 70%.The evolution strategy in the MA was performed every 6 seconds,and the MA did not terminate until running for 30 seconds per superframe.All the ISL scheduling results obtained by the MA from the 10 080 superframes were stored in the daily solution dataset and thereby regarded as the training data for the data-driven heuristic in the DHMA.

In the quick-response situation,the data-driven heuristic in the DHMA was performed,where a PMML-formatted prediction model trained by the XGBoost algorithm was preloaded.The parameters of the XGBoost include estimators(300),Max.tree depth (7),learning rate (0.03),Min.child weight (3),subsample (0.7),and gamma (0.2).Also,a small random disturbing coefficient (0.02)was performed on the prediction results.

B.Experimental Results

The seven-day ISL scheduling results including 10 080 superframes (instances)via the proposed DHMA are summarized in Table III,where the high-performance MA and the data-driven heuristic were performed in normal and quickresponse situations,respectively.Note that Table III shows the results in terms of Max.,Ave.,and Min.delays and different ISL numbers in a superframe,among which only the Ave.delay (marked by 1)is the objective modeled in Section III-C.Also,the Max.,Ave.,and Min.values of them among the 10 080 superframes are also calculated.In this way,Table III provides an overall view of the ISL scheduling effects in the BDS over seven days,in both normal and quick-response situations.

In the normal situation,the high-performance MA in the DHMA can reduce the Max.delay per superframe to 4,3.02,and 2 timeslots (at least,on average,and at most,respectively),and also reduce the Ave.delay per superframe to 1.62,1.16,and 1.03 timeslots,respectively.The Min.delay equals 1 all the time since there are always some non-anchor satellites in the BDS.As a result,it can be summarized that the DHMA can normally reduce the BDS delay to 4 timeslots at least and to 1.16 timeslots on average,as many as 12 seconds and 3.48 seconds,respectively.Simultaneously,it can be summarized from the ISL number results that each satellite in the BDS can support 8 different ISLs at least and 12.49 different ISLs on average per superframe.Those results are shown more intuitively in Fig.8,where the results show periodical tendencies due to the periodical satellite positions in the BDS over the seven days.Note that there are only 0.1%4-timeslot delays and 1.7% 3-timeslot delays shown in Fig.8(b),and the most (84.7%)delays are 1 timeslot.Those results satisfy all the constraints and can meet the requirements of the BDS management agency.Herein,the computing time of the MA was 30 seconds per superframe,so the seven-day scheduling with 10 080 superframes took up to 84 hours in total.

When it comes to the quick-response situation in Table III,the data-driven heuristic in the DHMA can reduce the Max.delay per superframe to 7,4.62,and 2 timeslots (at least,on average,and at most,respectively),and also reduce the Ave.delay per superframe to 2.20,1.30,and 1.05 timeslots,respectively.As a result,it can be summarized that the DHMA in the quick-response situation can reduce the BDS delay to 7 timeslots at least and to 1.30 timeslots on average,as many as 21 seconds and 3.90 seconds,respectively.Simultaneously,it can also be summarized that each satellite in the BDS can support 6 different ISLs at least and 11.17 different ISLs on average per superframe.Those results are shown more intuitively in Fig.9,where the results show similar tendencies to Fig.8.Admittedly,the quick-response heuristic results here cannot outperform the normal MA results above,but it can still show good competitiveness given such little computing time.Under such circumstances,most(77.6%)of the delays are also 1 timeslot,and only 1.6%delays are over 3 timeslots.Moreover,note that the Ave.computing time herein was only 0.22 seconds per superframe,so the seven-day scheduling with 10 080 superframes took only 37 minutes.

By comparing the DHMA performance in normal and quick-response situations above,it can be considered that the seven-day ISL scheduling computing time is considerablyreduced from 84 hours to only 37 minutes in the quickresponse situation,while the quick-response results still show good competitiveness.This is exactly what the BDS management agency requires.

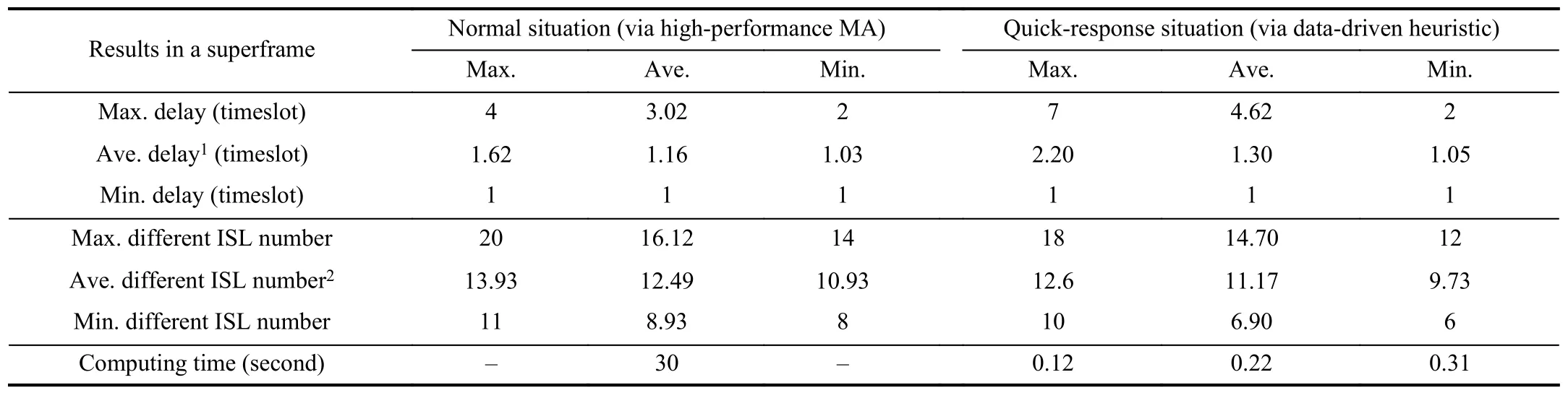
TABLE III OvERvIEw RESULTS OF THE SEvEN-DAY ISL NORMAL AND QUICk-RESpONSE SCHEDULINGS IN THE BDS VIA THE DHMA

Fig.8.Seven-day ISL scheduling results in the normal situation via the high-performance MA.(a)The delay and different ISL numbers per superframe.(b)Full-time percentages of different delays and ISL numbers.(c)The heat map of the Ave.delay per satellite per superframe.(d)The heat map of the different ISLs supported per satellite per superframe.

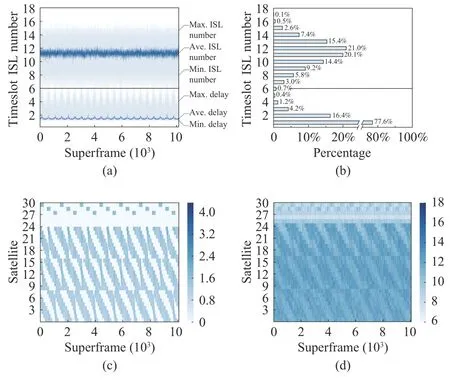
Fig.9.Seven-day ISL scheduling results in the quick-response situation via the data-driven heuristic.(a)The delay and different ISL numbers per superframe.(b)Full-time percentages of different delays and ISL numbers.(c)The heat map of the Ave.delay per satellite per superframe.(d)The heat map of the different ISLs supported per satellite per superframe.

In summary,the experiment results above examine the efficient performance of the proposed DHMA in both normal and quick-response situations.In the normal situation,the high-performance MA in the DHMA can properly address the ISL scheduling and thereby offer a great number of highquality data.In the quick-response situation,the data-driven heuristic competitively addresses the ISL scheduling as well,spending only a little computing time.

C.Comparison Analysis

In addition,to show the statistical performance of the proposed DHMA compared with other commonly used algorithms,further comparison experiments were also conducted.The competitors in the comparison experiments include:

Metaheuristic Competitors in the Normal Situation:Since the used high-performance MA in the DHMA is designed with additional parallelism,competition,and evolution strategies,some related metaheuristics were employed as competitors.They are i)a single TSA,and ii)TLA hybridized in the parallelism strategy in the high-performance MA,iii)a well-known genetic algorithm (GA),and iv)an unparallel MA that only uses TSA (TSA-MA),and v)that only uses TLA(TLA-MA).

Heuristic Competitors in the Quick-Response Situation:Since the data-driven heuristic in the DHMA is performed in the quick-response situation,some other quick heuristics with less or no data assistance were employed as competitors.They are i)a data-driven heuristic with local features only,ii)a data-driven heuristic with global features only,iii)a random heuristic that sequentially activates random ISLs,and iv)a commonly used first-fit heuristic in satellite imaging scheduling,which sequentially activates the first feasible ISLs.

1)Normal Scheduling

In the normal situation,Ave.50-run ISL scheduling results in terms of delays and different ISL numbers are shown in Tables IV and V,respectively,where the first superframes every day were selected in the experiments.

TABLE IV AvE.50-RUN ISL SCHEDULING RESULTS (OF DELAYS) COMpARISON IN THE NORMAL SITUATION

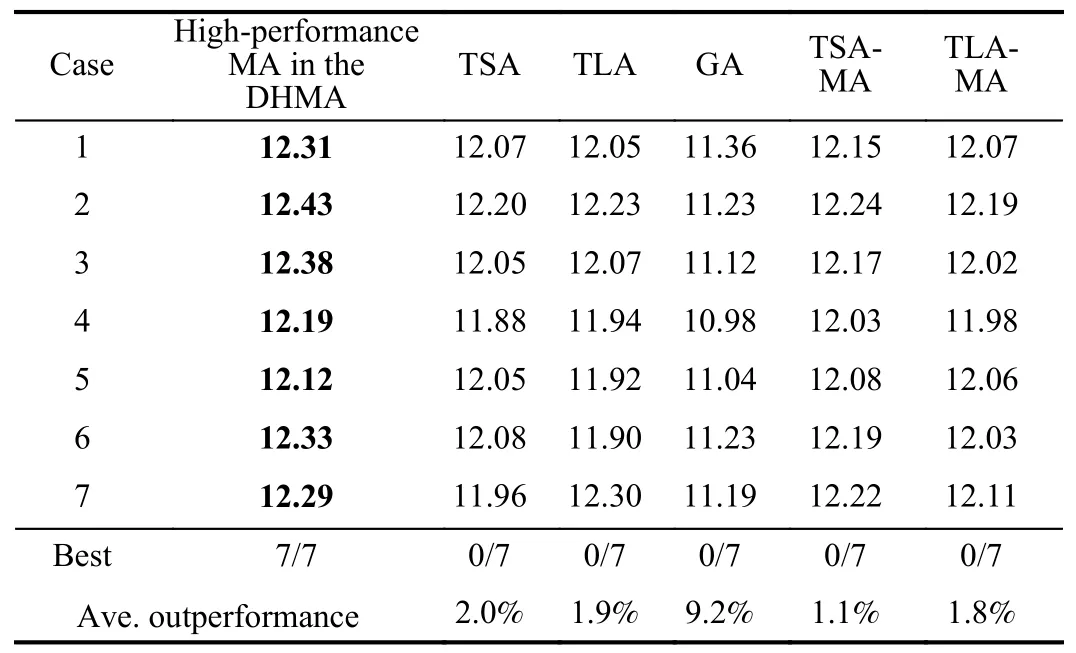
TABLE V AvE.50-RUN ISL SCHEDULING RESULTS (OF DIFFERENT ISL NUMBERS) COMpARISON IN THE NORMAL SITUATION

It can be observed in Table IV that the high-performance MA in the proposed DHMA obtains 6 best Ave.results(lowest delays)among 7 cases,outperforming other competitors by 0.7% to 8.9%.In Table V,it obtains all best Ave.results (largest numbers of different ISLs)and outperforms by 1.1% to 9.2%.These results show that given the same computing time,the proposed DHMA is competitive in normal ISL scheduling via the high-performance MA,which hybridizes more strategies and performs searching more adaptively and efficiently.In addition,it can be observed that local search-led algorithms,including the DHMA,TSA,TLA,TSA-MA,and TLA-MA,outperform the evolution-led GA.This phenomenon meets the conclusion in[11],which would be due to the fact that local search operators could perform more efficient searching than crossover operators in the ISL scheduling problem with strict constraints.

To show how the parallelism and competition strategies work in the high-performance MA,the using probabilities of algorithms and operators per generation in Case 1 in Table IV are illustrated in Fig.10.In Fig.10(a),the using probabilities of the four parallel algorithms including the SA,LA,TSA,and TLA were set to 0.25 at first but differ a lot as the generation increases,since their using probabilities were modified according to their performance over time.Herein,the TSA (marked in gray)often performed well,while the LA(marked in red)often underperformed but still made some contributions.Also note that,although some algorithms cannot show full-time good performance,they can still assist in exploring solutions and increasing solution diversity in this MA.A similar phenomenon can be observed in Fig.10(b),where using probabilities of the five operators defined in Section III-B also show different tendencies.In this way,the parallelism and competition strategies in this MA properly highlight the outperforming algorithms and operators and thereby promote efficient optimization.

Fig.10.An illustration of the using probabilities of algorithms and operators per generation throughout the high-performance MA in the DHMA.(a)The probabilities of algorithms.(b)The probabilities of operators.

2)Quick-Response Scheduling

When it comes to the quick-response situation,Ave.50-run ISL scheduling results in terms of delays and different ISL numbers are shown in Tables VI and VII,respectively.In Table VI,it can be observed that the data-driven heuristic in the proposed DHMA obtains all best Ave.results (shortest delays)among the 7 cases,outperforming other competitors by 3.3% at least.These results also indicate that the datadriven heuristic should overall consider local and global features since it cannot properly work if only with local or global features.Also,note that although the first-fit heuristic is widely used in satellite imaging scheduling and other realworld optimization problems,it shows extremely poor performance in the ISL scheduling studied in this paper.The poor performance should be attributed to that the first-fit heuristic blindly gives priority to similar ISLs within different timeslots in the sequential manner,but actually the ISL diversity is required so that the system delay can be thereby reduced.This also explains that even the random heuristic shows not-bad performance.

Conversely in Table VII,the random heuristic obtains all best Ave.results (largest numbers of different ISLs),while the data-driven heuristic in the proposed DHMA underperformsby 2.4%.This phenomenon is also reasonable since the randomness often determines the diversity,so the random heuristic is more likely to result in more diverse and different ISLs among satellites.However,the randomness cannot guarantee the performance,the random heuristic underperforms in the results of delays mentioned above.Considering other competitors,the data-driven heuristic in the DHMA still outperforms,while the firs-fit heuristic still shows poor performance.According to these results,the data-driven heuristic certainly turns into a good choice for the ISL scheduling in the quick-response situation.

TABLE VI AvE.50-RUN ISL SCHEDULING RESULTS (OF DELAYS) COMpARISON IN THE QUICk-RESpONSE SITUATION

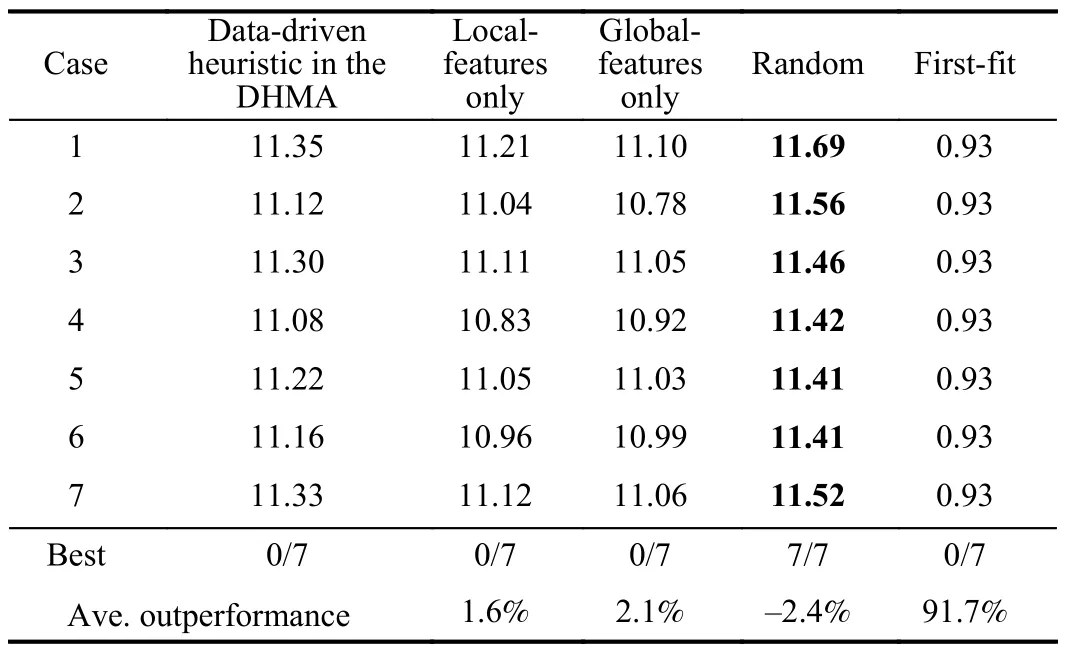
TABLE VII AvE.50-RUN ISL SCHEDULING RESULTS (OF DIFFERENT ISL NUMBERS) COMpARISON IN THE QUICk-RESpONSE SITUATION

In summary,the comparison experiment results above further examine the DHMA performance in both normal and quick-response situations.As a result,the DHMA can show good competitiveness to address the studied ISL scheduling by reducing the system delays and activating more different ISLs.

D.Parameter Analysis

Several major parameters in the high-performance MA and data-driven heuristic in the DHMA were chosen for an orthogonal array experiment to show the parameter sensitivity.As shown in Table VIII,these parameters are divided into three levels,and the Ave.50-run ISL scheduling results in anL9(34)-based orthogonal array experiment [45] are shown in Table IX.Herein,the delays and different ISL numbers are both involved and will be analyzed.

TABLE VIII PARAMETER LEvELS IN THE DHMA FOR THE ORTHOGONAL ARRAY EXpERIMENT

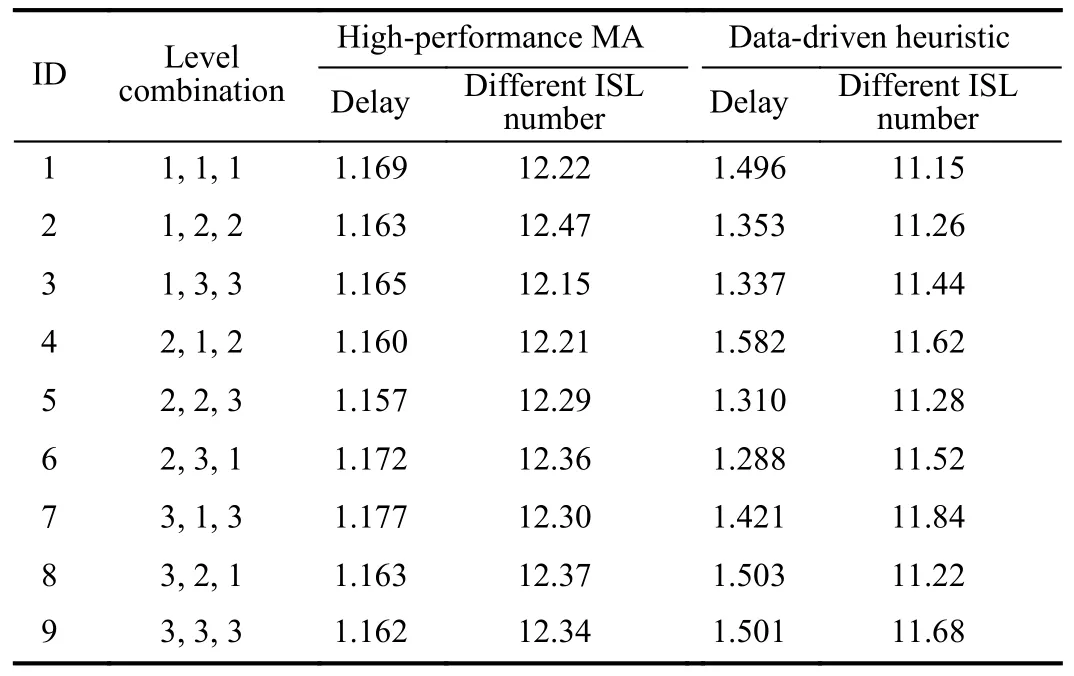
TABLE IX AvE.50-RUN ISL SCHEDULING RESULTS VIA THE DHMA IN THE ORTHOGONAL ARRAY EXpERIMENT

Table X shows the Ave.response values and ranks of the parameters.On the one hand,the high-performance MA achieves the shortest Ave.delays (marked in bold)when its Tabu size,late size,and anneal coefficient were set to Levels 2 (10),2 (50),and 2 (0.95),respectively.On the other hand,the data-driven heuristic achieves the shortest Ave.delays when its Max.tree depth,learning rate,and Min.child weight were set to Levels 2 (7),3 (0.03),and 3 (3),respectively.These results match the parameter setting in previous experiments.Also,it can be observed that the highperformance MA shows very low Delta values,which indicate its insensitivity to the parameters and strong robustness.Among those parameters,the late size and learning rate have major impacts on the high-performance MA and data-driven heuristic,respectively.

When it comes to the results in terms of different ISL numbers,Table XI shows a similar version.On the one hand,the high-performance MA achieves the largest Ave.different ISL numbers (marked in bold)when its Tabu size,late size,and anneal coefficient were set to Levels 3 (20),2 (50),and 2(0.95),respectively.On the other hand,the data-driven heuristic achieves the largest Ave.different ISL numbers when its Max.tree depth,learning rate,and Min.child weight were set to Levels 3 (10),3 (0.03),and 2 or 3 (2 or 3),respectively.Among those parameters,the late size and Max.tree depth have major impacts on the high-performance MAand data-driven heuristic,respectively.

TABLE X AvE.RESpONSE VALUES AND RANkS OF PARAMETERS (IN TERMS OF DELAYS)

TABLE XI AvE.RESpONSE VALUES AND RANkS OF PARAMETERS (IN TERMS OF DIFFERENT ISL NUMBERS)

Above all,it can be summarized that Levels 2 and 3 are the suggested parameter levels in the DHMA for the ISL scheduling studied in this paper,where the late size,learning rate,and Max.tree depth have great impacts.

V.DISCUSSIONS

With the experimental results above,the highlights and practicability of the proposed DHMA are discussed in this section.First of all,the DHMA is designed for real-world applications,where high-quality scheduling and quickresponse scheduling are often contradicted.In most cases,high-quality scheduling requires some computing time,which is certainly lacked in quick-response situations.Nonetheless,the DHMA proposed in this paper catches a potential connection between them,that is the high-quality scheduling can thereby offer high-quality data and assist in the quick response in a data-driven manner.In this regard,a highperformance MA and a data-driven heuristic are included in the DHMA for addressing normal and quick-response ISL schedulings,respectively.Despite the fact that only a sevenday experiment was conducted in this paper,it shows the possibility that the MA can supply high-quality training data and support the quick heuristic in the data-driven manner for real-world applications.

The second highlight of the DHMA is its great applicability to the ISL scheduling problem in the BDS studied in this paper,since the BDS can produce a considerable number of real-world data every day.Currently,the ISL scheduling in the BDS is performed every one-minute superframe,so 10 080 instances of real-world data can be collected over sevenday BDS management.Regarding other problems such as satellite imaging scheduling,which is often performed once a day,only 7 instances of real-world data can be collected over seven-day management.Therefore,the ISL scheduling studied in this paper offers greater data potential,so the proposed DHMA is more appliable and can perform better.

Also,the DHMA is an expandable (evolvable)algorithm that can be updated (upgraded)over time.On the one hand,its high-performance MA that parallelly and adaptatively runs different algorithms can absorb other new outperforming algorithms,only by throwing them into the algorithm set and enabling new threads.On the other hand,its prediction model in the data-driven heuristic can be cumulatively trained with the long-term high-quality data,as well as the latest data.In comparison with some highly parameter-dependent or environment-dependent algorithms,the proposed DHMA can show greater competitiveness.

Last but not least,the proposed DHMA is easy to understand and implement,where no complicated algorithm or strategy is designed.Therefore,the DHMA is friendly to the researchers and practitioners in the BDS management agency for real-world use.

VI.CONCLUSIONS

To address the dual requirements of normal and quickresponse ISL schedulings in real-world BDS applications,this paper proposes a data-driven heuristic assisted memetic algorithm named DHMA,which includes a high-performance MA and a data-driven heuristic for normal and quick-response schedulings,respectively.The main idea of the DHMA is to address normal and quick-response schedulings separately,while high-quality normal scheduling data are also trained for quick-response use.A seven-day experiment including 10 080 instances well examines the efficient performance of the proposed DHMA.

In addition to the DHMA,the contributions of this paper also include the easy-to-understand ISL scheduling modeling.The DHMA with this model can be applied to other real-world satellite systems,such as the ISL-based communication satellite networks.Future work will include long-term experiments with more history datasets and interactions,also,more outperforming algorithms will be transplanted and engineered in new open-access DHMAs for real-world use.